Тройной сюжет

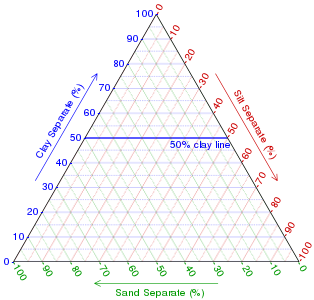
Троичный график , троичный график , треугольный график , симплексный график или треугольник Гиббса — это барицентрический график трех переменных, сумма которых равна константе. ^[1] Он графически изображает отношения трех переменных в виде позиций в равностороннем треугольнике . Он используется в физической химии , петрологии , минералогии , металлургии и других физических науках, чтобы показать состав систем, состоящих из трех видов. Троичные графики — это инструменты для анализа композиционных данных в трехмерном случае.

В популяционной генетике треугольный график частот генотипов называется диаграммой де Финетти . В теории игр ^[2] и выпуклая оптимизация , ^[3] его часто называют симплексным сюжетом.

На троичном графике значения трех переменных $a$ , $b$ и $c$ суммироваться с некоторой константой $K.$ должны Обычно эту константу представляют как 1,0 или 100%. Поскольку $a + b + c = K$ для всех веществ, отображаемых на графике, ни одна переменная не является независимой от других, поэтому необходимо знать только две переменные, чтобы найти точку образца на графике: например, $c$ должна быть равна $K — а - б$ . Поскольку три числовых значения не могут изменяться независимо (есть только две степени свободы ), можно изобразить комбинации всех трех переменных только в двух измерениях.

Преимущество использования троичного графика для изображения химического состава заключается в том, что три переменные можно удобно отобразить на двумерном графике. Троичные графики также можно использовать для создания фазовых диаграмм путем выделения на графике областей состава, где существуют разные фазы.

Значения точки на троичном графике соответствуют (с точностью до константы) ее трилинейным координатам или барицентрическим координатам .

Чтение значений на троичном графике

Существует три эквивалентных метода, которые можно использовать для определения значений точки на графике:

параллельных линий или Метод сетки . Первый метод — использовать сетку диаграммы, состоящую из линий, параллельных ребрам треугольника. Параллелью стороне треугольника называется геометрическое место точек, постоянных в компоненте, расположенной в вершине, противоположной стороне. Каждая составляющая составляет 100% в углу треугольника и 0% на противоположном ему ребре, убывая линейно с увеличением расстояния (перпендикулярно противоположному краю) от этого угла. Рисуя параллельные линии через равные промежутки между нулевой линией и углом, можно установить тонкие деления для облегчения оценки.
перпендикулярных линий или Метод высот . Для диаграмм, на которых нет линий сетки, самый простой способ определить значения — определить кратчайшие (т. е. перпендикулярные) расстояния от интересующей точки до каждой из трех сторон. По теореме Вивиани расстояния (или отношения расстояний к высоте треугольника ) дают значение каждого компонента.
угловой линии или Метод пересечения . Третий метод не требует рисования перпендикулярных или параллельных линий. Прямые линии проводятся от каждого угла через интересующую точку к противоположной стороне треугольника. Длины этих линий, а также длины отрезков между точкой и соответствующими сторонами измеряются индивидуально. Тогда соотношение измеренных линий дает значение компонента в виде доли 100%.

Смещение вдоль параллельной линии (линии сетки) сохраняет сумму двух значений, тогда как движение вдоль перпендикулярной линии увеличивает (или уменьшает) два значения на равную величину, каждое на половину уменьшения (увеличения) третьего значения. Движение вдоль линии через угол сохраняет соотношение двух других значений.

Рисунок 1. Высотный метод
Рисунок 2. Метод пересечения
Рисунок 3. Пример троичной диаграммы без нанесенных точек.
Рисунок 4. Пример троичной диаграммы, показывающий приращения вдоль первой оси.
Рисунок 5. Пример троичной диаграммы, показывающий приращение вдоль второй оси.
Рисунок 6. Пример троичной диаграммы, показывающий приращения по третьей оси.
Рисунок 7. Пустой троичный график
Рисунок 8. Индикация работы трех осей.
Немаркированный треугольный график с основными линиями сетки
Немаркированный треугольный график с основными и второстепенными линиями сетки

Вывод из декартовых координат

На рисунке (1) показана наклонная проекция точки $P(a, b, c)$ в трёхмерном декартовом пространстве с осями $a$ , $b$ и $c$ соответственно.

Если $a + b + c = K$ (положительная константа), $P$ ограничивается плоскостью, содержащей $A(K,0,0)$ , $B(0, K,0)$ и $C(0,0, K)$ . Если $a$ , $b$ и $c$ не могут быть отрицательными, $P$ ограничивается треугольником, ограниченным $A$ , $B$ и $C$ , как в (2).

В (3) оси повернуты для получения изометрического вида. Треугольник, если смотреть лицом вниз, кажется равносторонним .

В (4) расстояния $P$ от линий $BC$ , $AC$ и $AB$ обозначены $a'$ , $b'$ и $c'$ соответственно.

Для любой прямой $l = s + t n̂$ в векторной форме ( $n̂$ — единичный вектор) и точки $p$ расстояние по перпендикуляру от $p$ до $l$ равно

\left\|(\mathbf {s} -\mathbf {p} )-{\bigl (}(\mathbf {s} -\mathbf {p} )\cdot \mathbf {\hat {n}} {\bigr )}\mathbf {\hat {n}} \right\|\,.

В этом случае точка $P$ находится в

\mathbf {p} ={\begin{pmatrix}a\\b\\c\end{pmatrix}}\,.

Линия $BC$ имеет

\mathbf {s} ={\begin{pmatrix}0\\K\\0\end{pmatrix}}\quad {\text{and}}\quad \mathbf {\hat {n}} ={\frac {{\begin{pmatrix}0\\K\\0\end{pmatrix}}-{\begin{pmatrix}0\\0\\K\end{pmatrix}}}{\left\|{\begin{pmatrix}0\\K\\0\end{pmatrix}}-{\begin{pmatrix}0\\0\\K\end{pmatrix}}\right\|}}={\frac {\begin{pmatrix}0\\K\\-K\end{pmatrix}}{\sqrt {0^{2}+K^{2}+{(-K)}^{2}}}}={\begin{pmatrix}0\\{\frac {1}{\sqrt {2}}}\\-{\frac {1}{\sqrt {2}}}\end{pmatrix}}\,.

Используя формулу перпендикулярного расстояния,

{\begin{aligned}a'&=\left\|{\begin{pmatrix}-a\\K-b\\-c\end{pmatrix}}-\left({\begin{pmatrix}-a\\K-b\\-c\end{pmatrix}}\cdot {\begin{pmatrix}0\\{\frac {1}{\sqrt {2}}}\\-{\frac {1}{\sqrt {2}}}\end{pmatrix}}\right){\begin{pmatrix}0\\{\frac {1}{\sqrt {2}}}\\-{\frac {1}{\sqrt {2}}}\end{pmatrix}}\right\|\\[10px]&=\left\|{\begin{pmatrix}-a\\K-b\\-c\end{pmatrix}}-\left(0+{\frac {K-b}{\sqrt {2}}}+{\frac {c}{\sqrt {2}}}\right){\begin{pmatrix}0\\{\frac {1}{\sqrt {2}}}\\-{\frac {1}{\sqrt {2}}}\end{pmatrix}}\right\|\\[10px]&=\left\|{\begin{pmatrix}-a\\K-b-{\frac {K-b+c}{2}}\\-c+{\frac {K-b+c}{2}}\end{pmatrix}}\right\|=\left\|{\begin{pmatrix}-a\\{\frac {K-b-c}{2}}\\{\frac {K-b-c}{2}}\end{pmatrix}}\right\|\\[10px]&={\sqrt {{(-a)}^{2}+{\left({\frac {K-b-c}{2}}\right)}^{2}+{\left({\frac {K-b-c}{2}}\right)}^{2}}}={\sqrt {a^{2}+{\frac {{(K-b-c)}^{2}}{2}}}}\,.\end{aligned}}

Подставляя $K = a + b + c$ ,

a'={\sqrt {a^{2}+{\frac {{(a+b+c-b-c)}^{2}}{2}}}}={\sqrt {a^{2}+{\frac {a^{2}}{2}}}}=a{\sqrt {\frac {3}{2}}}\,.

Аналогичный расчет по линиям $AC$ и $AB$ дает

b'=b{\sqrt {\frac {3}{2}}}\quad {\text{and}}\quad c'=c{\sqrt {\frac {3}{2}}}\,.

Это показывает, что расстояние точки от соответствующих линий линейно пропорционально исходным значениям $a$ , $b$ и $c$ . ^[4]

Построение троичного графика

Декартовы координаты полезны для построения точек в треугольнике. Рассмотрим равносторонний троичный график, где $a = 100%$ расположено в $(x, y) = (0,0)$ и $b = 100%$ в $(1,0)$ . Тогда $c = 100$ % ${\textstyle ({\frac {1}{2}},{\frac {\sqrt {3}}{2}}),}$ а тройка $(a, b, c)$ есть

\left({\frac {1}{2}}\cdot {\frac {2b+c}{a+b+c}},{\frac {\sqrt {3}}{2}}\cdot {\frac {c}{a+b+c}}\right)\,.

Пример

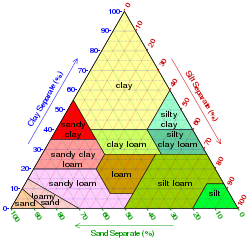
В этом примере показано, как это работает для гипотетического набора из трех образцов почвы:

Образец	Глина	Ил	Песок	Примечания
Образец 1	50%	20%	30%	Поскольку глина и ил вместе составляют 70% этого образца, доля песка должна составлять 30%, чтобы сумма компонентов составляла 100%.
Образец 2	10%	60%	30%	Доля песка составляет 30%, как и в образце 1, но при увеличении доли ила на 40% доля глины соответственно уменьшается.
Образец 3	10%	30%	60%	Этот образец содержит ту же долю глины, что и образец 2, но пропорции ила и песка поменяны местами; график отражается вокруг своей вертикальной оси.

Нанесение точек

Построение графика образца 1 (шаг 1):
Найдите линию 50% глины.
Построение графика образца 1 (шаг 2):
Найдите линию с содержанием ила 20%.
Построение графика образца 1 (шаг 3):
Будучи зависимым от первых двух, пересечение находится на линии песка 30%.
Построение графиков всех образцов
Тройной треугольный график типов почвы, песка, глины и ила, запрограммированный с помощью Mathematica

Список известных троичных диаграмм

Диаграмма цветности
диаграмма де Финетти
Сюжет Далица
Диаграмма воспламеняемости
Катионный график Дженсена
Диаграмма Пайпера , используемая в гидрохимии.
Классификационная диаграмма UIGS для ультраосновных пород
Министерства сельского хозяйства США Диаграмма текстуры почвы по размерам частиц

См. также

Ссылки

^ Вайсштейн, Эрик В. «Трнарная диаграмма» . mathworld.wolfram.com . Проверено 5 июня 2021 г.
^ Карл Тейлс, «Эволюционный теоретико-игровой анализ покерных стратегий», Entertainment Computing, январь 2009 г. doi : 10.1016/j.entcom.2009.09.002 , с. 9
^ Бойд С. и Ванденбергхе Л., 2004. Выпуклая оптимизация. Издательство Кембриджского университета.
^ Воан, Уилл (5 сентября 2010 г.). «Тройные сюжеты» . Архивировано из оригинала 20 декабря 2010 года . Проверено 7 сентября 2010 г.

Внешние ссылки

«Шаблон Excel для троичных диаграмм» . serc.carleton.edu . Ресурсный центр научно-образовательного образования (SERC) Карлтон-колледжа . Проверено 14 мая 2020 г.
«Tri-plot: программное обеспечение для построения троичных диаграмм» . www.lboro.ac.uk . Университет Лафборо – Факультет географии / Портал ресурсов домой > Три сюжета . Проверено 14 мая 2020 г.
«Генератор троичных диаграмм – быстро создавайте троичные диаграммы в режиме онлайн» . www.ternaryplot.com . Проверено 14 мая 2020 г.
Холланд, Стивен (2016). «Анализ данных в науках о Земле – троичные диаграммы, разработанные на языке R» . Strata.uga.edu . Университет Джорджии . Проверено 14 мая 2020 г.

[1] Вайсштейн, Эрик В. «Трнарная диаграмма» . mathworld.wolfram.com . Проверено 5 июня 2021 г.

[2] Карл Тейлс, «Эволюционный теоретико-игровой анализ покерных стратегий», Entertainment Computing, январь 2009 г. doi : 10.1016/j.entcom.2009.09.002 , с. 9

[3] Бойд С. и Ванденбергхе Л., 2004. Выпуклая оптимизация. Издательство Кембриджского университета.

[Vaughan-4] Воан, Уилл (5 сентября 2010 г.). «Тройные сюжеты» . Архивировано из оригинала 20 декабря 2010 года . Проверено 7 сентября 2010 г.

[1]

[2]

[3]

[4]

v т и Химические растворы
Решение	Идеальное решение Водный раствор Твердый раствор Буферный раствор Флори-Хаггинс Смесь Приостановка Коллоид Фазовая диаграмма Разделение фаз Эвтектическая точка Сплав Насыщенность Пересыщение Серийное разбавление Разбавление (уравнение) Очевидные молярные свойства Разрыв смешиваемости
Концентрация и соответствующие количества	Молярная концентрация Массовая концентрация Числовая концентрация Объемная концентрация Нормальность Моляльность Мольная доля Массовая доля Изотопное изобилие Соотношение смешивания Тройной сюжет
Растворимость	Равновесие растворимости Общее количество растворенных твердых веществ сольватация Сольватная оболочка Энтальпия раствора Решетчатая энергия Закон Рауля Закон Генри Таблица растворимости (данные) Таблица растворимости Смешиваемость
Растворитель	( Категория ) Константа диссоциации кислоты Протонный растворитель Полярный апротонный растворитель Неорганический неводный растворитель сольватация Список информации о кипячении и замерзании растворителей Коэффициент распределения Полярность гидрофобный гидрофильный Липофильный Амфифил Лионий ион Лиат-ион