ВПГМА

WPGMA ( взвешенной группы пар метод метод Сокалу арифметическим со средним это простой агломеративный (восходящий) иерархической кластеризации , обычно приписываемый ) — и Миченеру . ^[1]

Метод WPGMA аналогичен своему невзвешенному варианту — методу UPGMA .

Алгоритм

Алгоритм WPGMA строит корневое дерево ( дендрограмму ), которое отражает структуру, присутствующую в матрице попарных расстояний (или матрице подобия ). На каждом шаге ближайшие два кластера, скажем $i$ и $j$ , объединяются в кластер более высокого уровня $i\cup j$ . Тогда его расстояние до другого кластера $k$ это просто среднее арифметическое средних расстояний между членами $k$ и $i$ и $k$ и $j$ :

$d_{(i\cup j),k}={\frac {d_{i,k}+d_{j,k}}{2}}$

Алгоритм WPGMA создает корневые дендрограммы и требует предположения о постоянной скорости: он создает ультраметрическое дерево, в котором расстояния от корня до каждой вершины ветвей равны. Это предположение об ультраметричности называется молекулярными часами , когда кончики включают ДНК , РНК и белка данные .

Рабочий пример

Этот рабочий пример основан на JC69 матрице генетических расстояний , рассчитанной на основе выравнивания последовательностей 5S рибосомальной РНК пяти бактерий: Bacillus subtilis ( $a$ ), Bacillus stearothermophilus ( $b$ ), Lactobacillus viridescens ( $c$ ), Ахолеплазма хоть ( $d$ ) и Micrococcus luteus ( $e$ ). ^[2]^[3]

Первый шаг

Первая кластеризация

Предположим, что у нас есть пять элементов $(a,b,c,d,e)$ и следующая матрица $D_{1}$ попарных расстояний между ними:

	а	б	с	д	и
а	0	17	21	31	23
б	17	0	30	34	21
с	21	30	0	28	39
д	31	34	28	0	43
и	23	21	39	43	0

В этом примере $D_{1}(a,b)=17$ это наименьшее значение $D_{1}$ , поэтому мы соединяем элементы $a$ и $b$ .

Оценка длины первой ветки

Позволять $u$ обозначаем узел, к которому $a$ и $b$ теперь подключены. Параметр $\delta (a,u)=\delta (b,u)=D_{1}(a,b)/2$ гарантирует, что элементы $a$ и $b$ равноудалены от $u$ . Это соответствует ожиданию гипотезы ультраметричности .Ветви, соединяющиеся $a$ и $b$ к $u$ тогда есть длины $\delta (a,u)=\delta (b,u)=17/2=8.5$ ( см. окончательную дендрограмму )

Первое обновление матрицы расстояний

Затем мы приступаем к обновлению исходной матрицы расстояний. $D_{1}$ в новую матрицу расстояний $D_{2}$ (см. ниже), уменьшенный в размере на одну строку и один столбец из-за кластеризации $a$ с $b$ .Жирные значения в $D_{2}$ соответствуют новым расстояниям, рассчитанным путем усреднения расстояний между каждым элементом первого кластера $(a,b)$ и каждый из оставшихся элементов:

$D_{2}((a,b),c)=(D_{1}(a,c)+D_{1}(b,c))/2=(21+30)/2=25.5$

$D_{2}((a,b),d)=(D_{1}(a,d)+D_{1}(b,d))/2=(31+34)/2=32.5$

$D_{2}((a,b),e)=(D_{1}(a,e)+D_{1}(b,e))/2=(23+21)/2=22$

Значения, выделенные курсивом $D_{2}$ на них не влияет обновление матрицы, поскольку они соответствуют расстояниям между элементами, не участвующими в первом кластере.

Второй шаг

Вторая кластеризация

Теперь мы повторяем три предыдущих шага, начиная с новой матрицы расстояний. $D_{2}$ :

	(а, б)	с	д	и
(а, б)	0	25.5	32.5	22
с	25.5	0	28	39
д	32.5	28	0	43
и	22	39	43	0

Здесь, $D_{2}((a,b),e)=22$ это наименьшее значение $D_{2}$ , поэтому мы присоединяемся к кластеру $(a,b)$ и элемент $e$ .

Оценка длины второй ветви

Позволять $v$ обозначаем узел, к которому $(a,b)$ и $e$ теперь подключены. Из-за ограничения ультраметричности ветви, соединяющиеся $a$ или $b$ к $v$ , и $e$ к $v$ равны и имеют следующую длину: $\delta (a,v)=\delta (b,v)=\delta (e,v)=22/2=11$

Выводим недостающую длину ветки: $\delta (u,v)=\delta (e,v)-\delta (a,u)=\delta (e,v)-\delta (b,u)=11-8.5=2.5$ ( см. окончательную дендрограмму )

Обновление матрицы второго расстояния

Затем мы приступаем к обновлению $D_{2}$ матрицу в новую матрицу расстояний $D_{3}$ (см. ниже), уменьшенный в размере на одну строку и один столбец из-за кластеризации $(a,b)$ с $e$ : $D_{3}(((a,b),e),c)=(D_{2}((a,b),c)+D_{2}(e,c))/2=(25.5+39)/2=32.25$

Следует отметить, что этот средний расчет нового расстояния не учитывает больший размер $(a,b)$ кластер (два элемента) по отношению к $e$ (один элемент). Сходным образом:

$D_{3}(((a,b),e),d)=(D_{2}((a,b),d)+D_{2}(e,d))/2=(32.5+43)/2=37.75$

Таким образом, процедура усреднения придает дифференциальный вес начальным расстояниям матрицы $D_{1}$ . По этой причине метод взвешивается не по отношению к математической процедуре, а по отношению к начальным расстояниям.

Третий шаг

Третья кластеризация

Мы снова повторяем три предыдущих шага, начиная с обновленной матрицы расстояний. $D_{3}$ .

	((а,б),д)	с	д
((а,б),д)	0	32.25	37.75
с	32.25	0	28
д	37.75	28	0

Здесь, $D_{3}(c,d)=28$ это наименьшее значение $D_{3}$ , поэтому мы соединяем элементы $c$ и $d$ .

Оценка длины третьей ветви

Позволять $w$ обозначаем узел, к которому $c$ и $d$ теперь подключены.Ветви, соединяющиеся $c$ и $d$ к $w$ тогда есть длины $\delta (c,w)=\delta (d,w)=28/2=14$ ( см. окончательную дендрограмму )

Обновление матрицы третьего расстояния

Есть одна запись для обновления: $D_{4}((c,d),((a,b),e))=(D_{3}(c,((a,b),e))+D_{3}(d,((a,b),e)))/2=(32.25+37.75)/2=35$

Последний шаг

Финал $D_{4}$ матрица:

	((а,б),д)	(в, г)
((а,б),д)	0	35
(в, г)	35	0

Итак, мы объединяем кластеры $((a,b),e)$ и $(c,d)$ .

Позволять $r$ обозначают (корневой) узел, к которому $((a,b),e)$ и $(c,d)$ теперь подключены.Ветви, соединяющиеся $((a,b),e)$ и $(c,d)$ к $r$ тогда имейте длину:

$\delta (((a,b),e),r)=\delta ((c,d),r)=35/2=17.5$

Выводим две оставшиеся длины ветвей:

$\delta (v,r)=\delta (((a,b),e),r)-\delta (e,v)=17.5-11=6.5$

$\delta (w,r)=\delta ((c,d),r)-\delta (c,w)=17.5-14=3.5$

Дендрограмма WPGMA

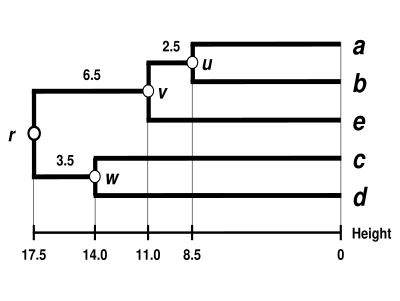
Дендрограмма готова. Он ультраметрический, потому что все кончики ( $a$ к $e$ ) равноудалены от $r$ :

$\delta (a,r)=\delta (b,r)=\delta (e,r)=\delta (c,r)=\delta (d,r)=17.5$

Таким образом, дендрограмма имеет корни $r$ , его самый глубокий узел.

Сравнение с другими связями

Альтернативные схемы связей включают кластеризацию с одной связью , кластеризацию с полной связью и кластеризацию со средней связью UPGMA . Реализация другой связи — это просто вопрос использования другой формулы для расчета расстояний между кластерами на этапах обновления матрицы расстояний вышеуказанного алгоритма. Полная кластеризация позволяет избежать недостатка альтернативного метода кластеризации с одной связью — так называемого явления цепочки , при котором кластеры, сформированные с помощью кластеризации с одной связью, могут быть объединены вместе из-за того, что отдельные элементы находятся близко друг к другу, даже если многие элементы в каждом из них кластеры могут находиться очень далеко друг от друга. Полная связь имеет тенденцию находить компактные кластеры примерно одинакового диаметра. ^[4]

Сравнение дендрограмм, полученных разными методами кластеризации из одной и той же матрицы расстояний .

Кластеризация с одной связью	Кластеризация с полной связью	Кластеризация средних связей: WPGMA.	Кластеризация средней связи: UPGMA

См. также

Ссылки

^ Сокаль , Миченер (1958). «Статистический метод оценки систематических связей» . Научный бюллетень Канзасского университета . 38 : 1409–1438.
^ Эрдманн В.А., Уолтерс Дж. (1986). «Коллекция опубликованных последовательностей рибосомальных РНК 5S, 5,8S и 4,5S» . Исследования нуклеиновых кислот . 14 Дополнение (Suppl): r1–59. дои : 10.1093/nar/14.suppl.r1 . ПМК 341310 . ПМИД 2422630 .
^ Олсен Дж.Дж. (1988). «Филогенетический анализ с использованием рибосомальной РНК». Рибосомы . Методы энзимологии. Том. 164. стр. 793–812. дои : 10.1016/s0076-6879(88)64084-5 . ISBN 978-0-12-182065-7 . ПМИД 3241556 .
^ Эверитт, бакалавр наук; Ландау, С.; Лиз, М. (2001). Кластерный анализ. 4-е издание . Лондон: Арнольд. стр. 62–64.

[1] Сокаль , Миченер (1958). «Статистический метод оценки систематических связей» . Научный бюллетень Канзасского университета . 38 : 1409–1438.

[Erdmann1986-2] Эрдманн В.А., Уолтерс Дж. (1986). «Коллекция опубликованных последовательностей рибосомальных РНК 5S, 5,8S и 4,5S» . Исследования нуклеиновых кислот . 14 Дополнение (Suppl): r1–59. дои : 10.1093/nar/14.suppl.r1 . ПМК 341310 . ПМИД 2422630 .

[Olsen1988-3] Олсен Дж.Дж. (1988). «Филогенетический анализ с использованием рибосомальной РНК». Рибосомы . Методы энзимологии. Том. 164. стр. 793–812. дои : 10.1016/s0076-6879(88)64084-5 . ISBN 978-0-12-182065-7 . ПМИД 3241556 .

[4] Эверитт, бакалавр наук; Ландау, С.; Лиз, М. (2001). Кластерный анализ. 4-е издание . Лондон: Арнольд. стр. 62–64.

[1]

[2]

[3]

[4]

v т и Филогенетика
Соответствующие поля	Вычислительная филогенетика Молекулярная филогенетика кладистика Таксономия Эволюционная таксономия Систематика	Портал эволюционной биологии
Основные понятия	Филогенез Кладогенез Филогенетическое дерево Кладограмма Филогенетическая сеть Аттракцион «Длинная ветка» Клэйд против Грейда Родословная Родословная призрака Население призраков
Методы вывода	Максимальная экономия Филогенетическое примирение Вероятностные методы Максимальная вероятность Байесовский вывод Дистанционно-матричные методы Присоединение к соседям УПГМА Наименьшие квадраты Трех-таксонный анализ
Текущие темы	Филокод ДНК-штрихкодирование Молекулярная филогенетика Филогенетические сравнительные методы Консерватизм филогенетической ниши Филогенетический сигнал Программное обеспечение для филогенетики Филогеномика Филогеография
Групповые черты	Примитивный Плезиоморфия Симплезиоморфия Полученный Апоморфия Синапоморфия Аутапоморфия
Типы групп	монофилия Парафилия Полифилия
Номенклатура	Филогенетическая номенклатура Коронная группа Сестринская группа Базальный Супердерево
Категория Коммонс