Диск (математика)

«2-шар» перенаправляется сюда. Чтобы узнать о баскетбольном мероприятии, см. 2Ball .

Чтобы узнать о других целях, см. Диск .

Диск с

  окружность С

  диаметр D

  радиус R

  центр или начало координат O

В геометрии диск . ( также пишется диск ) — это область на плоскости, ограниченная кругом . Диск называется замкнутым , если он содержит окружность, образующую его границу, и открытым , если его нет.

Для радиуса, $r$, открытый диск обычно обозначается как $D_{r}$ и закрытый диск ${\overline {D_{r}}}$. Однако в области топологии закрытый диск обычно обозначается как $D^{2}$ пока открытый диск $\operatorname {Int} D^{2}$.

Формулы

В декартовых координатах открытый диск центра $(a,b)$ а радиус R определяется по формуле:

$D=\{(x,y)\in {\mathbb {R} ^{2}}:(x-a)^{2}+(y-b)^{2}<R^{2}\}$

в то время как закрытый диск с тем же центром и радиусом определяется выражением:

${\overline {D}}=\{(x,y)\in {\mathbb {R} ^{2}}:(x-a)^{2}+(y-b)^{2}\leq R^{2}\}.$

Площадь равна закрытого или открытого диска радиуса R π R. ² (см. область диска ).

Характеристики

Диск имеет круговую симметрию .

Открытый диск и закрытый диск топологически не эквивалентны (то есть не гомеоморфны ), так как обладают топологическими свойствами, отличными друг от друга. Например, каждый закрытый диск компактен , тогда как каждый открытый диск не компактен. Однако с точки зрения алгебраической топологии у них много общих свойств: оба они стягиваемы. и поэтому гомотопически эквивалентны одной точке. Отсюда следует, что их фундаментальные группы тривиальны, а все группы гомологий тривиальны, кроме 0-й, изоморфной Z . Эйлерова характеристика точки (а значит, и замкнутого или открытого диска) равна 1.

Каждое непрерывное отображение замкнутого диска в себя имеет хотя бы одну неподвижную точку (мы не требуем, чтобы отображение было биективным или даже сюръективным ); это случай n = 2 теоремы Брауэра о неподвижной точке . Утверждение неверно для открытого диска:

Рассмотрим, например, функцию $f(x,y)=\left({\frac {x+{\sqrt {1-y^{2}}}}{2}},y\right)$который отображает каждую точку открытого единичного диска в другую точку открытого единичного диска справа от данной. Но для замкнутого единичного диска он фиксирует каждую точку полукруга. $x^{2}+y^{2}=1,x>0.$

Как статистическое распределение

Среднее расстояние до локации от точек на диске

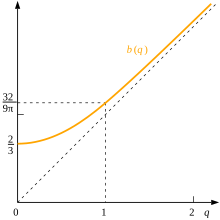
В статистике иногда встречается равномерное распределение на единичном круговом диске. Чаще всего это происходит при исследовании операций в области математики городского планирования, где его можно использовать для моделирования населения города. В других целях можно воспользоваться тем фактом, что это распределение, для которого легко вычислить вероятность того, что заданный набор линейных неравенств будет удовлетворен. ( Гауссово распределение на плоскости требует числовой квадратуры .)

«Гениальный аргумент с помощью элементарных функций» показывает, что среднее евклидово расстояние между двумя точками диска равно ⁠ 128 / 45π ⁠ ≈ 0.90541 , в то время как прямое интегрирование в полярных координатах показывает, что среднеквадратичное расстояние равно 1 .

Если нам дано произвольное местоположение на расстоянии q от центра диска, то также представляет интерес определить среднее расстояние b ( q ) от точек распределения до этого местоположения и средний квадрат таких расстояний. Последнее значение можно вычислить непосредственно как q ² + ⁠ 1 / 2 ⁠ .

Среднее расстояние до произвольной внутренней точки

Среднее расстояние от диска до внутренней точки

Чтобы найти b ( q ), нам нужно отдельно рассмотреть случаи, когда местоположение является внутренним или внешним, т.е. когда q ≶ 1 , и мы обнаруживаем, что в обоих случаях результат может быть выражен только через полные эллиптические интегралы .

Если мы рассматриваем внутреннее местоположение, наша цель (глядя на диаграмму) состоит в том, чтобы вычислить ожидаемое значение r при распределении, плотность которого равна ⁠ 1 / π ⁠ для 0 ≤ r ≤ s (θ) , интегрирование в полярных координатах с центром в фиксированном месте, для которого площадь ячейки равна r d r dθ ; следовательно $$b(q)={\frac {1}{\pi }}\int _{0}^{2\pi }{\textrm {d}}\theta \int _{0}^{s(\theta )}r^{2}{\textrm {d}}r={\frac {1}{3\pi }}\int _{0}^{2\pi }s(\theta )^{3}{\textrm {d}}\theta .$$

Здесь s (θ) можно найти через q и θ, используя закон косинусов . Шаги, необходимые для вычисления интеграла, а также несколько ссылок можно найти в статье Лью и др.; результат таков, что $$b(q)={\frac {4}{9\pi }}{\biggl \{}4(q^{2}-1)K(q^{2})+(q^{2}+7)E(q^{2}){\biggr \}}$$где K и E — полные эллиптические интегралы первого и второго рода. б (0) = ⁠ 2/3 ​ ⁠ ; ​ б (1) = ⁠ 32 / 9π ⁠ ≈ 1.13177 .

Среднее расстояние до произвольной внешней точки

Среднее расстояние от диска до внешней точки

Обращаясь к внешнему расположению, мы можем аналогичным образом настроить интеграл, на этот раз получив

$$b(q)={\frac {2}{3\pi }}\int _{0}^{{\textrm {sin}}^{-1}{\tfrac {1}{q}}}{\biggl \{}s_{+}(\theta )^{3}-s_{-}(\theta )^{3}{\biggr \}}{\textrm {d}}\theta$$где закон косинусов говорит нам, что s ₊ (θ) и s _– (θ) являются корнями для s уравнения $$s^{2}-2qs\,{\textrm {cos}}\theta +q^{2}\!-\!1=0.$$Следовательно $$b(q)={\frac {4}{3\pi }}\int _{0}^{{\textrm {sin}}^{-1}{\tfrac {1}{q}}}{\biggl \{}3q^{2}{\textrm {cos}}^{2}\theta {\sqrt {1-q^{2}{\textrm {sin}}^{2}\theta }}+{\Bigl (}1-q^{2}{\textrm {sin}}^{2}\theta {\Bigr )}^{\tfrac {3}{2}}{\biggl \}}{\textrm {d}}\theta .$$Мы можем заменить u = q sinθ, чтобы получить $${\begin{aligned}b(q)&={\frac {4}{3\pi }}\int _{0}^{1}{\biggl \{}3{\sqrt {q^{2}-u^{2}}}{\sqrt {1-u^{2}}}+{\frac {(1-u^{2})^{\tfrac {3}{2}}}{\sqrt {q^{2}-u^{2}}}}{\biggr \}}{\textrm {d}}u\\[0.6ex]&={\frac {4}{3\pi }}\int _{0}^{1}{\biggl \{}4{\sqrt {q^{2}-u^{2}}}{\sqrt {1-u^{2}}}-{\frac {q^{2}-1}{q}}{\frac {\sqrt {1-u^{2}}}{\sqrt {q^{2}-u^{2}}}}{\biggr \}}{\textrm {d}}u\\[0.6ex]&={\frac {4}{3\pi }}{\biggl \{}{\frac {4q}{3}}{\biggl (}(q^{2}+1)E({\tfrac {1}{q^{2}}})-(q^{2}-1)K({\tfrac {1}{q^{2}}}){\biggr )}-(q^{2}-1){\biggl (}qE({\tfrac {1}{q^{2}}})-{\frac {q^{2}-1}{q}}K({\tfrac {1}{q^{2}}}){\biggr )}{\biggr \}}\\[0.6ex]&={\frac {4}{9\pi }}{\biggl \{}q(q^{2}+7)E({\tfrac {1}{q^{2}}})-{\frac {q^{2}-1}{q}}(q^{2}+3)K({\tfrac {1}{q^{2}}}){\biggr \}}\end{aligned}}$$используя стандартные интегралы.

Следовательно, снова b (1) = ⁠ 32 / 9π ⁠ , а также $$\lim _{q\to \infty }b(q)=q+{\tfrac {1}{8q}}.$$

См. также

• Единичный диск , диск радиуса один
• Кольцо (математика) , область между двумя концентрическими кругами.
• Шар (математика) — обычный термин для обозначения трёхмерного аналога диска.
• Дисковая алгебра , пространство функций на диске.
• Круглый сегмент
• Ортоцентроидальный диск , содержащий определенные центры треугольника.