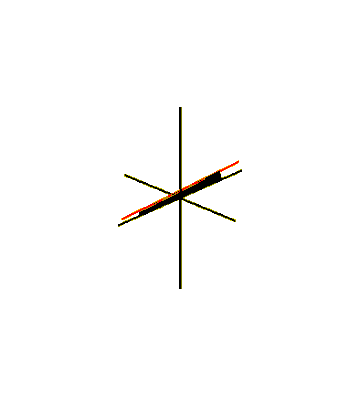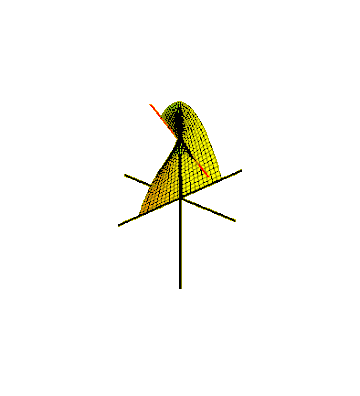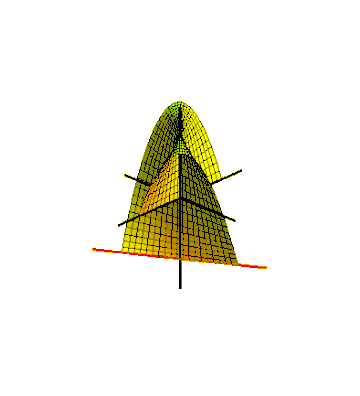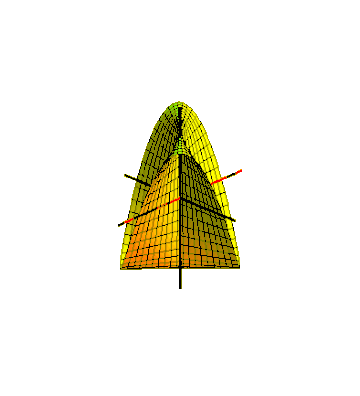Лента Мёбиуса

Лента Мёбиуса из бумаги и скотча.

В математике — лента Мёбиуса , лента Мёбиуса или петля Мёбиуса. поверхность , которую можно сформировать, соединив концы полоски бумаги полуповоротом. Как математический объект он был обнаружен Иоганном Бенедиктом Листингом и Августом Фердинандом Мёбиусом в 1858 году, но уже появлялся в римских мозаиках третьего века нашей эры . Лента Мёбиуса представляет собой неориентируемую поверхность, а это означает, что внутри нее нельзя последовательно отличить повороты по часовой стрелке от поворотов против часовой стрелки. Каждая неориентируемая поверхность содержит полосу Мёбиуса.

Как абстрактное топологическое пространство , лента Мёбиуса может быть вложена в трехмерное евклидово пространство разными способами: полуповорот по часовой стрелке отличается от полуповорота против часовой стрелки, а также может быть вложен с нечетным числом витков, превышающим один, или с узловатой средней линией. Любые два вложения с одинаковым узлом на центральной линии и одинаковым числом и направлением витков топологически эквивалентны . Все эти вложения имеют только одну сторону, но при вложении в другие пространства лента Мёбиуса может иметь две стороны. Он имеет только одну граничную кривую .

Несколько геометрических конструкций ленты Мёбиуса придают ей дополнительную структуру. По ней можно перемещаться как по линейчатой ​​поверхности отрезком линии, вращающимся во вращающейся плоскости, с самопересечениями или без них. Тонкая бумажная полоска, концы которой соединены в ленту Мёбиуса, может плавно сгибаться в виде развертывающейся поверхности или складываться плоско ; уплощенные ленты Мёбиуса включают тригексафлексагон . Суданская лента Мёбиуса — минимальная поверхность в гиперсфере , а лента Микса Мёбиуса — самопересекающаяся минимальная поверхность в обычном евклидовом пространстве. И суданская лента Мёбиуса, и другая самопересекающаяся лента Мёбиуса, перекрестная граница, имеют круглую границу. Лента Мёбиуса без края, называемая открытой лентой Мёбиуса, может образовывать поверхности постоянной кривизны . Некоторые высокосимметричные пространства, точки которых представляют собой прямые на плоскости, имеют форму ленты Мёбиуса.

Ленты Мёбиуса применяются во многих сферах, включая механические ремни , которые изнашиваются равномерно с обеих сторон, двухпутные американские горки , каретки которых чередуются между двумя дорожками, а также карты мира, напечатанные так, что антиподы появляются друг напротив друга. Ленты Мёбиуса появляются в молекулах и устройствах с новыми электрическими и электромеханическими свойствами и используются для доказательства результатов невозможности в теории социального выбора . В массовой культуре ленты Мёбиуса появляются в произведениях Эшера , Макса Билла и других, а также в дизайне символа переработки . Многие архитектурные концепции были вдохновлены лентой Мёбиуса, в том числе проект здания Зала славы NASCAR . Исполнители, в том числе Гарри Блэкстоун-старший и Томас Нельсон Даунс, основывали сценические фокусы на свойствах ленты Мёбиуса. каноны С помощью лент Мёбиуса И.С. Баха проанализированы . Во многих произведениях спекулятивной фантастики используются ленты Мёбиуса; В более общем смысле, в художественной литературе распространена структура сюжета, основанная на ленте Мёбиуса, где события повторяются с неожиданными поворотами.

История

Мозаика из древнего Сентинума, изображающая Айона, держащего ленту Мёбиуса.

Цепной насос с приводной цепью Мёбиуса работы Исмаила аль-Джазари (1206 г.)

Открытие ленты Мёбиуса как математического объекта независимо приписывается немецким математикам Иоганну Бенедикту Листингу и Августу Фердинанду Мёбиусу в 1858 году. Однако он был известен задолго до этого и как физический объект, и в художественных изображениях; в частности, его можно увидеть на нескольких римских мозаиках третьего века нашей эры. Во многих случаях они просто изображают скрученные ленты в качестве границ. При нечетном числе витков эти ленты представляют собой ленты Мёбиуса, но при четном числе витков они топологически эквивалентны раскрученным кольцам . Таким образом, то, является ли лента лентой Мёбиуса, может быть случайным, а не осознанным выбором. По крайней мере, в одном случае лента с разными цветами на разных сторонах была нарисована с нечетным количеством витков, что вынудило художника неуклюже исправить место, где цвета не совпадали. Другая мозаика из города Сентинум (изображена) изображает зодиак , принадлежащий богу Айону , в виде ленты с одним поворотом. Нет явных доказательств того, что односторонность этого визуального представления небесного времени была преднамеренной; его можно было выбрать просто как способ заставить все знаки зодиака появиться на видимой стороне полосы. Некоторые другие древние изображения уробуро или украшений в форме восьмерки также предположительно изображают ленты Мёбиуса, но неясно, предназначались ли они для изображения плоских полос любого типа .

Независимо от математической традиции машиностроителям давно известно, что механические ремни изнашиваются вдвое быстрее, чем ленты Мёбиуса, поскольку они используют всю поверхность ремня, а не только внутреннюю поверхность нескрученного ремня. Кроме того, такой ремень может быть менее склонен к скручиванию из стороны в сторону. Раннее письменное описание этой техники датируется 1871 годом, то есть после первых математических публикаций, посвященных ленте Мёбиуса. Намного раньше изображение цепного насоса в работе Исмаила аль-Джазари 1206 года изображает конфигурацию ленты Мёбиуса для его приводной цепи. Еще одно использование этой поверхности было сделано швеями в Париже (в неустановленную дату): они инициировали новичков, требуя от них пришить ленту Мёбиуса в качестве воротника к одежде.

Свойства

2D-объект, пройдя один раз вокруг ленты Мёбиуса, возвращается в зеркальной форме.

Лента Мёбиуса обладает несколькими любопытными свойствами. Это неориентируемая поверхность : если асимметричный двумерный объект скользит один раз по полосе, он возвращается в исходное положение как свое зеркальное отражение. В частности, изогнутая стрелка, указывающая по часовой стрелке (↻), вернется в виде стрелки, указывающей против часовой стрелки (↺), подразумевая, что в пределах ленты Мёбиуса невозможно последовательно определить, что значит быть по часовой стрелке или против часовой стрелки. Это простейшая неориентируемая поверхность: любая другая поверхность неориентируема тогда и только тогда, когда она имеет в качестве подмножества ленту Мёбиуса. Соответственно, будучи вставленной в евклидово пространство , лента Мёбиуса имеет только одну сторону. Трехмерный объект, который скользит один раз по поверхности полосы, не отражается, а вместо этого возвращается в ту же точку полосы, что локально кажется ее другой стороной, показывая, что обе позиции на самом деле являются частью одной стороны. . Такое поведение отличается от привычных ориентируемых поверхностей в трех измерениях, например, моделируемых плоскими листами бумаги, цилиндрическими соломинками для питья или полыми шариками, у которых одна сторона поверхности не соединена с другой. Однако это свойство ее вложения в пространство, а не внутреннее свойство самой ленты Мёбиуса: существуют другие топологические пространства, в которые ленту Мёбиуса можно вложить так, чтобы она имела две стороны. Например, если переднюю и заднюю грани куба склеить друг с другом с зеркальным отражением влево-вправо, в результате получится трехмерное топологическое пространство ( декартово произведение ленты Мёбиуса с интервалом), в котором вершина а нижние половины куба можно отделить друг от друга двусторонней лентой Мёбиуса. В отличие от дисков, сфер и цилиндров, для которых можно одновременно вложить несчетное множество непересекающихся копий в трехмерное пространство , одновременно можно вложить только счетное число лент Мёбиуса.

Путь вдоль края ленты Мёбиуса, прослеживаемый до тех пор, пока он не вернется в исходную точку на краю, включает все граничные точки ленты Мёбиуса в одну непрерывную кривую. Лента Мёбиуса, полученная путем склеивания и скручивания прямоугольника, имеет длину в два раза больше средней линии ленты. В этом смысле лента Мёбиуса отличается от раскрученного кольца и, подобно круговому диску, тем, что имеет только одну границу. Ленту Мёбиуса в евклидовом пространстве нельзя переместить или растянуть до зеркального отображения; это киральный объект с праворукостью или леворукостью. Ленты Мёбиуса с нечетным числом полуповоротов, превышающих единицу, или завязанные перед склейкой, отличаются как вложенные подмножества трехмерного пространства, хотя все они эквивалентны как двумерные топологические поверхности. Точнее, две ленты Мёбиуса эквивалентно вложены в трехмерное пространство, если их центральные линии определяют один и тот же узел и имеют одинаковое количество витков, что и друг друга. Однако при четном числе витков получается другая топологическая поверхность, называемая кольцом .

Ленту Мёбиуса можно плавно трансформировать в ее осевую линию, делая ее уже и фиксируя точки на осевой линии. Это преобразование является примером ретракции деформации , и его существование означает, что лента Мёбиуса обладает многими из тех же свойств, что и ее центральная линия, которая топологически представляет собой круг. В частности, его фундаментальная группа такая же, как фундаментальная группа круга, бесконечная циклическая группа . Следовательно, пути на ленте Мёбиуса, которые начинаются и заканчиваются в одной и той же точке, можно топологически отличить (с точностью до гомотопии ) только по количеству раз, когда они обходят ленту.

При разрезании центральной линии получается двусторонняя (не Мёбиуса) полоса двойной длины.

В результате одиночного разреза со смещением от центра получается лента Мёбиуса (фиолетовая), соединенная с двусторонней полосой двойной длины.

Разрезание ленты Мёбиуса по центральной линии ножницами дает одну длинную полосу с четырьмя полуповоротами (относительно раскрученного кольца или цилиндра), а не две отдельные полосы. Два полуповорота возникают из-за того, что эта более тонкая полоска дважды проходит через полуповорот в исходной ленте Мёбиуса, а два других возникают из-за того, что две половинки более тонкой полосы оборачиваются друг вокруг друга. В результате получается не лента Мёбиуса, а топологически эквивалентный цилиндру. Разрезав эту полосу двойной скрутки еще раз вдоль ее центральной линии, получим две соединенные полосы двойной скрутки. Если вместо этого разрезать ленту Мёбиуса вдоль на треть ширины, получится две связанные ленты. Один из двух представляет собой центральную, более тонкую ленту Мёбиуса, а другой имеет два полуповорота. Эти взаимосвязанные формы, образованные продольными срезами лент Мёбиуса различной ширины, иногда называют парадромными кольцами .

Подразделение на шесть смежных областей, ограниченных графом Титце.

Решение задачи трех полезностей на ленте Мёбиуса

Ленту Мёбиуса можно разрезать на шесть смежных областей, показывая, что карты на поверхности ленты Мёбиуса иногда могут требовать шести цветов, в отличие от теоремы о четырёх цветах для плоскости. Шести цветов всегда достаточно. Этот результат является частью теоремы Рингеля-Янгса , которая утверждает, сколько цветов нужно каждой топологической поверхности. Ребра и вершины этих шести областей образуют граф Титце , который является двойственным графом с шестью вершинами на этой поверхности для полного графа , но не может быть нарисован без пересечений на плоскости . Другое семейство графов, которые можно вложить в ленту Мёбиуса, но не в плоскость, — это лестницы Мёбиуса , границы подразделений ленты Мёбиуса на прямоугольники, пересекающиеся из конца в конец. с шестью вершинами К ним относится граф полезности, полный двудольный граф , вложение которого в ленту Мёбиуса показывает, что, в отличие от плоскости, задача трёх полезностей может быть решена на прозрачной ленте Мёбиуса. Эйлерова характеристика ленты Мёбиуса равна нулю , что означает, что при любом подразделении ленты вершинами и ребрами на области числа $V$, $E$, и $F$ вершин, ребер и областей удовлетворяют $V-E+F=0$. Например, график Титце имеет $12$ вершины, $18$ края, и $6$ регионы; $12-18+6=0$.

Конструкции

Существует множество различных способов определения геометрических поверхностей с топологией ленты Мёбиуса, что дает реализации с дополнительными геометрическими свойствами.

Проведение сегмента прямой

Лента Мёбиуса, выметаемая вращающимся отрезком во вращающейся плоскости.

Коноид Плюкера выметается другим движением отрезка.

Один из способов встроить ленту Мёбиуса в трехмерное евклидово пространство — вытеснить ее отрезком, вращающимся в плоскости, которая, в свою очередь, вращается вокруг одной из своих прямых. Чтобы скользящая поверхность встретилась сама с собой после полуповорота, отрезок прямой должен вращаться вокруг своего центра со скоростью, равной половине угловой скорости вращения плоскости. Это можно описать как параметрическую поверхность , определяемую уравнениями для декартовых координат ее точек:

$${\begin{aligned}x(u,v)&=\left(1+{\frac {v}{2}}\cos {\frac {u}{2}}\right)\cos u\\y(u,v)&=\left(1+{\frac {v}{2}}\cos {\frac {u}{2}}\right)\sin u\\z(u,v)&={\frac {v}{2}}\sin {\frac {u}{2}}\\\end{aligned}}$$

для $0\leq u<2\pi$ и $-1\leq v\leq 1$, где один параметр $u$ описывает угол поворота плоскости вокруг центральной оси и другой параметр $v$ описывает положение точки на вращающемся отрезке линии. В результате получается лента Мёбиуса шириной 1, центральная окружность которой имеет радиус 1 и лежит в $xy$-плоскость и имеет центр $(0,0,0)$. Тем же методом можно получить ленты Мёбиуса с любым нечетным числом полуповоротов за счет более быстрого вращения сегмента в его плоскости. Вращающийся сегмент сметает круговой диск в плоскости, в которой он вращается, а создаваемая им лента Мёбиуса образует срез полнотория, выметаемого этим диском. Из-за односторонности этого среза разрезанный тор остается связным.

Линия или сегмент линии, совершающие другое движение, вращаясь в горизонтальной плоскости вокруг начала координат при движении вверх и вниз, образует коноид или цилиндроид Плюкера , алгебраическую линейчатую поверхность в форме самопересекающейся ленты Мёбиуса. Он имеет применение в конструкции зубчатых передач .

Многогранные поверхности и плоские складки

Тригексафлексагон сгибается

Полоску бумаги можно образовать сплюснутую на плоскости ленту Мёбиуса, сложив ее под углом. $60^{\circ }$ углы так, чтобы его центральная линия лежала вдоль равностороннего треугольника , и соединив концы. Самая короткая полоса, для которой это возможно, состоит из трёх равносторонних треугольников, сложенных по краям в месте стыка двух треугольников. - Соотношение сторон соотношение длин полосы. по ширине – это ${\sqrt {3}}\approx 1.73$, и тот же метод сгиба работает для любого большего соотношения сторон. Для полосы из девяти равносторонних треугольников в результате получается тригексафлексагон , который можно сгибать, открывая различные части его поверхности. Если полоски слишком короткие, чтобы напрямую применить этот метод, можно сначала «сложить» полосу «гармошкой» в широком направлении вперед и назад, используя четное количество складок. Например, с двумя складками $1\times 1$ полоса станет $1\times {\tfrac {1}{3}}$ сложенная полоса, поперечное сечение которой имеет форму буквы «N», и после полуповорота она останется буквой «N». Затем более узкую полоску, сложенную гармошкой, можно сложить и соединить так же, как и более длинную полоску .

Пятивершинные многогранники и плоско сложенные ленты Мёбиуса

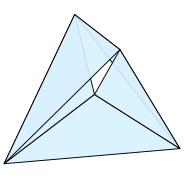
Ленту Мёбиуса также можно встроить в виде многогранной поверхности в пространстве или сложить в плоскости, при этом только пять треугольных граней имеют пять общих вершин. В этом смысле он проще цилиндра , для которого требуется шесть треугольников и шесть вершин, даже если его представить более абстрактно как симплициальный комплекс . Пятитреугольную ленту Мёбиуса наиболее симметрично можно представить пятью из десяти равносторонних треугольников четырёхмерного правильного симплекса . Эта четырехмерная многогранная лента Мёбиуса — единственная плотная лента Мёбиуса, которая полностью четырёхмерна и для которой все разрезы гиперплоскостями разделяют её на две части, топологически эквивалентные дискам или окружностям.

Другие многогранные вложения лент Мёбиуса включают одно с четырьмя выпуклыми четырехугольниками в качестве граней, другое с тремя невыпуклыми четырехугольными гранями, и один, использующий вершины и центральную точку правильного октаэдра с треугольной границей. Любую абстрактную триангуляцию проективной плоскости можно встроить в 3D как многогранную ленту Мёбиуса с треугольной границей после удаления одной из ее граней; Примером может служить шестивершинная проективная плоскость, полученная добавлением одной вершины к пятивершинной ленте Мёбиуса, соединенной треугольниками с каждым из ее граничных ребер. Однако не каждую абстрактную триангуляцию ленты Мёбиуса можно представить геометрически в виде многогранной поверхности. Для реализации необходимо и достаточно, чтобы в триангуляции не было двух непересекающихся нестягиваемых 3-циклов.

Плавно вложенные прямоугольники

Прямоугольную ленту Мёбиуса, полученную путем скрепления концов бумажного прямоугольника, можно плавно встроить в трехмерное пространство, если ее соотношение сторон превышает ${\sqrt {3}}\approx 1.73$, то же соотношение, что и для плоско сложенной версии ленты Мёбиуса в виде равностороннего треугольника. Это плоское треугольное вложение может подниматься до гладкого состояния. встраивание в трех измерениях, при котором полоса лежит плоско в трех параллельных плоскостях между тремя цилиндрическими роликами, каждый из которых касается двух плоскостей . Математически гладко вложенный лист бумаги можно смоделировать как развертывающуюся поверхность , которая может сгибаться, но не растягиваться. Поскольку его соотношение сторон уменьшается в сторону ${\sqrt {3}}$, все гладкие вложения кажутся близкими к одной и той же треугольной форме.

Продольные складки сложенной гармошкой плоской ленты Мёбиуса не позволяют ей образовывать трехмерную заделку, при которой слои отделены друг от друга и плавно изгибаются, не сминаясь и не растягиваясь из-под складок. Вместо этого, в отличие от плоско сложенного случая, существует нижний предел соотношения сторон гладких прямоугольных лент Мёбиуса. Их соотношение сторон не может быть меньше $\pi /2\approx 1.57$, даже если самопересечения разрешены. Самопересекающиеся гладкие ленты Мёбиуса существуют для любого соотношения сторон, превышающего эту границу. Без самопересечений соотношение сторон должно быть не менее

$${\frac {2}{3}}{\sqrt {3+2{\sqrt {3}}}}\approx 1.695.$$

Нерешенная задача по математике :

Может ли $12\times 7$ бумажный прямоугольник склеить встык, чтобы получилась гладкая лента Мёбиуса, погруженная в пространство?

(еще нерешенные задачи по математике)

Для соотношений сторон между этой границей и ${\sqrt {3}}$, остается открытой проблема существования гладких вложений без самопересечения . В 2023 году Ричард Шварц объявил о доказательстве того, что их не существует, но этот результат все еще ждет экспертной оценки и публикации. Если требование гладкости ослаблено, чтобы обеспечить непрерывно дифференцируемые поверхности, теорема Нэша – Койпера предполагает, что любые два противоположных края любого прямоугольника можно склеить, образуя вложенную ленту Мёбиуса, независимо от того, насколько малым становится соотношение сторон. Предельный случай, поверхность, полученная из бесконечной полосы плоскости между двумя параллельными прямыми, склеенными с противоположной ориентацией друг к другу, называется неограниченной лентой Мёбиуса или вещественным тавтологическим расслоением . Хотя оно не имеет гладкого замкнутого вложения в трехмерное пространство, его можно гладко вложить как замкнутое подмножество четырехмерного евклидова пространства.

Форма гладкой ленты Мёбиуса, склеенной из прямоугольника, с минимальной энергией не имеет известного аналитического описания, но может быть рассчитана численно и была предметом многочисленных исследований в теории пластин с момента первой работы Майкла по этому вопросу в 1930 году. Садовский . Также можно найти алгебраические поверхности , содержащие прямоугольные развертывающиеся ленты Мёбиуса.

Создание границы круглой

Склеивание двух лент Мёбиуса в бутылку Клейна.

Проекция суданской ленты Мёбиуса.

Край или ленты Мёбиуса топологически эквивалентна окружности граница . В обычных формах ленты Мёбиуса она имеет форму, отличную от круга, но не завязана , и поэтому всю ленту можно растягивать, не пересекая себя, чтобы сделать край идеально круглым. Один из таких примеров основан на топологии бутылки Клейна — односторонней поверхности без границ, которую нельзя встроить в трехмерное пространство, но можно погрузить (позволяя поверхности пересекать себя определенными ограниченными способами). Бутылка Клейна — это поверхность, которая получается, когда две ленты Мёбиуса склеиваются друг с другом, и — обращая этот процесс вспять — бутылку Клейна можно разрезать по тщательно выбранному разрезу, чтобы получить две ленты Мёбиуса. Для формы бутылки Клейна, известной как бутылка Клейна Лоусона, кривая, по которой она разрезается, может быть сделана круглой, в результате чего получаются ленты Мёбиуса с круглыми краями.

Бутылка Клейна Лоусона — это самопересекающаяся минимальная поверхность в единичной гиперсфере четырёхмерного пространства, набор точек вида

$$(\cos \theta \cos \phi ,\sin \theta \cos \phi ,\cos 2\theta \sin \phi ,\sin 2\theta \sin \phi )$$

для $0\leq \theta <\pi ,0\leq \phi <2\pi$. Половина этой бутылки Клейна, часть с $0\leq \phi <\pi$, дает ленту Мёбиуса, вложенную в гиперсферу как минимальную поверхность с большим кругом в качестве ее границы. Это вложение иногда называют «суданской лентой Мёбиуса» в честь топологов Сью Гудман и Дэниела Азимова, открывших ее в 1970-х годах. Геометрически бутылку Клейна Лоусона можно построить, проведя большой круг посредством большого кругового движения в трехмерной сфере, а суданскую ленту Мёбиуса можно получить, проведя полукруг вместо круга, или, что то же самое, разрезав бутылку Клейна по кругу. перпендикулярно всем очерченным кругам. Стереографическая проекция преобразует эту форму из трехмерного сферического пространства в трехмерное евклидово пространство, сохраняя округлость его границ. Наиболее симметричная проекция получается при использовании точки проекции, которая лежит на большом круге, проходящем через середину каждого из полукругов, но создает неограниченное вложение с точкой проекции, удаленной от его центральной линии. Вместо этого, если суданскую ленту Мёбиуса оставить непроецированной в 3-сфере, она останется с бесконечной группой симметрий, изоморфной ортогональной группе. $\mathrm {O} (2)$, группа симметрий окружности .

Схематическое изображение крестовины с открытым дном с указанием наборов ее уровней . Эта поверхность пересекает себя по вертикальному отрезку.

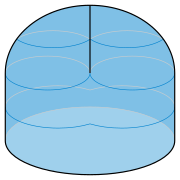
Суданская лента Мёбиуса простирается со всех сторон пограничного круга, что неизбежно, если поверхность не хочет пересекать сама себя. Другая форма ленты Мёбиуса, называемая крестовиной или крестовиной , также имеет круговую границу, но в остальном остается только на одной стороне плоскости этой окружности. что делает его более удобным для крепления к круглым отверстиям на других поверхностях. Для этого он крестится. Его можно образовать, удалив четырехугольник из вершины полусферы, ориентируя края четырехугольника в чередующихся направлениях, а затем склеивая противоположные пары этих ребер в соответствии с этой ориентацией. Две части поверхности, образованные двумя склеенными парами кромок, пересекают друг друга с точками защемления, подобными точкам зонтика Уитни, на каждом конце пересекающегося сегмента. та же топологическая структура, что и в коноиде Плюкера .

Поверхности постоянной кривизны

Открытая лента Мёбиуса — это относительная внутренняя часть стандартной ленты Мёбиуса, образованная путём исключения точек на её граничном крае. Ему может быть задана риманова геометрия постоянной положительной, отрицательной или нулевой гауссовой кривизны . Случаи отрицательной и нулевой кривизны образуют геодезически полные поверхности, а это означает, что все геодезические («прямые линии» на поверхности) могут продолжаться бесконечно в любом направлении.

Нулевая кривизна

Разомкнутую полосу нулевой кривизны можно построить, склеив противоположные стороны плоской полосы между двумя параллельными линиями, описанными выше как тавтологическое расслоение линий. Полученная метрика превращает открытую ленту Мёбиуса в (геодезически) полную плоскую поверхность (т. е. имеющую всюду нулевую гауссову кривизну). Это уникальная метрика на ленте Мёбиуса с точностью до равномерного масштабирования, которая одновременно плоская и полная. Это факторпространство плоскости по скользящему отражению и (вместе с плоскостью, цилиндром , тором и бутылкой Клейна ) является одним из пяти двумерных полных плоских многообразий .

Отрицательная кривизна

Открытая лента Мёбиуса допускает также полные метрики постоянной отрицательной кривизны. Один из способов убедиться в этом — начать с модели верхней полуплоскости (Пуанкаре) гиперболической плоскости , геометрии постоянной кривизны, линии которой представлены в модели полукругами, пересекающимися с $x$-ось под прямым углом. Возьмите подмножество верхней полуплоскости между любыми двумя вложенными полукругами и отождествите внешний полукруг с переворотом внутреннего полукруга влево-вправо. В результате получается топологически полная и некомпактная лента Мёбиуса с постоянной отрицательной кривизной. Это «нестандартная» полная гиперболическая поверхность в том смысле, что она содержит полную гиперболическую полуплоскость (на самом деле две, на противоположных сторонах оси скольжения-отражения) и является одной из всего 13 нестандартных поверхностей. Опять же, это можно понимать как частное гиперболической плоскости к скользящему отражению.

Положительная кривизна

Лента Мёбиуса постоянной положительной кривизны не может быть полной, так как известно, что единственными полными поверхностями постоянной положительной кривизны являются сфера и проективная плоскость . Однако в некотором смысле от полной поверхности отделяет всего одну точку, поскольку открытая лента Мёбиуса гомеоморфна однажды проколотой проективной плоскости, поверхности, полученной удалением любой одной точки из проективной плоскости.

Минимальные поверхности описываются как имеющие постоянную нулевую среднюю кривизну вместо постоянной гауссовой кривизны. Суданская лента Мёбиуса была построена как минимальная поверхность, ограниченная большим кругом в 3-сфере, но существует также уникальная полная (без границ) минимальная поверхность, погруженная в евклидово пространство, имеющая топологию открытой ленты Мёбиуса. Она называется лентой Микса Мёбиуса. после описания Уильямом Гамильтоном Миксом в 1982 году, III . Несмотря на глобальную нестабильность как минимальная поверхность, небольшие ее участки, ограниченные несжимаемыми кривыми внутри поверхности, могут образовывать стабильные вложенные ленты Мёбиуса как минимальные поверхности. И полоса Микса Мёбиуса, и каждая минимальная поверхность более высокой размерности с топологией ленты Мёбиуса могут быть построены с использованием решений задачи Бьёрлинга , которая определяет минимальную поверхность однозначно по её граничной кривой и касательным плоскостям вдоль этой кривой.

Пространства строк

Семейству линий на плоскости можно придать структуру гладкого пространства, где каждая линия представлена ​​как точка в этом пространстве. Полученное пространство линий топологически эквивалентно открытой ленте Мёбиуса. Один из способов убедиться в этом — расширить евклидову плоскость до реальной проективной плоскости, добавив еще одну линию, линию, находящуюся на бесконечности . В силу проективной двойственности пространство прямых на проективной плоскости эквивалентно пространству точек, самой проективной плоскости. Удаление бесконечной линии для создания пространства евклидовых линий прокалывает это пространство проективных линий. Следовательно, пространство евклидовых прямых представляет собой проколотую проективную плоскость, являющуюся одной из форм открытой ленты Мёбиуса. Пространство линий на гиперболической плоскости можно параметризовать неупорядоченными парами различных точек окружности, парами точек на бесконечности каждой прямой. Это пространство опять-таки имеет топологию открытой ленты Мёбиуса.

Эти пространства линий очень симметричны. Симметрии евклидовых прямых включают аффинные преобразования , а симметрии гиперболических прямых включают преобразования Мёбиуса . Аффинные преобразования и преобразования Мёбиуса образуют 6-мерные группы Ли , топологические пространства, имеющие совместимую алгебраическую структуру, описывающую композицию симметрий. Поскольку каждая линия на плоскости симметрична любой другой прямой, открытая лента Мёбиуса представляет собой однородное пространство , пространство с симметриями, которые переводят каждую точку в любую другую точку. Однородные пространства групп Ли называются солвмногообразиями , а полосу Мёбиуса можно использовать в качестве контрпримера , показывающего, что не каждое солвмногообразие является нильмногообразием и что не каждое солвмногообразие можно разложить в прямое произведение компактного солвмногообразия с $\mathbb {R} ^{n}$. Эти симметрии также предоставляют другой способ построить саму ленту Мёбиуса как групповую модель этих групп Ли. Групповая модель состоит из группы Ли и подгруппы стабилизатора ее действия; сжатие смежных классов подгруппы до точек создает пространство с той же топологией, что и лежащее в основе однородное пространство. В случае симметрий евклидовых прямых стабилизатор $x$-ось состоит из всех симметрий, которые переводят ось в себя. Каждая строка $\ell$ соответствует смежному классу, набору симметрий, которые отображают $\ell$ к $x$-ось. Следовательно, факторпространство , пространство, которое имеет одну точку на каждый смежный класс и наследует свою топологию от пространства симметрий, совпадает с пространством прямых и снова является открытой лентой Мёбиуса.

Приложения

Электрический поток в резисторе Мёбиуса

Помимо уже обсуждавшихся применений лент Мёбиуса для проектирования механических ремней, которые изнашиваются равномерно по всей поверхности, а также коноида Плюкера для проектирования зубчатых колес, другие применения лент Мёбиуса включают:

• Графеновые ленты скручены в ленты Мёбиуса с новыми электронными характеристиками, включая спиральный магнетизм.
• Ароматичность Мёбиуса — свойство органических химических веществ , молекулярная структура которых образует цикл, при этом молекулярные орбитали выстраиваются вдоль цикла по образцу ленты Мёбиуса.
• Резистор Мёбиуса — полоска проводящего материала, покрывающая одну сторону диэлектрической ленты Мёбиуса таким образом, что компенсирует собственную самоиндукцию.
• Резонаторы компактной конструкции и резонансной частотой, вдвое меньшей, чем у линейных катушек идентичной конструкции.
• Паттерны поляризации света, выходящего из q - пластины
• Доказательство невозможности непрерывных, анонимных и единогласных правил двухсторонней агрегации в теории социального выбора.
• Американские горки с петлей Мёбиуса , разновидность двухпутных американских горок, в которых две дорожки вращаются вокруг друг друга нечетное количество раз, так что вагоны возвращаются на другую дорожку, отличную от той, с которой они начали.
• Карты мира, проецируемые на ленту Мёбиуса, с удобными свойствами: отсутствие границ с востока на запад и антипод любой точки на карте можно найти на другой напечатанной стороне поверхности в той же точке ленты Мёбиуса.

Ученые также изучили энергетику мыльных пленок в форме лент Мёбиуса. химический синтез молекул, имеющих форму ленты Мёбиуса, и формирование более крупных наноразмерных лент Мёбиуса с помощью ДНК-оригами .

В популярной культуре

Бесконечный поворот , Макс Билл , 1956, из Музея скульптур под открытым небом Миддельхейма.

Двумерные произведения искусства с изображением ленты Мёбиуса включают безымянную картину Коррадо Кальи 1947 года (увековеченную в стихотворении Чарльза Олсона ), и две гравюры М. К. Эшера : Лента Мебиуса I (1961), изображающая трех сложенных камбал , кусающих друг друга за хвосты; и Лента Мёбиуса II (1963), изображающая муравьев, ползающих по ленте Мёбиуса в форме лемнискаты . Это также популярный предмет математической скульптуры , включая работы Макса Билла ( «Бесконечная лента» , 1953), Хосе де Ривера ( «Бесконечность» , 1967) и Себастьяна . Лента Мёбиуса , завязанная трилистником, использовалась в фильме Джона Робинсона « Бессмертие » (1982). » Чарльза О. Перри ( «Континуум 1976) — одно из нескольких произведений Перри, исследующих варианты ленты Мёбиуса.

Символ переработки

Логотип Google Диска (2012–2014 гг.)

Логотип IMPA на марке

Благодаря своей легко узнаваемой форме ленты Мёбиуса являются распространенным элементом графического дизайна . Знакомый с тремя стрелками логотип переработки отходов , разработанный в 1970 году, основан на гладкой треугольной форме ленты Мёбиуса. как и логотип экологической выставки Expo '74 . В некоторых вариантах символа переработки используется другое вложение с тремя полуповоротами вместо одного. а в оригинальной версии логотипа Google Drive использовалась сложенная в три раза лента Мёбиуса, как и в других подобных дизайнах. Бразильский национальный институт математики Pura e Aplicada (IMPA) использует стилизованную гладкую ленту Мёбиуса в качестве своего логотипа, а в их здании выставлена ​​​​соответствующая большая скульптура ленты Мёбиуса. Лента Мёбиуса также использовалась в оформлении почтовых марок таких стран, как Бразилия, Бельгия, Нидерланды и Швейцария.

Зал славы NASCAR Вход в

Ленты Мёбиуса часто служили источником вдохновения для архитектурного проектирования зданий и мостов. Однако многие из них представляют собой проекты или концептуальные проекты, а не построенные объекты, или расширяют свою интерпретацию ленты Мёбиуса за пределы ее узнаваемости как математической формы или функциональной части архитектуры. Примером может служить Национальная библиотека Казахстана , для которой было запланировано здание в форме утолщенной ленты Мёбиуса, но после того, как первоначальные архитекторы отказались от проекта, его отремонтировали с другим дизайном. Одним из примечательных зданий с лентой Мёбиуса является Зал славы NASCAR , окруженный большой витой лентой из нержавеющей стали, служащей фасадом и навесом и напоминающей изогнутые формы гоночных трасс. В меньшем масштабе стул Мебиуса (2006 г.) от Педро Рейеса представляет собой скамейку для ухаживания, основание и боковые стороны которой имеют форму ленты Мёбиуса. В качестве формы математики и волоконного искусства шарфы вязали из . лент Мёбиуса со времен работ Элизабет Циммерманн в начале 1980-х годов В кулинарии ленты Мёбиуса используются для нарезки бубликов . делаем петельки из бекона , и создание новых форм для макарон .

Хотя с математической точки зрения лента Мёбиуса и четвертое измерение являются чисто пространственными концепциями, в спекулятивной фантастике они часто используются как основа временной петли , в которую могут попасть неосторожные жертвы. Примерами этого образа являются Мартина Гарднера ( «Бессторонний профессор» » Армина Джозефа Дойча ( 1946), « Метро по имени Мебиус фильм «Мебиус» 1950) и основанный на нем (1996). Целый мир, имеющий форму ленты Мёбиуса, является местом действия «Стены тьмы» Артура Кларка (1946), в то время как обычные ленты Мёбиуса используются в качестве умных изобретений во многих рассказах Уильяма Хэзлетта Апсона 1940-х годов. Другие художественные произведения были проанализированы как имеющие структуру, подобную ленте Мёбиуса, в которой элементы сюжета повторяются с изюминкой; К ним относятся Марселя Пруста « В поисках утраченного времени» (1913–1927), Луиджи Пиранделло «Шесть персонажей в поисках автора» (1921), Фрэнка Капры » « Эта чудесная жизнь (1946), « Затерянные в «Дом веселья» (1968), Сэмюэля Р. Делани ( » «Далгрен 1975) и фильм «Донни Дарко» (2001).

Один из музыкальных канонов И. С. Баха , пятый из 14 канонов ( BWV 1087 ), обнаруженный в 1974 году в баховской копии « Гольдберг-вариаций» , отличается симметрией скольжения и отражения , при которой каждый голос в каноне повторяет с перевернутыми нотами одно и то же. мотив из двух тактов ранее. Из-за этой симметрии партитуру этого канона можно считать записанной на ленте Мёбиуса. В теории музыки тона, отличающиеся на октаву, обычно считаются равнозначными нотами, а пространство возможных нот образует круг — хроматический круг . Поскольку лента Мёбиуса представляет собой конфигурационное пространство двух неупорядоченных точек окружности, пространство всех двухнотных аккордов принимает форму ленты Мёбиуса. Эта концепция и ее обобщения на другие аспекты представляют собой важное применение орбифолдов в теории музыки . Современные музыкальные группы, получившие свое название от ленты Мёбиуса, включают американское электронное рок-трио Mobius Band. и норвежская прогрессив-рок-группа Ring Van Möbius .

Ленты Мёбиуса и их свойства использовались при оформлении сценического фокуса . Один из таких трюков, известный как афганские ленты, основан на том факте, что лента Мёбиуса, если ее разрезать вдоль, остается единой. Он зародился в 1880-х годах и был очень популярен в первой половине ХХ века. Существует множество версий этого трюка, которые исполнялись известными иллюзионистами, такими как Гарри Блэкстоун-старший и Томас Нельсон Даунс .

См. также

• Счетчик Мёбиуса — сдвиговый регистр, выходной бит которого дополняется перед передачей обратно во входной бит.
• Треугольник Пенроуза — невозможная фигура, граница которой, кажется, обертывается вокруг нее лентой Мёбиуса.
• Теория ленты — математическая теория бесконечно тонких полосок, следующих за узловатыми пространственными кривыми.
• Аттрактор Смейла-Вильямса , фрактал, образованный путем многократного утолщения пространственной кривой до ленты Мёбиуса и последующей замены ее граничным краем.
• Пупочный тор

Внешние ссылки

• СМИ, связанные с лентой Мебиуса , на Викискладе?
• Вайсштейн, Эрик В. «Лента Мёбиуса» . Математический мир .