Циклическая группа

В абстрактной алгебре циклическая группа или моногенная группа — это группа , обозначаемая C _n (также часто $\mathbb {Z}$_n или Z _n (не путать с коммутативным кольцом p -адических чисел) , которое порождается одним элементом. То есть это набор обратимых такой , элементов с одной ассоциативной бинарной операцией , и он содержит элемент g что любой другой элемент группы может быть получен путем многократного применения групповой операции к g или ее обратной операции. Каждый элемент может быть записан как целая степень g в мультипликативной записи или как целое число, кратное g в аддитивной записи. Этот элемент g называется генератором группы.

Каждая бесконечная циклическая группа аддитивной группе Z , изоморфна целых чисел . Каждая конечная циклическая группа порядка   n изоморфна аддитивной группе Z / n Z , целых чисел по модулю   n . Каждая циклическая группа является абелевой группой (это означает, что ее групповая операция коммутативна ), и каждая конечно порожденная абелева группа является прямым произведением циклических групп.

Любая циклическая группа простого порядка является простой группой , которую нельзя разбить на более мелкие группы. В классификации конечных простых групп один из трёх бесконечных классов состоит из циклических групп простого порядка. Таким образом, циклические группы простого порядка входят в число строительных блоков, из которых могут быть построены все группы.

Определение и обозначения

Шесть комплексных корней шестой степени из единицы при умножении образуют циклическую группу. Здесь z — генератор, а z ² это не так, потому что его степени не могут дать нечетные степени z .

Для любого элемента g в любой группе G можно сформировать подгруппу , состоящую из всех его целых степеней: ⟨ g ⟩ = { g ^к | k ∈ Z } , называемая циклической подгруппой, порожденной g . Порядок ⟩ g | равен |⟨ g ⟩|, количеству элементов в ⟨ g , обычно сокращенно g |, как ord( g ) или как o( g ). То есть порядок элемента равен порядку циклической подгруппы, которую он порождает.

Циклическая группа которая равна одной из своих циклических подгрупп: G = ⟨ g ⟩ для некоторого элемента g называемого генератором G. — это группа , ,

Для конечной циклической группы   G порядка n имеем G = { e , g , g ² , ... , г ^{п -1} } , где e — единичный элемент, а g ^я = г ^дж всякий раз, когда я ≡ j ( mod   n ); в частности г ^н = г ⁰ = е и г ⁻¹ = г ^{п -1} . Абстрактную группу, определяемую этим умножением, часто обозначают Cn _, и мы говорим, что стандартной циклической G изоморфна группе _Cn . Такая группа также изоморфна Z / n Z , группе целых чисел по модулю n с операцией сложения, которая является стандартной циклической группой в аддитивной записи. При изоморфизме χ , определяемом χ ( g ^я ) = i единичный элемент e соответствует 0, произведения соответствуют суммам, а степени соответствуют кратным.

Например, набор комплексных корней шестой степени из единицы:

$$G=\left\{\pm 1,\pm {\left({\tfrac {1}{2}}+{\tfrac {\sqrt {3}}{2}}i\right)},\pm {\left({\tfrac {1}{2}}-{\tfrac {\sqrt {3}}{2}}i\right)}\right\}$$

образует группу при умножении. Он циклический, так как порождается примитивным корнем $z={\tfrac {1}{2}}+{\tfrac {\sqrt {3}}{2}}i=e^{2\pi i/6}:$ то есть G знак равно ⟨ z ⟩ знак равно { 1, z , z ² , С ³ , С ⁴ , С ⁵ } с z ⁶ = 1. При замене букв она изоморфна (структурно такая же, как) стандартной циклической группе порядка 6, определяемой как C ₆ = ⟨ g ⟩ = { e , g , g ² , г ³ , г ⁴ , г ⁵ } с умножением g ^дж · г ^к = г ^{дж + к (против 6)} , так что г ⁶ = г ⁰ = е . Эти группы также изоморфны Z /6 Z = {0, 1, 2, 3, 4, 5} с операцией сложения по модулю 6, с z ^к и г ^к соответствующий к . Например, 1 + 2 ≡ 3 (по модулю 6) соответствует z ¹ · С ² = г ³ , а 2 + 5 ≡ 1 (mod 6) соответствует z ² · С ⁵ = г ⁷ = г ¹ , и так далее. Любой элемент порождает свою циклическую подгруппу, например ⟨ z ² ⟩ знак равно { е , z ² , С ⁴ } порядка 3, изоморфный C ₃ и Z /3 Z ; и ⟨ г ⁵ ⟩ знак равно { е , z ⁵ , С ¹⁰ = г ⁴ , С ¹⁵ = г ³ , С ²⁰ = г ² , С ²⁵ = z } = G , так что z ⁵ и является альтернативным генератором G. имеет порядок 6

Вместо частных обозначений Z / n Z , Z /( n ) или Z / n некоторые авторы обозначают конечную циклическую группу как Z _n , но это противоречит обозначениям теории чисел , где Z _p обозначает p -адическую группу. числовое кольцо, или локализация в простом идеале .

Бесконечные циклические группы

p1, ( *∞∞ )	p11g, (22∞)
Две группы изоморфны Z. фризов При одном генераторе у p1 есть трансляции, а у p11g — скользящие отражения.

С другой стороны, в бесконечной циклической группе G = ⟨ g ⟩ степени g ^к дать различные элементы для всех целых чисел k , так что G = { ... , g ⁻² , г ⁻¹ , яйцо ​ ​ ​ ​ ² , ... }, а G изоморфна стандартной группе C = C _∞ и Z , аддитивной группе целых чисел. Примером может служить первая группа фриза . Здесь нет конечных циклов, и название «циклический» может ввести в заблуждение.

Чтобы избежать этой путаницы, Бурбаки ввел термин «моногенная группа» для группы с одним генератором и ограничил «циклическую группу» так, чтобы она обозначала конечную моногенную группу, избегая термина «бесконечная циклическая группа».

Примеры

Примеры циклических групп вращательной симметрии

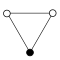
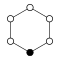
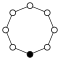
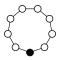
С 1	С 2	С 3
С 4	CС5	CС6

Целочисленное и модульное сложение

Множество целых чисел   Z с помощью операции сложения образует группу. Это бесконечная циклическая группа , поскольку все целые числа можно записать путем многократного сложения или вычитания одного числа 1. В этой группе единственными образующими являются 1 и -1. изоморфна Z. Любая бесконечная циклическая группа

Для каждого положительного целого числа n набор целых чисел по модулю   n , опять же с операцией сложения, образует конечную циклическую группу, Z / n Z. обозначаемую Модульное целое число i является генератором этой группы, если i с взаимно просто n , поскольку эти элементы могут генерировать все остальные элементы группы путем сложения целых чисел. (Число таких образующих равно φ ( n ), где φ — функция тотента Эйлера .) Любая конечная циклическая группа G изоморфна Z / n Z , где n = | г | это порядок группы.

Операции сложения целых и модулярных целых чисел, используемые для определения циклических групп, представляют собой операции сложения коммутативных колец , также обозначаемых Z и Z / n Z или Z /( n ). Если p — простое число , то Z / p Z — конечное поле и обычно обозначается F _p или GF( p ) для поля Галуа.

Модульное умножение

Основная статья: Мультипликативная группа целых чисел по модулю n

Для каждого положительного целого числа n набор целых чисел по модулю n , которые являются относительно простыми с n, записывается как ( Z / n Z ) ^× ; он образует группу при операции умножения. Эта группа не всегда является циклической, но она является циклической всякий раз, когда n равно 1, 2, 4, степени нечетного простого числа или удвоенной степени нечетного простого числа (последовательность A033948 в OEIS ). Это мультипликативная группа единиц кольца Z / n Z ; их φ ( n ), где снова φ — функция тотента Эйлера . Например, ( Z /6 Z ) ^× = {1, 5}, и поскольку 6 — дважды нечетное простое число, это циклическая группа. Напротив, ( Z /8 Z ) ^× = {1, 3, 5, 7} является 4-группой Клейна и не является циклической. Когда ( З / н З ) ^× является циклическим, его образующие называются примитивными корнями по модулю n .

Для простого числа p группа ( Z / p Z ) ^× всегда циклический, состоящий из ненулевых элементов конечного поля порядка p . В более общем смысле, каждая конечная подгруппа мультипликативной группы любого поля является циклической.

Вращательная симметрия

Основная статья: Вращательная симметрия

Множество вращательных симметрий многоугольника образует конечную циклическую группу. Если существует n различных способов перемещения многоугольника к самому себе поворотом (включая нулевое вращение), то эта группа симметрии Z / n Z. изоморфна В трех или более высоких измерениях существуют другие конечные группы симметрии, которые являются циклическими , но которые не все представляют собой вращения вокруг оси, а вместо этого являются роторными отражениями .

Группа всех вращений окружности ( группа окружностей , также обозначается S ¹ ) не является циклическим, поскольку не существует одного вращения, целочисленные степени которого порождают все вращения. Действительно, бесконечная циклическая группа _C∞ счетна , а S ¹ не является. Группа поворотов на рациональные углы счетна , но все же не циклична.

Теория Галуа

Корень n- й степени из единицы — это комплексное число которого n-я степень равна 1, корень многочлена , x ^н − 1 . Множество всех корней n-й степени из единицы образует циклическую группу порядка n при умножении. Образующими этой циклической группы являются примитивные корни n-й степени из единицы ; они являются корнями n- го кругового многочлена . Например, полином z ³ − 1 фактор как ( z − 1)( z − ω )( z − ω ² ) , где ω = e ^{2 πи /3} ; множество {1, ω , ω ² } = { ох ⁰ , ой ¹ , ой ² } образует циклическую группу при умножении. Группа Галуа рациональных расширения поля чисел , порожденная корнями n- й степени из единицы, образует другую группу, изоморфную мультипликативной группе ( Z/ n Z ). ^× порядка φ ( n ) , который является циклическим для некоторых, но не для всех n (см. выше).

Расширение поля называется циклическим расширением , если его группа Галуа циклическая. Для полей нулевой характеристики такие расширения являются предметом теории Куммера и тесно связаны с радикальной разрешимостью . Для расширения конечных полей характеристики p его группа Галуа всегда конечна и циклична, порождена степенью отображения Фробениуса . И наоборот, для данного конечного поля F и конечной циклической группы G существует конечное расширение поля F , группой Галуа которого является G .

Подгруппы

Основная статья: Основная теорема о циклических группах

Все подгруппы и факторгруппы циклических групп циклические. В частности, все подгруппы Z имеют вид ⟨ m ⟩ = m Z , где m — положительное целое число. Все эти подгруппы отличны друг от друга и, за исключением тривиальной группы {0} = 0 , все они изоморфны Z Z . Решетка подгрупп группы Z изоморфна двойственной решетке натуральных чисел, упорядоченных по делимости . Таким образом, поскольку простое число p не имеет нетривиальных делителей, Z является максимальной собственной подгруппой, а факторгруппа Z / p Z проста p ; на самом деле циклическая группа проста тогда и только тогда, когда ее порядок прост.

Все факторгруппы Z / n Z конечны, за исключением Z /0 Z = Z /{0}. Для каждого положительного делителя d числа n факторгруппа Z / n Z имеет ровно одну подгруппу порядка d , порожденную вычетов классом n / d . Других подгрупп нет.

Дополнительные свойства

Любая циклическая группа абелева . То есть его групповая операция коммутативна : gh = hg (для всех g и h в G ). Это ясно для групп целочисленного и модулярного сложения, поскольку r + s ≡ s + r (mod n ) , и это следует для всех циклических групп, поскольку все они изоморфны этим стандартным группам. Для конечной циклической группы n g порядка ^н является единичным элементом для любого элемента g . Это снова следует из использования изоморфизма модулярного сложения, поскольку kn ≡ 0 (mod n ) для каждого целого числа k . (Это также верно для общей группы порядка n в силу теоремы Лагранжа .)

Для высшей власти $p^{k}$, группа $Z/p^{k}Z$называется первичной циклической группой . Фундаментальная теорема об абелевых группах утверждает, что каждая конечно порожденная абелева группа является конечным прямым произведением примарных циклических и бесконечных циклических групп.

Поскольку циклическая группа абелева, каждый из ее классов сопряженности состоит из одного элемента. Таким образом , циклическая группа порядка n имеет n классов сопряженности.

Если d является делителем n , , то количество элементов в Z / n Z , имеющих порядок d, равно φ ( d ), а количество элементов, порядок которых делит d равно ровно d . Если G — конечная группа, в которой для каждого n > 0 n G содержит не более n элементов порядка, делящего , то G должна быть циклической. Порядок элемента m в Z / n Z равен n / НОД ( n , m ).

Если n и m , взаимно просты то прямое произведение двух циклических групп Z / n Z и Z / m Z изоморфно циклической группе Z / nm Z , и обратное также справедливо: это одна из форм китайской теоремы об остатках . Например, Z /12 Z изоморфно прямому произведению Z /3 Z × Z /4 Z при изоморфизме ( k mod 12) → ( k mod 3, k mod 4) ; но он не изоморфен Z /6 Z × Z /2 Z , в котором каждый элемент имеет порядок не выше 6.

Если p — простое число любая группа с p элементами изоморфна простой группе Z / p Z. , то Число n называется циклическим числом , если Z / n Z — единственная группа порядка n , что верно именно тогда, когда gcd( n , φ ( n )) = 1 . Последовательность циклических чисел включает все простые числа, но некоторые из них являются составными , например 15. Однако все циклические числа нечетны, кроме 2. Циклическими числами являются:

1, 2, 3, 5, 7, 11, 13, 15, 17, 19, 23, 29, 31, 33, 35, 37, 41, 43, 47, 51, 53, 59, 61, 65, 67, 69, 71, 73, 77, 79, 83, 85, 87, 89, 91, 95, 97, 101, 103, 107, 109, 113, 115, 119, 123, 127, 131, 133, 137, 139, 141, 143, ... (последовательность A003277 в OEIS )

Из определения сразу следует, что циклические группы имеют групповое представление C _∞ = ⟨ x | ⟩ и C _n знак равно ⟨ Икс | Икс ^н ⟩ для конечного n .

Связанные объекты

Представления

Теория представлений циклической группы является критическим базовым случаем теории представлений более общих конечных групп. В сложном случае представление циклической группы разлагается в прямую сумму линейных характеров, что делает связь между теорией характеров и теорией представлений прозрачной. В случае положительной характеристики неразложимые представления циклической группы образуют модель и индуктивную основу для теории представлений групп с циклическими силовскими подгруппами и, в более общем плане, теории представлений блоков циклического дефекта.

График цикла

Дополнительная информация: Граф цикла (алгебра).

Граф циклов иллюстрирует различные циклы группы и особенно полезен при визуализации структуры небольших конечных групп . Граф циклов для циклической группы — это просто круговой граф , где порядок группы равен количеству узлов. Один генератор определяет группу как направленный путь на графе, а обратный генератор определяет обратный путь. Тривиальный путь (идентификатор) может быть нарисован в виде цикла , но обычно он подавляется. Z ₂ иногда изображается с двумя изогнутыми краями как мультиграф .

Циклическая группа Z _n порядка n соответствует одному циклу, изображенному просто в виде n -стороннего многоугольника с элементами в вершинах.

Циклические графики до 24 порядка

С 1	ZZ2	ZZ3	ZZ4	З 5	Z 6 = Z 3 ×Z 2	З 7	З 8
ZZ9	Z 10 = Z 5 ×Z 2	С 11	Z 12 = Z 4 ×Z 3	З 13	Z 14 = Z 7 ×Z 2	Z 15 = Z 5 ×Z 3	С 16
З 17	Z 18 = Z 9 ×Z 2	З 19	Z 20 = Z 5 ×Z 4	Z 21 = Z 7 ×Z 3	Z 22 = Z 11 × Z 2	З 23	Z 24 = Z 8 ×Z 3

Граф Кэли

Основная статья: Циркулянтный граф

Граф Пэли порядка 13, циркулянтный граф, сформированный как граф Кэли Z / 13 с набором генераторов {1,3,4}

Граф Кэли — это граф, определенный из пары ( G , S ), где G — группа, а S — набор образующих группы; у него есть вершина для каждого элемента группы и ребро для каждого произведения элемента с генератором. В случае конечной циклической группы с ее единственным генератором граф Кэли является графом циклов , а для бесконечной циклической группы с ее генератором граф Кэли является дважды бесконечным графом путей . Однако графы Кэли могут быть определены и из других наборов генераторов. Графы Кэли циклических групп с произвольными порождающими множествами называются циркулянтными графами . Эти графики могут быть представлены геометрически как набор равноотстоящих друг от друга точек на круге или на линии, где каждая точка соединена с соседями с тем же набором расстояний, что и каждая другая точка. Это в точности вершинно-транзитивные графы, которых группа симметрии включает транзитивную циклическую группу.

Эндоморфизмы

Кольцо эндоморфизмов абелевой Z / n Z изоморфно как самому Z / n Z кольцу . группы При этом изоморфизме число r соответствует эндоморфизму Z / n Z , который отображает каждый элемент в сумму r его копий. Это биекция тогда и только тогда, когда r взаимно прост с n , поэтому группа автоморфизмов Z / n Z изоморфна единичной группе ( Z / n Z ). ^× .

Аналогично кольцо эндоморфизмов аддитивной группы Z изоморфно кольцу Z . Его группа автоморфизмов изоморфна группе единиц кольца Z , которая равна ({−1, +1}, ×) ≅ C ₂ .

циклических

что тензорное произведение Z / m Z ⊗ Z / n Z изоморфно Z /gcd( m , n ) Z. Можно показать , Таким образом, мы можем сформировать коллекцию гомоморфизмов групп от Z / m Z до Z / n Z , обозначаемую hom( Z / m Z , Z / n Z ) , которая сама является группой.

Для тензорного произведения это является следствием того общего факта, что R / I ⊗ _R R / J ≅ R /( I + J ) , где R — коммутативное кольцо с единицей, а I и J — идеалы кольца. Что касается группы Hom, напомним, что она изоморфна подгруппе Z / n Z , состоящей из элементов порядка, делящего m . Эта подгруппа является циклической порядка gcd( m , n ) , что завершает доказательство.

Родственные классы групп

Несколько других классов групп были определены по их отношению к циклическим группам:

Практически циклические группы

Группа называется практически циклической, если она содержит циклическую подгруппу конечного индекса (количества смежных классов , которые имеет подгруппа). Другими словами, любой элемент практически циклической группы можно получить перемножением члена циклической подгруппы и члена некоторого конечного множества. Любая циклическая группа практически циклична, как и любая конечная группа. Бесконечная группа практически циклична тогда и только тогда, когда она конечно порождена и имеет ровно два конца ; примером такой группы является прямое произведение Z / n Z и Z , в котором фактор Z имеет конечный индекс n . Каждая абелева подгруппа гиперболической группы Громова практически циклическая.

Проциклические группы

называется Проконечная группа проциклической, если она топологически порождается одним элементом. Примеры проконечных групп включают бесконечные целые числа. ${\widehat {\mathbb {Z} }}$ или p -адические целые числа $\mathbb {Z} _{p}$ для простого числа p .

Локально циклические группы

Основная статья: Локально циклическая группа

— Локально циклическая группа это группа, в которой каждая конечно порожденная подгруппа является циклической. Примером является аддитивная группа рациональных чисел : каждый конечный набор рациональных чисел представляет собой набор целых кратных одной единичной дроби , обратной их наименьшему общему знаменателю , и порождает в качестве подгруппы циклическую группу целых кратных этой дроби. единица дроби. Группа является локально циклической тогда и только тогда, когда ее решетка подгрупп является дистрибутивной решеткой .

Циклически упорядоченные группы

Основная статья: Циклически упорядоченная группа

— Циклически упорядоченная группа это группа вместе с циклическим порядком , сохраняемым структурой группы. Каждой циклической группе можно придать структуру как циклически упорядоченную группу, соответствующую порядку целых чисел (или целых чисел по модулю порядка группы). Любая конечная подгруппа циклически упорядоченной группы является циклической.

Метациклические и полициклические группы

Метациклическая группа — это группа, содержащая циклическую нормальную подгруппу , фактор которой также является циклическим. Эти группы включают циклические группы, дициклические группы и прямые продукты двух циклических групп. Полициклические группы обобщают метациклические группы, допуская более одного уровня расширения группы . Группа является полициклической, если она имеет конечную убывающую последовательность подгрупп, каждая из которых нормальна в предыдущей подгруппе с циклическим фактором, заканчивающимся тривиальной группой. Любая конечно порожденная абелева группа или нильпотентная группа полициклична.

См. также

• График цикла (группа)
• Циклический модуль
• Циклическое просеивание
• Группа Прюфера ( счетный бесконечный аналог)
• Группа кругов ( несчетно бесконечный аналог)

Ссылки

• Алонсо, Дж. М.; и другие. (1991), «Заметки о гиперболических группах слов», Теория групп с геометрической точки зрения (Триест, 1990) (PDF) , Ривер Эдж, Нью-Джерси: World Scientific, Следствие 3.6, MR   1170363 , заархивировано из оригинала (PDF) в 2013 году. -04-25 , получено 26 ноября 2013 г.
• Олспах, Брайан (1997), «Изоморфизм и графы Кэли на абелевых группах», Симметрия графа (Монреаль, PQ, 1996) , NATO Adv. наук. Инст. Сер. С Математика. Физ. наук, том. 497, Дордрехт: Клювер Акад. Публикация, стр. 1–22, ISBN.  978-0-792-34668-5 , МР   1468786
• Алуффи, Паоло (2009), «6.4 Пример: подгруппы циклических групп», Алгебра, Глава 0 , Аспирантура по математике , том. 104, Американское математическое общество, стр. 82–84, ISBN.  978-0-8218-4781-7
• Бурбаки, Николя (03 августа 1998 г.) [1970], Алгебра I: Главы 1–3 , Элементы математики, том. 1 (переиздание в мягкой обложке), Springer Science & Business Media, ISBN  978-3-540-64243-5
• Коксетер, HSM ; Мозер, WOJ (1980), Генераторы и отношения для дискретных групп , Нью-Йорк: Springer-Verlag, с. 1, ISBN  0-387-09212-9
• Лажуа, Кэролайн; Мура, Роберта (ноябрь 2000 г.), «Что в имени? Трудности в обучении в связи с циклическими группами», For the Learning of Mathematics , 20 (3): 29–33, JSTOR   40248334.
• Кокс, Дэвид А. (2012), Теория Галуа , Чистая и прикладная математика (2-е изд.), John Wiley & Sons, Теорема 11.1.7, стр. 294, номер домена : 10.1002/9781118218457 , ISBN  978-1-118-07205-9
• Галлиан, Джозеф (2010), Современная абстрактная алгебра (7-е изд.), Cengage Learning, Упражнение 43, с. 84, ISBN  978-0-547-16509-7
• Ганнон, Терри (2006), Самогон за пределами монстра: мост, соединяющий алгебру, модульные формы и физику , Кембриджские монографии по математической физике, Cambridge University Press, стр. 18, ISBN  978-0-521-83531-2 , Z _n является простым тогда и только тогда, когда n простое.
• Юнгникель, Дитер (1992), «О уникальности циклической группы порядка n », American Mathematical Monthly , 99 (6): 545–547, doi : 10.2307/2324062 , JSTOR   2324062 , MR   1166004
• Фукс, Ласло (2011), Частично упорядоченные алгебраические системы , Международная серия монографий по чистой и прикладной математике, том. 28, Courier Dover Publications, стр. 28. 63, ISBN  978-0-486-48387-0
• Курцвейл, Ганс; Штелмахер, Бернд (2004), Теория конечных групп: Введение , Universitext, Springer, стр. 50, ISBN  978-0-387-40510-0
• Мотвани, Раджив ; Рагхаван, Прабхакар (1995), Рандомизированные алгоритмы , издательство Кембриджского университета, теорема 14.14, стр. 401, ISBN  978-0-521-47465-8
• Оре, Эйстейн (1938), «Структуры и теория групп. II», Duke Mathematical Journal , 4 (2): 247–269, doi : 10.1215/S0012-7094-38-00419-3 , hdl : 10338.dmlcz/100155 , МР   1546048
• Ротман, Джозеф Дж. (1998), Теория Галуа , Universitytext, Springer, Теорема 62, стр. 65, ISBN  978-0-387-98541-1
• Столлингс, Джон (1970), «Группы когомологического измерения один», Приложения категориальной алгебры (Proc. Sympos. Pure Math., Vol. XVIII, Нью-Йорк, 1968) , Провиденс, Род-Айленд: Amer. Математика. Соц., стр. 124–128, МР   0255689.
• Стюарт, Ян ; Голубицкий, Мартин (2010), Страшная симметрия: является ли Бог геометром? , Courier Dover Publications, стр. 47–48, ISBN.  978-0-486-47758-9
• Вильфред В. (2004), «О циркулянтных графах», Балакришнан, Р.; Сетураман, Г.; Уилсон, Робин Дж. (ред.), Теория графов и ее приложения (Университет Анны, Ченнаи, 14–16 марта 2001 г.) , Alpha Science, стр. 34–36, ISBN  8173195692
• Виноградов, И.М. (2003), «§ VI ПРИМИТИВНЫЕ КОРНИ И ИНДЕКСЫ» , Элементы теории чисел , Минеола, Нью-Йорк: Dover Publications, стр. 105–132, ISBN  0-486-49530-2

Дальнейшее чтение

• Херштейн, IN (1996), Абстрактная алгебра (3-е изд.), Prentice Hall , стр. 53–60, ISBN  978-0-13-374562-7 , МР   1375019

Внешние ссылки

• Милн, Теория групп, http://www.jmilne.org/math/CourseNotes/gt.html.
• Введение в циклические группы
• Вайсштейн, Эрик В. «Циклическая группа» . Математический мир .
• Циклические группы малого порядка по GroupNames
• Любая циклическая группа абелева