Обычная последовательность складывания бумаги

В математике обычная последовательность складывания бумаги , также известная как последовательность кривой дракона , представляет собой бесконечную последовательность нулей и единиц. Он получается из повторяющейся частичной последовательности

1, ?, 0, ?, 1, ?, 0, ?, 1, ?, 0, ?, ...

заполняя знаки вопроса другой копией всей последовательности. Первые несколько членов полученной последовательности:

1, 1, 0, 1, 1, 0, 0, 1, 1, 1, 0, 0, 1, 0, 0, 1, ... (последовательность A014577 в OEIS )

Если полоску бумаги несколько раз сложить пополам в одном и том же направлении, $i$ раз, он получит $2^{i}-1$ складки, направление которых (влево или вправо) задается сочетанием 0 и 1 в первом $2^{i}-1$ с точки зрения обычной последовательности складывания бумаги. Раскрытие каждой складки для создания прямоугольного угла (или, что то же самое, выполнение последовательности поворотов влево и вправо через регулярную сетку, следуя шаблону последовательности складывания бумаги) создает последовательность многоугольных цепочек , которая приближается к фракталу кривой дракона :

1	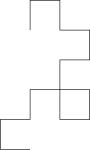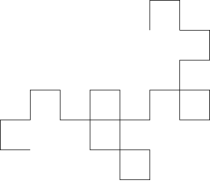1 1 0	1 1 0 1 1 0 0	1 1 0 1 1 0 0 1 1 1 0 0 1 0 0	...

Свойства

Ценность любого данного термина $t_{n}$ в обычной последовательности складывания бумаги, начиная с $n=1$, можно найти рекурсивно следующим образом. Разделять $n$ на два, как можно больше раз, чтобы получить факторизацию формы $n=m\cdot 2^{k}$ где $m$ это нечетное число . Затем

$$t_{n}={\begin{cases}1&{\text{if }}m\equiv 1\mod 4\\0&{\text{if }}m\equiv 3\mod 4\end{cases}}$$

Так, например, $t_{12}=t_{3}=0$: при двойном делении 12 на два остается нечетное число 3. Другой пример: $t_{13}=1$ потому что 13 соответствует 1 по модулю 4.

Слово складывания бумаги 1101100111001001..., которое создается путем объединения членов обычной последовательности складывания бумаги, является фиксированной точкой морфизма или замены строк правил .

11 → 1101

01 → 1001

10 → 1100

00 → 1000

следующее:

11 → 1101 → 11011001 → 1101100111001001 → 11011001110010011101100011001001 ...

Из правил морфизма видно, что слово, складывающееся из бумаги, содержит не более трех последовательных 0 и не более трех последовательных единиц.

Последовательность складывания бумаги также удовлетворяет соотношению симметрии:

$t_{n}={\begin{cases}1&{\text{if }}n=2^{k}\\1-t_{2^{k}-n}&{\text{if }}2^{k-1}<n<2^{k}\end{cases}}$

который показывает, что слово, складывающее бумагу, может быть построено как предел другого итерационного процесса следующим образом:

1

1 1 0

110 1 100

1101100 1 1100100

110110011100100 1 110110001100100

На каждой итерации этого процесса в конце строки предыдущей итерации ставится 1, затем эта строка повторяется в обратном порядке, заменяя 0 на 1 и наоборот.

Генерирующая функция

последовательности Производящая функция складывания бумаги определяется выражением

$G(t_{n};x)=\sum _{n=1}^{\infty }t_{n}x^{n}\,.$

Из построения последовательности складывания бумаги видно, что G удовлетворяет функциональному соотношению

$G(t_{n};x)=G(t_{n};x^{2})+\sum _{n=0}^{\infty }x^{4n+1}=G(t_{n};x^{2})+{\frac {x}{1-x^{4}}}\,.$

Константа складывания бумаги

Подстановка x = 0,5 в производящую функцию дает действительное число от 0 до 1, двоичное представление которого представляет собой слово, складывающееся из бумаги.

$G(t_{n};{\frac {1}{2}})=\sum _{n=1}^{\infty }{\frac {t_{n}}{2^{n}}}$

Это число известно как константа складывания бумаги. и имеет значение

$\sum _{k=0}^{\infty }{\frac {8^{2^{k}}}{2^{2^{k+2}}-1}}=0.85073618820186...$ (последовательность A143347 в OEIS )

Общая последовательность складывания бумаги

Обычная последовательность складывания бумаги соответствует последовательному складыванию полоски бумаги в одном и том же направлении. Если мы позволим направлению складки меняться на каждом шаге, мы получим более общий класс последовательностей. двоичную последовательность ( fi _{Учитывая} ), мы можем определить общую последовательность складывания бумаги с инструкциями по складыванию ( ) _fi .

Для двоичного слова w пусть w ^‡ обозначаем обратную сторону дополнения к w . Определим оператор F _a как

$F_{a}:w\mapsto waw^{\ddagger }\$

а затем определим последовательность слов, зависящую от ( f _i ), посредством w ₀ = ε,

$w_{n}=F_{f_{1}}(F_{f_{2}}(\cdots F_{f_{n}}(\varepsilon )\cdots ))\ .$

Предел w последовательности w _n является последовательностью сворачивания бумаги. Обычная последовательность складывания бумаги соответствует последовательности складывания f _i = 1 для всех i .

Если n = m ·2 ^к где m нечетно, тогда

$t_{n}={\begin{cases}f_{j}&{\text{if }}m\equiv 1\mod 4\\1-f_{j}&{\text{if }}m\equiv 3\mod 4\end{cases}}$

который можно использовать как определение последовательности складывания бумаги.

Свойства

• Последовательность складывания бумаги не является в конечном итоге периодической.
• Последовательность складывания бумаги является 2- автоматической тогда и только тогда, когда последовательность складывания является в конечном счете периодической (1-автоматической).

Ссылки

• Аллуш, Жан-Поль; Шалит, Джеффри (2003). Автоматические последовательности: теория, приложения, обобщения . Издательство Кембриджского университета . ISBN  978-0-521-82332-6 . Збл   1086.11015 .