Жесткое оригами
Жесткое оригами — это ветвь оригами , которая связана со складными конструкциями из плоских жестких листов, соединенных петлями . То есть, в отличие от традиционного оригами, листы бумаги в процессе складывания нельзя сгибать; они должны всегда оставаться плоскими, а бумага должна складываться только по петлям. Жесткая модель оригами по-прежнему могла бы складываться, если бы она была сделана из листов стекла с петлями вместо линий сгиба.
Однако не требуется, чтобы конструкция начиналась с одного плоского листа — например, сумки для покупок с плоским дном изучаются как часть жесткого оригами.
Жесткое оригами является частью изучения математики складывания бумаги , а жесткие структуры оригами можно рассматривать как тип механической связи . Жесткое оригами имеет большую практическую полезность.
Математика
[ редактировать ]Количество стандартных основ оригами , которые можно сложить с помощью жесткого оригами, ограничено его правилами. [1] Жесткое оригами не обязательно должно следовать аксиомам Хузиты-Хатори : линии сгиба можно рассчитать, а не строить из существующих линий и точек. При складывании жесткого плоского оригами теорема Кавасаки и теорема Маекавы ограничивают возможные схемы складывания, как и в обычном оригами, но они больше не дают точной характеристики: некоторые узоры, которые можно сложить плоско в обычном оригами, не могут быть сложены плоско. жестко. [2]
Теорема Беллоуза гласит, что гибкий многогранник имеет постоянный объем при жестком изгибе. [3]
Задача о складывании салфетки состоит в том, можно ли сложить квадрат так, чтобы периметр получившейся плоской фигуры увеличился. Возможность решения этой задачи в рамках жесткого оригами была доказана А.С. Тарасовым в 2004 году. [4]
Раскрытие — это жесткое оригами перемещение развертки многогранника из плоского развернутого состояния в свернутый многогранник или наоборот. Хотя каждый выпуклый многогранник имеет сетку с размытием, неизвестно, существует ли размытие, не пересекающее грани многогранника, или все ли сети выпуклых многогранников имеют размытие. [5]
Теория сложности
[ редактировать ]Определить, можно ли сложить все складки рисунка складок одновременно как часть жесткого оригами или можно сложить подмножество складок, обе задачи являются NP-трудными . Это верно даже для определения существования движения складывания, которое удерживает бумагу сколь угодно близко к ее плоскому состоянию, поэтому (в отличие от других результатов по твердости узоров складных складок оригами) этот результат не основан на невозможности самопересечений. сложенной бумаги. [6]
Приложения
[ редактировать ]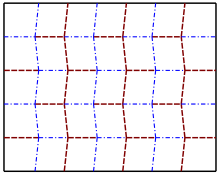
Складка Miura — это жесткая складка, которая использовалась для упаковки больших массивов солнечных батарей для космических спутников, которые необходимо складывать перед развертыванием.
Роберт Дж. Лэнг применил жесткое оригами к задаче складывания космического телескопа. [7]
Хотя бумажные пакеты для покупок обычно складывают плоско, а затем разворачивают, стандартная схема складывания для этого не является жесткой; бока сумки слегка прогибаются в сложенном и разложенном виде. Натяжение бумаги, вызванное этим изгибом, приводит к тому, что она принимает два плоских состояния: плоско сложенный и раскрытый пакет. [8]
Рекреационное использование
[ редактировать ]Мартин Гарднер популяризировал флексагоны , представляющие собой форму жесткого оригами и гибкой трубки. [9]
Калейдоциклы — это игрушки, обычно сделанные из бумаги, которые при скручивании дают эффект, похожий на калейдоскоп.
Ссылки
[ редактировать ]- ^ Демейн, ЭД (2001). Складывание и раскладывание (кандидатская диссертация). Университет Ватерлоо, Канада. hdl : 10012/1068 .
- ^ Авель, Закари; Кантарелла, Джейсон; Демейн, Эрик Д .; Эппштейн, Дэвид ; Халл, Томас С .; Ку, Джейсон С.; Ланг, Роберт Дж .; Тачи, Томохиро (2016). «Жесткие вершины оригами: условия и принудительные множества». Журнал вычислительной геометрии . 7 (1): 171–184. дои : 10.20382/jocg.v7i1a9 . МР 3491092 . S2CID 7181079 .
- ^ Коннелли, Р .; Сабитов И.; Вальц, А. (1997). «Гипотеза о мехах» . Вклад в алгебру и геометрию . 38 (1): 1–10. МР1447981 .
- ^ Тарасов А.С. (2004). «Решение задачи Арнольда о «сложенном рубле»» . Чебышевский сборник . 5 (1): 174–187. Архивировано из оригинала 25 августа 2007 г.
- ^ Миллер, Эзра; Пак, Игорь (2008). «Метрическая комбинаторика выпуклых многогранников: разрезы и непересекающиеся развертки» . Дискретная и вычислительная геометрия . 39 (1–3): 339–388. дои : 10.1007/s00454-008-9052-3 . МР 2383765 . S2CID 10227925 . . Анонсирован в 2003 году.
- ^ Акитая, Хьюго; Демейн, Эрик ; Хорияма, Такаши; Халл, Томас ; Ку, Джейсон; Тачи, Томохиро (2020). «Жесткая складчатость NP-трудна» . Журнал вычислительной геометрии . 11 (1). arXiv : 1812.01160 .
- ^ «Очковый космический телескоп» (PDF) .
- ^ Девин. Дж. Балкком, Эрик Д. Демейн , Мартин Л. Демейн (ноябрь 2004 г.). «Складные бумажные пакеты для покупок» . Тезисы 14-го ежегодного осеннего семинара по вычислительной геометрии . Кембридж, Массачусетс: 14–15.
{{cite journal}}: CS1 maint: несколько имен: список авторов ( ссылка ) - ^ Вайсштейн, Эрик В. «Flexatube» . Вольфрам Математический мир .