Треугольник Пенроуза
Треугольник Пенроуза , также известный как трибар Пенроуза , невозможный трибар . [1] или невозможный треугольник , [2] треугольный — невозможный объект , оптическая иллюзия, состоящая из объекта, который можно изобразить на перспективном рисунке. Он не может существовать как твёрдый объект в обычном трёхмерном евклидовом пространстве, хотя и может быть изометрически вложен в пятимерное евклидово пространство. [3] Впервые его создал шведский художник Оскар Реутерсвард в 1934 году. [4] Независимо от Рейтерсварда, треугольник был разработан и популяризирован в 1950-х годах психиатром Лайонелом Пенроузом и его сыном, математиком и лауреатом Нобелевской премии Роджером Пенроузом , которые описали его как «невозможность в чистом виде». [5] Он занимает видное место в работах художника М. К. Эшера , чьи ранние изображения невозможных объектов отчасти вдохновили его.
Описание
[ редактировать ]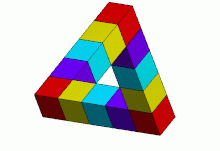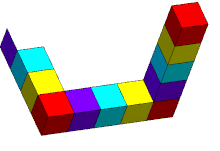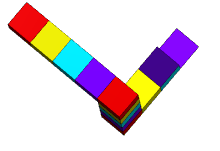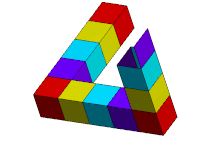
Трибар/треугольник выглядит как твердый объект, состоящий из трех прямых балок квадратного сечения, которые попарно пересекаются под прямым углом в вершинах образуемого ими треугольника . Балки могут ломаться, образуя кубы или кубоиды.
Такое сочетание свойств не может быть реализовано ни одним трехмерным объектом в обычном евклидовом пространстве . Такой объект может существовать в некоторых евклидовых 3-многообразиях , [6] а также может существовать в 5-мерном евклидовом пространстве, [7] которое является евклидовым пространством наименьшей размерности, в которое можно встроить треугольник Пенроуза. Также существуют трехмерные твердые формы, каждая из которых, если смотреть под определенным углом, выглядит так же, как двухмерное изображение треугольника Пенроуза на этой странице (как, например, соседнее изображение, изображающее скульптуру в Перте). , Австралия ). Термин «треугольник Пенроуза» может относиться к двухмерному изображению или самому невозможному объекту.
Если провести линию вокруг треугольника Пенроуза, 4-петлевая лента Мёбиуса . образуется [8]
Изображения
[ редактировать ]
М. К. Эшера « На литографии Водопад » (1961) изображен водоток, который течет зигзагом вдоль длинных сторон двух вытянутых треугольников Пенроуза, так что в конце оказывается на два этажа выше, чем начал. Образовавшийся водопад, образующий короткие стороны обоих треугольников, приводит в движение водяное колесо . Эшер указывает, что для того, чтобы колесо продолжало вращаться, необходимо время от времени добавлять немного воды, чтобы компенсировать испарение .
Скульптуры
[ редактировать ]
Невозможная треугольная скульптура как оптическая иллюзия , Восточный Перт, Западная Австралия
Скульптура «Невозможный треугольник», Готшухен, Австрия.![Настоящий треугольник Пенроуза, нержавеющая сталь, работа WAStanggaßinger, Вассербург-ам-Инн, Германия. Этот тип невозможного треугольника был впервые создан в 1969 году советским художником-кинетиком Вячеславом Колейчуком.[9]](//upload.wikimedia.org/wikipedia/commons/thumb/b/bf/Penrose_Triangle_auf_Ecke_stehend.jpg/240px-Penrose_Triangle_auf_Ecke_stehend.jpg)
Настоящий треугольник Пенроуза, нержавеющая сталь, работа WAStanggaßinger, Вассербург-ам-Инн, Германия. Этот тип невозможного треугольника впервые создал в 1969 году советский художник-кинетик Вячеслав Колейчук . [9]
![Настоящий треугольник Пенроуза, нержавеющая сталь, работа WAStanggaßinger, Вассербург-ам-Инн, Германия. Этот тип невозможного треугольника был впервые создан в 1969 году советским художником-кинетиком Вячеславом Колейчуком.[9]](http://upload.wikimedia.org/wikipedia/commons/thumb/b/bf/Penrose_Triangle_auf_Ecke_stehend.jpg/240px-Penrose_Triangle_auf_Ecke_stehend.jpg)
См. также
[ редактировать ]Ссылки
[ редактировать ]- ^ Паппас, Теони (1989). «Невозможный трибар». Радость математики: открывая для себя математику повсюду . Сан-Карлос, Калифорния: Wide World Publ./Tetra. п. 13.
- ^ Брауэр, Джеймс Р.; Рубин, Дэвид К. (июнь 1979 г.). «Простая конструкция невозможного треугольника». Восприятие . 8 (3): 349–350. дои : 10.1068/p080349 . ПМИД 534162 . S2CID 41895719 .
- ^ https://www.maplesoft.com/mapleconference/resources/54_Zeng_IsometricEmbedding_slides.pdf
- ^ Эрнст, Бруно (1986). «Невозможная фигура Эшера печатается в новом контексте». В Кокстере, HSM ; Эммер, М.; Пенроуз, Р .; Тойбер, М.Л. (ред.). Искусство и наука М.К. Эшера: материалы Международного конгресса по М.К. Эшеру, Рим, Италия, 26–28 марта 1985 г. Северная Голландия. стр. 125–134. См., в частности, стр. 131.
- ^ Пенроуз, Лос-Анджелес ; Пенроуз, Р. (февраль 1958 г.). «Невозможные объекты: особый вид зрительной иллюзии». Британский журнал психологии . 49 (1): 31–33. дои : 10.1111/j.2044-8295.1958.tb00634.x . ПМИД 13536303 .
- ^ Фрэнсис, Джордж К. (1988). «Глава 4: Невозможный трибар». Топологическая книжка с картинками . Спрингер. стр. 65–76. дои : 10.1007/978-0-387-68120-7_4 . ISBN 0-387-96426-6 . См., в частности, стр. 68, где Фрэнсис приписывает это наблюдение Джону Стиллвеллу .
- ^ https://www.maplesoft.com/mapleconference/resources/54_Zeng_IsometricEmbedding_slides.pdf
- ^ Гарднер, Мартин (август 1978 г.). «Математические игры: лента Мёбиуса имеет конечную толщину, поэтому на самом деле это скрученная призма». Научный американец . 239 (2): 18–26. дои : 10.1038/scientificamerican1278-18 . JSTOR 24960346 .
- ^ Федоров, Ю. (1972). "Невозможное-Возможно" . Техника Молодежи . 4 : 20–21.
