Красно-черное дерево

Красно-черное дерево
Тип	Дерево
Изобретенный	1978
Изобретён	Леонидас Дж. Гибас и Роберт Седжвик
Сложности в обозначении большого О
Пространственная сложность Космос $O(n)$ Временная сложность Функция Амортизированный Худший случай Поиск $O(\log n)$ $O(\log n)$ Вставлять $O(\log n)$ $O(\log n)$ Удалить $O(\log n)$ $O(\log n)$

В информатике красно -черное дерево представляет собой самобалансирующуюся структуру данных двоичного дерева поиска , отличающуюся быстрым хранением и поиском упорядоченной информации. Узлы красно-черного дерева содержат дополнительный бит «цвета», часто изображаемый красным и черным, что помогает гарантировать, что дерево всегда приблизительно сбалансировано.

Когда дерево модифицируется, новое дерево перестраивается и «перекрашивается», чтобы восстановить свойства окраски, которые ограничивают то, насколько несбалансированным дерево может стать в худшем случае. Свойства спроектированы таким образом, чтобы такую ​​перестановку и перекрашивание можно было выполнять эффективно.

(Ре)балансировка не идеальна, но гарантирует поиск в $O(\log n)$ время, где $n$ количество записей в дереве. Операции вставки и удаления, а также перестановка и перекрашивание дерева также выполняются в $O(\log n)$ время.

Для отслеживания цвета каждого узла требуется только один бит информации на узел, поскольку цветов всего два (из-за выравнивания памяти, присутствующего в некоторых языках программирования, реальное потребление памяти может отличаться). Дерево не содержит никаких других данных, характерных для того, что оно является красно-черным деревом, поэтому его объем памяти почти идентичен объему памяти классического (неокрашенного) двоичного дерева поиска . В некоторых случаях добавленный бит информации может быть сохранен без дополнительных затрат памяти.

История

В 1972 году Рудольф Байер изобрел структуру данных, которая представляла собой особый случай B-дерева четвертого порядка . Эти деревья поддерживали все пути от корня к листу с одинаковым количеством узлов, создавая идеально сбалансированные деревья. Однако это не были двоичные деревья поиска. В своей статье Байер назвал их «симметричным бинарным B-деревом», а позже они стали популярны как 2–3–4 дерева или даже 2–3 дерева.

В статье 1978 года «Двуцветный каркас для сбалансированных деревьев» Леонидас Дж. Гибас и Роберт Седжвик вывели красно-черное дерево из симметричного двоичного B-дерева. Цвет «красный» был выбран потому, что это был самый красивый цвет, полученный на цветном лазерном принтере, доступном авторам во время работы в Xerox PARC . В другом ответе Гибаса говорится, что это произошло из-за красных и черных ручек, которыми они могли рисовать деревья.

В 1993 году Арне Андерссон представил идею наклоненного вправо дерева для упрощения операций вставки и удаления.

В 1999 году Крис Окасаки показал, как сделать операцию вставки чисто функциональной. Его функция баланса должна была обрабатывать только 4 несбалансированных случая и один сбалансированный случай по умолчанию.

Исходный алгоритм использовал 8 несбалансированных случаев, но Кормен и др. (2001) сократили это число до 6 несбалансированных случаев. Седжвик показал, что операцию вставки можно реализовать всего за 46 строк Java- кода. В 2008 году Седжвик предложил красно-черное дерево, наклоненное влево , используя идею Андерссона, упрощающую операции вставки и удаления. Первоначально Седжвик допускал узлы, у которых два дочерних элемента красные, что делало его деревья больше похожими на 2–3–4 дерева, но позже это ограничение было добавлено, и новые деревья стали больше похожи на 2–3 дерева. Седжвик реализовал алгоритм вставки всего за 33 строки, значительно сократив исходные 46 строк кода.

Терминология

Пример красно-черного дерева

Рисунок 1: ... с явными выходами NIL

Рисунок 2: ... с неявными левой и правой точками стыковки

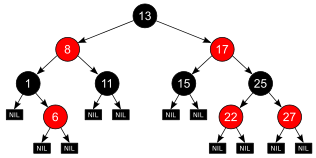
Красно-черное дерево — это особый тип двоичного дерева поиска , используемый в информатике для организации частей сопоставимых данных , таких как фрагменты текста или числа (например, числа на рисунках 1 и 2). Узлы, несущие ключи и/или данные, часто называются «внутренними узлами» , но для большей конкретики в этой статье их также называют узлами, отличными от NIL.

Листовые узлы красно-черных деревьев (   NIL   на рисунке 1) не содержат ключей или данных. Эти «листья» не обязательно должны быть явными отдельными личностями в памяти компьютера: NULL-указатель может, как и во всех структурах данных двоичного дерева, кодировать тот факт, что в этой позиции в (родительском) узле нет дочернего узла. Тем не менее, по своему положению в дереве эти объекты находятся по отношению к другим узлам, что соответствует RB-структуре: у них может быть родительский, одноуровневый (т. е. другой дочерний элемент родителя), дядя и даже племянник узла; и может быть дочерним, но никогда родительским, другого узла. На самом деле нет необходимости приписывать «цвет» этим объектам конца пути, поскольку условие «является NIL или BLACK" подразумевается условием "является NIL(см. также это замечание ).

На рисунке 2 показано концептуально такое же красно-черное дерево без этих NIL-листьев. Чтобы прийти к такому же понятию пути , нужно заметить, что, например, через узел 1 проходят 3 пути , а именно путь через 1 _левый плюс 2 добавленных пути через 1 _правый , а именно пути через 6 _левый и 6 _правый . Таким образом, эти концы путей также являются точками стыковки для вставки новых узлов, что полностью эквивалентно NIL-листьям на рисунке 1.

Вместо этого, чтобы сэкономить незначительное время выполнения, эти (возможно, многие) NIL-листы могут быть реализованы как указатели на один уникальный (и черный) сторожевой узел (вместо указателей со значением NULL ).

В заключение следует отметить, что тот факт, что дочерний узел не существует (не является истинным узлом, не содержит данных), во всех случаях может быть указан тем же самым NULL-указателем или тем же указателем на дозорный узел. В этой статье любой вариант называется узлом NIL и имеет постоянное значение. NIL.

Глубина черного узла определяется как количество черных узлов от корня до этого узла (т. е. количество черных предков). Высота черного красно-черного дерева — это количество черных узлов на любом пути от корня к листьям, которое по требованию 4 является постоянным (альтернативно его можно определить как глубину черного любого листового узла). Черная высота узла — это черная высота поддерева, корнем которого он является. В этой статье высота черного узла NIL должна быть установлена ​​равной 0, поскольку его поддерево пусто, как показано на рисунке 2, и высота его дерева также равна 0.

Характеристики

Помимо требований, предъявляемых к бинарному дереву поиска, красно-черное дерево должно удовлетворять следующим :

1. Каждый узел либо красный, либо черный.
2. Все узлы NIL (рис. 1) считаются черными.
3. Красный узел не имеет красного дочернего узла.
4. Каждый путь от данного узла к любому из его потомков NIL-узлов проходит через одинаковое количество черных узлов.
5. (Вывод) Если у узла N есть ровно один дочерний узел, он должен быть красным дочерним элементом, потому что, если бы он был черным, его NIL-потомки располагались бы на другой глубине черного, чем N NIL-потомок , что нарушает требование 4 .

Некоторые авторы, например Кормен и др., заявить, что «корень черный» в качестве пятого требования; но не Мельхорн и Сандерс или Седжвик и Уэйн. Поскольку корень всегда можно изменить с красного на черный, это правило мало влияет на анализ. В этой статье он также опущен, поскольку он несколько нарушает рекурсивные алгоритмы и доказательства.

Например, каждое идеальное двоичное дерево , состоящее только из черных узлов, является красно-черным деревом.

Операции только для чтения, такие как поиск или обход дерева, не влияют ни на какие требования. Напротив, изменяющие операции вставки и удаления легко поддерживают требования 1 и 2, но в отношении других требований необходимо приложить некоторые дополнительные усилия, чтобы избежать нарушения требования 3, называемого красным нарушением , или требования 4. называется черным нарушением .

Требования реализуют важнейшее свойство красно-черных деревьев: путь от корня до самого дальнего листа не более чем в два раза длиннее пути от корня до ближайшего листа . В результате дерево сбалансировано по высоте . Поскольку такие операции, как вставка, удаление и поиск значений, в худшем случае требуют времени, пропорционального высоте $h$ дерева, эта верхняя граница высоты позволяет красно-черным деревьям быть эффективными в худшем случае, а именно логарифмическим по числу $n$ записей, т.е. $h\in O(\log n)$, что не относится к обычным двоичным деревьям поиска . Математическое доказательство см. в разделе « Доказательство границ» .

Красно-черные деревья, как и все двоичные деревья поиска , допускают довольно эффективный последовательный доступ (например, обход по порядку , то есть: в порядке Левый-Корневой-Правый) к своим элементам. Но они также поддерживают асимптотически оптимальный прямой доступ посредством обхода от корня к листу, что приводит к $O(\log n)$ время поиска.

Аналогия с 2–3–4 деревьями.

Рисунок 3. Сходства между деревьями 2–3–4 и красно-черными деревьями.

Красно-черные деревья по структуре аналогичны деревьям 2–3–4 , которые являются B-деревьями 4-го порядка. В деревьях 2–3–4 каждый узел может содержать от 1 до 3 значений и иметь от 2 до 4 дочерних элементов. Эти 2–3–4 узла соответствуют черным узлам — красным дочерним группам в красно-черных деревьях, как показано на рисунке 3. Это не соответствие 1 к 1 , поскольку 3-узлы имеют два эквивалентных представления: красный дочерний элемент. может лежать как слева, так и справа. Вариант красно-черного дерева с наклоном влево делает это соотношение точно 1 к 1, допуская только левое дочернее представление. Поскольку каждому узлу 2–3–4 соответствует черный узел, инвариант 4 красно-черных деревьев эквивалентен утверждению, что все листья дерева 2–3–4 лежат на одном уровне.

Несмотря на структурное сходство, операции с красно-черными деревьями более экономичны, чем с B-деревьями. B-деревья требуют управления векторами переменной длины, тогда как красно-черные деревья являются просто бинарными деревьями.

Приложения и связанные структуры данных

Красно-черные деревья предлагают гарантии наихудшего случая для времени вставки, времени удаления и времени поиска. Это не только делает их ценными в чувствительных ко времени приложениях, таких как приложения реального времени , но и делает их ценными строительными блоками в других структурах данных, которые обеспечивают гарантии наихудшего случая. Например, многие структуры данных, используемые в вычислительной геометрии , основаны на красно-черных деревьях, а планировщик Completely Fair и epoll системный вызов ядра Linux используют красно-черные деревья. Дерево AVL — это еще одна структура, поддерживающая $O(\log n)$ поиск, вставка и удаление. Деревья AVL могут быть окрашены в красно-черный цвет и, таким образом, являются подмножеством красно-черных деревьев. Высота AVL в худшем случае в 0,720 раза превышает высоту красно-черных деревьев в худшем случае, поэтому деревья AVL более жестко сбалансированы. Измерения производительности Бена Пфаффа с реалистичными тестовыми примерами в 79 запусках показывают, что соотношение AVL и RB находится между 0,677 и 1,077, медиана 0,947 и среднее геометрическое 0,910. Производительность деревьев WAVL находится между деревьями AVL и красно-черными деревьями.

Красно-черные деревья также особенно ценны в функциональном программировании , где они являются одной из наиболее распространенных постоянных структур данных , используемых для построения ассоциативных массивов и наборов , которые могут сохранять предыдущие версии после мутаций. Постоянная версия красно-черных деревьев требует $O(\log n)$ пространство для каждой вставки или удаления, а также время.

Для каждого дерева 2–3–4 существуют соответствующие красно-черные деревья с элементами данных в том же порядке. Операции вставки и удаления в деревьях 2–3–4 также эквивалентны переворачиванию цветов и вращениям в красно-черных деревьях. Это делает деревья 2–3–4 важным инструментом для понимания логики красно-черных деревьев, и именно поэтому во многих текстах вводных алгоритмов деревья 2–3–4 вводятся непосредственно перед красно-черными деревьями, хотя 2–3–4 деревья не часто используются на практике.

В 2008 году Седжвик представил более простую версию красно-черного дерева, названную красно-черным деревом, наклоненным влево. за счет устранения ранее неуказанной степени свободы в реализации. LLRB поддерживает дополнительный инвариант, согласно которому все красные ссылки должны быть наклонены влево, за исключением случаев вставки и удаления. Красно-черные деревья можно сделать изометричными либо 2–3 деревьям , либо 2–3 деревьям. или 2–3–4 дерева, для любой последовательности операций. Изометрия дерева 2–3–4 была описана в 1978 году Седжвиком. При наличии 2–3–4 деревьев изометрия разрешается путем «переворота цвета», соответствующего разделению, при котором красный цвет двух дочерних узлов покидает дочерние узлы и перемещается к родительскому узлу.

Исходное описание дерева танго , типа дерева, оптимизированного для быстрого поиска, специально использует красно-черные деревья как часть своей структуры данных.

Начиная с Java 8, HashMap был изменен таким образом, что вместо использования LinkedList для хранения различных элементов с конфликтующими хэш-кодами используется красно-черное дерево. Это приводит к улучшению временной сложности поиска такого элемента из $O(m)$ к $O(\log m)$ где $m$ — количество элементов с конфликтующими хэш-кодами.

Операции

Операции только для чтения, такие как поиск или обход дерева, на красно-черном дереве не требуют изменений по сравнению с теми, которые используются для двоичных деревьев поиска , поскольку каждое красно-черное дерево является особым случаем простого двоичного дерева поиска. Однако непосредственный результат вставки или удаления может нарушить свойства красно-черного дерева, восстановление которого называется ребалансировкой, так что красно-черные деревья становятся самобалансирующими. потребуется В худшем случае для этого небольшое количество, $O(\log n)$ в обозначении Big O , где $n$ количество объектов в дереве, среднее или амортизированное $O(1)$, постоянное число, изменений цвета (которые на практике происходят очень быстро); и не более трех вращений дерева (два для вставки).

Если приведенный ниже пример реализации не подходит, другие реализации с пояснениями можно найти в книге Бена Пфаффа. аннотированная библиотека C GNU libavl (v2.0.3 по состоянию на июнь 2019 г.).

Подробности операций вставки и удаления будут продемонстрированы на примере кода C++ , в котором используются определения типов, макросы ниже и вспомогательная функция для вращения:

// Basic type definitions:

enum color_t { BLACK, RED };

struct RBnode {     // node of red–black tree
  RBnode* parent;   // == NIL if root of the tree
  RBnode* child[2]; // == NIL if child is empty
    // The index is:
    //   LEFT  := 0, if (key < parent->key)
    //   RIGHT := 1, if (key > parent->key)
  enum color_t color;
  int key;
};

#define NIL   NULL // null pointer  or  pointer to sentinel node
#define LEFT  0
#define RIGHT 1
#define left  child[LEFT]
#define right child[RIGHT]

struct RBtree { // red–black tree
  RBnode* root; // == NIL if tree is empty
};

// Get the child direction (∈ { LEFT, RIGHT })
//   of the non-root non-NIL  RBnode* N:
#define childDir(N) ( N == (N->parent)->right ? RIGHT : LEFT )

Левое вращение и
правое вращение, анимация.

RBnode* RotateDirRoot(
    RBtree* T,   // red–black tree
    RBnode* P,   // root of subtree (may be the root of T)
    int dir) {   // dir ∈ { LEFT, RIGHT }
  RBnode* G = P->parent;
  RBnode* S = P->child[1-dir];
  RBnode* C;
  assert(S != NIL); // pointer to true node required
  C = S->child[dir];
  P->child[1-dir] = C; if (C != NIL) C->parent = P;
  S->child[  dir] = P; P->parent = S;
  S->parent = G;
  if (G != NULL)
    G->child[ P == G->right ? RIGHT : LEFT ] = S;
  else
    T->root = S;
  return S; // new root of subtree
}

#define RotateDir(N,dir) RotateDirRoot(T,N,dir)
#define RotateLeft(N)    RotateDirRoot(T,N,LEFT)
#define RotateRight(N)   RotateDirRoot(T,N,RIGHT)

Примечания к примеру кода и схемам установки и удаления.

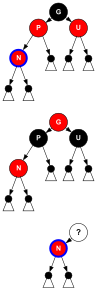
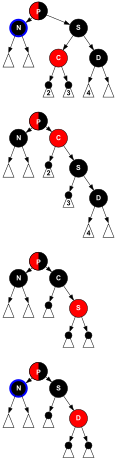
В предложении как вставка, так и удаление (не говоря уже о некоторых очень простых случаях) разбивается на шесть созвездий узлов, ребер и цветов, которые называются случаями. Предложение содержит как для вставки, так и для удаления ровно один случай, который приближает один уровень черного ближе к корню и зацикливает, остальные пять случаев самостоятельно перебалансируют дерево. Более сложные случаи изображены на схеме.

• символизирует красный узел и черный узел (не NIL) (высота черного ≥ 1), символизирует красный или черный цвет узла, отличного от NIL, но один и тот же цвет на всей диаграмме. NIL-узлы на диаграммах не представлены.
• Переменная N обозначается   N   или   N.   обозначает текущий узел, который на диаграммах
• Диаграмма содержит три столбца и от двух до четырех действий. Левый столбец показывает первую итерацию, правый столбец — более высокие итерации, средний столбец показывает сегментацию случая на различные действия.

1. Действие «запись» показывает совокупность узлов с их цветами, что определяет случай и в большинстве случаев нарушает некоторые требования .
   Синяя рамка окружает текущий узел N а остальные узлы помечены в соответствии с их отношением к N. ,
2. Если вращение считается полезным, это отображается в следующем действии, которое называется «вращение».
3. Если какое-то перекрашивание считается полезным, это отображается в следующем действии, которое называется «Цвет».
4. Если все еще существует необходимость в ремонте, в случаях используется код других случаев, и это после переназначения текущего узла N , который затем снова несет синее кольцо и относительно которого, возможно, придется переназначить и другие узлы. Это действие называется «переназначить».
   И для вставки, и для удаления существует (ровно) один случай, который повторяет один уровень черного ближе к корню; тогда переназначенное созвездие удовлетворяет соответствующему инварианту цикла.

• Возможно, пронумерованный треугольник с черным кругом наверху. представляет красно-черное поддерево (соединенное со своим родителем согласно требованию 3 ) с высотой черного цвета, равной уровню итерации минус единица, т.е. нулю в первой итерации. Его корень может быть красным или черным.
  Возможно пронумерованный треугольник представляет красно-черное поддерево с высотой черного цвета на единицу меньше, т.е. его родительский элемент имеет нулевую высоту черного цвета на второй итерации.

Примечание

Для простоты в примере кода используется дизъюнкция :

U == NIL || U->color == BLACK // considered black

и союз :

U != NIL && U->color == RED   // not considered black

При этом следует иметь в виду, что оба утверждения не оцениваются в совокупности, если U == NIL. Тогда в обоих случаях U->color не трогается (см. Оценка короткого замыкания ).
(Комментарий considered black соответствует требованию 2 .)

Соответствующие if-высказывания должны повторяться гораздо реже, если предложение реализуется.

Вставка

Вставка начинается с помещения нового (не NIL) узла, скажем N , в позицию в двоичном дереве поиска узла NIL, чей предшествующий ключ по порядку сравнивается меньше, чем ключ нового узла, который, в свою очередь, сравнивается меньше, чем ключ. своего нормального преемника. (Часто такое расположение является результатом поиска внутри дерева, непосредственно предшествующего операции вставки, и состоит из узла P вместе с направлением dir с P->child[dir] == NIL.) Вновь вставленный узел временно окрашивается в красный цвет, чтобы все пути содержали то же количество черных узлов, что и раньше. Но если его родительский элемент, скажем P , также красный, то это действие приводит к нарушению красного цвета .

void RBinsert1(
  RBtree* T,         // -> red–black tree
  struct RBnode* N,  // -> node to be inserted
  struct RBnode* P,  // -> parent node of N ( may be NULL )
  int dir)           // side ( LEFT or RIGHT ) of P where to insert N
{
  struct RBnode* G;  // -> parent node of P
  struct RBnode* U;  // -> uncle of N

  N->color = RED;
  N->left  = NIL;
  N->right = NIL;
  N->parent = P;
  if (P == NULL) {   // There is no parent
    T->root = N;     // N is the new root of the tree T.
    return; // insertion complete
  }
  P->child[dir] = N; // insert N as dir-child of P
  // start of the (do while)-loop:
  do {

Цикл ребалансировки операции вставки имеет следующий инвариант :

• Переменная N , представляющая текущий узел N и первоначально узел вставки, становится переменной, проходящей через цикл.
• N есть (красный) в начале каждой итерации.
• Требование 3 удовлетворяется для всех пар node ←parent с возможным исключением N ← P , когда P также красный ( нарушение красного цвета в N ).
• Все остальные свойства (включая требование 4 ) удовлетворяются во всем дереве.

Примечания к диаграммам вставок

до

случай

много- ция

назначать напоминание

после

следующий

Δh

П

Г

В

х

П

Г

В

х

я1

✓

я2

Н := Г

?

?

2

—

я3

✓

—

я4

✓

я

I5

P ↶ N

Н := П

тот

I6

0

тот

I6

P ↷ G

✓

Вставка: В предшествующих колонках этого обзора показано, что все возможные случаи созвездий покрыты.

• На диаграммах P используется для G обозначения родителя N, для его дедушки и бабушки, а U для его дяди. В таблице знак — обозначает корень.
• На диаграммах родительский узел P показан как левый дочерний элемент своего родительского узла G, может хотя P находиться с любой стороны. Пример кода охватывает обе возможности с помощью боковой переменной. dir.
• На диаграммах показаны случаи, когда P также красный, нарушение красного цвета.
• Столбец x указывает изменение дочернего направления, т.е. o (для «внешнего») означает, что P и N оба являются левыми или правыми дочерними элементами, тогда как i (для «внутреннего») означает, что дочернее направление меняется с P на Н. ​
• определяет группа столбцов Предыдущая регистр, имя которого указано в столбце case . При этом возможные значения в ячейках, оставленных пустыми, игнорируются. Таким образом, в случае I2 пример кода охватывает обе возможности дочерних направлений N , хотя на соответствующей диаграмме показано только одно.
• Строки в синопсисе упорядочены таким образом, чтобы можно было легко понять все возможные случаи РБ.
• столбца Ротация указывает, способствует ли ротация ребалансировке.
• столбца Назначение показывает присвоение N перед переходом к следующему шагу. повлечет за собой переназначение других узлов P , G , U. Возможно, это также
• Если что-то было изменено по делу, это отображается в группе столбцов после .
• Знак ✓ в следующем столбце означает, что ребалансировка завершена на этом этапе. Если столбец после определяет ровно один случай, этот случай указывается как последующий, в противном случае стоят вопросительные знаки.
• Цикл содержится в разделах «Вставка случая I1» и «Вставка случая I2» , где в случае I2 обостряется проблема ребалансировки. $\Delta h=2$ дерева или на 1 уровень черного выше в дереве, при этом дедушка G становится новым текущим узлом N. уровней Поэтому требуется максимально ${\tfrac {h}{2}}$ шаги итерации по восстановлению дерева (где $h$ — высота дерева). Поскольку вероятность эскалации уменьшается экспоненциально с каждым шагом, общие затраты на ребалансировку в среднем являются постоянными, фактически амортизируемыми постоянными .
• Из тела цикла случай I1 выходит сам по себе и имеются выходные ветви к случаям I4 , I6 , I5 + I6 и I3 .
• Вращения происходят в случаях I6 и I5+I6 – вне цикла. Следовательно, всего происходит не более двух вращений.

Корпус вставки I1

текущего узла Родитель P черный, поэтому требование 3 выполняется. Требование 4 выполняется также в соответствии с инвариантом цикла .

    if (P->color == BLACK) {
      // Case_I1 (P black):
      return; // insertion complete
    }
    // From now on P is red.
    if ((G = P->parent) == NULL) 
      goto Case_I4; // P red and root
    // else: P red and G!=NULL.
    dir = childDir(P); // the side of parent G on which node P is located
    U = G->child[1-dir]; // uncle
    if (U == NIL || U->color == BLACK) // considered black
      goto Case_I56; // P red && U black

Корпус вставки I2

первая итерация

более высокая итерация

Корпус вставки I2

Если и родительский P , и дядя U красные, то их обоих можно перекрасить в черный цвет, а родительский G станет красным для соблюдения требования 4 . Поскольку любой путь через родителя или дядюшку должен проходить через дедушку и бабушку, количество черных узлов на этих путях не изменилось. Однако дедушка G теперь может нарушить требование 3, если у него есть красный родительский элемент. После перемаркировки G на N выполняется инвариант цикла , так что ребалансировку можно повторить на один уровень черного (= 2 уровня дерева) выше.

    // Case_I2 (P+U red):
    P->color = BLACK;
    U->color = BLACK;
    G->color = RED;
    N = G; // new current node
    // iterate 1 black level higher
    //   (= 2 tree levels)
  } while ((P = N->parent) != NULL);
  // end of the (do while)-loop

Корпус вставки I3

Случай вставки I2 был выполнен в течение ${\tfrac {h-1}{2}}$ раз, а общая высота дерева увеличилась на 1 и теперь составляет $h~.$ Текущий узел N является (красным) корнем дерева, и все свойства RB соблюдены.

  // Leaving the (do while)-loop (after having fallen through from Case_I2).
  // Case_I3: N is the root and red.
  return; // insertion complete

Вкладной корпус I4

Родитель P красный и является корнем. Поскольку N также красный, требование 3 нарушается. Но после переключения цвета P дерево принимает форму RB. Высота черного дерева увеличивается на 1.

Case_I4: // P is the root and red:
  P->color = BLACK;
  return; // insertion complete

Вкладной корпус I5

первая итерация

более высокая итерация

Вкладной корпус I5

Родитель P красный, а дядя U черный. Конечная цель состоит в том, чтобы повернуть родительский узел P в положение прародителя, но это не сработает, если N является «внутренним» внуком узла G (т. е. если N является левым дочерним элементом правого дочернего элемента G или правым дочерним элементом узла G). левый ребенок G ). А dir-поворот в точке P переключает роли текущего узла N и его родительского P. узла Вращение добавляет пути через N (те, что в поддереве с меткой 2 , см. диаграмму) и удаляет пути через P (те, что в поддереве с меткой 4 ). Но и P , и N красные, поэтому требование 4 сохраняется. Требование 3 восстанавливается в случае 6.

Case_I56: // P red && U black:
  if (N == P->child[1-dir])
  { // Case_I5 (P red && U black && N inner grandchild of G):
    RotateDir(P,dir); // P is never the root
    N = P; // new current node
    P = G->child[dir]; // new parent of N
    // fall through to Case_I6
  }

Вкладной корпус I6

первая итерация

более высокая итерация

Вкладной корпус I6

Текущий узел N теперь наверняка является «внешним» внуком узла G (слева от левого дочернего узла или справа от правого дочернего узла). Сейчас (1-dir)-повернуть в G , поместив P вместо G и сделав родительским для N и G. P G — черный, а его бывший дочерний элемент P — красный, поскольку требование 3 было нарушено. После переключения цветов P и G полученное дерево удовлетворяет требованию 3. Требование 4 также остается удовлетворенным, поскольку все пути, проходившие через черный G, проходят через черный P. теперь

  // Case_I6 (P red && U black && N outer grandchild of G):
  RotateDirRoot(T,G,1-dir); // G may be the root
  P->color = BLACK;
  G->color = RED;
  return; // insertion complete
} // end of RBinsert1

Поскольку алгоритм преобразует входные данные без использования вспомогательной структуры данных и использует лишь небольшой объем дополнительного пространства для хранения вспомогательных переменных, он находится на месте .

Удаление

Простые случаи

- Когда у удаленного узла есть 2 дочерних узла (не NIL), мы можем поменять его значение на его преемника по порядку (самый левый дочерний элемент правого поддерева), а затем вместо этого удалить преемника. Поскольку преемник является крайним левым, он может иметь только правого дочернего элемента (не NIL) или вообще не иметь дочернего элемента.

- Когда удаленный узел имеет только 1 дочерний элемент (не NIL). В этом случае просто замените узел его дочерним элементом и раскрасьте его в черный цвет.
Единственный дочерний узел (не NIL) должен быть красным согласно выводу 5 , а удаленный узел должен быть черным согласно требованию 3 .

- Если удаленный узел не имеет дочерних элементов (оба NIL) и является корневым, замените его на NIL. Дерево пусто.

- Если удаленный узел не имеет дочерних элементов (оба NIL) и имеет красный цвет , просто удалите листовой узел.

- Если удаленный узел не имеет дочерних элементов (оба NIL) и имеет черный цвет , его удаление создаст дисбаланс и потребует исправления, как описано в следующем разделе.

Удаление черного некорневого листа

Сложный случай — это когда N не является корнем, окрашен в черный цвет и не имеет собственного дочернего элемента (⇔ только дочерние элементы NIL). В первой итерации N заменяется на NIL.

void RBdelete2(
  RBtree* T,         // -> red–black tree
  struct RBnode* N)  // -> node to be deleted
 {
  struct RBnode* P = N->parent;  // -> parent node of N
  byte dir;          // side of P on which N is located (∈ { LEFT, RIGHT })
  struct RBnode* S;  // -> sibling of N
  struct RBnode* C;  // -> close   nephew
  struct RBnode* D;  // -> distant nephew

  // P != NULL, since N is not the root.
  dir = childDir(N); // side of parent P on which the node N is located
  // Replace N at its parent P by NIL:
  P->child[dir] = NIL;
  goto Start_D;      // jump into the loop

  // start of the (do while)-loop:
  do {
    dir = childDir(N);   // side of parent P on which node N is located
Start_D:
    S = P->child[1-dir]; // sibling of N (has black height >= 1)
    D = S->child[1-dir]; // distant nephew
    C = S->child[  dir]; // close   nephew
    if (S->color == RED)
      goto Case_D3;                  // S red ===> P+C+D black
    // S is black:
    if (D != NIL && D->color == RED) // not considered black
      goto Case_D6;                  // D red && S black
    if (C != NIL && C->color == RED) // not considered black
      goto Case_D5;                  // C red && S+D black
    // Here both nephews are == NIL (first iteration) or black (later).
    if (P->color == RED)
      goto Case_D4;                  // P red && C+S+D black

Цикл ребалансировки операции удаления имеет следующий инвариант :

• В начале каждой итерации высота черного цвета N равна номеру итерации минус один, что означает, что в первой итерации она равна нулю и что N является истинно черным узлом. в более высоких итерациях.
• Число черных узлов на путях через N на единицу меньше, чем до удаления, тогда как на всех остальных путях оно не меняется, так что существует нарушение черного цвета, в P если существуют другие пути.
• Все остальные свойства (включая требование 3 ) удовлетворяются во всем дереве.

Примечания к диаграммам удаления

до

случай

много- ция

назначать напоминание

после

следующий

Δh

П

С

С

Д

П

С

С

Д

—

Д1

✓

Д2

Н := П

?

?

1

Д3

P ↶ S

Н := Н

Д6

0

Д5

0

Д4

0

Д4

✓

Д5

C ↷ S

Н := Н

Д6

0

Д6

P ↶ S

✓

Удаление: в предыдущих колонках этого обзора показано, что все возможные случаи цветных созвездий покрыты.

• На диаграммах ниже P используется для N родителя , S для брата и сестры N , C (означает близкого племянника) для ребенка S в том же направлении, что и N , и D (означает дальнего племянника) для S. обозначения другой дочерний элемент ( S не может быть узлом NIL в первой итерации, поскольку он должен иметь высоту черного цвета единицу, которая была высотой черного цвета N до его удаления, но C и D могут быть узлами NIL).
• На диаграммах текущий узел N показан как левый дочерний элемент своего родительского узла P, может хотя N находиться с любой стороны. Примеры кода охватывают обе возможности с помощью боковой переменной. dir.
• В начале (на первой итерации) удаления N — это NIL-узел, заменяющий удаляемый узел. Поскольку его расположение в родительском узле является единственным важным моментом, оно обозначается символом (это означает: текущий узел N является узлом NIL и левым дочерним элементом) в левом столбце диаграмм удаления. По ходу операции также могут стать текущими собственные узлы (высоты черного цвета ≥ 1) (см., например, случай D2 ).
• Считая черные пули ( и ) на диаграмме удаления можно заметить, что пути через N имеют на один маркер меньше, чем другие пути. Это означает нарушение черного цвета в точке P — если оно существует.
• Созвездие цветов в группе столбцов ранее определяет регистр, имя которого указано в столбце case . При этом возможные значения в ячейках, оставленных пустыми, игнорируются.
• Строки в синопсисе упорядочены таким образом, чтобы можно было легко понять все возможные случаи РБ.
• столбца Ротация указывает, способствует ли ротация ребалансировке.
• столбца Назначение показывает присвоение N перед переходом к следующему шагу итерации. повлечет за собой переназначение других узлов P , C , S , D. Это, возможно, также
• Если что-то было изменено по делу, это отображается в группе столбцов после .
• Знак ✓ в следующем столбце означает, что ребалансировка завершена на этом этапе. Если столбец после определяет ровно один случай, этот случай указывается как последующий, в противном случае стоят вопросительные знаки.
• Цикл содержится в разделах из Start_D через «Удалить кейс D2» , где обостряется проблема ребалансировки $\Delta h=1$ уровень выше в дереве, поскольку родительский становится новым текущим узлом N. P Поэтому требуется максимально $h$ итераций по восстановлению дерева (где $h$ — высота дерева). Поскольку вероятность эскалации уменьшается экспоненциально с каждой итерацией, общие затраты на ребалансировку в среднем являются постоянными, фактически амортизируемыми постоянными . (Кстати: Мельхорн и Сандерс отмечают: «Деревья AVL не поддерживают постоянные амортизированные затраты на обновление». Это справедливо для ребалансировки после удаления, но не для вставки AVL. )
• Из тела цикла выходят ветки к случаям D3 , D6 , D5+D6 , D4 и D1 ; Раздел «Удалить кейс D3» сам по себе имеет три разные исходящие ветви к кейсам D6 , D5 и D4 .
• Ротации происходят в случаях D6 и D5+D6 и D3+D5+D6 – все вне цикла. Таким образом, всего происходит не более трех вращений.

Удалить дело D1

Текущий узел N является новым корнем. Из каждого пути удален один черный узел, поэтому свойства RB сохранены. Высота черного дерева уменьшается на 1.

  // Case_D1 (P == NULL):
  return; // deletion complete

Удалить дело D2

→ Пояснения к символам

первая итерация

более высокая итерация

Удалить дело D2

Дети P , S и S — черные. После окраски S в красный цвет все пути, проходящие через S , а именно те пути, которые не проходят через N , имеют на один черный узел меньше. Теперь все пути в поддереве, корнем которого является P, имеют одинаковое количество черных узлов, но на один меньше, чем пути, не проходящие через P , поэтому требование 4 все равно может быть нарушено. После перемаркировки P на N выполняется инвариант цикла , так что ребалансировку можно повторить на один уровень черного (= 1 уровень дерева) выше.

    // Case_D2 (P+C+S+D black):
    S->color = RED;
    N = P; // new current node (maybe the root)
    // iterate 1 black level
    //   (= 1 tree level) higher
  } while ((P = N->parent) != NULL);
  // end of the (do while)-loop
  // (with return;)

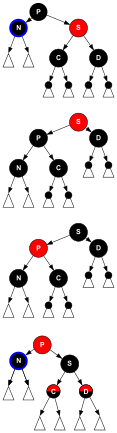
Удалить обращение D3

первая итерация

более высокая итерация

Удалить обращение D3

Брат S красный, поэтому P и племянники C и D должны быть черными. А dir-поворот в точке P превращает S в N. прародителя Затем, после того, как цвета P и S поменялись местами , путь через N все еще остается коротким на один черный узел. Но теперь у N есть красный родительский элемент P , а после переназначения — черный родственный элемент S , поэтому преобразования в случаях D4, D5 или D6 способны восстановить RB-форму.

Case_D3: // S red && P+C+D black:
  RotateDirRoot(T,P,dir); // P may be the root
  P->color = RED;
  S->color = BLACK;
  S = C; // != NIL
  // now: P red && S black
  D = S->child[1-dir]; // distant nephew
  if (D != NIL && D->color == RED)
    goto Case_D6;      // D red && S black
  C = S->child[  dir]; // close   nephew
  if (C != NIL && C->color == RED)
    goto Case_D5;      // C red && S+D black
  // Otherwise C+D considered black.
  // fall through to Case_D4

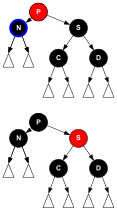
Удалить дело D4

первая итерация

более высокая итерация

Удалить дело D4

Дети брата и сестры S и S черные, а P — красный. Обмен цветов S и P не влияет на количество черных узлов на путях, проходящих через S , но добавляет один к количеству черных узлов на путях, проходящих через N , компенсируя удаленный черный узел на этих путях.

Case_D4: // P red && S+C+D black:
  S->color = RED;
  P->color = BLACK;
  return; // deletion complete

Удалить дело D5

первая итерация

более высокая итерация

Удалить дело D5

Родной брат S — черный, красный ближайший дочерний элемент S — , а D дальний дочерний элемент — черный. После (1-dir)-ротации в точке S племянник C становится новым родителем S и N. братом или сестрой Цвета S и C меняются местами. Все пути по-прежнему имеют одинаковое количество черных узлов, но теперь у N есть черный брат, далекий дочерний элемент которого красный, поэтому созвездие подходит для случая D6. Это преобразование не ни N , ни его родительского P затрагивает , и P может быть красным или черным ( на схеме).

Case_D5: // C red && S+D black:
  RotateDir(S,1-dir); // S is never the root
  S->color = RED;
  C->color = BLACK;
  D = S;
  S = C;
  // now: D red && S black
  // fall through to Case_D6

Удалить дело D6

первая итерация

более высокая итерация

Удалить дело D6

Родной брат S — черный, D дальний ребенок S — — красный. После dir-поворот в точке P, брат S становится родителем P и элемента удаленного дочернего D . Цвета P и S меняются местами, и D становится черным. Все поддерево по-прежнему имеет один и тот же цвет в корне S , а именно красный или черный ( на диаграмме), который относится к одному и тому же цвету как до, так и после преобразования. Таким образом, требование 3 сохраняется. Пути в поддереве, не проходящие через N (теперь проходящие через D и узел 3 на диаграмме), проходят через то же количество черных узлов, что и раньше, но у N теперь есть еще один черный предок: либо P стал черным, либо был черный и S были добавлены как черный дедушка. Таким образом, пути, проходящие через N, проходят через один дополнительный черный узел, так что требование 4 восстановлено и все дерево имеет RB-форму.

Case_D6: // D red && S black:
  RotateDirRoot(T,P,dir); // P may be the root
  S->color = P->color;
  P->color = BLACK;
  D->color = BLACK;
  return; // deletion complete
} // end of RBdelete2

Поскольку алгоритм преобразует входные данные без использования вспомогательной структуры данных и использует лишь небольшой объем дополнительного пространства для хранения вспомогательных переменных, он находится на месте .

Доказательство границ

Рис. 4. Красно-черные деревья RB _h высот h =1,2,3,4,5,
каждый с минимальным количеством 1,2,4,6 соотв. 10 узлов.

Для $h\in \mathbb {N}$ есть красно-черное дерево высоты $h$ с

$m_{h}$	$=2^{\lfloor (h+1)/2\rfloor }+2^{\lfloor h/2\rfloor }-2$
	$={\Biggl \{}$	$2\cdot 2^{\tfrac {h}{2}}-2=2^{{\tfrac {h}{2}}+1}-2$		если $h$ даже
	$3\cdot 2^{\tfrac {h-1}{2}}-2$		если $h$ странный

узлы ( $\lfloor \,\rfloor$ — функция пола ) и не существует красно-черного дерева такой высоты с меньшим количеством узлов — поэтому оно минимально .
Его черная высота $\lceil h/2\rceil$ (с черным корнем) или для нечетного $h$ (тогда с красным корнем) тоже $(h-1)/2~.$

Доказательство

Чтобы красно-черное дерево определенной высоты имело минимальное количество узлов, оно должно иметь ровно один самый длинный путь с максимальным количеством красных узлов, чтобы достичь максимальной высоты дерева с минимальной высотой черного цвета. Помимо этого пути, все остальные узлы должны быть черными. Если узел удаляется из этого дерева, он либо теряет высоту, либо какое-то свойство RB.

Дерево высот RB $h=1$ с красным корнем минимальна. Это согласно с

$m_{1}=2^{\lfloor (1+1)/2\rfloor }\!+\!2^{\lfloor 1/2\rfloor }\!\!-\!\!2=2^{1}\!+\!2^{0}\!\!-\!\!2=1~.$

Минимальное дерево RB (RB _h на рисунке 4) высоты $h>1$ имеет корень, два дочерних поддерева которого имеют разную высоту. Поддерево более высокого дочернего уровня также является минимальным деревом RB, RB _{h –1} , содержащим также самый длинный путь, определяющий его высоту. $h\!\!-\!\!1$; у него есть $m_{h-1}$ узлы и черная высота $\lfloor (h\!\!-\!\!1)/2\rfloor =:s.$ Другое поддерево — идеальное двоичное дерево (черной) высоты. $s$ имея $2^{s}\!\!-\!\!1=2^{\lfloor (h-1)/2\rfloor }\!\!-\!\!1$ черные узлы — и никакого красного узла. Тогда количество узлов по индукции

	$m_{h}$	$=$	$(m_{h-1})$	$+$	$(1)$	$+$	$(2^{\lfloor (h-1)/2\rfloor }-1)$
			(высшее поддерево)		(корень)		(второе поддерево)
в результате чего
	$m_{h}$	$=$	$(2^{\lfloor h/2\rfloor }+2^{\lfloor (h-1)/2\rfloor }-2)$	$+$	$2^{\lfloor (h-1)/2\rfloor }$
		$=$	$2^{\lfloor h/2\rfloor }+2^{\lfloor (h+1)/2\rfloor }-2$  ■

График ​ функции $m_{h}$ выпукло с и кусочно-линейно точками излома в точках $(h=2k\;|\;m_{2k}=2\cdot 2^{k}\!-\!2)$ где $k\in \mathbb {N} .$ Функция была сведена в таблицу как $m_{h}=$ A027383( ч –1) для $h\geq 1$ (последовательность A027383 в OEIS ).

Решение функции для $h$

Неравенство $9>8=2^{3}$ приводит к $3>2^{3/2}$, что как ни странно $h$ приводит к

$m_{h}=3\cdot 2^{(h-1)/2}-2={\bigl (}3\cdot 2^{-3/2}{\bigr )}\cdot 2^{(h+2)/2}-2>2\cdot 2^{h/2}-2$.

Итак, как в четном, так и в нечетном случае: $h$ находится в интервале

	$\log _{2}(n+1)$	$\leq h\leq$	$2\log _{2}(n+2)-2=2\log _{2}(n/2+1)$	${\bigl [}<2\log _{2}(n+1)\;{\bigr ]}$
	(идеальное двоичное дерево)		(минимальное красно-черное дерево)

с $n$ количество узлов.

Заключение

Красно-черное дерево с $n$ узлы (ключи) имеют высоту дерева $h\in O(\log n).$

Операции над наборами и массовые операции

определены несколько операций над множествами В дополнение к операциям вставки, удаления и поиска отдельных элементов, для красно-черных деревьев : объединение , пересечение и разность множеств . быстрые массовые Затем на основе этих функций набора можно реализовать операции по вставке или удалению. Эти операции над множествами основаны на двух вспомогательных операциях: Split и Join . Благодаря новым операциям реализация красно-черных деревьев может стать более эффективной и поддающейся параллелизации. Для достижения временной сложности эта реализация требует, чтобы корень мог быть либо красным, либо черным, и чтобы каждый узел хранил свою собственную высоту черного цвета .

• Join : функция Join находится на двух красно-черных деревьях t ₁ и t ₂ и ключе k , где t ₁ < k < t ₂ , т.е. все ключи в t ₁ меньше k , а все ключи в t ₂ больше благодарить ​ . Он возвращает дерево, содержащее все элементы в t ₁ , t _2, а также в виде k .

Если два дерева имеют одинаковую высоту черного цвета, Join просто создает новый узел с левым поддеревом t ₁ , корнем k и правым поддеревом t ₂ . Если и t ₁ , и t ₂ имеют черный корень, установите k красным. В противном случае k устанавливается черным.

Если высоты черного цвета неравны, предположим, что высота черного цвета t ₁ больше, чем высота t ₂ (другой случай симметричен). Соединение следует за правым позвоночником t ₁ до черного узла c , который сбалансирован с t ₂ . новый узел с левым дочерним элементом c , корнем k (красным) и правым дочерним элементом t ₂ На этом этапе для замены c создается . Новый узел может сделать недействительным красно-черный инвариант, поскольку подряд могут появляться не более трех красных узлов. Это можно исправить двойным вращением. Если проблема с двойным красным цветом распространяется на корень, корень становится черным, восстанавливая свойства. Стоимостью этой функции является разница высот черного между двумя входными деревьями.

• Разделение : чтобы разделить красно-черное дерево на два меньших дерева: меньшее, чем ключ x , и больше, чем ключ x , сначала нарисуйте путь от корня, вставив x в красно-черное дерево. После этой вставки все значения меньше x будут найдены слева от пути, а все значения больше x будут найдены справа. Применяя Join , все поддеревья с левой стороны объединяются снизу вверх с использованием ключей на пути в качестве промежуточных узлов снизу вверх, чтобы сформировать левое дерево, а правая часть становится симметричной.

Для некоторых приложений Split также возвращает логическое значение, указывающее, присутствует ли x в дереве. Стоимость Сплита ​ $O(\log n),$ порядок высоты дерева. Этот алгоритм на самом деле не имеет ничего общего с какими-либо особыми свойствами красно-черного дерева и может использоваться для любого дерева с операцией соединения , такого как дерево AVL .

Алгоритм соединения следующий:

function joinRightRB(TL, k, TR):
    if (TL.color=black) and (TL.blackHeight=TR.blackHeight):
        return Node(TL,⟨k,red⟩,TR)
    T'=Node(TL.left,⟨TL.key,TL.color⟩,joinRightRB(TL.right,k,TR))
    if (TL.color=black) and (T'.right.color=T'.right.right.color=red):
        T'.right.right.color=black;
        return rotateLeft(T')
    return T' /* T''[recte T'] */

function joinLeftRB(TL, k, TR):
  /* symmetric to joinRightRB */

function join(TL, k, TR):
    if TL.blackHeight>TR.blackHeight:
        T'=joinRightRB(TL,k,TR)
        if (T'.color=red) and (T'.right.color=red):
            T'.color=black
        return T'
    if TR.blackHeight>TL.blackHeight:
        /* symmetric */
    if (TL.color=black) and (TR.color=black):
        return Node(TL,⟨k,red⟩,TR)
    return Node(TL,⟨k,black⟩,TR)

Алгоритм разделения следующий:

function split(T, k):
    if (T = nil) return (nil, false, nil)
    if (k = T.key) return (T.left, true, T.right)
    if (k < T.key):
        (L',b,R') = split(T.left, k)
        return (L',b,join(R',T.key,T.right))
    (L',b,R') = split(T.right, k)
    return (join(T.left,T.key,L'),b,T.right)

Объединение двух красно-черных деревьев t ₁ и t _2, представляющих множества A и B , представляет собой красно-черное дерево t , которое представляет A ∪ B . Следующая рекурсивная функция вычисляет это объединение:

function union(t1, t2):
    if t1 = nil return t2
    if t2 = nil return t1
    (L1,b,R1)=split(t1,t2.key)
    proc1=start:
        TL=union(L1,t2.left)
    proc2=start:
        TR=union(R1,t2.right)
    wait all proc1,proc2
    return join(TL, t2.key, TR)

Здесь разделение предполагается, что возвращает два дерева: одно содержит ключи меньшего входного ключа, а другое — большие ключи. (Алгоритм неразрушающий , но существует также деструктивная версия.)

Алгоритм пересечения или различия аналогичен, но требует вспомогательной процедуры Join2 , такой же, как и Join , но без среднего ключа. Благодаря новым функциям объединения, пересечения или различия в красно-черное дерево можно вставлять или удалять один или несколько ключей. Поскольку Split вызывает метод Join , но не занимается критериями балансировки красно-черных деревьев напрямую, такую ​​реализацию обычно называют реализацией, основанной на объединении .

Сложность каждого объединения, пересечения и различия равна $O\left(m\log \left({n \over m}+1\right)\right)$ за два красно-черных дерева размером $m$ и $n(\geq m)$. Эта сложность оптимальна по количеству сравнений. Что еще более важно, поскольку рекурсивные вызовы объединения, пересечения или различия независимы друг от друга, они могут выполняться параллельно с параллельной глубиной. $O(\log m\log n)$. Когда $m=1$, реализация на основе соединения имеет тот же вычислительно- ориентированный ациклический граф (DAG), что и одноэлементная вставка и удаление, если корень большего дерева используется для разделения меньшего дерева.

Параллельные алгоритмы

Параллельные алгоритмы построения красно-черных деревьев из отсортированных списков элементов могут выполняться за постоянное время или за постоянное время. $O(\log \log n)$ время, в зависимости от модели компьютера, если количество доступных процессоров асимптотически пропорционально количеству $n$ предметов, где $n\to \infty$. Известны также параллельные алгоритмы быстрого поиска, вставки и удаления.

Алгоритмы объединения для красно-черных деревьев параллельны для массовых операций, включая объединение, пересечение, построение, фильтрацию, сокращение карты и т. д.

Параллельные массовые операции

Базовые операции, такие как вставка, удаление или обновление, можно распараллелить, определив операции, которые обрабатывают большие объемы нескольких элементов. Также можно обрабатывать большие объемы данных с помощью нескольких основных операций, например, объемные файлы могут содержать элементы для вставки, а также элементы для удаления из дерева.

Алгоритмы для массовых операций применимы не только к красно-черному дереву, но могут быть адаптированы и к другим структурам данных отсортированных последовательностей, таким как дерево 2–3 , дерево 2–3–4 и (a,b)-дерево. . Далее будут объяснены различные алгоритмы массовой вставки, но те же алгоритмы можно применять и для удаления и обновления. Массовая вставка — это операция, которая вставляет каждый элемент последовательности. $I$ в дерево $T$.

На основе объединения

Этот подход можно применить к любой структуре данных отсортированной последовательности, которая поддерживает эффективные операции соединения и разделения. Общая идея состоит в том, чтобы разделить $I$ и $T$ в нескольких частях и выполняйте вставки в эти части параллельно.

1. Сначала основная масса $I$ количество вставляемых элементов должно быть отсортировано.
2. После этого алгоритм разбивает $I$ в $k\in \mathbb {N} ^{+}$ части $\langle I_{1},\cdots ,I_{k}\rangle$ примерно равных размеров.
3. Дальше дерево $T$ необходимо разделить на $k$ части $\langle T_{1},\cdots ,T_{k}\rangle$ в некотором смысле, так что для каждого $j\in \mathbb {N} ^{+}|\,1\leq j<k$ выполняются следующие ограничения:
   1. ${\text{last}}(I_{j})<{\text{first}}(T_{j+1})$
   2. ${\text{last}}(T_{j})<{\text{first}}(I_{j+1})$
4. Теперь алгоритм вставляет каждый элемент $I_{j}$ в $T_{j}$ последовательно. Этот шаг необходимо выполнить для каждого $j$, что можно сделать до $k$ процессоры параллельно.
5. Наконец, полученные деревья будут объединены, чтобы сформировать окончательный результат всей операции.

Обратите внимание, что на шаге 3 ограничения на разделение $I$ убедиться, что на шаге 5 деревья можно снова соединить и полученную последовательность отсортировать.

• 
  исходное дерево
• 
  разделить I и T
• 
  вставить в разрез Т
• 
  соединение

Псевдокод демонстрирует простую реализацию алгоритма массовой вставки на основе объединения по принципу «разделяй и властвуй». Оба рекурсивных вызова могут выполняться параллельно. Используемая здесь операция соединения отличается от версии, описанной в этой статье, вместо нее соединение2 используется , в котором отсутствует второй параметр k.

bulkInsert(T, I, k):
    I.sort()
    bulklInsertRec(T, I, k)

bulkInsertRec(T, I, k):
    if k = 1:
        forall e in I: T.insert(e)
    else
        m := ⌊size(I) / 2⌋
        (T1, _, T2) := split(T, I[m])
        bulkInsertRec(T1, I[0 .. m], ⌈k / 2⌉)
            || bulkInsertRec(T2, I[m + 1 .. size(I) - 1], ⌊k / 2⌋)
        T ← join2(T1, T2)

Время выполнения

Сортировка $I$ в данном анализе не учитывается.

#уровни рекурсии	$\in O(\log k)$
Т(разделить) + Т(объединить)	$\in O(\log |T|)$
вставки на ветку	$\in O\left({\frac {|I|}{k}}\right)$
Т(вставить)	$\in O(\log |T|)$
T(bulkInsert) с $k$ = #процессоры	$\in O\left(\log k\log |T|+{\frac {|I|}{k}}\log |T|\right)$

Это можно улучшить, используя параллельные алгоритмы разделения и соединения. В этом случае время выполнения $\in O\left(\log |T|+{\frac {|I|}{k}}\log |T|\right)$.

Работа

#разделяет, #объединяет	$\in O(k)$
W(разделить) + W(объединить)	$\in O(\log |T|)$
#вставки	$\in O(|I|)$
Вт (вставить)	$\in O(\log |T|)$
W(объемная вставка)	$\in O(k\log |T|+|I|\log |T|)$

Конвейерная обработка

Другой метод распараллеливания массовых операций — использование конвейерного подхода. Это можно сделать, разбив задачу обработки базовой операции на последовательность подзадач. Для нескольких базовых операций подзадачи могут обрабатываться параллельно, назначая каждую подзадачу отдельному процессору.

1. Сначала основная масса $I$ количество вставляемых элементов должно быть отсортировано.
2. Для каждого элемента в $I$ алгоритм находит соответствующую позицию вставки в $T$. Это можно сделать параллельно для каждого элемента. $\in I$ с $T$ не будет мутировать в этом процессе. Сейчас $I$ необходимо разделить на подпоследовательности $S$ в соответствии с позицией вставки каждого элемента. Например $s_{n,{\mathit {left}}}$ является подпоследовательностью $I$ который содержит элементы, позиция вставки которых будет слева от узла $n$.
3. Средний элемент $m_{n,{\mathit {dir}}}$ каждой подпоследовательности $s_{n,{\mathit {dir}}}$ будет вставлен в $T$ как новый узел $n'$. Это можно делать параллельно для каждого $m_{n,{\mathit {dir}}}$ поскольку по определению позиция вставки каждого $m_{n,{\mathit {dir}}}$ является уникальным. Если $s_{n,{\mathit {dir}}}$ содержит элементы слева или справа от $m_{n,{\mathit {dir}}}$, они будут содержаться в новом наборе подпоследовательностей $S$ как $s_{n',{\mathit {left}}}$ или $s_{n',{\mathit {right}}}$.
4. Сейчас $T$ возможно, содержит до двух последовательных красных узлов в конце путей от корня к листьям, которые необходимо исправить. Обратите внимание, что при ремонте положение вставки элементов $\in S$ должны быть обновлены, если соответствующие узлы затронуты вращением.
   Если два узла имеют разных ближайших черных предков, их можно восстанавливать параллельно. Поскольку не более четырех узлов могут иметь одного и того же ближайшего черного предка, узлы на самом низком уровне можно восстановить за постоянное количество параллельных шагов.
   Этот шаг будет последовательно применяться к указанным выше уровням черного до тех пор, пока $T$ полностью отремонтирован.
5. Шаги с 3 по 5 будут повторяться в новых подпоследовательностях до тех пор, пока $S$ пусто. В этот момент каждый элемент $\in I$ был вставлен. Каждое применение этих шагов называется этапом . Поскольку длина подпоследовательностей в $S$ является $\in O(|I|)$ и на каждом этапе подпоследовательности сокращаются вдвое, количество этапов равно $\in O(\log |I|)$.
   Поскольку все этапы перемещаются вверх по черным уровням дерева, их можно распараллелить в конвейере. Как только этап завершает обработку одного уровня черного, следующий этап может перейти вверх и продолжить работу на этом уровне.

• 
  Начальное дерево
• 
  Найдите позиции вставки
• 
  Этап 1 вставляет элементы
• 
  1 этап начинается ремонт узлов
• 
  Этап 2 вставляет элементы
• 
  2 этап начинается ремонт узлов
• 
  Этап 3 вставляет элементы
• 
  3 этап начинается ремонт узлов
• 
  3 этап продолжает ремонт узлов

Время выполнения

Сортировка $I$ в данном анализе не учитывается. Также, $|I|$ предполагается меньшим, чем $|T|$, в противном случае эффективнее было бы построить полученное дерево с нуля.

T(найти позицию вставки)	$\in O(\log |T|)$
#этапы	$\in O(\log |I|)$
Т(вставка) + Т(ремонт)	$\in O(\log |T|)$
T(bulkInsert) с $|I|$ ~ #процессоры	$\in O(\log |I|+2\cdot \log |T|)$ $=O(\log |T|)$

Работа

W(найти позиции вставки)	$\in O(|I|\log |T|)$
#вставки, #ремонт	$\in O(|I|)$
W(вставка) + W(ремонт)	$\in O(\log |T|)$
W(объемная вставка)	$\in O(2\cdot |I|\log |T|)$ $=O(|I|\log |T|)$

См. также

• Список структур данных
• Древовидная структура данных
• Вращение дерева
• Дерево статистики заказа
• Дерево АА , разновидность красно-черного дерева.
• Наклоняющееся влево красно-черное дерево.
• АВЛ-дерево
• B-дерево ( дерево 2–3 , дерево 2–3–4 , B+ дерево , B*-дерево , UB-дерево )
• Дерево козла отпущения
• Распространение дерева
• Т-образное дерево
• WAVL-дерево

Дальнейшее чтение

• Mathworld: Красно-черное дерево
• Государственный университет Сан-Диего: CS 660: Красно-черные заметки о дереве , Роджер Уитни.
• Пфафф, Бен (июнь 2004 г.). «Анализ производительности BST в системном программном обеспечении» (PDF) . Стэнфордский университет .

Внешние ссылки

• Бен Пфафф: Введение в бинарные деревья поиска и сбалансированные деревья. Фонд свободного программного обеспечения, Бостон, 2004 г., ftp.gnu.org (PDF gzip; 1662 КБ)
• Полная и работающая реализация на C.
• MIT о красно-черных деревьях OCW Лекция Эрика Демейна
• Визуализация вставки двоичного дерева поиска на YouTube - Визуализация вставки случайных и предварительно отсортированных данных в элементарных двоичных деревьях поиска и красно-черных деревьях, наклоненных влево.
• Навязчивое красно-черное дерево, написанное на C++.
• Красно-черные BST в сбалансированных деревьях поиска 3.3
• Красно-черный BST Демо