Роза (топология)

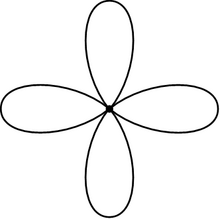
В математике роза полученное (также известная как букет из n кругов ) — это топологическое пространство, склеиванием набора кругов вдоль одной точки. Круги розы называются лепестками . Розы играют важную роль в алгебраической топологии , где они тесно связаны со свободными группами .

Определение

Роза представляет совокупность кругов . собой То есть роза — это фактор-пространство C / S , где C — непересекающееся объединение окружностей, а S — множество, состоящее из одной точки из каждой окружности. Как клеточный комплекс , роза имеет одну вершину и одно ребро для каждого круга. Это делает его простым примером топологического графа .

Розу с n лепестками также можно получить, определив n точек на одном круге. Роза с двумя лепестками известна как восьмерка .

Отношение к свободным группам

Основная группа розы бесплатна , с одним генератором для каждого лепестка. Универсальное покрытие представляет собой бесконечное дерево, которое можно отождествить с графом Кэли свободной группы. (Это частный случай комплекса представлений , связанный с любым представлением группы .)

Промежуточные покровы розы соответствуют подгруппам свободной группы. Наблюдение того, что любое покрытие розы является графом, дает простое доказательство того, что каждая подгруппа свободной группы свободна ( теорема Нильсена-Шрайера ).

Поскольку универсальное покрытие розы сжимаемо , роза на самом деле является пространством Эйленберга-Маклейна для ассоциированной свободной F. группы Отсюда следует, что когомологий группы H ^н( F ) тривиальны для n ≥ 2.

Другие объекты недвижимости

Любой связный граф розе гомотопически эквивалентен . В частности, роза — это фактор-пространство графа, полученного схлопыванием связующего дерева .
Диск деформируется с удаленными n точками (или сфера с удаленными n + 1 точками) , превращаясь в розу с n лепестками. Каждую из удаленных точек окружает один лепесток розы.
Тор . с удаленной деформацией в одной точке втягивается в восьмерку, а именно в объединение двух образующих окружностей В более общем смысле, поверхность рода g с удаленной в одной точке деформацией втягивается в розу с 2 лепестками g , а именно на границу фундаментального многоугольника .
У розы может быть бесконечное количество лепестков, что приводит к фундаментальной группе, которая свободна в бесконечном числе генераторов. Роза со счетным и бесконечным числом лепестков подобна гавайской серьге : существует непрерывная биекция от этой розы на гавайскую серьгу, но они не гомеоморфны . Роза с бесконечным количеством лепестков не компактна, а гавайская серьга компактна.

См. также

Ссылки

Хэтчер, Аллен (2002), Алгебраическая топология , Кембридж, Великобритания: Издательство Кембриджского университета, ISBN 0-521-79540-0
Манкрес, Джеймс Р. (2000), Топология , Энглвуд Клиффс, Нью-Джерси: Prentice Hall, Inc, ISBN 0-13-181629-2
Стиллвелл, Джон (1993), Классическая топология и комбинаторная теория групп , Берлин: Springer-Verlag, ISBN 0-387-97970-0