ПРИХОДИТЬ +
 | |
| Парадигма | Действие |
|---|---|
| Разработано | Лесли Лэмпорт |
| Впервые появился | 23 апреля 1999 г [1] |
| Стабильная версия | ПРИХОДИТЬ +2
/ 15 января 2014 г [2] |
| Язык реализации | Ява |
| ТЫ | Кроссплатформенность (мультиплатформенность) |
| Лицензия | МОЯ лицензия [3] |
| Расширения имен файлов | .воля |
| Веб-сайт | порт лампы |
ПРИХОДИТЬ + — язык формальных спецификаций, разработанный Лесли Лэмпортом . Он используется для проектирования, моделирования, документирования и проверки программ, особенно параллельных и распределенных систем . TLA + считается полностью тестируемым псевдокодом , [4] и его использование можно сравнить с рисованием чертежей программных систем; [5] TLA — это аббревиатура от Temporal Logic of Actions .
Для проектирования и документации TLA + выполняет ту же цель, что и неофициальные технические спецификации . Однако ТЛА + спецификации написаны на формальном языке логики и математики, и точность спецификаций, написанных на этом языке, предназначена для выявления недостатков проектирования до того, как начнется реализация системы. [6]
Поскольку ТЛА + спецификации написаны на формальном языке, они поддаются конечной проверке модели . Средство проверки модели находит все возможные варианты поведения системы вплоть до некоторого количества шагов выполнения и проверяет их на наличие нарушений желаемых свойств инвариантности, таких как безопасность и живучесть . TLA + спецификации используют базовую теорию множеств для определения безопасности (плохие вещи не произойдут) и временную логику для определения жизнеспособности (хорошие вещи рано или поздно случаются).
ПРИХОДИТЬ + также используется для написания проверяемых машиной доказательств правильности как алгоритмов , так и математических теорем. Доказательства написаны в декларативном иерархическом стиле, независимом от какого-либо отдельного механизма доказательства теорем. Как формальные, так и неформальные структурированные математические доказательства могут быть написаны в TLA. + ; язык похож на LaTeX , и существуют инструменты для перевода TLA. + спецификации к документам LaTeX. [7]
ПРИХОДИТЬ + был представлен в 1999 году после нескольких десятилетий исследований метода проверки параллельных систем. С тех пор был разработан набор инструментов, включающий IDE и средство проверки распределенных моделей. Псевдокодоподобный язык PlusCal был создан в 2009 году; он транспилируется в TLA + и полезен для определения последовательных алгоритмов. TLA +2 был анонсирован в 2014 году, расширяя языковую поддержку конструкций доказательства. Текущий TLA + ссылка - ПРИХОДЯЩЕЕ + Гиперкнига Лесли Лэмпорт.
История
[ редактировать ]
Современная темпоральная логика была разработана Артуром Прайором в 1957 году и тогда называлась временной логикой. Хотя Амир Пнуэли был первым, кто серьезно изучил применение темпоральной логики в информатике , Прайор размышлял о ее использовании десятилетием ранее, в 1967 году:
Полезность систем такого типа [в отношении дискретного времени] не зависит от какого-либо серьезного метафизического предположения о дискретности времени; они применимы в ограниченных областях дискурса, в которых нас интересует только то, что происходит дальше в последовательности дискретных состояний, например, при работе цифрового компьютера.
Пнуэли исследовал использование темпоральной логики при описании и рассуждениях о компьютерных программах, представив линейную темпоральную логику в 1977 году. LTL стал важным инструментом для анализа параллельных программ, легко выражая такие свойства, как взаимное исключение и свобода от тупиков . [8]
Одновременно с работой Пнуэли над LTL ученые работали над обобщением логики Хоара для проверки многопроцессных программ. Лесли Лэмпорт заинтересовался этой проблемой после того, как экспертная оценка обнаружила ошибку в представленной им статье о взаимном исключении. Эд Эшкрофт представил инвариантность в своей статье 1975 года «Доказательство утверждений о параллельных программах», которую Лэмпорт использовал для обобщения метода Флойда в своей статье 1977 года «Доказательство корректности многопроцессных программ». В статье Лэмпорта безопасность и жизнеспособность также представлены как обобщения частичной корректности и завершения соответственно. [9] Этот метод использовался для проверки первого алгоритма параллельной сборки мусора в статье 1978 года с Эдсгером Дейкстрой . [10]
Лэмпорт впервые столкнулся с LTL Пнуэли во время семинара в Стэнфорде в 1978 году, организованного Сьюзен Овики . По словам Лэмпорта, «я был уверен, что темпоральная логика — это какая-то абстрактная чепуха, которая никогда не будет иметь никакого практического применения, но это казалось забавным, поэтому я присутствовал». В 1980 году он опубликовал статью «Когда-нибудь — это иногда не никогда», которая стала одной из наиболее часто цитируемых статей в литературе по темпоральной логике. [11] Лэмпорт работал над написанием спецификаций темпоральной логики во время своего пребывания в SRI , но счел этот подход непрактичным:

Однако я разочаровался во временной логике, когда увидел, как Шварц, Меллиар-Смит и Фриц Фогт проводили дни, пытаясь определить простую очередь FIFO , споря о том, достаточны ли перечисленные ими свойства. Я понял, что, несмотря на эстетическую привлекательность, написание спецификации как совокупности временных свойств на практике не работает. [12]
Его поиск практического метода спецификации привел к появлению в 1983 году статьи «Определение модулей параллельного программирования», в которой была представлена идея описания переходов состояний как булевых функций штрихованных и нештрихованных переменных. [12] Работа продолжалась на протяжении 1980-х годов, и Лэмпорт начал публиковать статьи о временной логике действий в 1990 году; однако официально он не был представлен до тех пор, пока в 1994 году не была опубликована «Временная логика действий». TLA позволил использовать действия во временных формулах, что, по словам Лэмпорта, «обеспечивает элегантный способ формализовать и систематизировать все рассуждения, используемые в параллельных системах». проверка». [13]
Спецификации TLA в основном состояли из обычной нетемпоральной математики, которую Лэмпорт нашел менее громоздкой, чем чисто временная спецификация. TLA предоставил математическую основу для языка спецификаций TLA. + , представленный в статье «Определение параллельных систем с помощью TLA». + "в 1999 году. [1] Позже в том же году Юань Юй написал средство проверки модели TLC для TLA. + спецификации; TLC использовался для поиска ошибок в когерентности кэша протоколе мультипроцессора Compaq . [14]
Лэмпорт опубликовал полный учебник по TLA + в 2002 году под названием «Спецификация систем: TLA». + Язык и инструменты для инженеров-программистов». [15] PlusCal был представлен в 2009 году. [16] и ТЛА + система доказательств (TLAPS) в 2012 году. [17] ПРИХОДИТЬ +2 был анонсирован в 2014 году, в него были добавлены некоторые дополнительные языковые конструкции, а также значительно увеличена языковая поддержка системы доказательств. [2] Лэмпорт занимается созданием обновленного TLA + ссылка "ТЛА + Гиперкнига». Неполную работу можно найти на его официальном сайте. Лэмпорт также создает The TLA. + Видеокурс , описанный в нем как «незавершенная работа, состоящая из начала серии видеолекций, призванных научить программистов и разработчиков программного обеспечения тому, как писать свои собственные TLA». + характеристики».
Язык
[ редактировать ]ПРИХОДИТЬ + спецификации организованы в модули. Модули могут расширять (импортировать) другие модули, чтобы использовать их функциональность. Хотя ТЛА + стандарт указывается в наборе математических символов, существующих TLA + инструменты используют LaTeX -подобные определения символов в ASCII . TLA + использует несколько терминов, которые требуют определения:
- Состояние – присвоение значений переменным.
- Поведение – последовательность состояний
- Шаг – пара последовательных состояний поведения.
- Шаг заикания - шаг, на котором переменные не изменяются.
- Отношение следующего состояния - отношение, описывающее, как переменные могут изменяться на любом этапе.
- Функция состояния - выражение, содержащее переменные и константы, которое не является отношением следующего состояния.
- Предикат состояния - функция состояния с логическим значением.
- Инвариант - предикат состояния истинен во всех достижимых состояниях.
- Темпоральная формула - выражение, содержащее утверждения темпоральной логики.
Безопасность
[ редактировать ]ПРИХОДИТЬ + занимается определением набора всех правильных поведений системы. Например, однобитовые часы, бесконечно тикающие между 0 и 1, можно задать следующим образом:
VARIABLE clock
Init == clock \in {0, 1}
Tick == IF clock = 0 THEN clock' = 1 ELSE clock' = 0
Spec == Init /\ [][Tick]_<<clock>>
Отношение следующего состояния Tick устанавливает clock ′ (значение часов в следующем состоянии) равным 1, если тактовый сигнал равен 0, и 0, если тактовый сигнал равен 1. Предикат состояния Init истинен, если значение тактового сигнала равно 0 или 1. Спецификация — это временная формула, утверждающая, что все поведение однобитовых часов должно изначально удовлетворять требованиям Init и все шаги должны либо соответствовать тику , либо быть шагами с задержками. Два таких поведения:
0 -> 1 -> 0 -> 1 -> 0 -> ...
1 -> 0 -> 1 -> 0 -> 1 -> ...
Свойства безопасности однобитных часов – набора достижимых состояний системы – адекватно описаны в спецификации.
живость
[ редактировать ]Приведенная выше спецификация запрещает странные состояния однобитных часов, но не говорит, что часы когда-либо будут тикать. Например, допустимо следующее поведение, связанное с постоянным заиканием:
0 -> 0 -> 0 -> 0 -> 0 -> ...
1 -> 1 -> 1 -> 1 -> 1 -> ...
Часы, которые не тикают, бесполезны, поэтому такое поведение следует запретить. Одно из решений — отключить заикание, но TLA + требует, чтобы заикание всегда было включено; шаг заикания представляет собой изменение какой-то части системы, не описанной в спецификации, и полезен для доработки . Чтобы гарантировать, что часы в конечном итоге должны идти, слабая справедливость утверждается для Tick :
Spec == Init /\ [][Tick]_<<clock>> /\ WF_<<clock>>(Tick)
Слабая справедливость в отношении действия означает, что если это действие постоянно разрешено, в конечном итоге оно должно быть предпринято. При слабой справедливости на Тике между тиками допускается только конечное число заикающихся шагов. Это временное логическое утверждение о Тике называется утверждением живучести. В общем, утверждение жизнеспособности должно быть машинно-замкнутым : оно не должно ограничивать набор достижимых состояний, а только набор возможных поведений. [18]
Большинство спецификаций не требуют подтверждения свойств живучести. Свойства безопасности достаточны как для проверки модели, так и для руководства при внедрении системы. [19]
Операторы
[ редактировать ]ПРИХОДИТЬ + основан на ZF , поэтому операции с переменными включают манипуляции с множествами. Язык включает в себя операторы членства в множестве , объединения , пересечения , разности , степенного набора и подмножества . Также включены логические операторы первого порядка, такие как ∨ , ∧ , ¬ , ⇒ , ↔ , ≡ , а также универсальные и экзистенциальные кванторы ∀ и ∃ . Гильберта ε предоставляется как оператор CHOOSE, который однозначно выбирает произвольный элемент множества. Арифметические операторы над действительными , целыми и натуральными числами доступны в стандартных модулях.
Операторы темпоральной логики встроены в TLA. + . Использование временных формул означает, что P всегда истинно, и означает, что P в конечном итоге истинно. Операторы объединены в означать, что P истинно бесконечно часто, или означает, что в конечном итоге P всегда будет правдой. Другие временные операторы включают слабую и сильную справедливость. Слабая справедливость WF e ( A ) означает, что если действие A разрешено постоянно (т. е. без перерывов), в конечном итоге оно должно быть выполнено. Сильная справедливость SF e ( A ) означает, что если действие A разрешено постоянно (многократно, с перерывами или без них), в конечном итоге оно должно быть выполнено.
Временная экзистенциальная и универсальная количественная оценка включены в TLA. + , хотя и без поддержки со стороны инструментов.
Пользовательские операторы аналогичны макросам . Операторы отличаются от функций тем, что их домен не обязательно должен быть множеством: например, оператор членства в множестве имеет в качестве своего домена категорию множеств , которая не является допустимым набором в ZFC (поскольку ее существование приводит к парадоксу Рассела ). В TLA добавлены рекурсивные и анонимные пользовательские операторы. +2 .
Структуры данных
[ редактировать ]Основная структура данных TLA + это набор. Множества либо перечисляются явно, либо создаются из других наборов с помощью операторов или с помощью {x \in S : p} где p — некоторое условие на x , или {e : x \in S} где e — некоторая функция от x . Уникальное пустое множество представляется как {}.
Функции в TLA + присвойте значение каждому элементу в своем домене, наборе. [S -> T] это набор всех функций с f[ x ] в T для каждого x в доменов наборе S. — Например, ТЛА + функция Double[x \in Nat] == x*2 является элементом множества [Nat -> Nat] так Double \in [Nat -> Nat] это верное утверждение в TLA + . Функции также определяются с помощью [x \in S |-> e] для некоторого выражения e или изменив существующую функцию [f EXCEPT ![v1] = v2].
Записи — это тип функции в TLA. + . Рекорд [name |-> "John", age |-> 35] это запись с именем полей и возрастом, доступ к которой осуществляется с помощью r.name и r.age, и принадлежащий множеству записей [name : String, age : Nat].
Кортежи включены в TLA + . Они явно определены с помощью <<e1,e2,e3>> или создан с помощью операторов из стандартного модуля «Последовательности». Наборы кортежей определяются декартовым произведением ; например, определяется множество всех пар натуральных чисел Nat \X Nat.
Стандартные модули
[ редактировать ]ПРИХОДИТЬ + имеет набор стандартных модулей, содержащих общие операторы. Они распространяются с помощью синтаксического анализатора. Средство проверки модели TLC использует реализации Java для повышения производительности.
- FiniteSets : Модуль для работы с конечными множествами . Предоставляет IsFiniteSet(S) и Cardinality(S) . операторы
- Последовательности : определяют операторы для кортежей, такие как Len(S) , Head(S) , Tail(S) , Append(S, E) , конкатенация и фильтр .
- Сумки : Модуль для работы с мультисетами . Предоставляет аналоги операций с примитивными наборами и подсчет дубликатов.
- Naturals : определяет натуральные числа вместе с неравенствами и арифметическими операторами.
- Целые числа : определяет целые числа .
- Reals : определяет действительные числа, а также деление и бесконечность .
- RealTime : предоставляет определения, полезные для системных спецификаций реального времени .
- TLC : предоставляет служебные функции для спецификаций, проверяемых моделью, таких как ведение журнала и утверждения.
Стандартные модули импортируются с помощью EXTENDS или INSTANCE заявления.
Инструменты
[ редактировать ]ИДЕТ
[ редактировать ] ПРИХОДИТЬ + IDE при типичном использовании показывает обозреватель спецификаций слева, редактор посередине и ошибки синтаксического анализа справа. | |
| Оригинальный автор(ы) | Саймон Замбровски, Маркус Куппе, Дэниэл Рикеттс |
|---|---|
| Разработчик(и) | Хьюлетт-Паккард , Microsoft |
| Первоначальный выпуск | 4 февраля 2010 г |
| Стабильная версия | 1.7.2 Теано
/ 2 февраля 2022 г |
| Предварительный выпуск | 1.8.0 Кларк
/ 6 декабря 2020 г |
| Репозиторий | github |
| Написано в | Ява |
| Доступно в | Английский |
| Тип | Интегрированная среда разработки |
| Лицензия | МОЯ лицензия |
| Веб-сайт | исследовать |
Интегрированная среда разработки реализована поверх Eclipse . Он включает в себя редактор с подсветкой ошибок и синтаксиса , а также интерфейс с графическим интерфейсом для нескольких других TLA. + инструменты:
- Синтаксический анализатор SANY, который анализирует и проверяет спецификацию на наличие синтаксических ошибок.
- Переводчик LaTeX для создания красиво напечатанных спецификаций.
- Переводчик PlusCal.
- Средство проверки модели TLC.
- Система доказательств TLAPS.
IDE распространяется в составе The TLA Toolbox .
Проверка модели
[ редактировать ]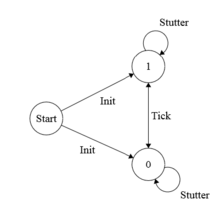
TLC Средство проверки модели строит конечным состоянием . модель TLA с + спецификации для проверки свойств инвариантности . TLC генерирует набор начальных состояний, удовлетворяющих спецификации, затем выполняет поиск в ширину по всем определенным переходам состояний. Выполнение прекращается, когда все переходы между состояниями приводят к уже обнаруженным состояниям. Если TLC обнаруживает состояние, которое нарушает системный инвариант, он останавливается и предоставляет путь трассировки состояния к состоянию-нарушителю. TLC предоставляет метод объявления симметрии модели для защиты от комбинаторного взрыва . [14] Он также распараллеливает этап исследования состояния и может работать в распределенном режиме, чтобы распределить рабочую нагрузку между большим количеством компьютеров. [20]
В качестве альтернативы исчерпывающему поиску в ширину TLC может использовать поиск в глубину или генерировать случайное поведение. TLC работает на подмножестве TLA. + ; модель должна быть конечной и перечислимой, а некоторые временные операторы не поддерживаются. В распределенном режиме TLC не может проверять свойства жизнеспособности, а также проверять случайное или глубинное поведение. TLC доступен в виде инструмента командной строки или в комплекте с набором инструментов TLA.
Система доказательств
[ редактировать ]ТЛА + Система доказательств, или TLAPS, механически проверяет доказательства, написанные на TLA. + . Он был разработан в Объединенном центре Microsoft Research - INRIA для доказательства корректности параллельных и распределенных алгоритмов. Язык доказательства спроектирован таким образом, чтобы быть независимым от какого-либо конкретного средства доказательства теорем; Доказательства пишутся в декларативном стиле и преобразуются в отдельные обязательства, которые отправляются проверяющим. Основными серверными пруверами являются Isabelle и Zenon, а в качестве альтернативы можно использовать SMT решатели CVC3 , Yices и Z3 . Доказательства TLAPS имеют иерархическую структуру, что упрощает рефакторинг и обеспечивает нелинейную разработку: работу можно начать на более поздних этапах до того, как будут проверены все предыдущие шаги, а сложные шаги разбиваются на более мелкие подэтапы. TLAPS хорошо работает с TLC, поскольку средство проверки модели быстро находит небольшие ошибки еще до начала проверки. В свою очередь, TLAPS может доказать свойства системы, которые выходят за рамки возможностей проверки конечной модели. [17]
TLAPS в настоящее время не поддерживает рассуждения с действительными числами и большинством темпоральных операторов. Изабель и Зенон, как правило, не могут доказать обязательства по арифметическому доказательству, требуя использования решателей SMT. [21] TLAPS использовался для доказательства правильности Byzantine Paxos , архитектуры безопасности Memoir, компонентов распределенной хеш-таблицы Pastry , [17] и алгоритм консенсуса Spire. [22] Он распространяется отдельно от остальной части TLA. + инструменты и является свободным программным обеспечением, распространяемым по лицензии BSD . [23] ПРИХОДИТЬ +2 значительно расширена языковая поддержка конструкций доказательства.
Промышленное использование
[ редактировать ]В Microsoft обнаружили критическую ошибку в модуле памяти Xbox 360 в процессе написания спецификации на TLA + . [24] ПРИХОДИТЬ + использовался для написания формальных доказательств корректности византийского Paxos и компонентов распределенной хеш-таблицы Pastry . [17]
Amazon Web Services использовала TLA + с 2011 года. ПРИХОДИТЕ + проверка модели на обнаруженные ошибки в DynamoDB , S3 , EBS и внутреннем менеджере распределенных блокировок; некоторые ошибки требовали трассировки состояния из 35 шагов. Проверка модели также использовалась для проверки агрессивной оптимизации. Кроме того, ТЛА + Было обнаружено, что спецификации имеют ценность в качестве документации и средств проектирования. [4] [25]
Microsoft Azure использовала TLA + разработать Cosmos DB , глобально распределенную базу данных с пятью различными моделями согласованности . [26] [27]
Altreonic NV использовал TLA + для модели проверьте OpenComRTOS .
Примеры
[ редактировать ]Хранилище ключей и значений с изоляцией снимков :
--------------------------- MODULE KeyValueStore ---------------------------
CONSTANTS Key, \* The set of all keys.
Val, \* The set of all values.
TxId \* The set of all transaction IDs.
VARIABLES store, \* A data store mapping keys to values.
tx, \* The set of open snapshot transactions.
snapshotStore, \* Snapshots of the store for each transaction.
written, \* A log of writes performed within each transaction.
missed \* The set of writes invisible to each transaction.
----------------------------------------------------------------------------
NoVal == \* Choose something to represent the absence of a value.
CHOOSE v : v \notin Val
Store == \* The set of all key-value stores.
[Key -> Val \cup {NoVal}]
Init == \* The initial predicate.
/\ store = [k \in Key |-> NoVal] \* All store values are initially NoVal.
/\ tx = {} \* The set of open transactions is initially empty.
/\ snapshotStore = \* All snapshotStore values are initially NoVal.
[t \in TxId |-> [k \in Key |-> NoVal]]
/\ written = [t \in TxId |-> {}] \* All write logs are initially empty.
/\ missed = [t \in TxId |-> {}] \* All missed writes are initially empty.
TypeInvariant == \* The type invariant.
/\ store \in Store
/\ tx \subseteq TxId
/\ snapshotStore \in [TxId -> Store]
/\ written \in [TxId -> SUBSET Key]
/\ missed \in [TxId -> SUBSET Key]
TxLifecycle ==
/\ \A t \in tx : \* If store != snapshot & we haven't written it, we must have missed a write.
\A k \in Key : (store[k] /= snapshotStore[t][k] /\ k \notin written[t]) => k \in missed[t]
/\ \A t \in TxId \ tx : \* Checks transactions are cleaned up after disposal.
/\ \A k \in Key : snapshotStore[t][k] = NoVal
/\ written[t] = {}
/\ missed[t] = {}
OpenTx(t) == \* Open a new transaction.
/\ t \notin tx
/\ tx' = tx \cup {t}
/\ snapshotStore' = [snapshotStore EXCEPT ![t] = store]
/\ UNCHANGED <<written, missed, store>>
Add(t, k, v) == \* Using transaction t, add value v to the store under key k.
/\ t \in tx
/\ snapshotStore[t][k] = NoVal
/\ snapshotStore' = [snapshotStore EXCEPT ![t][k] = v]
/\ written' = [written EXCEPT ![t] = @ \cup {k}]
/\ UNCHANGED <<tx, missed, store>>
Update(t, k, v) == \* Using transaction t, update the value associated with key k to v.
/\ t \in tx
/\ snapshotStore[t][k] \notin {NoVal, v}
/\ snapshotStore' = [snapshotStore EXCEPT ![t][k] = v]
/\ written' = [written EXCEPT ![t] = @ \cup {k}]
/\ UNCHANGED <<tx, missed, store>>
Remove(t, k) == \* Using transaction t, remove key k from the store.
/\ t \in tx
/\ snapshotStore[t][k] /= NoVal
/\ snapshotStore' = [snapshotStore EXCEPT ![t][k] = NoVal]
/\ written' = [written EXCEPT ![t] = @ \cup {k}]
/\ UNCHANGED <<tx, missed, store>>
RollbackTx(t) == \* Close the transaction without merging writes into store.
/\ t \in tx
/\ tx' = tx \ {t}
/\ snapshotStore' = [snapshotStore EXCEPT ![t] = [k \in Key |-> NoVal]]
/\ written' = [written EXCEPT ![t] = {}]
/\ missed' = [missed EXCEPT ![t] = {}]
/\ UNCHANGED store
CloseTx(t) == \* Close transaction t, merging writes into store.
/\ t \in tx
/\ missed[t] \cap written[t] = {} \* Detection of write-write conflicts.
/\ store' = \* Merge snapshotStore writes into store.
[k \in Key |-> IF k \in written[t] THEN snapshotStore[t][k] ELSE store[k]]
/\ tx' = tx \ {t}
/\ missed' = \* Update the missed writes for other open transactions.
[otherTx \in TxId |-> IF otherTx \in tx' THEN missed[otherTx] \cup written[t] ELSE {}]
/\ snapshotStore' = [snapshotStore EXCEPT ![t] = [k \in Key |-> NoVal]]
/\ written' = [written EXCEPT ![t] = {}]
Next == \* The next-state relation.
\/ \E t \in TxId : OpenTx(t)
\/ \E t \in tx : \E k \in Key : \E v \in Val : Add(t, k, v)
\/ \E t \in tx : \E k \in Key : \E v \in Val : Update(t, k, v)
\/ \E t \in tx : \E k \in Key : Remove(t, k)
\/ \E t \in tx : RollbackTx(t)
\/ \E t \in tx : CloseTx(t)
Spec == \* Initialize state with Init and transition with Next.
Init /\ [][Next]_<<store, tx, snapshotStore, written, missed>>
----------------------------------------------------------------------------
THEOREM Spec => [](TypeInvariant /\ TxLifecycle)
=============================================================================
на основе правил Брандмауэр :
------------------------------ MODULE Firewall ------------------------------
EXTENDS Integers
CONSTANTS Address, \* The set of all addresses
Port, \* The set of all ports
Protocol \* The set of all protocols
AddressRange == \* The set of all address ranges
{r \in Address \X Address : r[1] <= r[2]}
InAddressRange[r \in AddressRange, a \in Address] ==
/\ r[1] <= a
/\ a <= r[2]
PortRange == \* The set of all port ranges
{r \in Port \X Port : r[1] <= r[2]}
InPortRange[r \in PortRange, p \in Port] ==
/\ r[1] <= p
/\ p <= r[2]
Packet == \* The set of all packets
[sourceAddress : Address,
sourcePort : Port,
destAddress : Address,
destPort : Port,
protocol : Protocol]
Firewall == \* The set of all firewalls
[Packet -> BOOLEAN]
Rule == \* The set of all firewall rules
[remoteAddress : AddressRange,
remotePort : PortRange,
localAddress : AddressRange,
localPort : PortRange,
protocol : SUBSET Protocol,
allow : BOOLEAN]
Ruleset == \* The set of all firewall rulesets
SUBSET Rule
Allowed[rset \in Ruleset, p \in Packet] == \* Whether the ruleset allows the packet
LET matches == {rule \in rset :
/\ InAddressRange[rule.remoteAddress, p.sourceAddress]
/\ InPortRange[rule.remotePort, p.sourcePort]
/\ InAddressRange[rule.localAddress, p.destAddress]
/\ InPortRange[rule.localPort, p.destPort]
/\ p.protocol \in rule.protocol}
IN /\ matches /= {}
/\ \A rule \in matches : rule.allow
=============================================================================
Многовагонная лифтовая система:
------------------------------ MODULE Elevator ------------------------------
(***************************************************************************)
(* This spec describes a simple multi-car elevator system. The actions in *)
(* this spec are unsurprising and common to all such systems except for *)
(* DispatchElevator, which contains the logic to determine which elevator *)
(* ought to service which call. The algorithm used is very simple and does *)
(* not optimize for global throughput or average wait time. The *)
(* TemporalInvariant definition ensures this specification provides *)
(* capabilities expected of any elevator system, such as people eventually *)
(* reaching their destination floor. *)
(***************************************************************************)
EXTENDS Integers
CONSTANTS Person, \* The set of all people using the elevator system
Elevator, \* The set of all elevators
FloorCount \* The number of floors serviced by the elevator system
VARIABLES PersonState, \* The state of each person
ActiveElevatorCalls, \* The set of all active elevator calls
ElevatorState \* The state of each elevator
Vars == \* Tuple of all specification variables
<<PersonState, ActiveElevatorCalls, ElevatorState>>
Floor == \* The set of all floors
1 .. FloorCount
Direction == \* Directions available to this elevator system
{"Up", "Down"}
ElevatorCall == \* The set of all elevator calls
[floor : Floor, direction : Direction]
ElevatorDirectionState == \* Elevator movement state; it is either moving in a direction or stationary
Direction \cup {"Stationary"}
GetDistance[f1, f2 \in Floor] == \* The distance between two floors
IF f1 > f2 THEN f1 - f2 ELSE f2 - f1
GetDirection[current, destination \in Floor] == \* Direction of travel required to move between current and destination floors
IF destination > current THEN "Up" ELSE "Down"
CanServiceCall[e \in Elevator, c \in ElevatorCall] == \* Whether elevator is in position to immediately service call
LET eState == ElevatorState[e] IN
/\ c.floor = eState.floor
/\ c.direction = eState.direction
PeopleWaiting[f \in Floor, d \in Direction] == \* The set of all people waiting on an elevator call
{p \in Person :
/\ PersonState[p].location = f
/\ PersonState[p].waiting
/\ GetDirection[PersonState[p].location, PersonState[p].destination] = d}
TypeInvariant == \* Statements about the variables which we expect to hold in every system state
/\ PersonState \in [Person -> [location : Floor \cup Elevator, destination : Floor, waiting : BOOLEAN]]
/\ ActiveElevatorCalls \subseteq ElevatorCall
/\ ElevatorState \in [Elevator -> [floor : Floor, direction : ElevatorDirectionState, doorsOpen : BOOLEAN, buttonsPressed : SUBSET Floor]]
SafetyInvariant == \* Some more comprehensive checks beyond the type invariant
/\ \A e \in Elevator : \* An elevator has a floor button pressed only if a person in that elevator is going to that floor
/\ \A f \in ElevatorState[e].buttonsPressed :
/\ \E p \in Person :
/\ PersonState[p].location = e
/\ PersonState[p].destination = f
/\ \A p \in Person : \* A person is in an elevator only if the elevator is moving toward their destination floor
/\ \A e \in Elevator :
/\ (PersonState[p].location = e /\ ElevatorState[e].floor /= PersonState[p].destination) =>
/\ ElevatorState[e].direction = GetDirection[ElevatorState[e].floor, PersonState[p].destination]
/\ \A c \in ActiveElevatorCalls : PeopleWaiting[c.floor, c.direction] /= {} \* No ghost calls
TemporalInvariant == \* Expectations about elevator system capabilities
/\ \A c \in ElevatorCall : \* Every call is eventually serviced by an elevator
/\ c \in ActiveElevatorCalls ~> \E e \in Elevator : CanServiceCall[e, c]
/\ \A p \in Person : \* If a person waits for their elevator, they'll eventually arrive at their floor
/\ PersonState[p].waiting ~> PersonState[p].location = PersonState[p].destination
PickNewDestination(p) == \* Person decides they need to go to a different floor
LET pState == PersonState[p] IN
/\ ~pState.waiting
/\ pState.location \in Floor
/\ \E f \in Floor :
/\ f /= pState.location
/\ PersonState' = [PersonState EXCEPT ![p] = [@ EXCEPT !.destination = f]]
/\ UNCHANGED <<ActiveElevatorCalls, ElevatorState>>
CallElevator(p) == \* Person calls the elevator to go in a certain direction from their floor
LET pState == PersonState[p] IN
LET call == [floor |-> pState.location, direction |-> GetDirection[pState.location, pState.destination]] IN
/\ ~pState.waiting
/\ pState.location /= pState.destination
/\ ActiveElevatorCalls' =
IF \E e \in Elevator :
/\ CanServiceCall[e, call]
/\ ElevatorState[e].doorsOpen
THEN ActiveElevatorCalls
ELSE ActiveElevatorCalls \cup {call}
/\ PersonState' = [PersonState EXCEPT ![p] = [@ EXCEPT !.waiting = TRUE]]
/\ UNCHANGED <<ElevatorState>>
OpenElevatorDoors(e) == \* Open the elevator doors if there is a call on this floor or the button for this floor was pressed.
LET eState == ElevatorState[e] IN
/\ ~eState.doorsOpen
/\ \/ \E call \in ActiveElevatorCalls : CanServiceCall[e, call]
\/ eState.floor \in eState.buttonsPressed
/\ ElevatorState' = [ElevatorState EXCEPT ![e] = [@ EXCEPT !.doorsOpen = TRUE, !.buttonsPressed = @ \ {eState.floor}]]
/\ ActiveElevatorCalls' = ActiveElevatorCalls \ {[floor |-> eState.floor, direction |-> eState.direction]}
/\ UNCHANGED <<PersonState>>
EnterElevator(e) == \* All people on this floor who are waiting for the elevator and travelling the same direction enter the elevator.
LET eState == ElevatorState[e] IN
LET gettingOn == PeopleWaiting[eState.floor, eState.direction] IN
LET destinations == {PersonState[p].destination : p \in gettingOn} IN
/\ eState.doorsOpen
/\ eState.direction /= "Stationary"
/\ gettingOn /= {}
/\ PersonState' = [p \in Person |->
IF p \in gettingOn
THEN [PersonState[p] EXCEPT !.location = e]
ELSE PersonState[p]]
/\ ElevatorState' = [ElevatorState EXCEPT ![e] = [@ EXCEPT !.buttonsPressed = @ \cup destinations]]
/\ UNCHANGED <<ActiveElevatorCalls>>
ExitElevator(e) == \* All people whose destination is this floor exit the elevator.
LET eState == ElevatorState[e] IN
LET gettingOff == {p \in Person : PersonState[p].location = e /\ PersonState[p].destination = eState.floor} IN
/\ eState.doorsOpen
/\ gettingOff /= {}
/\ PersonState' = [p \in Person |->
IF p \in gettingOff
THEN [PersonState[p] EXCEPT !.location = eState.floor, !.waiting = FALSE]
ELSE PersonState[p]]
/\ UNCHANGED <<ActiveElevatorCalls, ElevatorState>>
CloseElevatorDoors(e) == \* Close the elevator doors once all people have entered and exited the elevator on this floor.
LET eState == ElevatorState[e] IN
/\ ~ENABLED EnterElevator(e)
/\ ~ENABLED ExitElevator(e)
/\ eState.doorsOpen
/\ ElevatorState' = [ElevatorState EXCEPT ![e] = [@ EXCEPT !.doorsOpen = FALSE]]
/\ UNCHANGED <<PersonState, ActiveElevatorCalls>>
MoveElevator(e) == \* Move the elevator to the next floor unless we have to open the doors here.
LET eState == ElevatorState[e] IN
LET nextFloor == IF eState.direction = "Up" THEN eState.floor + 1 ELSE eState.floor - 1 IN
/\ eState.direction /= "Stationary"
/\ ~eState.doorsOpen
/\ eState.floor \notin eState.buttonsPressed
/\ \A call \in ActiveElevatorCalls : \* Can move only if other elevator servicing call
/\ CanServiceCall[e, call] =>
/\ \E e2 \in Elevator :
/\ e /= e2
/\ CanServiceCall[e2, call]
/\ nextFloor \in Floor
/\ ElevatorState' = [ElevatorState EXCEPT ![e] = [@ EXCEPT !.floor = nextFloor]]
/\ UNCHANGED <<PersonState, ActiveElevatorCalls>>
StopElevator(e) == \* Stops the elevator if it's moved as far as it can in one direction
LET eState == ElevatorState[e] IN
LET nextFloor == IF eState.direction = "Up" THEN eState.floor + 1 ELSE eState.floor - 1 IN
/\ ~ENABLED OpenElevatorDoors(e)
/\ ~eState.doorsOpen
/\ nextFloor \notin Floor
/\ ElevatorState' = [ElevatorState EXCEPT ![e] = [@ EXCEPT !.direction = "Stationary"]]
/\ UNCHANGED <<PersonState, ActiveElevatorCalls>>
(***************************************************************************)
(* This action chooses an elevator to service the call. The simple *)
(* algorithm picks the closest elevator which is either stationary or *)
(* already moving toward the call floor in the same direction as the call. *)
(* The system keeps no record of assigning an elevator to service a call. *)
(* It is possible no elevator is able to service a call, but we are *)
(* guaranteed an elevator will eventually become available. *)
(***************************************************************************)
DispatchElevator(c) ==
LET stationary == {e \in Elevator : ElevatorState[e].direction = "Stationary"} IN
LET approaching == {e \in Elevator :
/\ ElevatorState[e].direction = c.direction
/\ \/ ElevatorState[e].floor = c.floor
\/ GetDirection[ElevatorState[e].floor, c.floor] = c.direction } IN
/\ c \in ActiveElevatorCalls
/\ stationary \cup approaching /= {}
/\ ElevatorState' =
LET closest == CHOOSE e \in stationary \cup approaching :
/\ \A e2 \in stationary \cup approaching :
/\ GetDistance[ElevatorState[e].floor, c.floor] <= GetDistance[ElevatorState[e2].floor, c.floor] IN
IF closest \in stationary
THEN [ElevatorState EXCEPT ![closest] = [@ EXCEPT !.floor = c.floor, !.direction = c.direction]]
ELSE ElevatorState
/\ UNCHANGED <<PersonState, ActiveElevatorCalls>>
Init == \* Initializes people and elevators to arbitrary floors
/\ PersonState \in [Person -> [location : Floor, destination : Floor, waiting : {FALSE}]]
/\ ActiveElevatorCalls = {}
/\ ElevatorState \in [Elevator -> [floor : Floor, direction : {"Stationary"}, doorsOpen : {FALSE}, buttonsPressed : {{}}]]
Next == \* The next-state relation
\/ \E p \in Person : PickNewDestination(p)
\/ \E p \in Person : CallElevator(p)
\/ \E e \in Elevator : OpenElevatorDoors(e)
\/ \E e \in Elevator : EnterElevator(e)
\/ \E e \in Elevator : ExitElevator(e)
\/ \E e \in Elevator : CloseElevatorDoors(e)
\/ \E e \in Elevator : MoveElevator(e)
\/ \E e \in Elevator : StopElevator(e)
\/ \E c \in ElevatorCall : DispatchElevator(c)
TemporalAssumptions == \* Assumptions about how elevators and people will behave
/\ \A p \in Person : WF_Vars(CallElevator(p))
/\ \A e \in Elevator : WF_Vars(OpenElevatorDoors(e))
/\ \A e \in Elevator : WF_Vars(EnterElevator(e))
/\ \A e \in Elevator : WF_Vars(ExitElevator(e))
/\ \A e \in Elevator : SF_Vars(CloseElevatorDoors(e))
/\ \A e \in Elevator : SF_Vars(MoveElevator(e))
/\ \A e \in Elevator : WF_Vars(StopElevator(e))
/\ \A c \in ElevatorCall : SF_Vars(DispatchElevator(c))
Spec == \* Initialize state with Init and transition with Next, subject to TemporalAssumptions
/\ Init
/\ [][Next]_Vars
/\ TemporalAssumptions
THEOREM Spec => [](TypeInvariant /\ SafetyInvariant /\ TemporalInvariant)
=============================================================================
См. также
[ редактировать ]- Коммуникация последовательных процессов
- Сплав (язык спецификации)
- B-метод
- Логика дерева вычислений
- ПлюсКал
- Временная логика
- Временная логика действий
- Z-обозначение
Ссылки
[ редактировать ]- ^ Jump up to: а б Лэмпорт, Лесли (январь 2000 г.). Определение параллельных систем с помощью TLA + (PDF) . Серия наук НАТО, III: Компьютерные и системные науки. Том. 173. Амстердам: IOS Press. стр. 183–247. ISBN 978-90-5199-459-9 . Проверено 22 мая 2015 г.
- ^ Jump up to: а б Лэмпорт, Лесли (15 января 2014 г.). "ТЛА +2 : Предварительное руководство» (PDF) . Проверено 2 мая 2015 г. .
- ^ «Инструменты Tlaplus — Лицензия» . КодПлекс . Майкрософт , Компак . 8 апреля 2013 года . Проверено 10 мая 2015 г. [ постоянная мертвая ссылка ] https://tlaplus.codeplex.com/license [ постоянная мертвая ссылка ]
- ^ Jump up to: а б Ньюкомб, Крис; Рат, Тим; Чжан, Фань; Мунтяну, Богдан; Брукер, Марк; Дирдауфф, Майкл (29 сентября 2014 г.). «Использование формальных методов в веб-сервисах Amazon» (PDF) . Амазонка . Проверено 8 мая 2015 г.
- ^ Лэмпорт, Лесли (25 января 2013 г.). «Почему мы должны создавать программное обеспечение так же, как мы строим дома» . Проводной . Проверено 7 мая 2015 г.
- ^
Лэмпорт, Лесли (18 июня 2002 г.). «7.1 Зачем указывать» . Спецификация систем: TLA + Язык и инструменты для инженеров аппаратного и программного обеспечения . Аддисон-Уэсли . п. 75. ИСБН 978-0-321-14306-8 .
Необходимость точного описания дизайна часто выявляет проблемы — тонкие взаимодействия и «крайние случаи», которые легко упустить из виду.
- ^ Лэмпорт, Лесли (2012). «Как написать доказательство XXI века» (PDF) . Журнал теории и приложений с фиксированной точкой . 11 : 43–63. дои : 10.1007/s11784-012-0071-6 . ISSN 1661-7738 . S2CID 121557270 . Проверено 23 мая 2015 г.
- ^ Орстрем, Питер; Хасле, Пер (1995). «3.7 Временная логика и информатика». Временная логика: от древних идей к искусственному интеллекту . Исследования в области лингвистики и философии. Том. 57. Спрингер Нидерланды . стр. 344–365. дои : 10.1007/978-0-585-37463-5 . ISBN 978-0-7923-3586-3 .
- ^ Лэмпорт, Лесли . «Сочинения Лесли Лэмпорт: Доказательство корректности многопроцессных программ» . Проверено 22 мая 2015 г.
- ^ Лэмпорт, Лесли . «Сочинения Лесли Лэмпорт: сбор мусора на лету: упражнение в сотрудничестве» . Проверено 22 мая 2015 г.
- ^ Лэмпорт, Лесли . «Сочинения Лесли Лэмпорт: «Когда-нибудь» — это иногда «Не никогда» » . Проверено 22 мая 2015 г.
- ^ Jump up to: а б Лэмпорт, Лесли . «Сочинения Лесли Лэмпорт: определение модулей параллельного программирования» . Проверено 22 мая 2015 г.
- ^ Лэмпорт, Лесли . «Сочинения Лесли Лэмпорт: Временная логика действий» . Проверено 22 мая 2015 г.
- ^ Jump up to: а б Ю, Юань; Манолиос, Панайотис; Лэмпорт, Лесли (1999). «Проверка модели TLA + Спецификации». Правильные методы проектирования и проверки аппаратного обеспечения (PDF) . Конспекты лекций по информатике. Том 1703. Springer-Verlag . С. 54–66. doi : 10.1007/3-540-48153-2_6 . ISBN 978-3-540-66559-5 . Проверено 14 мая 2015 г.
- ^ Лэмпорт, Лесли (18 июня 2002 г.). Спецификация систем: TLA + Язык и инструменты для инженеров аппаратного и программного обеспечения . Аддисон-Уэсли . ISBN 978-0-321-14306-8 .
- ^ Лэмпорт, Лесли (2 января 2009 г.). «Язык алгоритмов PlusCal» (PDF) . Теоретические аспекты информатики — ICTAC 2009 . Конспекты лекций по информатике. Том. 5684. Шпрингер Берлин Гейдельберг . стр. 36–60. дои : 10.1007/978-3-642-03466-4_2 . ISBN 978-3-642-03465-7 . Проверено 10 мая 2015 г.
- ^ Jump up to: а б с д Кузино, Дени; Долигез, Дэмиен; Лэмпорт, Лесли ; Мерц, Стефан; Рикеттс, Дэниел; Ванцетто, Эрнан (1 января 2012 г.). «Т.Л.А. + Доказательства». FM 2012: Формальные методы (PDF) . Конспекты лекций по информатике. Том 7436. Springer Berlin Heidelberg . стр. 147–154. doi : 10.1007/978-3-642-32759-9_14 . ISBN 978-3-642-32758-2 . S2CID 5243433 . Проверено 14 мая 2015 г.
- ^
Лэмпорт, Лесли (18 июня 2002 г.). «8.9.2 Закрытие машины» . Спецификация систем: TLA + Язык и инструменты для инженеров аппаратного и программного обеспечения . Аддисон-Уэсли . п. 112. ИСБН 978-0-321-14306-8 .
Мы редко хотим писать спецификацию, которая не является машинно-закрытой. Если мы и пишем его, то обычно это происходит по ошибке.
- ^
Лэмпорт, Лесли (18 июня 2002 г.). «8.9.6 Темпоральная логика считается запутанной» . Спецификация систем: TLA + Язык и инструменты для инженеров аппаратного и программного обеспечения . Аддисон-Уэсли . п. 116. ИСБН 978-0-321-14306-8 .
Действительно, [большинство инженеров] вполне могут обойтись спецификациями вида (8.38), которые выражают только свойства безопасности и не скрывают никаких переменных.
- ^
Маркус А. Куппе (3 июня 2014 г.). Распространенная TLC (запись технических переговоров). TLA + Общественное мероприятие 2014, Тулуза, Франция.
{{cite AV media}}: CS1 maint: местоположение ( ссылка ) - ^ «Неподдерживаемые функции TLAPS» . TLA + Система доказательств . исследований Microsoft и INRIA Совместный центр . Проверено 14 мая 2015 г.
- ^ Кутанов, Эмиль (12 июля 2021 г.). «Spire: совместное фазово-симметричное решение для распределенного консенсуса» . Доступ IEEE . 9 . IEEE : 101702–101717. Бибкод : 2021IEEA...9j1702K . дои : 10.1109/ACCESS.2021.3096326 . S2CID 236480167 .
- ^ ПРИХОДИТЕ + Система доказательств
- ^ Лесли Лэмпорт (3 апреля 2014 г.). Мышление для программистов (21:46) (Запись технического разговора). Сан-Франциско: Microsoft . Проверено 14 мая 2015 г.
- ^ Крис, Ньюкомб (2014). «Почему Amazon выбрала TLA + ". Абстрактные конечные автоматы, сплав, B, TLA, VDM и Z. Конспекты лекций по информатике. Том 8477. Springer Berlin Heidelberg . стр. 25–39. doi : 10.1007/978-3-662-43652-3_3 .ISBN 978-3-662-43651-6 .
- ^ Лардинуа, Фредерик (10 мая 2017 г.). «С помощью Cosmos DB Microsoft хочет создать одну базу данных, которая будет управлять ими всеми» . ТехКранч . Проверено 10 мая 2017 г.
- ^ Лесли Лэмпорт (10 мая 2017 г.). Основы Azure Cosmos DB с доктором Лесли Лэмпорт (запись интервью). Microsoft Azure . Проверено 10 мая 2017 г.
Внешние ссылки
[ редактировать ]- Домашняя страница TLA , веб-страница Лесли Лэмпорт со ссылкой на TLA. + инструменты и ресурсы
- ТЛА + Гиперкнига , ПРИХОДИТ + учебник Лесли Лэмпорт
- Как веб-службы Amazon используют формальные методы , статья в журнале ACM за апрель 2015 г.
- «Думая для программистов» , выступление Лесли Лэмпорт на Build 2014
- Думая над кодом , выступление Лесли Лэмпорт на саммите исследовательского факультета Microsoft в 2014 году
- Кто строит небоскреб, не рисуя чертежи? , выступление Лесли Лэмпорт на React San Francisco 2014
- «Программирование должно быть больше, чем кодирование» , доклад в Стэнфорде в 2015 году. Лесли Лэмпорта
- Евклид пишет алгоритм: сказка , TLA + вступление Лесли Лэмпорта включено в праздничный сборник Манфреда Броя
- ТЛА + Группа Google



