Теорема Нильсена-Шрайера

В теории групп , разделе математики, теорема Нильсена-Шрайера утверждает, что каждая подгруппа сама свободной группы по себе свободна. ^[1]^[2]^[3] Он назван в честь Якоба Нильсена и Отто Шрайера .

Формулировка теоремы

Свободная группа может быть определена из представления группы, состоящего из набора образующих без отношений. То есть каждый элемент является произведением некоторой последовательности образующих и обратных им, но эти элементы не подчиняются никаким уравнениям, кроме тех, которые тривиально следуют из $gg -1$ = 1. Элементы свободной группы можно описать как все возможные сокращенные слова , те строки образующих и их обратных, в которых ни один образующий не является смежным со своим собственным обратным. Два сокращенных слова можно умножить, объединив их, а затем удалив любые пары, обратные генератору, возникающие в результате объединения.

Теорема Нильсена -Шрайера утверждает, что если H является подгруппой свободной группы G , то H сама изоморфна свободной группе. То есть существует множество S элементов, порождающих , без нетривиальных отношений между элементами S. H

Формула Нильсена–Шрайера , или формула индекса Шрайера , количественно определяет результат в случае, когда подгруппа имеет конечный индекс: если G — свободная группа ранга n (свободная от n образующих), а H — подгруппа конечного индекса [ G : H ] = e , то H не имеет ранга $1+e(n{-}1)$ . ^[4]

Пример

Пусть G — свободная группа с двумя образующими $a,b$ , и пусть H — подгруппа, состоящая из всех приведенных слов четной длины (произведений четного числа букв $a,b,a^{-1},b^{-1}$ ). Тогда H порождается своими шестью элементами $p=aa,\ q=ab,\ r=ba,\ s=bb,\ t=ab^{-1},\ u=a^{-1}b.$ Факторизация любого приведенного слова из H на эти образующие и обратные им может быть построена просто путем взятия последовательных пар букв в сокращенном слове. Однако это не свободное представление H , поскольку последние три генератора можно записать через первые три как $s=rp^{-1}q,\ t=pr^{-1},\ u=p^{-1}q$ . Скорее, H порождается как свободная группа тремя элементами $p=aa,\ q=ab,\ r=ba,$ которые не имеют между собой никаких отношений; или вместо этого несколькими другими тройками из шести образующих. ^[5] Далее, G свободен на n = 2 генераторах, H имеет индекс e = [ G : H ] = 2 в G и H свободен на 1 + e ( n –1) = 3 генераторах. Теорема Нильсена-Шрайера утверждает, что, как и H , каждая подгруппа свободной группы может быть порождена как свободная группа, и если индекс H конечен, ее ранг задается формулой индекса.

Доказательство

Свободная группа G = π ₁ ( X ) имеет n соответствующих петлям a , b из базовой точки P в X. = 2 образующих , Подгруппа H слов четной длины с индексом e = [ G : H ] = 2 соответствует покрывающему графу Y с двумя вершинами, соответствующими смежным классам H и H' = aH = bH = a ⁻¹Ч = *б ⁻*¹H и два приподнятых ребра для каждого из исходных ребер петли a , b . Стягивание одного из ребер Y дает гомотопическую эквивалентность букету из трех окружностей, так что H = π ₁ ( Y ) — свободная группа с тремя образующими, например aa , ab , ba .

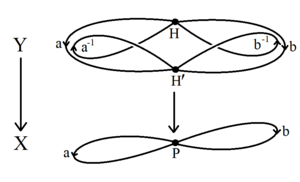
Краткое доказательство теоремы Нильсена-Шрайера использует алгебраическую топологию фундаментальных групп и накрывающих пространств . ^[1] Свободная группа G на множестве образующих — это фундаментальная группа букета окружностей , топологического графа X с единственной вершиной и петлевым ребром для каждого образующего. ^[6] Любая подгруппа H фундаментальной группы сама по себе является фундаментальной группой связного накрывающего пространства Y → X. Пространство Y представляет собой (возможно, бесконечный) топологический граф, граф смежных классов Шрайера, имеющий одну вершину для каждого смежного класса в G/H . ^[7] В любом связном топологическом графе можно сжать ребра остовного дерева графа, создав букет окружностей, имеющих одну и ту же фундаментальную группу H . Поскольку H — фундаментальная группа букета кругов, она сама свободна. ^[6]

Ранг H можно вычислить, используя два свойства эйлеровой характеристики , которые непосредственно следуют из ее определения. Первое свойство состоит в том, что эйлерова характеристика букета из s кругов равна 1 - s . Второе свойство — мультипликативность в накрывающих пространствах : если Y степени d — покрытие X , то

$\chi (Y)=d\cdot \chi (X)$ .

Теперь предположим, что H — подгруппа свободной группы G с индексом [G:H] = e . Предыдущая часть доказательства показывает, что H — свободная группа; пусть r обозначает ранг H . Применение двух свойств эйлеровой характеристики для покрывающего графа Y, соответствующего H, дает следующее:

$\chi (Y)=1-r$

и

$\chi (Y)=e\cdot \chi (X)=e(1-n).$

Объединив эти уравнения, получим $r=1-e(1-n)=1+e(n-1).$

Это доказательство появляется в Мэй «Кратком курсе» . ^[8]Эквивалентное доказательство с использованием гомологии и первого числа Бетти Y принадлежит Рейнхольду Баеру и Фридриху Леви ( 1936 ).Оригинальное доказательство Шрайера формирует граф Шрайера другим способом как фактор графа Кэли группы по $G$ модулю действия $H$ . ^[9]

Согласно лемме о подгруппе Шрайера , набор генераторов для свободного представления $H$ может быть построен из циклов в покрывающем графе, образованном путем объединения пути остовного дерева от базовой точки (смежного класса идентичности) до одного из смежных классов, одно ребро, не являющееся деревом, и обратный путь связующего дерева от другой конечной точки ребра обратно к базовой точке. ^[10]^[9]

Аксиоматические основы

Хотя известно несколько различных доказательств теоремы Нильсена-Шрайера, все они зависят от выбранной аксиомы . Например, в доказательстве, основанном на фундаментальных группах букетов, аксиома выбора появляется под видом утверждения о том, что каждый связный граф имеет остовное дерево. Использование этой аксиомы необходимо, поскольку существуют модели теории множеств Цермело – Френкеля , в которых и выбранная аксиома, и теорема Нильсена – Шрайера неверны. Теорема Нильсена-Шрайера, в свою очередь, подразумевает более слабую версию аксиомы выбора для конечных множеств. ^[11]^[12]

История

Теорема Нильсена-Шрайера является неабелевым аналогом более старого результата Рихарда Дедекинда о том, что каждая подгруппа свободной абелевой группы является свободной абелевой . ^[3]

Якоб Нильсен ( 1921 ) первоначально доказал ограниченную форму теоремы, заявив, что любая конечно порожденная подгруппа свободной группы свободна. Его доказательство включает в себя выполнение последовательности преобразований Нильсена над порождающим набором подгруппы, которые уменьшают их длину (как сокращенные слова в свободной группе, из которой они взяты). ^[1]^[13] Отто Шрайер доказал теорему Нильсена-Шрайера во всей ее общности в своей докторской диссертации , 1926 года «Подгруппы свободной группы» также опубликованной в 1927 году в журнале Abh. Гамбург. Университет ^[14]^[15]

Топологическое доказательство, основанное на фундаментальных группах букетов окружностей, принадлежит Рейнхольду Баеру и Фридриху Леви ( 1936 ). Другое топологическое доказательство, основанное на теории Басса-Серра о действиях групп на деревьях , было опубликовано Жан-Пьером Серром ( 1970 ). ^[16]

См. также

Фундаментальная теорема о циклических группах , аналогичный результат для циклических групп , который в бесконечном случае можно рассматривать как частный случай теоремы Нильсена – Шрайера.
Теорема о подгруппе Куроша

Примечания

^ Перейти обратно: ^а ^б ^с Стиллвелл (1993) , раздел 2.2.4, Теорема Нильсена – Шрайера, стр. 103–104.
^ Магнус, Каррасс и Солитар 1976 , следствие 2.9, с. 95.
^ Перейти обратно: ^а ^б Джонсон (1980) , Раздел 2, Теорема Нильсена – Шрайера, стр. 9–23.
^ Фрид и Джарден (2008) , с. 355
^ Джонсон (1997) , бывш. 15, с. 12.
^ Перейти обратно: ^а ^б Стиллвелл (1993) , раздел 2.1.8, Свобода генераторов, с. 97.
^ Стиллвелл (1993) , Раздел 2.2.2, Свойство подгруппы, стр. 100–101.
^ Мэй, Дж. Питер (1999). «Раздел 4.5». Краткий курс алгебраической топологии (PDF) . Издательство Чикагского университета. ISBN 9780226511832 .
^ Перейти обратно: ^а ^б Боллобас, Бела (1998). «Глава VIII.1». Современная теория графов . Спрингер Верлаг. п. 262. ИСБН 978-0-387-98488-9 .
^ Стиллвелл (1993) , Раздел 2.2.6, Трансверсали Шрайера, стр. 105–106.
^ Ляухли (1962)
^ Ховард (1985) .
^ Магнус, Каррасс и Солитар, 1976 , Раздел 3.2, Процесс восстановления, стр. 121–140.
^ О'Коннор, Джон Дж.; Робертсон, Эдмунд Ф. , «Отто Шрайер» , Архив истории математики MacTutor , Университет Сент-Эндрюс
^ Хансен, Вагн Лундсгаард (1986), Якоб Нильсен, Сборник математических статей: 1913–1932 , Биркхойзер, стр. 117, ISBN. 978-0-8176-3140-6 .
^ Ротман (1995) , Теорема Нильсена – Шрайера, стр. 383–387.

Ссылки

Баер, Рейнхольд ; Леви, Фридрих (1936), «Свободные продукты и их подгруппы», Compositio Mathematica , 3 : 391–398 .
Фрид, Майкл Д .; Жарден, Моше (2008), Полевая арифметика , результаты математики и ее границы. 3-я серия, том. 11 (3-е изд.), Springer-Verlag , с. 70, ISBN 978-3-540-77269-9 , Збл 1145.12001 .
Ховард, Пол Э. (1985), «Подгруппы свободной группы и аксиома выбора», Журнал символической логики , 50 (2): 458–467, doi : 10.2307/2274234 , JSTOR 2274234 , MR 0793126 , S2CID 33535673 .
Джонсон, Д.Л. (1980), Темы теории групповых представлений , серия лекций Лондонского математического общества, том. 42, Издательство Кембриджского университета, ISBN 978-0-521-23108-4 .
Джонсон, Д.Л. (1997), «Презентации групп» , студенческие тексты Лондонского математического общества, том. 15 (2-е изд.), Издательство Кембриджского университета, ISBN 978-0-521-58542-2 .
Ляухли, Ганс (1962), «Auswahlaxiom in der Algebra», Commentarii Mathematici Helvetici , 37 : 1–18, doi : 10.1007/bf02566957 , hdl : 20.500.11850/131689 , MR 0143705 , S2CID 1862 23589 .
Магнус, Вильгельм ; Каррасс, Авраам; Солитар, Дональд (1976), Комбинаторная теория групп (2-е исправленное издание), Dover Publications .
Нильсен, Якоб (1921), «Об исчислении с некоммутативными факторами и его применении к теории групп», Math. Журнал B (на датском языке), 1921 : 78–94, JFM 48.0123.03 .
Ротман, Джозеф Дж. (1995), Введение в теорию групп , Тексты для аспирантов по математике, том. 148 (4-е изд.), Springer-Verlag, ISBN 978-0-387-94285-8 .
Серр, Ж.-П. (1970), Дискретные группы , отрывок из ежегодника Колледжа де Франс, Париж. {{citation}}: CS1 maint: отсутствует местоположение издателя ( ссылка ) .
Серр, Ж.-П. (1980), Деревья , Springer-Verlag, ISBN 3-540-10103-9 .
Стиллвелл, Джон (1993), Классическая топология и комбинаторная теория групп , Тексты для аспирантов по математике, том. 72 (2-е изд.), Springer-Verlag .

[stillwell-1] Перейти обратно: ^а ^б ^с Стиллвелл (1993) , раздел 2.2.4, Теорема Нильсена – Шрайера, стр. 103–104.

[2] Магнус, Каррасс и Солитар 1976 , следствие 2.9, с. 95.

[j80-3] Перейти обратно: ^а ^б Джонсон (1980) , Раздел 2, Теорема Нильсена – Шрайера, стр. 9–23.

[4] Фрид и Джарден (2008) , с. 355

[5] Джонсон (1997) , бывш. 15, с. 12.

[still-bouquet-6] Перейти обратно: ^а ^б Стиллвелл (1993) , раздел 2.1.8, Свобода генераторов, с. 97.

[7] Стиллвелл (1993) , Раздел 2.2.2, Свойство подгруппы, стр. 100–101.

[8] Мэй, Дж. Питер (1999). «Раздел 4.5». Краткий курс алгебраической топологии (PDF) . Издательство Чикагского университета. ISBN 9780226511832 .

[:0-9] Перейти обратно: ^а ^б Боллобас, Бела (1998). «Глава VIII.1». Современная теория графов . Спрингер Верлаг. п. 262. ИСБН 978-0-387-98488-9 .

[10] Стиллвелл (1993) , Раздел 2.2.6, Трансверсали Шрайера, стр. 105–106.

[11] Ляухли (1962)

[12] Ховард (1985) .

[13] Магнус, Каррасс и Солитар, 1976 , Раздел 3.2, Процесс восстановления, стр. 121–140.

[14] О'Коннор, Джон Дж.; Робертсон, Эдмунд Ф. , «Отто Шрайер» , Архив истории математики MacTutor , Университет Сент-Эндрюс

[15] Хансен, Вагн Лундсгаард (1986), Якоб Нильсен, Сборник математических статей: 1913–1932 , Биркхойзер, стр. 117, ISBN. 978-0-8176-3140-6 .

[rotman-16] Ротман (1995) , Теорема Нильсена – Шрайера, стр. 383–387.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]