Олог

Теория логов — это попытка предоставить строгую математическую основу для представления знаний, построения научных моделей и хранения данных с использованием теории категорий , лингвистических и графических инструментов. Ологи были представлены в 2012 году Дэвидом Спиваком и Робертом Кентом. ^[1]

Этимология [ править ]

Термин «олог» является сокращением от « журнал онтологии ». «Онтология» происходит от онто- , от греческого ὤν , ὄντος «бытие; то, что есть», причастия настоящего времени глагола εἰμί «быть», и -λογία , -logia : наука , исследование , теория .

Математический формализм [ править ]

Змея ${\mathcal {C}}$ для данного домена - это категория которой , объекты представляют собой блоки, помеченные фразами (точнее, неопределенными именными фразами в единственном числе), относящимися к домену, и чьи морфизмы представляют собой направленные стрелки между блоками, помеченными глагольными фразами, также относящимися к домену. Эти существительные и глагольные фразы объединяются в предложения, которые выражают отношения между объектами в предметной области.

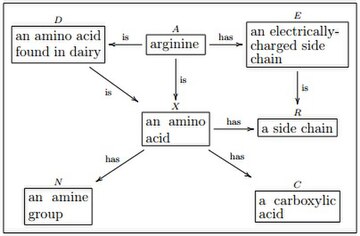
В каждом журнале объекты существуют в пределах целевой категории . Если не указано иное, целевой категорией считается ${\textbf {Set}}$ , категория множеств и функций .Поля на диаграмме выше представляют собой объекты ${\textbf {Set}}$ . Например, блок, содержащий фразу «аминокислота», представляет набор всех аминокислот, а блок, содержащий фразу «боковая цепь», представляет набор всех боковых цепей. Стрелка с надписью «имеет», указывающая от «аминокислоты» к «боковой цепи», представляет функцию, которая сопоставляет каждую аминокислоту с ее уникальной боковой цепью.

Другая целевая категория, которую можно использовать, — это категория Клейсли. ${\mathcal {C}}_{\mathbb {P} }$ мощности монады набора . Учитывая $A\in Ob({\textbf {Set}})$ , $\mathbb {P} (A)$ тогда это степенной набор A. Естественное преобразование $\eta$ карты $a\in A$ к синглтону $\{a\}$ и естественное преобразование $\mu$ отображает набор множеств в его объединение. Категория Клейсли ${\mathcal {C}}_{\mathbb {P} }$ категория, в которой объекты соответствуют объектам в $\mathbb {P}$ и морфизмы, устанавливающие бинарные отношения . Учитывая морфизм $f:A\to B$ , и учитывая $a\in A$ и $b\in B$ , определим морфизм $R$ сказав это $(a,b)\in R$ в любое время $b\in f(a)$ . Глагольные фразы, используемые с этой целевой категорией, должны иметь смысл с объектами, которые являются подмножествами: например, «относится к» или «больше чем».

Другая возможная целевая категория — это категория вероятностных распределений Клейсли, называемая монадой Жири. ^[2] Это обеспечивает обобщение марковских процессов принятия решений .

Ологи и базы данных [ править ]

Змея ${\mathcal {C}}$ также можно рассматривать как схему базы данных . Каждая коробка (предмет ${\mathcal {C}}$ ) в логе есть таблица $T$ а стрелки (морфизмы), исходящие из прямоугольника, являются столбцами в ${\mathcal {C}}$ . Присвоение конкретного экземпляра объекту ${\mathcal {C}}$ делается через функтор $I:{\mathcal {C}}\to {\textbf {Set}}$ . В приведенном выше примере поле «аминокислота» будет представлено в виде таблицы, количество строк которой равно количеству типов аминокислот, а количество столбцов равно трем, по одному столбцу на каждую стрелку, исходящую из этого поля.

Отношения между ологами [ править ]

«Связь» между разными ологами, которая на практике может быть связью между разными моделями или мировоззрениями, осуществляется с помощью функторов . Спивак вводит понятия «значимых» и «сильно значимых» функторов. ^[1] Позволять ${\mathcal {C}}$ и ${\mathcal {D}}$ быть двумя ологами, $I:{\mathcal {C}}\to {\textbf {Set}}$ , $J:{\mathcal {D}}\to {\textbf {Set}}$ функторы (см. раздел о логах и базах данных) и $F:{\mathcal {C}}\to {\mathcal {D}}$ функтор. $F$ называется отображением схемы . Мы говорим, что $F$ имеет смысл , если существует естественное преобразование $m:I\to F^{*}J$ ( откат J посредством F).

Взяв за пример ${\mathcal {C}}$ и ${\mathcal {D}}$ как две разные научные модели, функтор $F$ имеет смысл, если «предсказания», которые являются объектами в ${\textbf {Set}}$ , сделанный по первой модели ${\mathcal {C}}$ можно перевести на вторую модель ${\mathcal {D}}$ .

Мы говорим, что $F$ имеет большое значение, если задан объект $X\in {\mathcal {C}}$ у нас есть $I(X)=J(F(X))$ . Это равенство эквивалентно требованию $m$ быть естественным изоморфизмом.

Иногда бывает трудно найти значимый функтор $F$ от ${\mathcal {C}}$ к ${\mathcal {D}}$ . В таком случае мы можем попытаться определить новый лог ${\mathcal {B}}$ который представляет собой общую основу ${\mathcal {C}}$ и ${\mathcal {D}}$ и найти значимые функторы $F_{\mathcal {C}}:{\mathcal {B}}\to {\mathcal {C}}$ и $F_{\mathcal {D}}:{\mathcal {B}}\to {\mathcal {D}}$ .

Если связь между ологами ограничивается двусторонней связью, как описано выше, тогда мы можем думать о совокупности логов как об узлах графа , а о ребрах как о функторах, соединяющих ологов. Если разрешена одновременная связь между более чем двумя ологами, то граф становится симметричным симплициальным комплексом .

Правила добросовестной практики [ править ]

Спивак дает некоторые правила хорошей практики написания лога, морфизмы которого имеют функциональную природу (см. первый пример в разделе «Математический формализм»). ^[1] Текст в рамке должен соответствовать следующим правилам:

начинаются со слова «а» или «ан». (Пример: «аминокислота»).
относятся к различию, сделанному и узнаваемому автором олога.
относятся к различию, для которого существует четко определенный функтор, диапазон которого равен ${\textbf {Set}}$ , т.е. экземпляр может быть задокументирован. (Пример: есть набор всех аминокислот).
объявите все переменные в составной структуре. (Пример: вместо написания в графе «мужчина и женщина» напишите «мужчина». $m$ и женщина $w$ "или" пара $(m,w)$ где $m$ это мужчина и $w$ это женщина»).

Первые три правила гарантируют, что объекты (блоки), определенные автором журнала, представляют собой четко определенные наборы. Четвертое правило улучшает маркировку стрелок в логе.

Приложения [ править ]

Эта концепция была использована в статье Дэвида Спивака и других, опубликованной в декабрьском номере журнала BioNanoScience за 2011 год , чтобы установить научную аналогию между паучьим шелком и музыкальной композицией. ^[3]

См. также [ править ]

Ссылки [ править ]

^ Jump up to: Перейти обратно: ^а ^б ^с Спивак, Дэвид И.; Кент, Роберт Э. (31 января 2012 г.). «Ологи: категориальная основа представления знаний» . ПЛОС ОДИН . 7 (1): e24274. arXiv : 1102.1889 . Бибкод : 2012PLoSO...724274S . дои : 10.1371/journal.pone.0024274 . ПМК 3269434 . ПМИД 22303434 .
^ Монада Гири в n Lab
^ Гиза, Тристан; Спивак, Дэвид И.; Бюлер, Маркус Дж. (2011). «Повторяющиеся закономерности в иерархических белковых материалах и музыке: сила аналогий». Бионанонаука . 1 (4): 153–161. arXiv : 1111.5297 . дои : 10.1007/s12668-011-0022-5 . S2CID 5178100 .

Внешние ссылки [ править ]

Спивак, Давид И. «Категорическая информатика» . math.mit.edu . Проверено 2 мая 2017 г.
Спивак, Дэвид И. (2014). Теория категорий для наук . Кембридж, Массачусетс: MIT Press . ISBN 9780262028134 . OCLC 876833252 .

[Spivak-1] Jump up to: Перейти обратно: ^а ^б ^с Спивак, Дэвид И.; Кент, Роберт Э. (31 января 2012 г.). «Ологи: категориальная основа представления знаний» . ПЛОС ОДИН . 7 (1): e24274. arXiv : 1102.1889 . Бибкод : 2012PLoSO...724274S . дои : 10.1371/journal.pone.0024274 . ПМК 3269434 . ПМИД 22303434 .

[2] Монада Гири в n Lab

[3] Гиза, Тристан; Спивак, Дэвид И.; Бюлер, Маркус Дж. (2011). «Повторяющиеся закономерности в иерархических белковых материалах и музыке: сила аналогий». Бионанонаука . 1 (4): 153–161. arXiv : 1111.5297 . дои : 10.1007/s12668-011-0022-5 . S2CID 5178100 .

[1]

[2]

[3]