Схематическое рассуждение

Схематическое рассуждение – это рассуждение посредством визуальных представлений . Изучение схематического рассуждения связано с пониманием концепций и идей, визуализируемых с использованием диаграмм и образов, а не лингвистическими или алгебраическими средствами.

Диаграмма

Диаграмма — это двумерное геометрическое символическое представление информации в соответствии с некоторой техникой визуализации . Иногда в этом методе используется 3D- визуализация, которая затем проецируется на 2D-поверхность. Термин диаграмма в здравом смысле может иметь два значения.

Пример блок-схемы, представляющей процесс принятия решения о добавлении новой статьи в Википедию.

• Устройство визуальной информации : Как и термин « иллюстрация », диаграмма используется как собирательный термин, обозначающий целый класс технических жанров, включая графики , технические чертежи и таблицы .
• особый вид визуального отображения : это всего лишь жанр, который показывает качественные данные в виде фигур, соединенных линиями, стрелками или другими визуальными связями.

В науке этот термин используется в обоих смыслах. Например, Андерсон (1997) заявил в более общем плане: «Диаграммы представляют собой графические, но абстрактные представления информации, а карты , линейные графики , гистограммы , инженерные чертежи и архитекторов эскизы — все это примеры диаграмм, тогда как фотографии и видео не являются примерами диаграмм». ". С другой стороны, Лоу (1993) определил диаграммы как «абстрактные графические изображения предмета, который они представляют».

В конкретном смысле диаграммы и диаграммы противопоставляют компьютерную графику , технические иллюстрации, инфографику , карты и технические чертежи , показывая «абстрактное, а не буквальное представление информации». Суть диаграммы можно рассматривать как:

• форма устройств визуального форматирования ​
• дисплей , который отображает не количественные данные , а отношения и абстрактную информацию.
• со строительными блоками , такими как геометрические фигуры, соединенные линиями , стрелками или другими визуальными связями.

Или, как писал Берт С. Холл, «диаграммы — это упрощенные фигуры, в некотором смысле карикатуры, призванные передать основной смысл». По словам Яна В. Уайта (1984), «характеристиками хорошей диаграммы являются элегантность, ясность, легкость, закономерность, простота и достоверность». Элегантность для белого означает, что то, что вы видите на диаграмме, является «самым простым и подходящим решением проблемы».

Логический график

Логический граф — это особый тип теоретико-графовой структуры в любой из нескольких систем графического синтаксиса , которые Чарльз Сандерс Пирс разработал для логики .

В своих статьях о качественной логике , энтитативных графах и экзистенциальных графах Пирс разработал несколько версий графического формализма или теоретико-графового формального языка , предназначенного для интерпретации в логике.

За столетие, прошедшие с тех пор, как Пирс начал эту линию развития, на основе абстрактно одной и той же формальной основы теоретико-графовых структур развилось множество формальных систем.

график

( Концептуальный граф CG) — это обозначение логики, основанное на экзистенциальных графах Чарльза Сандерса Пирса и семантических сетях искусственного интеллекта . В первой опубликованной статье о концептуальных графах Джон Ф. Сова использовал их для представления концептуальных схем, используемых в системах баз данных. Его первая книга применил их к широкому кругу тем в области искусственного интеллекта, информатики и когнитивной науки. Линейная нотация, называемая форматом обмена концептуальными графами (CGIF) , была стандартизирована в стандарте ISO для общей логики .

Кошка Элси сидит на коврике

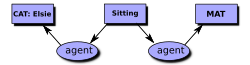
Диаграмма справа представляет собой пример формы отображения концептуального графика. Каждый блок называется узлом понятий , а каждый овал — узлом отношений . В CGIF эта CG будет представлена ​​следующим утверждением:

[Кот Элси] [Сидит *x] [Мэт *y] (агент ?x Элси) (локация ?x ?y)

В CGIF скобки заключают информацию внутри узлов понятий, а круглые скобки заключают информацию внутри узлов отношений. Буквы x и y, называемые метками кореференции , показывают, как связаны между собой узлы понятия и отношения. В формате Common Logic Interchange Format (CLIF) эти буквы сопоставляются с переменными, как в следующем операторе:

(существует ((x Сидит) (y Мат)) (и (Кот Элси) (агент x Элси) (локация xy)))

Как показано в этом примере, звездочки на метках кореференции *x и *y в CGIF соответствуют экзистенциально квантифицированным переменным в CLIF, а вопросительные знаки на ?x и ?y соответствуют связанным переменным в CLIF. Квантор универсальности, представленный @every*z в CGIF, будет представлен forall (z) в CLIF.

Энтитативный граф

Энтитативный граф — это элемент графического синтаксиса логики , который Чарльз Сандерс Пирс разработал под названием качественной логики, начиная с 1880-х годов, охватывая формализм только в том, что касается пропозициональных или сентенциальных аспектов логики.

Синтаксис ​ :

• Пустая страница;
• Отдельные буквы, фразы;
• Объекты (подграфы), заключенные в простую замкнутую кривую, называемую разрезом . Разрез может быть пустым.

Семантика такова :

• Пустая страница означает False ;
• Буквы, фразы, подграфы и целые графы могут быть True' или False ;
• Окружение объектов разрезом эквивалентно логическому дополнению . Следовательно, пустой разрез обозначает Истину ;
• Все объекты внутри данного разреза неявно соединяются посредством дизъюнкции .

«Доказательство» манипулирует графиком, используя короткий список правил, пока граф не превратится в пустой фрагмент или пустую страницу. Граф, который можно сократить таким образом, теперь называется тавтологией ( или ее дополнением). Графы, которые нельзя упростить до определенной точки, являются аналогами выполнимых формул логики первого порядка .

Экзистенциальный график

Экзистенциальный граф — это тип схематического или визуального обозначения логических выражений, предложенный Чарльзом Сандерсом Пирсом , который написал свою первую статью по графической логике в 1882 году и продолжал развивать этот метод до своей смерти в 1914 году. Пирс предложил три системы экзистенциальных графов. :

• альфа – изоморфна и логике предложений двухэлементной булевой алгебре ;
• бета – изоморфна логике первого порядка с единицей, со всеми закрытыми формулами;
• гамма – (почти) изоморфна нормальной модальной логике .

Альфа гнездится в бета и гамма . Бета не вложена в гамма , квантифицированная модальная логика — это нечто большее, чем мог себе представить даже Пирс.

Альфа-графы

В альфа- синтаксис версии :

• Пустая страница;
• Отдельные буквы или фразы, написанные в любом месте страницы;
• Любой граф может быть заключен в простую замкнутую кривую, называемую разрезом или sep . Разрез может быть пустым. Разрезы могут вкладываться и объединяться по желанию, но никогда не должны пересекаться.

Любая правильно сформированная часть графа является подграфом .

Семантика такова :

• Пустая страница означает Истину ;
• Буквы, фразы, подграфы и целые графики могут быть истинными или ложными ;
• Охват подграфа разрезом эквивалентен логическому отрицанию или логическому дополнению . Следовательно, пустой разрез обозначает False ;
• Все подграфы внутри данного разреза молчаливо соединены .

Следовательно, альфа- графики представляют собой минималистскую систему обозначений логики предложений , основанную на выразительной адекватности «И» и « Не» . Альфа - графы представляют собой радикальное упрощение двухэлементной булевой алгебры и функторов истинности .

Универсальные характеристики

Характеристика Universalis , обычно интерпретируемая как универсальная характеристика или универсальный характер на английском языке, представляет собой универсальный и формальный язык, придуманный немецким философом Готфридом Лейбницем, способный выражать математические, научные и метафизические концепции. Таким образом, Лейбниц надеялся создать язык, который можно было бы использовать в рамках универсальных логических вычислений или рассудочного исчисления .

Схематическое рассуждение Лейбница.

Поскольку универсальная характеристика схематична и использует пиктограммы (внизу слева), диаграммы в работах Лейбница заслуживают внимательного изучения. По крайней мере в двух случаях Лейбниц иллюстрировал свои философские рассуждения диаграммами. Одна из диаграмм, фронтиспис его книги «De Arte Combinatoria» («Об искусстве комбинаций») 1666 года, представляет собой аристотелевскую теорию о том, как все материальные вещи образуются из комбинаций элементов земли, воды, воздуха и огня.

Основные элементы пиктограмм Лейбница.

Эти четыре элемента составляют четыре угла ромба (см. рисунок справа). Противостоящие пары из них соединены перемычкой с надписью «противоположности» (земля-воздух, огонь-вода). В четырех углах наложенного квадрата находятся четыре качества, определяющие элементы. Каждая соседняя пара из них соединена полосой с надписью «возможная комбинация»; соединяющие их диагонали обозначены как «невозможная комбинация». Начиная сверху, огонь образуется из сочетания сухости и тепла; воздух от сырости и тепла; вода от холода и сырости; землю от холода и сухости.

Система рассуждений Венн-II

В начале 1990-х годов Сун-Джу Шин представил расширение экзистенциальных графов под названием Venn-II. Синтаксис и семантика даны формально вместе с набором правил трансформации , которые показаны как обоснованные и полные. Доказательства продолжаются путем последовательного применения правил (которые удаляют или добавляют синтаксические элементы в диаграммы или из них). Венн-II по выразительной силе эквивалентен монадическому языку первого порядка.

См. также

• Эвристика
• Как решить эту проблему Джордж Полиа
• Естественный вычет
• Пропозициональное исчисление
• Пространственно-временное рассуждение
• Триконик
• Визуальное рассуждение

Дальнейшее чтение

• Джерард Оллвейн и Джон Барвайз (редактор) (1996). Логические рассуждения с помощью диаграмм . Издательство Оксфордского университета.
• Майкл Андерсон, Питер Ченг, Волкер Хаарслев (ред.) (2000). Теория и применение диаграмм: Первая международная конференция «Диаграммы», 2000 г. Эдинбург, Шотландия, Великобритания, 1–3 сентября 2000 г. Материалы.
• Майкл Андерсон и Р. Маккартни (2003). Обработка диаграмм: вычисления с диаграммами . В: Искусственный интеллект , том 145, выпуск 1–2, апрель 2003 г.
• Джеймс Роберт Браун (1999). Философия математики: введение в мир доказательств и изображений . Рутледж.
• Джеймс Франклин (2000). Схематическое рассуждение и моделирование в воображении: секретное оружие научной революции , 1543 г. и «Все это: образ и слово, изменение и преемственность в протонаучной революции» , под ред. Г. Фриланд и А. Коронес (Клувер, Дордрехт), стр. 53–115.
• Дженис Глазго, Н. Хари Нараянан и Б. Чандрасекаран (редактор) (1995). Диаграммное рассуждение: когнитивные и вычислительные перспективы . АААИ Пресс.
• Кульпа, Зенон . « Схематическое изображение и рассуждение ». Машина ГРАФИКА И ВИДЕНИЕ 3 (1/2. 1994.
• Джем Стэплтон Обзор систем рассуждений, основанных на диаграммах Эйлера . Электронные заметки по теоретической информатике. 2005.

Внешние ссылки

• Сайт схематического рассуждения. Архивировано 19 июня 2009 г. в Wayback Machine из Хартфордского университета, Коннектикут, США.
• Лекция об универсальной алгебре и схематических рассуждениях , 3 февраля 2006 г. Джона Баэза
• Группа визуального моделирования в Брайтонском университете, Великобритания.
• Диаграммы Марло онлайн для решения силлогизмов .