Искусственный нейрон

Структура искусственного нейрона

Искусственный нейрон — это математическая функция , задуманная как модель биологических нейронов в нейронной сети . Искусственные нейроны — это элементарные единицы искусственных нейронных сетей . Искусственный нейрон — это функция, которая получает один или несколько входных данных, присваивает этим входным весам веса и суммирует их для получения выходных данных.

Дизайн искусственного нейрона был вдохновлен нейронной схемой . Его входы аналогичны возбуждающим постсинаптическим потенциалам и тормозным постсинаптическим потенциалам нервных дендритов , или активации , его вес аналогичен синаптическому весу нейрона , а его выходной сигнал аналогичен потенциалу действия , который передается по его аксону .

Обычно каждый вход взвешивается отдельно , и сумма часто добавляется к члену, известному как смещение (в общих чертах соответствующее пороговому потенциалу ), прежде чем пройти через нелинейную функцию, известную как функция активации или передаточная функция. . Передаточные функции обычно имеют сигмовидную форму , но могут также принимать форму других нелинейных функций, кусочно -линейных функций или ступенчатых функций . Они также часто монотонно возрастают , непрерывны , дифференцируемы и ограничены . Недавно также были исследованы немонотонные, неограниченные и осциллирующие функции активации с несколькими нулями, которые превосходят сигмоидальные и ReLU-подобные функции активации во многих задачах. Функция определения порога вдохновила на создание логических элементов, называемых пороговой логикой; применимо для построения логических схем, напоминающих обработку мозга. Например, новые устройства, такие как мемристоры . в последнее время для разработки такой логики широко используются

линейной системы Передаточную функцию искусственного нейрона не следует путать с передаточной функцией .

Искусственный нейрон может называться полулинейной единицей , Nv-нейроном , бинарным нейроном , линейной пороговой функцией или МакКаллоха-Питтса ( MCP ) нейроном , в зависимости от используемой структуры.

Простые искусственные нейроны, такие как модель Маккаллоха-Питтса, иногда называют «карикатурными моделями», поскольку они предназначены для отражения одного или нескольких нейрофизиологических наблюдений, но без учета реализма. Искусственные нейроны также могут относиться к искусственным клеткам в нейроморфной инженерии ( см . ниже ), которые похожи на естественные физические нейроны.

Базовая структура

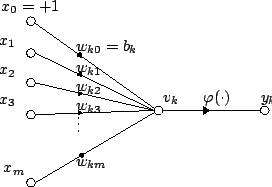
Для данного искусственного нейрона k пусть имеется m + 1 вход с сигналами от x ₀ до x _m и весами от w _{k 0} до w _{k m} . Обычно входу x ₀ присваивается значение +1, что делает его входом смещения с w _{k 0} = b _k . Это оставляет только m фактических входов для нейрона: от x ₁ до x _m .

Выходной сигнал k -го нейрона:

$y_{k}=\varphi \left(\sum _{j=0}^{m}w_{kj}x_{j}\right)$

Где $\varphi$ (phi) — передаточная функция (обычно пороговая функция).

Выходной сигнал аналогичен аксону биологического нейрона, и его значение распространяется на вход следующего слоя через синапс. Он также может выйти из системы, возможно, как часть выходного вектора .

У него нет процесса обучения как такового. Рассчитываются веса его передаточной функции и заранее определяется пороговое значение.

Нейрон Маккаллоха – Питтса (MCP)

См. Также: Персептрон

Нейрон MCP — это своего рода ограниченный искусственный нейрон, который работает с дискретными временными шагами. Каждый из них имеет ноль или более входов и записывается как $x_{1},...,x_{n}$. Он имеет один выход, записанный как $y$. Каждый вход может быть либо возбуждающим , либо тормозящим . Выход может быть либо тихим , либо стреляющим . Нейрон MCP также имеет порог $b\in \{0,1,2,...\}$.

В нейронной сети MCP все нейроны работают синхронно с дискретными временными шагами. $t=0,1,2,3,...$. Во время $t+1$, выход нейрона $y(t+1)=1$ если количество возбуждающих входов по меньшей мере равно порогу и ни один тормозной вход не активируется; $y(t+1)=0$ в противном случае.

Каждый выход может быть входом для произвольного числа нейронов, включая самого себя (то есть возможны циклы). Однако выход не может соединяться с одним нейроном более одного раза. Самоциклы не вызывают противоречий, поскольку сеть работает синхронно с дискретными временными шагами.

В качестве простого примера рассмотрим один нейрон с порогом 0 и одну тормозную петлю. Его выходной сигнал будет колебаться между 0 и 1 на каждом шаге, действуя как «часы».

Любой конечный автомат может быть смоделирован нейронной сетью MCP. Нейронные сети MCP, оснащенные бесконечной лентой, могут моделировать любую машину Тьюринга .

Биологические модели

Основная статья: Модель биологического нейрона

Нейрон и миелинизированный аксон с потоком сигналов от входов дендритов к выходам терминалей аксона.

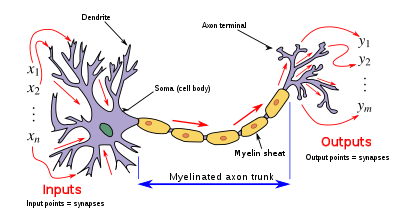
Искусственные нейроны созданы для имитации особенностей своих биологических аналогов. Однако между биологическими и искусственными нейронными сетями существует значительный разрыв в производительности. одиночные биологические нейроны в человеческом мозге с осциллирующей функцией активации, способные обучаться функции XOR . В частности, были обнаружены

• Дендриты . В биологическом нейроне дендриты действуют как входной вектор. Эти дендриты позволяют клетке получать сигналы от большого (>1000) числа соседних нейронов. Как и в приведенной выше математической обработке, каждый дендрит способен выполнять «умножение» на «весовое значение» этого дендрита. Умножение осуществляется за счет увеличения или уменьшения соотношения синаптических нейротрансмиттеров и сигнальных химических веществ, вводимых в дендрит в ответ на синаптический нейромедиатор. Отрицательный эффект мультипликации может быть достигнут за счет передачи ингибиторов сигнала (т.е. противоположно заряженных ионов) по дендриту в ответ на прием синаптических нейротрансмиттеров.
• Сома . В биологическом нейроне сома действует как функция суммирования, как видно из приведенного выше математического описания. Когда положительные и отрицательные сигналы (возбуждающие и тормозящие соответственно) поступают в сому от дендритов, положительные и отрицательные ионы эффективно суммируются просто потому, что смешиваются вместе в растворе внутри тела клетки.
• Аксон . Аксон получает сигнал от процесса суммирования, который происходит внутри сомы. Отверстие аксона, по сути, измеряет электрический потенциал раствора внутри сомы. Как только сома достигает определенного потенциала, аксон передает сигнальный импульс по всей своей длине. В этом отношении аксон выступает для нас как возможность соединять наш искусственный нейрон с другими искусственными нейронами.

Однако, в отличие от большинства искусственных нейронов, биологические нейроны активируются дискретными импульсами. Каждый раз, когда электрический потенциал внутри сомы достигает определенного порога, по аксону передается импульс. Эту пульсацию можно перевести в непрерывные значения. Скорость (активаций в секунду и т. д.), с которой срабатывает аксон, напрямую преобразуется в скорость, с которой соседние клетки получают в себя сигнальные ионы. Чем быстрее срабатывает биологический нейрон, тем быстрее близлежащие нейроны накапливают электрический потенциал (или теряют электрический потенциал, в зависимости от «веса» дендрита, который соединяется с сработавшим нейроном). Именно это преобразование позволяет ученым-компьютерщикам и математикам моделировать биологические нейронные сети с использованием искусственных нейронов, которые могут выдавать разные значения (часто от -1 до 1).

Кодирование

Исследования показали, что унарное кодирование используется в нейронных цепях, ответственных за воспроизведение пения птиц, . Использование унарного кода в биологических сетях, по-видимому, связано с простотой кодирования. Еще одним фактором, способствующим этому, может быть то, что унарное кодирование обеспечивает определенную степень исправления ошибок.

Физические искусственные клетки

Ведутся исследования и разработки в области физических искусственных нейронов – органических и неорганических.

Например, некоторые искусственные нейроны могут получать и высвобождают дофамин ( химические сигналы, а не электрические сигналы) и взаимодействуют с естественными клетками мышц и мозга крысы , что потенциально может быть использовано в BCI / протезировании .

малой мощности Биосовместимые мемристоры могут позволить создавать искусственные нейроны, которые функционируют при напряжениях биологических потенциалов действия и могут использоваться для непосредственной обработки биосенсорных сигналов , для нейроморфных вычислений и/или прямой связи с биологическими нейронами .

Органические нейроморфные схемы, изготовленные из полимеров и покрытые гелем, богатым ионами, позволяющим материалу переносить электрический заряд, как настоящие нейроны , были встроены в робота, что позволяет ему обучаться сенсомоторно в реальном мире, а не посредством моделирования или практически. Более того, искусственные шиповые нейроны, изготовленные из мягкого вещества (полимеров), могут работать в биологически значимых средах и обеспечивать синергетическую связь между искусственными и биологическими доменами.

История

Первым искусственным нейроном был Threshold Logic Unit (TLU), или Linear Threshold Unit. впервые предложена Уорреном Маккалоком и Уолтером Питтсом в 1943 году. Модель была специально разработана как вычислительная модель «нервной сети» в мозге. В качестве передаточной функции использовался порог, эквивалентный использованию ступенчатой ​​функции Хевисайда . Первоначально рассматривалась только простая модель с двоичными входами и выходами, некоторыми ограничениями на возможные веса и более гибким пороговым значением. С самого начала уже было замечено, что любая логическая функция может быть реализована сетями таких устройств, что легко увидеть из того факта, что можно реализовать функции И и ИЛИ и использовать их в дизъюнктивной или конъюнктивной нормальной форме . Исследователи также вскоре поняли, что циклические сети с обратной связью через нейроны могут определять динамические системы с памятью, но большая часть исследований сосредоточилась (и до сих пор делает) на сетях строго прямой связи из- за меньших трудностей, которые они представляют.

Одной из важных и новаторских искусственных нейронных сетей, использовавших линейную пороговую функцию, был персептрон , разработанный Фрэнком Розенблаттом . Эта модель уже учитывала более гибкие значения веса в нейронах и использовалась в машинах с адаптивными возможностями. Представление пороговых значений как фактора смещения было введено Бернардом Уидроу в 1960 году – см. ADALINE .

В конце 1980-х годов, когда исследования нейронных сетей вновь набрали силу, стали рассматриваться нейроны более непрерывной формы. Возможность дифференцирования функции активации позволяет напрямую использовать градиентный спуск и другие алгоритмы оптимизации для корректировки весов. Нейронные сети также начали использоваться в качестве общей модели аппроксимации функций . Самый известный алгоритм обучения, называемый обратным распространением ошибки, был открыт несколько раз, но его первая разработка восходит к работе Пола Вербоса .

Виды передаточных функций

Основная статья: Передаточная функция

Передаточная функция ( функция активации ) нейрона выбирается так, чтобы она имела ряд свойств, которые либо улучшают, либо упрощают сеть, содержащую нейрон. Крайне важно, например, что любой многослойный персептрон, использующий линейную передаточную функцию, имеет эквивалентную однослойную сеть; поэтому для получения преимуществ многоуровневой сети необходима нелинейная функция.

Ниже во всех случаях u относится к взвешенной сумме всех входных данных нейрона, т. е. для n входных данных

$u=\sum _{i=1}^{n}w_{i}x_{i}$

где w — вектор синаптических весов , а x — вектор входов.

Ступенчатая функция

Выход y этой передаточной функции является двоичным, в зависимости от того, соответствует ли вход заданному порогу θ . Посылается «сигнал», т.е. выход устанавливается на единицу, если активация соответствует пороговому значению.

$y={\begin{cases}1&{\text{if }}u\geq \theta \\0&{\text{if }}u<\theta \end{cases}}$

Эта функция используется в персептронах и часто встречается во многих других моделях. Он выполняет деление пространства входов гиперплоскостью . Это особенно полезно на последнем уровне сети, предназначенном для двоичной классификации входных данных. Его можно аппроксимировать на основе других сигмоидальных функций, присвоив весам большие значения.

Линейная комбинация

В этом случае выходная единица представляет собой просто взвешенную сумму ее входов плюс член смещения . Несколько таких линейных нейронов выполняют линейное преобразование входного вектора. Обычно это более полезно на первых уровнях сети. Существует ряд инструментов анализа, основанных на линейных моделях, таких как гармонический анализ , и все они могут использоваться в нейронных сетях с этим линейным нейроном. Термин смещения позволяет нам выполнять аффинные преобразования данных.

См.: Линейное преобразование , Гармонический анализ , Линейный фильтр , Вейвлет , Анализ главных компонент , Анализ независимых компонентов , Деконволюция .

сигмовидная

См. также: Сигмовидная функция.

Довольно простая нелинейная функция, сигмовидная функция, такая как логистическая функция, также имеет легко вычисляемую производную, которая может быть важна при расчете обновлений веса в сети. Таким образом, это делает сеть более легко манипулируемой математически и было привлекательно для первых ученых-компьютерщиков, которым нужно было минимизировать вычислительную нагрузку при моделировании. Ранее это часто наблюдалось в многослойных перцептронах . Однако недавняя работа показала, что сигмовидные нейроны менее эффективны, чем выпрямленные линейные нейроны. Причина в том, что градиенты, рассчитанные алгоритмом обратного распространения ошибки , имеют тенденцию уменьшаться к нулю по мере распространения активации через слои сигмоидальных нейронов, что затрудняет оптимизацию нейронных сетей, использующих несколько слоев сигмоидальных нейронов.

выпрямитель

См. также: Выпрямитель (нейронные сети)

В контексте искусственных нейронных сетей выпрямитель — или ReLU (выпрямленная линейная единица) это функция активации, определяемая как положительная часть ее аргумента:

$f(x)=x^{+}=\max(0,x),$

где x — входной сигнал нейрона. Это также известно как функция линейного изменения и аналогично полуволновому выпрямлению в электротехнике. Эта функция активации была впервые введена в динамическую сеть Ханлозером и др. в статье 2000 года в журнале Nature с сильными биологическими мотивами и математическими обоснованиями. Впервые это было продемонстрировано в 2011 году, чтобы обеспечить лучшее обучение более глубоких сетей. по сравнению с широко используемыми функциями активации до 2011 года, то есть логистической сигмоидой (которая основана на теории вероятностей ; см. логистическую регрессию ) и ее более практичной функцией. аналог — гиперболический тангенс .

Обычно используемым вариантом функции активации ReLU является Leaky ReLU, который допускает небольшой положительный градиент, когда устройство не активно:

$f(x)={\begin{cases}x&{\text{if }}x>0,\\ax&{\text{otherwise}}.\end{cases}}$

где x — входные данные нейрона, а a использовалось значение 0,01 — небольшая положительная константа (в оригинальной статье для a ).

Алгоритм псевдокода

Ниже приведена простая реализация псевдокода одного TLU, который принимает логические входные значения (истина или ложь) и возвращает один логический выход при активации. объектно -ориентированная Используется модель. Никакой метод обучения не определен, поскольку существует несколько. Если бы использовалась чисто функциональная модель, приведенный ниже класс TLU был бы заменен функциональным TLU с порогом входных параметров, весами и входными данными, которые возвращали логическое значение.

class TLU defined as:
    data member threshold : number
    data member weights : list of numbers of size X

    function member fire(inputs : list of booleans of size X) : boolean defined as:
        variable T : number
        T ← 0
        for each i in 1 to X do
            if inputs(i) is true then
                T ← T + weights(i)
            end if
        end for each
        if T > threshold then
            return true
        else:
            return false
        end if
    end function
end class

См. также

• Связывающий нейрон
• Коннекционизм

Дальнейшее чтение

• Маккалок, Уоррен С .; Питтс, Уолтер (1943). «Логическое исчисление идей, имманентных нервной деятельности». Вестник математической биофизики . 5 (4): 115–133. дои : 10.1007/bf02478259 .
• Самардак А.; Ногаре, А.; Янсон, НБ; Баланов А.Г.; Фаррер, И.; Ричи, Д.А. (5 июня 2009 г.). «Шумоконтролируемая передача сигнала в многопоточном полупроводниковом нейроне» . Письма о физических отзывах . 102 (22): 226802. Бибкод : 2009PhRvL.102v6802S . дои : 10.1103/physrevlett.102.226802 . ПМИД   19658886 . S2CID   11211062 .

Внешние ссылки

• Искусственный человека нейрон имитирует функции клеток
• Нейроны Маккалока-Питтса (обзор)