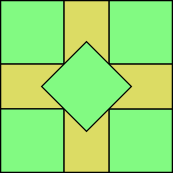
Квадратная упаковка

Квадратная упаковка — это задача упаковки , цель которой — определить, сколько конгруэнтных квадратов можно упаковать в некоторую более крупную форму, часто квадрат или круг.

Квадратная упаковка в квадрате [ править ]

Упаковка квадратов в квадрат - это задача определения максимального количества единичных квадратов (квадратов с длиной стороны один), которые можно упаковать внутри большего квадрата с длиной стороны. $a$ . Если $a$ целое число , ответ $a^{2},$ но точное – или даже асимптотическое – количество незаполненного пространства для произвольного нецелого числа $a$ это открытый вопрос. ^[1]

5 единичных квадратов в квадрате с длиной стороны

2+1/{\sqrt {2}}\approx 2.707

10 единичных квадратов в квадрате с длиной стороны

3+1/{\sqrt {2}}\approx 3.707

11 единичных квадратов в квадрате с длиной стороны

a\approx 3.877084

Наименьшее значение $a$ что позволяет упаковывать $n$ единичные квадраты известны, когда $n$ является идеальным квадратом (в этом случае это ${\sqrt {n}}$ ), а также для $n={}$ 2, 3, 5, 6, 7, 8, 10, 13, 14, 15, 24, 34, 35, 46, 47 и 48. Для большинства этих чисел (за исключением только 5 и 10) упаковка — естественная с квадратами, выровненными по осям, и $a$ является $\lceil {\sqrt {n}}\,\rceil$ , где $\lceil \,\ \rceil$ — функция потолка (округления вверх). ^[2]^[3]На рисунке показаны оптимальные упаковки для 5 и 10 квадратов — двух наименьших чисел квадратов, для которых оптимальная упаковка включает наклонные квадраты. ^[4]^[5]

Самый маленький неразрешенный случай включает упаковку 11 единичных квадратов в больший квадрат.11 единичных квадратов не могут быть упакованы в квадрат со стороной меньше $\textstyle 2+2{\sqrt {4/5}}\approx 3.789$ . Напротив, самая плотная известная упаковка из 11 квадратов находится внутри квадрата со стороной примерно 3,877084, найденного Уолтером Трампом . ^[6]^[4]

результаты Асимптотические

Нерешенная задача по математике :

Какова асимптотическая скорость роста пустого пространства при упаковке квадратов в полуцелый квадрат?

(еще нерешенные задачи по математике)

Для больших значений длины стороны $a$ , точное количество единичных квадратов, которые могут упаковать $a\times a$ площадь остается неизвестной.Всегда можно упаковать $\lfloor a\rfloor \!\times \!\lfloor a\rfloor$ сетка из выровненных по оси единичных квадратов,но при этом может остаться большая площадь, примерно $2a(a-\lfloor a\rfloor )$ , раскрытый и потраченный впустую. ^[4]Вместо этого Пол Эрдеш и Рональд Грэм показали, что при другой упаковке с помощью наклонных единичных квадратов потерянное пространство может быть значительно уменьшено до $o(a^{7/11})$ (здесь написано небольшими обозначениями o ). ^[7]Позже Грэм и Фан Чунг еще больше сократили неиспользуемое пространство до $O(a^{3/5})$ . ^[8]Однако, как Клаус Рот и Боб Вон доказали , все решения должны тратить как минимум пространство $\Omega {\bigl (}a^{1/2}(a-\lfloor a\rfloor ){\bigr )}$ . В частности, когда $a$ является полуцелым числом , потраченное впустую пространство по крайней мере пропорционально его квадратному корню . ^[9] Точная асимптотическая скорость роста потерянного пространства, даже для полуцелых длин сторон, остается открытой проблемой . ^[1]

Некоторые количества единичных квадратов никогда не являются оптимальным количеством в упаковке. В частности,если квадрат размером $a\times a$ позволяет упаковывать $n^{2}-2$ единичные квадраты, то должно быть так, что $a\geq n$ и что упаковка $n^{2}$ единичные квадраты также возможны. ^[2]

Квадратная упаковка по кругу [ править ]

Упаковка квадратов в круг — это смежная задача упаковки n единичных квадратов в круг минимально возможного радиуса. Для этой задачи известны хорошие решения для n до 35. Вот минимальные решения для n до 12: ^[10]

Количество квадратов	Радиус окружности
1	0.707...
2	1.118...
3	1.288...
4	1.414...
5	1.581...
6	1.688...
7	1.802...
8	1.978...
9	2.077...
10	2.121...
11	2.214...
12	2.236...

См. также [ править ]

Ссылки [ править ]

↑ Перейти обратно: Перейти обратно: ^а ^б Брасс, Питер; Мозер, Уильям; Пах, Янош (2005), Проблемы исследования дискретной геометрии , Нью-Йорк: Springer, стр. 45, ISBN 978-0387-23815-9 , LCCN 2005924022 , МР 2163782
↑ Перейти обратно: Перейти обратно: ^а ^б Кирни, Майкл Дж.; Шиу, Питер (2002), «Эффективная упаковка единичных квадратов в квадрат» , Электронный журнал комбинаторики , 9 (1), Research Paper 14, 14 стр., MR 1912796
^ Бенц, Вольфрам (2010), «Оптимальные упаковки квадратов из 13 и 46 единиц в квадрате» , Электронный журнал комбинаторики , 17 (R126), arXiv : 1606.03746 , doi : 10.37236/398 , MR 2729375
↑ Перейти обратно: Перейти обратно: ^а ^б ^с Фридман, Эрих (2009), «Упаковка квадратов единиц в квадратах: обзор и новые результаты» , Электронный журнал комбинаторики , Dynamic Survey 7, MR 1668055
^ Стромквист, Уолтер (2003), «Упаковка 10 или 11 единичных квадратов в квадрат» , Электронный журнал комбинаторики , 10 , Исследовательская статья 8, MR 2386538
^ Женсан, Тьерри; Рикелинк, Филипп (2005), «Улучшенная плотная упаковка конгруэнтных квадратов в квадрате», Discrete & Computational Geometry , 34 (1): 97–109, doi : 10.1007/s00454-004-1129-z , MR 2140885
^ Эрдеш, П .; Грэм, Р.Л. (1975), «Об упаковке квадратов с равными квадратами» (PDF) , Журнал комбинаторной теории , серия A, 19 : 119–123, doi : 10.1016/0097-3165(75)90099-0 , MR 0370368
^ Чанг, Фан ; Грэм, Рон (2020), «Эффективная упаковка единичных квадратов в большой квадрат» (PDF) , Discrete & Computational Geometry , 64 (3): 690–699, doi : 10.1007/s00454-019-00088-9
^ Рот, КФ ; Воган, Р.К. (1978), «Неэффективность упаковки квадратов с единичными квадратами», Журнал комбинаторной теории , серия A, 24 (2): 170–186, doi : 10.1016/0097-3165(78)90005-5 , MR 0487806
^ Фридман Эрих «Квадраты в кругах».

Внешние ссылки [ править ]

Фридман, Эрих , «Квадраты в квадратах» , Github , Центр упаковки Эриха

[Brass2005-1] Перейти обратно: Перейти обратно: ^а ^б Брасс, Питер; Мозер, Уильям; Пах, Янош (2005), Проблемы исследования дискретной геометрии , Нью-Йорк: Springer, стр. 45, ISBN 978-0387-23815-9 , LCCN 2005924022 , МР 2163782

[ks02-2] Перейти обратно: Перейти обратно: ^а ^б Кирни, Майкл Дж.; Шиу, Питер (2002), «Эффективная упаковка единичных квадратов в квадрат» , Электронный журнал комбинаторики , 9 (1), Research Paper 14, 14 стр., MR 1912796

[3] Бенц, Вольфрам (2010), «Оптимальные упаковки квадратов из 13 и 46 единиц в квадрате» , Электронный журнал комбинаторики , 17 (R126), arXiv : 1606.03746 , doi : 10.37236/398 , MR 2729375

[survey-4] Перейти обратно: Перейти обратно: ^а ^б ^с Фридман, Эрих (2009), «Упаковка квадратов единиц в квадратах: обзор и новые результаты» , Электронный журнал комбинаторики , Dynamic Survey 7, MR 1668055

[5] Стромквист, Уолтер (2003), «Упаковка 10 или 11 единичных квадратов в квадрат» , Электронный журнал комбинаторики , 10 , Исследовательская статья 8, MR 2386538

[6] Женсан, Тьерри; Рикелинк, Филипп (2005), «Улучшенная плотная упаковка конгруэнтных квадратов в квадрате», Discrete & Computational Geometry , 34 (1): 97–109, doi : 10.1007/s00454-004-1129-z , MR 2140885

[7] Эрдеш, П .; Грэм, Р.Л. (1975), «Об упаковке квадратов с равными квадратами» (PDF) , Журнал комбинаторной теории , серия A, 19 : 119–123, doi : 10.1016/0097-3165(75)90099-0 , MR 0370368

[8] Чанг, Фан ; Грэм, Рон (2020), «Эффективная упаковка единичных квадратов в большой квадрат» (PDF) , Discrete & Computational Geometry , 64 (3): 690–699, doi : 10.1007/s00454-019-00088-9

[9] Рот, КФ ; Воган, Р.К. (1978), «Неэффективность упаковки квадратов с единичными квадратами», Журнал комбинаторной теории , серия A, 24 (2): 170–186, doi : 10.1016/0097-3165(78)90005-5 , MR 0487806

[10] Фридман Эрих «Квадраты в кругах».

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

v т и Проблемы с упаковкой
Абстрактная упаковка	Бин Набор
Упаковка круга	В круге / равносторонний треугольник / равнобедренный прямоугольный треугольник / квадрат Аполлоническая прокладка Теорема об упаковке кругов Задача Таммеса (на сфере)
Сферическая упаковка	Аполлонический Конечный В сфере В кубе В цилиндре Плотная упаковка Поцелуйный номер Связанная сферическая упаковка (Хемминга)
Другая 2-D упаковка	Квадратная упаковка
Другая 3-D упаковка	Тетраэдр Эллипсоид
Пазлы	Конвей Слотаубер – Граатсма