Поворот (угол)
Было предложено Draft:Tau (математическую константу) объединить в эту статью. ( Обсудить ) Предлагается с июля 2024 г. |
| Повернуть | |
|---|---|
 против часовой стрелки Вращения вокруг центральной точки, начиная справа, где полный поворот соответствует углу поворота в 1 оборот. | |
| Общая информация | |
| Единица | Плоский угол |
| Символ | тр, пла, оборот, цикл |
| Конверсии | |
| 1 тр в... | ... равно... |
| радианы | 2 π рад ≈ 6,283 185 307 ... рад |
| миллирадианы | 2000 пи мрад ≈ 6 283 .185 307 ... мрад |
| степени | 360° |
| градиенты | 400 г |
Поворот заключенную (символ tr или pla ) — это единица плоского угла измерения , которая представляет собой угловую меру, в полный круг в его центре. Он равен 2 π радиан , 360 градусам или 400 граданам . В качестве угловой единицы один оборот также соответствует одному циклу (символ cyc или c ). [1] или на один оборот (символ rev или r ). [2] Распространенными единицами измерения частоты являются циклы в секунду (cps) и обороты в минуту (об/мин). [а] Угловая единица витка полезна, среди прочего, в связи с электромагнитными катушками (например, трансформаторами ), вращающимися объектами и количеством намоточных кривых.
В ISQ произвольное «количество оборотов» (также известное как «число оборотов» или «количество циклов») формализуется как безразмерная величина , называемая вращением , определяемая как соотношение заданного угла и полного оборота. представлен символом Н. Он .) Подразделения поворота включают полуповороты и четвертьповороты, охватывающие прямой угол и прямой угол соответственно; Также можно использовать метрические префиксы , например, сантитурны (ctr), миллитурны (mtr) и т. д.
Потому что один поворот радиан, некоторые предложили представлять с одной буквы. В 2010 году Майкл Хартл предложил использовать греческую букву. ( тау ), равный и соответствует одному обороту для большей концептуальной простоты при указании углов в радианах. [3] Первоначально это предложение не получило широкого признания в математическом сообществе. [4] но константа получила более широкое распространение, [5] был добавлен в несколько основных языков программирования и калькуляторов.
Символы единиц
[ редактировать ]Существует несколько символов единиц для хода и связанных с ним концепций.
единицы СИ
[ редактировать ]| Вращение | |
|---|---|
Другие имена | количество оборотов, количество циклов, количество оборотов, количество оборотов |
Общие символы | Н |
| И объединились | Безразмерный |
| Измерение | 1 |
В Международной системе величин (ISQ) вращение (символ N ) — это физическая величина, определяемая как количество оборотов : [6]
N — число (не обязательно целое число) оборотов, например, вращающегося тела вокруг заданной оси. Его значение определяется:
где 𝜑 обозначает меру вращательного смещения .
Приведенное выше определение является частью ISQ, формализованного в международном стандарте ISO 80000-3 (Пространство и время). [6] и принята в Международной системе единиц (СИ). [7] [8] В ISQ/SI вращение используется для получения частоты вращения ( скорости изменения вращения во времени), обозначаемой n :
Единицей частоты вращения в системе СИ является обратная секунда (с). −1 ). Распространенными единицами измерения частоты являются герцы (Гц), циклы в секунду (cps) и обороты в минуту (об/мин).
| Революция | |
|---|---|
| Единица | Вращение |
| Символ | оборот, r, цикл, c |
| Конверсии | |
| 1 оборот за... | ... равно... |
| Базовые единицы | 1 |
Замененная версия ISO 80000-3:2006 определяет «революцию» как специальное название безразмерной единицы «один». [б] который получил и другие специальные названия, например радиан. [с] Несмотря на свою размерную однородность , эти две специально названные безразмерные единицы применимы для несравнимых видов величин : поворота и угла соответственно. [10] «Цикл» также упоминается в ISO 80000-3 в определении периода . [д]
ЕС и Швейцария
[ редактировать ]Немецкий стандарт DIN 1315 (март 1974 г.) предложил для поворотов символ единицы измерения «pla» (от латинского: plenus angulus «полный угол»). [11] [12] Описанный в стандарте DIN 1301-1 (октябрь 2010 г.), так называемый Фоллвинкель («полный угол») не является единицей СИ . Однако это законная единица измерения в ЕС. [13] [14] и Швейцария. [15]
Калькуляторы
[ редактировать ]Научные калькуляторы HP 39gII и HP Prime поддерживают символ единицы «tr» для оборотов с 2011 и 2013 годов соответственно. Поддержка «tr» также была добавлена в новый RPL для HP 50g в 2016 году, а также для hp 39g+ , HP 49g+ , HP 39gs и HP 40gs в 2017 году. [16] [17] Угловой режим ПОВОРОТ был предложен для WP 43S . и [18] но калькулятор вместо этого реализует «MUL π » ( кратное π ) в качестве режима и единицы измерения с 2019 года. [19] [20]
Подразделения
[ редактировать ]Оборот можно разделить на 100 сантуритнов или 1000 миллитурнов, причем каждый миллитурн соответствует углу 0,36°, который также можно записать как 21′ 36″ . [21] [22] Транспортир , разделенный на сантитурны, обычно называется « процентным транспортиром».
Хотя процентные транспортиры существуют с 1922 года, [23] термины сантитурн, миллитурн и микрооборот были введены гораздо позже британским астрономом Фредом Хойлом в 1962 году. [21] [22] Некоторые измерительные приборы для артиллерийского и спутникового наблюдения имеют миллитурновую шкалу. [24] [25]
двоичные дроби оборота Также используются . Моряки традиционно делили поворот на 32 точки компаса , которые неявно имеют угловое расстояние 1/32 оборота. Двоичная степень , также известная как двоичный радиан (или бред ), равна 1/256 оборота . [26] Двоичная степень используется в вычислениях, чтобы угол мог быть представлен с максимально возможной точностью в одном байте . Другие меры угла, используемые в вычислениях, могут быть основаны на делении одного целого витка на 2. н равные части для других значений n . [27]
Предложения по использованию одной буквы для обозначения 2 π
[ редактировать ]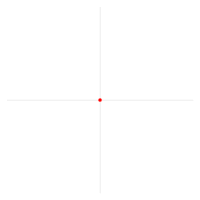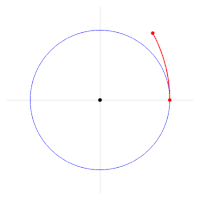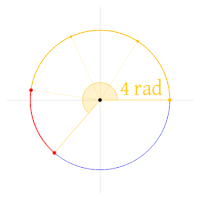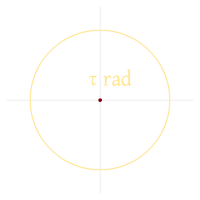

Число 2 π (приблизительно 6,28) — это отношение длины окружности к ее радиусу и количество радианов за один оборот.
Значение символа изначально не было зафиксировано соотношение длины окружности и диаметра. В 1697 году Дэвид Грегори использовал π / ρ (пи над ро) для обозначения периметра круга (т. е. окружности ), разделенного на его радиус. [28] [29] Однако ранее в 1647 году Уильям Отред использовал δ / π (дельта по числу пи) для отношения диаметра к периметру. Первое использование символа π в его нынешнем значении (периметр, разделенный на диаметр) было в 1706 году валлийским математиком Уильямом Джонсом . [30] [31]
Первое известное использование одной буквы для обозначения константы 6,28... было в Леонарда Эйлера 1727 года «Эссе, объясняющем свойства воздуха» , где она обозначалась буквой π . Эйлер позже использовал букву π для константы 3,14... в своих книгах «Механика» 1736 года и «Введение в анализ бесконечности» 1748 года , хотя и определялся как половина окружности круга радиуса 1 — единичный круг — а не как отношение длины окружности к диаметру. . В другом месте во «Introductio in analysin infinitorum» Эйлер вместо этого использовал букву π для обозначения одной четверти окружности единичного круга, или 1,57... . В конце концов, π было стандартизировано как равное 3,14..., и его использование стало широко распространенным. [32] [33]
Несколько человек независимо друг от друга предложили использовать 𝜏 = 2 π , в том числе: [34]
- Джозеф Линденбург ( ок. 1990)
- Джон Фишер (2004)
- Питер Харремоэс (2010)
- Майкл Хартл (2010)
В 2001 году Робер Пале предложил использовать число радиан за оборот в качестве фундаментальной константы круга вместо π , которое соответствует числу радиан за пол-оборота, чтобы сделать математику более простой и интуитивно понятной. В его предложении использовался символ «π с тремя ножками» для обозначения константы ( ). [35]
В 2008 году Роберт П. Криз предложил идею определения новой константы как отношения длины окружности к радиусу. Это предложение поддержал Джон Хортон Конвей . Криз использовал греческую букву пси : . [36]
В том же году Томас Колигнат предложил заглавную греческую букву тета , Θ, для обозначения 2 π . [37] Греческая буква тета происходит от финикийской и еврейской буквы тет , 𐤈 или ט, и было замечено, что старая версия символа, означающая колесо, напоминает колесо с четырьмя спицами. [38] Также было предложено использовать символ колеса, teth, для обозначения значения 2 π , а совсем недавно среди других древних культур была установлена связь с существованием символа колеса, солнца, круга или диска, то есть других вариаций. тэтов — как представление для 2 π . [39]
В 2010 году Майкл Хартл предложил использовать греческую букву тау для обозначения постоянной окружности: τ = 2 π . Он предложил несколько причин выбора константы, в первую очередь то, что она позволяет выражать доли оборота более непосредственно: например, 3 / 4 ход будет представлен как 3 τ / 4 рад вместо 3 π / 2 рад. Что касается выбора обозначений, он предложил две причины. Во-первых, τ — это количество радиан в одном обороте , причем и τ , и оборот начинаются со а / т / звука . Во-вторых, τ визуально напоминает π , ассоциация которого с константой круга неизбежна. [3] Хартла Манифест Тау [40] приводит множество примеров формул, которые, как утверждается, становятся более понятными, когда используется τ вместо π . [41] [42] [43] Например, Хартл утверждает, что замена тождества Эйлера e яπ = −1 по е это = 1 (которое Хартл также называет «тождеством Эйлера») является более фундаментальным и значимым. [40]
Первоначально ни одно из этих предложений не получило широкого признания со стороны математического и научного сообщества. [4] Однако использование τ стало более распространенным. [5] Например:
- В 2012 году образовательный сайт «Академия Хана» начал принимать ответы, выраженные через τ . [44]
- Константа τ доступна в калькуляторе Google, графическом калькуляторе Desmos. [45] и в нескольких языках программирования, таких как Python , [46] [47] Раку , [48] Обработка , [49] Nim , [50] Ржавчина , [51] GDScript , [52] Чертежи УЭ , [53] Ява , [54] [55] .СЕТЬ , [56] [57] и Один. [58]
- Он также использовался по крайней мере в одной математической исследовательской статье. [59] автор τ -промоутера Питера Харремоэса. [60]
В следующей таблице показано, как появляются различные тождества, когда используется τ = 2 π вместо π . [61] [35] Более полный список см. в разделе «Список формул, включающих π» .
| Формула | Использование π | Используя τ | Примечания |
|---|---|---|---|
| Угол, образуемый 1/4 круга | τ / 4 рад = 1/4 поворота | ||
| Окружность C круга радиуса r | |||
| Площадь круга | Площадь сектора угла θ равна A = 1 / 2 θr 2 . | ||
| Площадь правильного n- угольника с единичным радиусом описанной окружности | |||
| n -шара и n -сферы Рекуррентное соотношение объема | В 0 ( р ) знак равно 1 S 0 ( р ) знак равно 2 | ||
| Интегральная формула Коши | является границей диска, содержащего в комплексной плоскости. | ||
| Стандартное нормальное распределение | |||
| Приближение Стирлинга | |||
| n- ные корни единства | |||
| Постоянная Планка | ħ – приведенная постоянная Планка . | ||
| Угловая частота |
Преобразование единиц измерения
[ редактировать ]
Один оборот равен 2 π (≈ 6,283 185 307 179 586 ) [62] радианы , 360 градусов или 400 градусов .
| Повороты | радианы | Степени | Градианы | |
|---|---|---|---|---|
| 0 ход | 0 рад | 0° | 0 г | |
| 1/72 поворота | 𝜏 / 72 рад | π / 36 рад | 5° | 5 + 5 / 9 г |
| 1/24 поворота | 𝜏 / 24 рад | π / 12 рад | 15° | 16 + 2 / 3 г |
| 1/16 поворот | 𝜏 / 16 рад | π / 8 рад | 22.5° | 25 г |
| 1/12 поворот | 𝜏 / 12 рад | π / 6 рад | 30° | 33 + 1 / 3 г |
| 1/10 поворот | 𝜏 / 10 рад | π / 5 рад | 36° | 40 г |
| 1/8 поворота | 𝜏 / 8 рад | π / 4 рад | 45° | 50 г |
| 1 / 2 π поворот | 1 рад | в. 57,3° | в. 63,7 г | |
| 1 / 6 поворот | 𝜏 / 6 рад | π / 3 рад | 60° | 66 + 2 / 3 г |
| 1/5 поворот | 𝜏 / 5 рад | 2 π / 5 рад | 72° | 80 г |
| 1/4 поворота | 𝜏 / 4 рад | π / 2 рад | 90° | 100 г |
| 1/3 поворота | 𝜏 / 3 рад | 2 π / 3 рад | 120° | 133 + 1 / 3 г |
| 2 / 5 поворот | 2𝜏 / 5 рад | 4 π / 5 рад | 144° | 160 г |
| 1 / 2 поворот | 𝜏 / 2 рад | п рад | 180° | 200 г |
| 3 / 4 поворот | 3𝜏 / 4 рад | 3 π / 2 рад | 270° | 300 г |
| 1 ход | 𝜏 рад | 2 π рад | 360° | 400 г |
См. также
[ редактировать ]- Ампер-виток
- Герц (современный) или цикл в секунду (старый)
- Угол поворота
- Оборотов в минуту
- Повторяющийся круг
- Спат (угловая единица) — телесный угол поворота, эквивалентный 4 π стерадианам .
- Единичный интервал
- Божественные пропорции: от рациональной тригонометрии к универсальной геометрии
- Операция по модулю
- Твист (математика)
Примечания
[ редактировать ]- ^ Термины угловых единиц «циклы» и «обороты» также используются неоднозначно как более короткие версии соответствующих единиц частоты. [ нужна ссылка ]
- ^ «Специальное название «революция», символ r, для этого устройства [имя «один», символ «1»] широко используется в спецификациях вращающихся машин». [9]
- ^ «Единицами измерения величин первого измерения являются числа. В некоторых случаях этим единицам измерения даются специальные названия, например радиан...» [9]
- ^ «3-14) продолжительность периода, период: продолжительность (пункт 3‑9) одного цикла периодического события» [6]
Ссылки
[ редактировать ]- ^ Фитцпатрик, Ричард (2021). Ньютоновская динамика: Введение . ЦРК Пресс . п. 116. ИСБН 978-1-000-50953-3 . Проверено 25 апреля 2023 г.
- ^ Единицы измерения и символы для инженеров по электротехнике и электронике (PDF) . Лондон, Великобритания: Институт инженерии и технологий . 2016. Архивировано (PDF) из оригинала 18 июля 2023 г. Проверено 18 июля 2023 г. (1+iii+32+1 стр.)
- ^ Jump up to: а б Хартл, Майкл (14 марта 2019 г.) [14 марта 2010 г.]. «Манифест Тау» . Архивировано из оригинала 28 июня 2019 г. Проверено 14 сентября 2013 г.
- ^ Jump up to: а б «Жизни Пи ничего не угрожает – эксперты хладнокровно проводят кампанию по замене на тау» . Телеграф Индии . 30 июня 2011 г. Архивировано из оригинала 13 июля 2013 г. Проверено 5 августа 2019 г.
- ^ Jump up to: а б Макмиллан, Роберт (13 марта 2020 г.). «Для любителей математики ничто не может испортить День числа Пи, кроме, может быть, дня Тау» . Уолл Стрит Джорнал . ISSN 0099-9660 . Проверено 21 мая 2020 г.
- ^ Jump up to: а б с «ISO 80000-3:2019 Величины и единицы. Часть 3. Пространство и время» (2-е изд.). Международная организация по стандартизации . 2019 . Проверено 23 октября 2019 г. [1] (11 страниц)
- ^ Международная система единиц (PDF) (9-е изд.), Международное бюро мер и весов, декабрь 2022 г., ISBN 978-92-822-2272-0
- ^ Томпсон, Эмблер; Тейлор, Барри Н. (04 марта 2020 г.) [02 июля 2009 г.]. «Руководство NIST по использованию международной системы единиц, специальная публикация 811» (изд. 2008 г.). Национальный институт стандартов и технологий . Проверено 17 июля 2023 г. [2]
- ^ Jump up to: а б «ИСО 80000-3:2006» . ИСО . 2001-08-31 . Проверено 25 апреля 2023 г.
- ^ «ISO 80000-1:2009(ru) Величины и единицы. Часть 1: Общие положения» . iso.org . Проверено 12 мая 2023 г.
- ^ Герман, Зигмар; Драт, Питер (13 марта 2013 г.) [1979]. Справочник единиц СИ: Определение, внедрение, сохранение и распространение единиц СИ, основы точной измерительной техники (на немецком языке) (1-е изд.). Фридрих Vieweg & Sohn Verlagsgesellschaft mbH , перепечатка: Springer-Verlag . п. 421. ИСБН 978-3-32283606-9 . 978-3-528-08441-7, 978-3-32283606-9 . Проверено 14 августа 2015 г.
- ^ Курцвейл, Питер (09 марта 2013 г.) [1999]. Лексикон Vieweg Unit: формулы и термины из физики, химии и технологии (на немецком языке) (1-е изд.). Просмотрег, перепечатка: Springer-Verlag . п. 403. дои : 10.1007/978-3-322-92920-4 . ISBN 978-3-32292920-4 . 978-3-322-92921-1 . Проверено 14 августа 2015 г.
- ^ «Директива 80/181/EEC - Директива Совета от 20 декабря 1979 г. о сближении законов государств-членов, касающихся единиц измерения, и отменяющая Директиву 71/354/EEC» (на немецком языке). 15 февраля 1980 г. Архивировано из оригинала 22 июня 2019 г. Проверено 6 августа 2019 г.
- ^ «Директива 2009/3/EC Европейского парламента и Совета от 11 марта 2009 г., вносящая поправки в Директиву Совета 80/181/EEC о сближении законов государств-членов, касающихся единиц измерения (Текст имеет отношение к ЕЭЗ)» ( на немецком языке). 11 марта 2009 г. Архивировано из оригинала 6 августа 2019 г. Проверено 6 августа 2019 г.
- ^ «Статья 15 Единицы измерения в виде недесятичных кратных или частей единиц СИ» . Постановление о подразделении (на швейцарском верхненемецком языке). Федеральный совет Швейцарии . 23 ноября 1994 г. 941 202. Архивировано из оригинала 10 мая 2019 г. Проверено 1 января 2013 г.
- ^ Лапилли, Клаудио Даниэль (11 мая 2016 г.). «RE: newRPL: Обработка юнитов» . Музей HP . Архивировано из оригинала 10 августа 2017 г. Проверено 5 августа 2019 г.
- ^ Лапилли, Клаудио Даниэль (25 октября 2018 г.). «Глава 3: Единицы измерения – Доступные единицы измерения – Углы» . новоеРПЛ Руководство пользователя . Архивировано из оригинала 6 августа 2019 г. Проверено 7 августа 2019 г.
- ^ Пол, Матиас Р. (12 января 2016 г.) [11 января 2016 г.]. «RE: WP-32S в 2016 году?» . Музей HP . Архивировано из оригинала 5 августа 2019 г. Проверено 5 августа 2019 г.
[…] Я бы также хотел, чтобы был реализован режим ПОВОРОТ. Режим ПОВОРОТ работает точно так же, как DEG, RAD и GRAD (включая полный набор функций преобразования угловых единиц, как в WP 34S ), за исключением того, что полный круг не равен 360 градусам, 6,2831... рад или 400 гонам. но 1 ход. (Я […] обнаружил, что это действительно удобно в инженерии/программировании, где вам часто приходится конвертировать в другие представления единиц измерения или обратно […] Но я думаю, что это также может быть полезно в образовательных целях. […]) Наличие угла полного круга, нормализованного до 1, позволяет упростить преобразование в/из целого ряда других угловых единиц […]
- ^ Бонин, Уолтер (2019) [2015]. Руководство пользователя WP 43S (PDF) . 0,12 (проект ред.). стр. 72, 118–119, 311. ISBN. 978-1-72950098-9 . Архивировано (PDF) из оригинала 18 июля 2023 г. Проверено 5 августа 2019 г. [3] [4] (314 страниц)
- ^ Бонин, Уолтер (2019) [2015]. Справочное руководство WP 43S (PDF) . 0,12 (проект ред.). стр. III, 54, 97, 128, 144, 193, 195. ISBN. 978-1-72950106-1 . Архивировано (PDF) из оригинала 18 июля 2023 г. Проверено 5 августа 2019 г. [5] [6] (271 страница)
- ^ Jump up to: а б Хойл, Фред (1962). Чендлер, Миннесота (ред.). Астрономия (1-е изд.). Лондон, Великобритания: Macdonald & Co. (Publishers) Ltd. / Rathbone Books Limited. LCCN 62065943 . OCLC 7419446 . (320 страниц)
- ^ Jump up to: а б Кляйн, Герберт Артур (2012) [1988, 1974]. «Глава 8: Следя за временем» . Наука измерения: исторический обзор (Мир измерений: шедевры, загадки и путаницы метрологии) . Dover Books on Mathematics (исправленное переиздание оригинального издания). Dover Publications, Inc. / Courier Corporation (первоначально компания Simon & Schuster, Inc. ). п. 102. ИСБН 978-0-48614497-9 . LCCN 88-25858 . Проверено 6 августа 2019 г. (736 страниц)
- ^ Крокстон, Фредерик Э. (1922). «Процентный транспортир — предназначен для использования при построении круговых диаграмм или круговых диаграмм» . Журнал Американской статистической ассоциации . Короткая заметка. 18 (137): 108–109. дои : 10.1080/01621459.1922.10502455 .
- ^ Шиффнер, Фридрих (1965). Венль, Мария Эмма [на немецком языке] (ред.). «Определение орбит спутников». Астрономические сообщения обсерватории Урания в Вене (на немецком языке). 8 . Вена, Австрия: Volksbildungshaus Wiener Urania .
- ^ Хейс, Юджин Нельсон (1975) [1968]. Следопыты небес . История Смитсоновской программы спутникового слежения. Кембридж, Массачусетс, США: Academic Press / Издательство Говарда А. Дойла.
- ^ «Руководство программиста ooPIC — Глава 15: URCP» . Руководство и технические характеристики ooPIC — Компилятор ooPIC, версия 6.0 . Саваж Инновации, ООО. 2007 [1997]. Архивировано из оригинала 28 июня 2008 г. Проверено 5 августа 2019 г.
- ^ Харгривз, Шон [на польском языке] . «Углы, целые числа и арифметика по модулю» . blogs.msdn.com. Архивировано из оригинала 30 июня 2019 г. Проверено 5 августа 2019 г.
- ^ Бекманн, Петр (1989) [1970]. История Пи . Издательство Barnes & Noble .
- ^ Шварцман, Стивен (1994). Слова математики: этимологический словарь математических терминов, используемых на английском языке . Математическая ассоциация Америки . п. 165 . ISBN 978-0-88385511-9 .
- ^ Джонс, Уильям (1706). Краткое содержание Palmariorum Matheseos . Лондон: Дж. Уэйл. стр. 243 , 263 . п. 263:
Существуют различные другие способы определения длин или площадей определенных кривых линий или плоскостей , которые могут очень облегчить практику; как, например, в Круге Диаметр равен Окружности как от 1 до
Перепечатано в Смит, Дэвид Юджин (1929). «Уильям Джонс: первое использование числа π для обозначения соотношения кругов» . Справочник по математике . МакГроу-Хилл. стр. 346–347.
3.14159 и т. д. = π . Эту серию (среди других, предназначенную для той же цели и основанную на том же принципе) я получил от превосходного аналитика и моего очень уважаемого друга мистера Джона Мэчина ; и посредством него Ван Сеулена или число число, указанное в ст. 64.38. может быть проверено со всей желаемой легкостью и быстротой. - ^ Велинг, Энн (2001). «Пи сквозь века» . veling.nl . Архивировано из оригинала 2 июля 2009 г.
- ^ «Пи» . Энциклопедия Бриттаника . 14 марта 2024 г. Проверено 26 марта 2024 г.
- ^ Эйлер, Леонард (1746). Новая теория света и цвета. Брошюры различной тематики (на латыни). Амбр. Хауде и Джо. Чарльз Спенери, библиоп. п. 200.
откуда установлено, что точка В будет отведена на данное расстояние от своего естественного положения, до которого она достигнет наибольшего расстояния, по истечении прошедшего времени t=π/м, обозначающего угол π, равный 180°, который становится cos(mt)=- 1 & B b=2α.
[из чего видно, что точка B отодвинута на заданное расстояние от своего естественного положения, и максимального расстояния она достигнет по истечении прошедшего времени t=π/m, π обозначает угол 180°, который становится cos( mt)=- 1 & B b=2α.] - ^ судгилакмоэ; Хартл, Майкл (28 июня 2023 г.). Манифест Тау - С Майклом Хартлом (видео на YouTube). Информация показана в 18:35 . Проверено 24 июля 2024 г.
- ^ Jump up to: а б Пале, Робер (2001). «Пи ошибается» (PDF) . Математический интеллект . 23 (3). Нью-Йорк, США: Springer-Verlag : 7–8. дои : 10.1007/bf03026846 . S2CID 120965049 . Архивировано (PDF) из оригинала 18 июля 2019 г. Проверено 5 августа 2019 г.
- ^ Криз, Роберт (1 февраля 2008 г.). «Постоянные неудачи» . Мир физики . Институт физики . Проверено 3 августа 2024 г.
- ^ Круто, Томас «Колиньятус» (18 июля 2008 г.) [08 апреля 2008 г., 06 мая 2008 г.]. «Перенастройка тригонометрии. Новый взгляд на тригонометрию. Измерение углов в единицах измерения «метр вокруг» и использование функций единичного радиуса Xur и Yur» (PDF) . Архивировано из оригинала (PDF) 18 июля 2023 г. Проверено 18 июля 2023 г. (18 страниц)
- ^ Манн, Стив ; Янзен, Райан Э.; Али, Мир Аднан; Скурбутакос, Пит; Гулерия, Нитин (22–24 октября 2014 г.). «Интегральная кинематика (интегралы времени от расстояния, энергии и т. д.) и интегральная кинезиология» . Материалы IEEE GEM 2014 года . Торонто, Онтарио, Канада: 627–629. S2CID 6462220 . Проверено 18 июля 2023 г.
- ^ Манн, Стив ; Чен, Хунъюй; Эйлуорд, Грэм; Йорритсма, Меган; Манн, Кристина; Дефаз Поведа, Диего Давид; Пирс, Кайден; Лам, Дерек; Лестница, Джереми; Эрмандес, Джесси; Ли, Цюши; Сян, И Синь; Канаан, Жорж (июнь 2019 г.). «Глаз как камера: датчики, целостность и доверие» . 5-й семинар ACM по портативным системам и приложениям (основной доклад): 1–2. дои : 10.1145/3325424.3330210 . S2CID 189926593 . Проверено 18 июля 2023 г.
- ^ Jump up to: а б Хартл, Майкл (14 марта 2010 г.). «Манифест Тау» (PDF) . Архивировано (PDF) из оригинала 18 июля 2019 г. Проверено 5 августа 2019 г.
- ^ Арон, Джейкоб (08 января 2011 г.). «Майкл Хартл: Пришло время убить число пи». Новый учёный . Интервью. 209 (2794): 23. Бибкод : 2011NewSc.209...23A . дои : 10.1016/S0262-4079(11)60036-5 .
- ^ Ландау, Элизабет (14 марта 2011 г.). «В День Пи «пи» подвергается нападкам?» . cnn.com . CNN . Архивировано из оригинала 19 декабря 2018 г. Проверено 5 августа 2019 г.
- ^ Варфоломей, Рэндин Чарльз (25 июня 2014 г.). «Давайте использовать Тау – это проще, чем число Пи. Растущее движение утверждает, что уничтожение числа Пи сделает математику проще, легче и даже красивее» . Научный американец . Архивировано из оригинала 18 июня 2019 г. Проверено 20 марта 2015 г.
- ^ «С Днем Тау!» . blog.khanacademy.org . 28 июня 2012 г. Архивировано из оригинала 18 июля 2023 г. Проверено 19 декабря 2020 г.
- ^ «Поддерживаемые функции» . help.desmos.com . Архивировано из оригинала 26 марта 2023 г. Проверено 21 марта 2023 г.
- ^ Коглан, Ник (25 февраля 2017 г.). «PEP 628 — Добавить math.tau» . Python.org . Архивировано из оригинала 22 июля 2019 г. Проверено 5 августа 2019 г.
- ^ «математика — Математические функции» . Документация Python 3.7.0 . Архивировано из оригинала 29 июля 2019 г. Проверено 5 августа 2019 г.
- ^ «Термины Perl 6» . Архивировано из оригинала 22 июля 2019 г. Проверено 5 августа 2019 г.
- ^ «ТАУ» . Обработка . Архивировано из оригинала 22 июля 2019 г. Проверено 5 августа 2019 г.
- ^ «математика» . Ним . Архивировано из оригинала 22 июля 2019 г. Проверено 5 августа 2019 г.
- ^ "std::f64::consts::TAU — Rust" . doc.rust-lang.org . Архивировано из оригинала 18 июля 2023 г. Проверено 9 октября 2020 г.
- ^ «Константы @GDScript — документация Godot Engine (стабильная) на английском языке» . Документы Годо .
- ^ «Получить TAU — документацию Unreal Engine 5.2» . Документация по Unreal Engine .
- ^ Дарси, Джо. «JDK-8283136: Добавьте константу для тау в Math и StrictMath» . bugs.openjdk.org .
- ^ «Урок математики» . Документация Java 19 .
- ^ Джон-Гонконг. «Добавить запрос на извлечение Math.Tau № 37517 · dotnet/Runtime» . Гитхаб .
- ^ «Математика.Поле Тау» . Справочная документация по .NET .
- ^ «Математика пакета — pkg.odin-lang.org» . Документация Одина .
- ^ Харремоэс, Питер (2017). «Оценки хвостовых вероятностей для отрицательных биномиальных распределений». Кибернетика . 52 (6): 943–966. arXiv : 1601.05179 . дои : 10.14736/kyb-2016-6-0943 . S2CID 119126029 .
- ^ Харремоэс, Питер (17 ноября 2018 г.). «Постоянная Аль-Каши τ» (PDF) . Архивировано (PDF) из оригинала 22 июля 2019 г. Проверено 20 сентября 2018 г.
- ^ Эбботт, Стивен (апрель 2012 г.). «Мое обращение в тауизм» (PDF) . Математические горизонты . 19 (4): 34. doi : 10.4169/mathhorizons.19.4.34 . S2CID 126179022 . Архивировано (PDF) из оригинала 28 сентября 2013 г.
- ^ Последовательность OEIS : A019692
































