Кассини овал

Три овала Кассини, различающихся диапазоном, в который попадает параметр e (равный b / a ):

  0 < е < 1

  е = 1

  1 < е < √ 2

Не показано: e ≥ √ 2 (выпуклая).

В геометрии овал Кассини определяемая — это плоская кривая четвертого порядка, как геометрическое место точек на плоскости, такое, что произведение расстояний до двух фиксированных точек ( фокусов ) является постоянным. Это можно противопоставить эллипсу , для которого постоянна сумма расстояний, а не произведение. Овалы Кассини представляют собой частный случай полиномиальных лемнискат , когда полином используемый имеет степень 2.

Овалы Кассини названы в честь астронома Джованни Доменико Кассини, изучавшего их в конце 17 века. Кассини считал, что планета, вращающаяся вокруг другого тела, движется по одному из этих овалов, причем тело, вокруг которого она вращается, находится в одном из фокусов овала. Другие названия включают овалы Кассини , кривые Кассини и овалы Кассини .

Формальное определение

Кассини овал: $|PP_{1}|\!\!\;\times \!\!\;|PP_{2}|=b^{2}$ для любого положения P на кривой

Овал Кассини — это набор точек, такой, что для любой точки $P$ множества, произведение расстояний $|PP_{1}|,\,|PP_{2}|$ к двум фиксированным точкам $P_{1},P_{2}$ — константа, обычно записываемая как $b^{2}$ где $b>0$:

$\{P:|PP_{1}|\!\!\;\times \!\!\;|PP_{2}|=b^{2}\}\ .$

Как и в случае с эллипсом, неподвижные точки $P_{1},P_{2}$ называются фокусами овала Кассини.

Уравнения

Если фокусами являются ( a , 0) и (− a , 0), то уравнение кривой имеет вид

$((x-a)^{2}+y^{2})((x+a)^{2}+y^{2})=b^{4}.$

В расширенном виде это становится

$(x^{2}+y^{2})^{2}-2a^{2}(x^{2}-y^{2})+a^{4}=b^{4}.$

Эквивалентное полярное уравнение:

$r^{4}-2a^{2}r^{2}\cos 2\theta =b^{4}-a^{4}.\,$

Форма

Несколько овалов Кассини. ( б знак равно 0,6 а , 0,8 а , а , 1,2 а , 1,4 а , 1,6 а )

Кривая зависит с точностью до подобия от e = b / a . Когда e < 1 , кривая состоит из двух несвязных петель, каждая из которых содержит фокус. Когда e = 1 , кривая представляет собой лемнискату Бернулли, имеющую форму перевернутой восьмерки с двойной точкой (в частности, крунодой ) в начале координат. Когда e > 1 , кривая представляет собой единую связанную петлю, охватывающую оба фокуса. Он имеет форму арахиса для $1<e<{\sqrt {2}}$ и выпуклый для $e\geq {\sqrt {2}}\,.$ Предельным случаем a → 0 (следовательно, e → ∞ ), когда фокусы совпадают друг с другом, является окружность .

Кривая всегда имеет точки пересечения с x в точке ± c , где c ² = а ² + б ² . Когда e < 1, есть два дополнительных действительных точки пересечения с x , а когда e > 1 , есть два действительных точки пересечения с y , причем все остальные точки пересечения с x и y являются мнимыми.

Кривая имеет двойные точки в круговых точках на бесконечности , другими словами, кривая является бикруговой . Эти точки являются бифлекнодами, что означает, что кривая имеет две различные касательные в этих точках, и каждая ветвь кривой имеет там точку перегиба. Из этой информации и формул Плюкера можно вывести числа Плюкера для случая e ≠ 1 : степень = 4, класс = 8, количество узлов = 2, количество точек возврата = 0, количество двойных касательных = 8, количество точек перегиба = 12, рода = 1.

Касательные в круговых точках определяются как x ± iy = ± a , которые имеют действительные точки пересечения в точках (± a , 0) . Таким образом, фокусы на самом деле являются фокусами в том смысле, который определил Плюккер. Круглые точки — это точки перегиба, поэтому это тройные фокусы. Когда e ≠ 1, кривая имеет восьмой класс, что означает, что всего должно быть восемь реальных фокусов. Шесть из них были учтены в двух тройных фокусах, а остальные два находятся на уровне $${\begin{aligned}\left(\pm a{\sqrt {1-e^{4}}},0\right)&\quad (e<1),\\\left(0,\pm a{\sqrt {e^{4}-1}}\right)&\quad (e>1).\end{aligned}}$$Таким образом, дополнительные фокусы находятся на оси X , когда кривая имеет две петли, и на оси Y , когда кривая имеет одну петлю.

Овалы Кассини и ортогональные траектории

Овалы Кассини и их ортогональные траектории (гиперболы)

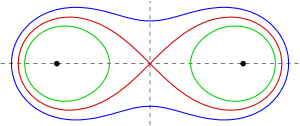
Ортогональные траектории данного пучка кривых — это кривые, ортогонально пересекающие все заданные кривые. Например, ортогональные траектории пучка софокусных эллипсов представляют собой софокусные гиперболы с теми же фокусами. Для овалов Кассини имеем:

• Ортогональные траектории кривых Кассини с фокусами $P_{1},P_{2}$ являются равносторонними гиперболами, содержащими $P_{1},P_{2}$ с тем же центром, что и овалы Кассини (см. рисунок).

Доказательство:
Для простоты выбирают $P_{1}=(1,0),\,P_{2}=(-1,0)$.

Овалы Кассини имеют уравнение $$f(x,y)=(x^{2}+y^{2})^{2}-2(x^{2}-y^{2})+1-b^{4}=0.$$

( Равносторонние гиперболы их асимптоты прямоугольные), содержащие $(1,0),(-1,0)$ с центром $(0,0)$ можно описать уравнением $$x^{2}-y^{2}-\lambda xy-1=0,\ \ \ \lambda \in \mathbb {R} .$$

Эти конические сечения не имеют y общих точек с осью и пересекают ось x в точке. $(\pm 1,0)$. Их дискриминанты показывают, что эти кривые являются гиперболами. Более детальное исследование показывает, что гиперболы имеют прямоугольную форму. Чтобы получить нормали, независимые от параметра $\lambda$ следующее неявное представление более удобно $$g(x,y)={\frac {x^{2}-y^{2}-1}{xy}}-\lambda ={\frac {x}{y}}-{\frac {y}{x}}-{\frac {1}{xy}}-\lambda =0\;.$$Простой расчет показывает, что $\operatorname {grad} f(x,y)\cdot \operatorname {grad} g(x,y)=0$ для всех $(x,y),\,x\neq 0\neq y$. Следовательно, овалы Кассини и гиперболы пересекаются ортогонально.

Примечание:
Изображение, изображающее овалы Кассини и гиперболы, выглядит как эквипотенциальные кривые двух равных точечных зарядов вместе с линиями генерируемого электрического поля . Но для потенциала двух равных точечных зарядов имеем $1/|PP_{1}|+1/|PP_{2}|={\text{constant}}$. (См. Неявная кривая .) Вместо этого эти кривые фактически соответствуют (плоским сечениям) эквипотенциальным множествам двух бесконечных проводов с одинаковой постоянной линейной плотностью заряда или, альтернативно, множествам уровня сумм функций Грина для лапласиана в двух размеры с центром в фокусах.

Однопетлевые и двухпетлевые кривые Кассини можно представить как ортогональные друг другу траектории, когда каждое семейство является коаксиальным, но не конфокальным. Если одноциклы описываются формулой $(x^{2}+y^{2})-1=axy$ тогда фокусы переменны на оси $y=x$ если $a>0$, $y=-x$ если $a<0$; если двойные петли описываются формулой $(x^{2}+y^{2})+1=b(x^{2}-y^{2})$ тогда оси соответственно $y=0$ и $x=0$. Каждая кривая с точностью до подобия дважды появляется на изображении, которое теперь напоминает силовые линии и потенциальные кривые для четырех равных точечных зарядов, расположенных $(\pm 1,0)$ и $(0,\pm 1)$. Далее, часть этого изображения в верхней полуплоскости изображает следующую ситуацию: двойные петли представляют собой сокращенный набор классов конгруэнтности для центральных коник Штейнера в гиперболической плоскости, полученных прямыми коллинеациями; и каждая одиночная петля является геометрическим местом точек $P$ такой, что угол $OPQ$ постоянна, где $O=(0,1)$ и $Q$ является основанием перпендикуляра, проходящего через $P$ на линии, описанной $x^{2}+y^{2}=1$.

Примеры

Вторая лемниската множества Мандельброта представляет собой овал Кассини, определяемый уравнением $L_{2}=\{c:\operatorname {abs} (c^{2}+c)=ER\}.$ Его фокусы находятся в точках c на комплексной плоскости , орбиты которых имеют каждое второе значение z равно нулю, что соответствует значениям 0 и −1.

Овалы Кассини - это квадрат

Овалы Кассини как плоские сечения тора (тор справа представляет собой тор веретена )

Овалы Кассини выглядят как плоские сечения торов , но только тогда, когда секущая плоскость параллельна оси тора и ее расстояние до оси равно радиусу образующей окружности (см. Рисунок).

Пересечение тора с уравнением

$\left(x^{2}+y^{2}+z^{2}+R^{2}-r^{2}\right)^{2}=4R^{2}\!\left(x^{2}+y^{2}\right)$

и самолет $y=r$ урожайность

$\left(x^{2}+z^{2}+R^{2}\right)^{2}=4R^{2}\!\left(x^{2}+r^{2}\right).$

Частично разрешив первую скобку, получим уравнение

$\left(x^{2}+z^{2}\right)^{2}-2R^{2}(x^{2}-z^{2})=4R^{2}r^{2}-R^{4},$

которое представляет собой уравнение овала Кассини с параметрами $b^{2}=2Rr$ и $a=R$.

Обобщения

Метод Кассини легко обобщить на кривые и поверхности с произвольным количеством определяющих точек:

• $|PP_{1}|\times |PP_{2}|\times \cdots \times |PP_{n}|=b^{n}$

описывает в плоском случае неявную кривую , а в трехмерном пространстве - неявную поверхность .

• 
  кривая с 3 определяющими точками
• 
  поверхность с 6 определяющими точками

См. также

• Двухцентровые биполярные координаты

Ссылки

Библиография

• Ж.-Д. Кассини (1693 г.). О происхождении и развитии астрономии и ее использовании в географии и мореплавании . Королевская типография. стр. 36 .
• Коэн, И. Бернард (1962). «Лейбниц на эллиптических орбитах: как видно из его переписки с Королевской академией наук в 1700 году». Журнал истории медицины и смежных наук . 17 (1): 72–82. дои : 10.1093/jhmas/xvii.1.72 . JSTOR   24620858 .
• Дж. Деннис Лоуренс (1972). Каталог специальных плоских кривых . Дуврские публикации . стр. 5, 153–155 . ISBN  0-486-60288-5 .
• А. Б. Бассет (1901). Элементарный трактат о кубических кривых и кривых четвертой степени . Лондон: Deighton Bell and Co., стр. 162 и далее.
• Лоуден, Д.Ф., «Семейства овалов и их ортогональные траектории», Mathematical Gazette 83, ноябрь 1999 г., 410–420.

Внешние ссылки

• «Овал Кассини» . Энциклопедия математики . ЭМС Пресс . 2001 [1994].
• Описание MacTutor
• Вайсштейн, Эрик В. «Овалы Кассини» . Математический мир .
• Описание сайта 2Dcurves.com
• «MacTutor История математики» Знаменитые кривые