Методы вычисления квадратных корней

Методы вычисления квадратных корней - это алгоритмы аппроксимации неотрицательного квадратного корня. ${\sqrt {S}}$ положительного действительного числа $S$. Поскольку все квадратные корни из натуральных чисел , кроме полных квадратов , иррациональны , Квадратные корни обычно можно вычислить только с некоторой конечной точностью: эти методы обычно создают серию все более точных приближений .

Большинство методов вычисления квадратного корня являются итеративными: после выбора подходящей начальной оценки ${\sqrt {S}}$, итеративное уточнение выполняется до тех пор, пока не будет выполнен некоторый критерий завершения. Одной из схем уточнения является метод Герона , частный случай метода Ньютона . Если деление обходится гораздо дороже, чем умножение, вместо этого может быть предпочтительнее вычислить обратный квадратный корень .

Другие методы доступны для вычисления квадратного корня по цифрам или с использованием ряда Тейлора . Рациональные аппроксимации квадратных корней можно вычислить с помощью разложения цепных дробей .

Используемый метод зависит от необходимой точности, а также доступных инструментов и вычислительной мощности. Эти методы можно грубо классифицировать как методы, подходящие для вычислений в уме, методы, обычно требующие, по крайней мере, бумаги и карандаша, и методы, которые реализованы в виде программ, выполняемых на цифровом электронном компьютере или другом вычислительном устройстве. Алгоритмы могут учитывать сходимость (сколько итераций требуется для достижения заданной точности), вычислительную сложность отдельных операций (т. е. деления) или итераций, а также распространение ошибок (точность конечного результата).

Некоторые методы, такие как синтетическое деление бумаги и карандаша и расширение серии, не требуют начального значения. В некоторых приложениях целочисленный квадратный корень требуется , который представляет собой квадратный корень, округленный или усеченный до ближайшего целого числа (в этом случае может использоваться модифицированная процедура).

История

Процедуры поиска квадратных корней (особенно квадратного корня из 2 ) известны, по крайней мере, со времен древнего Вавилона в 17 веке до нашей эры. Вавилонские математики вычислили квадратный корень из 2–3 шестидесятеричных «цифр» после 1, но неизвестно, как именно. Они знали, как определить гипотенузу, используя

$${\sqrt {a^{2}+b^{2}}}\approx a+{\frac {1}{2}}b^{2}a^{-1}$$

(приведя для примера ${\frac {41}{60}}+{\frac {15}{3600}}$ для диагонали ворот, высота которой равна ${\frac {40}{60}}$ стержни и ширина которых ${\frac {10}{60}}$ стержни), и они, возможно, использовали аналогичный подход для нахождения аппроксимации ${\sqrt {2}}.$

Метод Герона из Египта первого века был первым установленным алгоритмом вычисления квадратного корня.

Современные аналитические методы начали развиваться после введения арабской системы счисления в Западную Европу в эпоху раннего Возрождения.

Сегодня почти все вычислительные устройства имеют быструю и точную функцию извлечения квадратного корня либо в виде конструкции языка программирования, встроенной функции компилятора или библиотеки, либо в качестве аппаратного оператора, основанного на одной из описанных процедур.

оценка

Многие итеративные алгоритмы квадратного корня требуют начального начального значения . Начальное число должно быть ненулевым положительным числом; оно должно быть между 1 и $S$, число, квадратный корень которого требуется, поскольку квадратный корень должен находиться в этом диапазоне. Если начальное число находится далеко от корня, алгоритму потребуется больше итераций. Если кто-то инициализируется с $x_{0}=1$ (или $S$), то примерно ${\tfrac {1}{2}}\vert \log _{2}S\vert$ итерации будут потрачены впустую, просто чтобы получить порядок величины корня. Поэтому полезно иметь приблизительную оценку, которая может иметь ограниченную точность, но ее легко вычислить. В общем, чем лучше первоначальная оценка, тем быстрее сходимость. Для метода Ньютона (также называемого вавилонским методом или методом Герона) семя, несколько большее, чем корень, сходится немного быстрее, чем семя, несколько меньшее, чем корень.

В общем, оценка соответствует произвольному интервалу, который, как известно, содержит корень (например, $[x_{0},S/x_{0}]$). Оценка представляет собой конкретное значение функциональной аппроксимации $f(x)={\sqrt {x}}$ за интервал. Получение лучшей оценки предполагает либо получение более точных границ интервала, либо поиск лучшего функционального приближения к $f(x)$. Последнее обычно означает использование в приближении полинома более высокого порядка, хотя не все приближения являются полиномиальными. Общие методы оценки включают скалярный, линейный, гиперболический и логарифмический. Десятичная система счисления обычно используется для оценок в уме или на бумаге. Двоичная база больше подходит для компьютерных оценок. При оценке показатель степени и мантисса обычно рассматриваются отдельно, поскольку число выражается в научной форме.

Десятичные оценки

Обычно число $S$ выражается в научной записи как $a\times 10^{2n}$ где $1\leq a<100$ и n представляет собой целое число, а диапазон возможных квадратных корней равен ${\sqrt {a}}\times 10^{n}$ где $1\leq {\sqrt {a}}<10$.

оценки

Скалярные методы делят диапазон на интервалы, и оценка в каждом интервале представлена ​​одним скалярным числом. Если диапазон рассматривать как один интервал, среднее арифметическое (5,5) или среднее геометрическое ( ${\sqrt {10}}\approx 3.16$) раз $10^{n}$ являются правдоподобными оценками. Абсолютная и относительная погрешность для них будут различаться. В общем, один скаляр будет очень неточным. Лучшие оценки делят диапазон на два или более интервала, но скалярные оценки по своей сути имеют низкую точность.

Для двух интервалов, разделенных геометрически, квадратный корень ${\sqrt {S}}={\sqrt {a}}\times 10^{n}$ можно оценить как

$${\sqrt {S}}\approx {\begin{cases}2\cdot 10^{n}&{\text{if }}a<10,\\6\cdot 10^{n}&{\text{if }}a\geq 10.\end{cases}}$$

Эта оценка имеет максимальную абсолютную ошибку $4\cdot 10^{n}$ при a = 100 и максимальная относительная ошибка 100% при a = 1.

Например, для $S=125348$ факторизованный как $12.5348\times 10^{4}$, оценка ${\sqrt {S}}\approx 6\cdot 10^{2}=600$. ${\sqrt {125348}}=354.0$, абсолютная ошибка 246 и относительная ошибка почти 70%.

оценки

Лучшей оценкой и используемым стандартным методом является линейное приближение функции $y=x^{2}$ по небольшой дуге. Если, как указано выше, степени основания вычтены из числа $S$ и интервал сократился до $[1,100]$В качестве аппроксимации можно использовать секущую линию, охватывающую дугу, или касательную линию где-то вдоль дуги, но линия регрессии наименьших квадратов, пересекающая дугу, будет более точной.

Линия регрессии по методу наименьших квадратов минимизирует среднюю разницу между оценкой и значением функции. Его уравнение $y=8.7x-10$. Изменение порядка, $x=0.115y+1.15$. Округляя коэффициенты для удобства вычислений,

$${\sqrt {S}}\approx (a/10+1.2)\cdot 10^{n}$$

это лучшая оценка В среднем , которую можно получить с помощью единичной линейной аппроксимации функции y=x. ² в интервале $[1,100]$. Он имеет максимальную абсолютную ошибку 1,2 при a=100 и максимальную относительную ошибку 30% при S=1 и 10.

Чтобы разделить на 10, вычтите единицу из показателя степени. $a$, или образно переместите десятичную запятую на одну цифру влево. Для этой формулировки любая аддитивная константа 1 плюс небольшое приращение даст удовлетворительную оценку, поэтому запоминание точного числа не является обузой. Аппроксимация (округленная или нет) с использованием одной линии, охватывающей диапазон. $[1,100]$ точность меньше одной значащей цифры; относительная ошибка больше 1/2 ² , поэтому предоставляется менее 2 бит информации. Точность сильно ограничена, поскольку диапазон составляет два порядка, что довольно велико для такого рода оценок.

Гораздо лучшую оценку можно получить с помощью кусочно-линейной аппроксимации: нескольких отрезков прямой, каждый из которых аппроксимирует некоторую поддугу оригинала. Чем больше сегментов линий используется, тем лучше аппроксимация. Самый распространенный способ — использовать касательные линии; Важнейшим выбором является то, как разделить дугу и где разместить точки касания. Эффективный способ разделить дугу от y = 1 до y = 100 — геометрический: для двух интервалов границы интервалов представляют собой квадратный корень из границ исходного интервала, 1 × 100, т. е. [1, ² √ 100 ] и [ ² √ 100,100 ]. Для трех интервалов границами являются кубические корни из 100: [1, ³ √ 100 ], [ ³ √ 100 ,( ³ √ 100 ) ² ], и [( ³ √ 100 ) ² ,100] и т. д. Для двух интервалов ² √ 100 = 10, очень удобное число. Касательные линии легко вывести, они расположены в точках x = √ 1* √ 10 и x = √ 10* √ 10 . Их уравнения: $y=3.56x-3.16$ и $y=11.2x-31.6$. При инвертировании квадратные корни равны: $x=0.28y+0.89$ и $x=.089y+2.8$. Таким образом, для $S=a\cdot 10^{2n}$:

$${\sqrt {S}}\approx {\begin{cases}(0.28a+0.89)\cdot 10^{n}&{\text{if }}a<10,\\(.089a+2.8)\cdot 10^{n}&{\text{if }}a\geq 10.\end{cases}}$$

Максимальные абсолютные ошибки наблюдаются в верхних точках интервалов при а =10 и 100 и составляют 0,54 и 1,7 соответственно. Максимальные относительные ошибки приходятся на концы интервалов, при а =1, 10 и 100, и составляют в обоих случаях 17%. 17% или 0,17 больше, чем 1/10, поэтому метод дает точность менее десятичной цифры.

оценки

В некоторых случаях гиперболические оценки могут быть эффективными, поскольку гипербола также является выпуклой кривой и может лежать вдоль дуги Y = x. ² лучше, чем линия. Гиперболические оценки более сложны в вычислительном отношении, поскольку они обязательно требуют плавающего деления. Почти оптимальное гиперболическое приближение к x ² на интервале $[1,100]$ составляет у=190/(10-х)-20. При транспонировании квадратный корень равен x = -190/(y+20)+10. Таким образом, для $S=a\cdot 10^{2n}$:

$${\sqrt {S}}\approx \left({\frac {-190}{a+20}}+10\right)\cdot 10^{n}$$

Плавающее деление должно иметь точность только до одной десятичной цифры, потому что общая оценка является настолько точной и может быть сделана в уме. Гиперболическая оценка в среднем лучше, чем скалярная или линейная оценка. Максимальная абсолютная ошибка составляет 1,58 при 100 и максимальная относительная ошибка 16,0% при 10. Для худшего случая при a = 10 оценка составляет 3,67. Если начать с 10 и сразу применить итерации Ньютона-Рафсона, потребуются две итерации, что даст 3,66, прежде чем точность гиперболической оценки будет превышена. Для более типичного случая, такого как 75, гиперболическая оценка равна 8,00, и для получения более точного результата потребуется 5 итераций Ньютона-Рафсона, начиная с 75.

оценки

Метод, аналогичный кусочно-линейной аппроксимации, но использующий только арифметику вместо алгебраических уравнений, использует таблицу умножения наоборот: квадратный корень числа от 1 до 100 находится между 1 и 10, поэтому, если мы знаем, что 25 - это идеальный квадрат (5 × 5), а 36 — полный квадрат (6 × 6), то квадратный корень из числа, большего или равного 25, но меньше 36, начинается с цифры 5. Аналогично для чисел между другими квадратами. Этот метод даст правильную первую цифру, но он не имеет точности до одной цифры: например, первая цифра квадратного корня из 35 равна 5, но квадратный корень из 35 равен почти 6.

Лучший способ — разделить диапазон на интервалы посередине между квадратами. Итак, любое число между 25 и половиной пути к 36, что равно 30,5, оценивается как 5; любое число от 30,5 до 36, оценка 6. Процедура требует лишь небольшой арифметики, чтобы найти граничное число в середине двух произведений таблицы умножения. Вот справочная таблица этих границ:

а	ближайшая площадь	$k={\sqrt {a}}$ Восток.
от 1 до 2,5	1 (= 1 2 )	1
от 2,5 до 6,5	4 (= 2 2 )	2
от 6,5 до 12,5	9 (= 3 2 )	3
от 12,5 до 20,5	16 (= 4 2 )	4
от 20,5 до 30,5	25 (= 5 2 )	5
от 30,5 до 42,5	36 (= 6 2 )	6
от 42,5 до 56,5	49 (= 7 2 )	7
от 56,5 до 72,5	64 (= 8 2 )	8
от 72,5 до 90,5	81 (= 9 2 )	9
от 90,5 до 100	100 (= 10 2 )	10

Последняя операция — умножить оценку k на степень десяти, разделенную на 2, так что для $S=a\cdot 10^{2n}$,

$${\sqrt {S}}\approx k\cdot 10^{n}$$

Этот метод неявно дает одну значащую цифру точности, поскольку он округляется до лучшей первой цифры.

В большинстве случаев метод можно расширить на 3 значащие цифры путем интерполяции между ближайшими квадратами, ограничивающими операнд. Если $k^{2}\leq a<(k+1)^{2}$, затем ${\sqrt {a}}$ примерно k плюс дробь, разница между a и k ² делится на разницу между двумя квадратами:

$${\sqrt {a}}\approx k+R$$

где

$$R={\frac {(a-k^{2})}{(k+1)^{2}-k^{2}}}$$

Последняя операция, как указано выше, заключается в умножении результата на степень десяти, разделенную на 2;

$${\sqrt {S}}={\sqrt {a}}\cdot 10^{n}\approx (k+R)\cdot 10^{n}$$

k — десятичная цифра, а R — дробь, которую необходимо преобразовать в десятичную. Обычно он имеет только одну цифру в числителе и одну или две цифры в знаменателе, поэтому преобразование в десятичную дробь можно выполнить мысленно.

Пример: найти квадратный корень из 75. 75 = 75 × 10. ^{2  · 0} , поэтому a равно 75, а n равно 0. Из таблицы умножения квадратный корень из мантиссы должен быть равен 8 точкам , потому что 8 × 8 — это 64, а 9 × 9 — это 81, это слишком много, поэтому k равно 8; что-то это десятичное представление R. — Дробь R равна 75 - k ² = 11, числитель, и 81 - k ² = 17, знаменатель. 11/17 — это немного меньше, чем 12/18, что составляет 2/3 секунды или 0,67, поэтому угадайте 0,66 (здесь можно угадать, ошибка очень маленькая). Таким образом, оценка равна 8 + 0,66 = 8,66 . √ 75 до трех значащих цифр равно 8,66, поэтому оценка верна до трех значащих цифр. Не все такие оценки с использованием этого метода будут столь точными, но они будут близки.

оценки

При работе в двоичной системе счисления (как это делают компьютеры внутри себя), выражая $S$ как $a\times 2^{2n}$ где $0.1_{2}\leq a<10_{2}$, квадратный корень ${\sqrt {S}}={\sqrt {a}}\times 2^{n}$ можно оценить как

$${\sqrt {S}}\approx (0.485+0.485\cdot a)\cdot 2^{n}$$

что представляет собой линию регрессии метода наименьших квадратов к коэффициентам из трех значащих цифр. ${\sqrt {a}}$ имеет максимальную абсолютную ошибку 0,0408 при $a$=2, и максимальная относительная ошибка 3,0% при $a$=1. Удобная в вычислительном отношении округленная оценка (поскольку коэффициенты представляют собой степени 2):

${\sqrt {S}}\approx (0.5+0.5\cdot a)\cdot 2^{n}$

который имеет максимальную абсолютную ошибку 0,086 при 2 и максимальную относительную ошибку 6,1% при a = 0,5 и a = 2,0 .

Для $S=125348=1\;1110\;1001\;1010\;0100_{2}=1.1110\;1001\;1010\;0100_{2}\times 2^{16}\,$, бинарное приближение дает ${\sqrt {S}}\approx (0.5+0.5\cdot a)\cdot 2^{8}=1.0111\;0100\;1101\;0010_{2}\cdot 1\;0000\;0000_{2}=1.456\cdot 256=372.8$. ${\sqrt {125348}}=354.0$, поэтому оценка имеет абсолютную ошибку 19 и относительную ошибку 5,3%. Относительная погрешность чуть меньше 1/2. ⁴ , поэтому оценка хороша для 4+ бит.

Оценка для $a$ хорошие до 8 бит можно получить путем поиска в таблице по старшим 8 битам $a$, помня, что старший бит неявно присутствует в большинстве представлений с плавающей запятой, а нижний бит числа 8 должен быть округлен. Таблица представляет собой 256 байт предварительно вычисленных 8-битных значений квадратных корней. Например, для индекса 11101101 _2, представляющего 1,8515625 ₁₀ , запись имеет вид 10101110 _2, представляющего 1,359375 ₁₀ , квадратный корень из 1,8515625 ₁₀ с точностью до 8 бит (2+ десятичные цифры).

Метод Герона

«Метод Герона» перенаправляется сюда. Формулу, используемую для нахождения площади треугольника, см. в формуле Герона .

Первый явный алгоритм аппроксимации $\ {\sqrt {S~}}\$ известен как метод Герона , в честь греческого математика первого века Героя Александрийского , который описал этот метод в своей 60 года нашей эры работе «Метрика» . Этот метод еще называют вавилонским методом (не путать с вавилонским методом приближения гипотенуз ), хотя нет никаких свидетельств того, что этот метод был известен вавилонянам.

Учитывая положительное действительное число $S$, пусть x ₀ > 0 — любая положительная начальная оценка . Метод Герона заключается в итеративном вычислении

$$x_{n+1}={\frac {1}{2}}\left(x_{n}+{\frac {S}{x_{n}}}\right),$$

пока не будет достигнута желаемая точность. Последовательность $\ {\bigl (}\ x_{0},\ x_{1},\ x_{2},\ x_{3},\ \ldots \ {\bigr )}\$ определяемое этим уравнением, сходится к $\ \lim _{n\to \infty }x_{n}={\sqrt {S~}}~.$

Это эквивалентно использованию метода Ньютона для решения $x^{2}-S=0$. Этот алгоритм является квадратично сходящимся : количество правильных цифр числа $x_{n}$ примерно удваивается с каждой итерацией.

Вывод

Основная идея заключается в том, что если $\ x\$ является завышенной оценкой квадратного корня из неотрицательного действительного числа $\ S\$ затем $\ {\tfrac {\ S\ }{x}}\$ будет заниженной, и наоборот, поэтому можно разумно ожидать, что среднее этих двух чисел обеспечит лучшее приближение (хотя формальное доказательство этого утверждения зависит от неравенства средних арифметических и геометрических, которое показывает, что это среднее всегда является завышенной оценкой). квадратного корня, как отмечено в статье о квадратных корнях , что обеспечивает сходимость).

Точнее, если $\ x\$ это наше первоначальное предположение $\ {\sqrt {S~}}\$ и $\ \varepsilon \$ – ошибка в нашей оценке такая, что $\ S=\left(x+\varepsilon \right)^{2}\ ,$ тогда мы можем разложить бином как:

$$\ {\bigl (}\ x+\varepsilon \ {\bigr )}^{2}=x^{2}+2x\varepsilon +\varepsilon ^{2}$$

и найдите член ошибки

$\varepsilon ={\frac {\ S-x^{2}\ }{\ 2x+\varepsilon \ }}\approx {\frac {\ S-x^{2}\ }{2x}}\ ,$ если мы предположим, что $\ \varepsilon \ll x~$

Следовательно, мы можем компенсировать ошибку и обновить нашу старую оценку как

$$\ x+\varepsilon \ \approx \ x+{\frac {\ S-x^{2}\ }{2x}}\ =\ {\frac {\ S+x^{2}\ }{2x}}\ =\ {\frac {\ {\frac {S}{\ x\ }}+x\ }{2}}\ \equiv \ x_{\mathsf {revised}}~.$$

Поскольку вычисленная ошибка не была точной, это не фактический ответ, а наше новое предположение, которое мы будем использовать в следующем раунде коррекции. Процесс обновления повторяется до тех пор, пока не будет получена желаемая точность.

Этот алгоритм одинаково хорошо работает с p -адическими числами , но его нельзя использовать для идентификации действительных квадратных корней с p -адическими квадратными корнями; с помощью этого метода можно, например, построить последовательность рациональных чисел, которая сходится к +3 в действительных числах и к -3 в 2-адических числах.

Пример

Чтобы рассчитать $\ {\sqrt {S~}}\$ для $\ S=125348\ ,$ до шести значащих цифр, используйте приведенный выше метод грубой оценки, чтобы получить

$${\begin{aligned}{\begin{array}{rlll}x_{0}&=6\cdot 10^{2}&&=600.000\\[0.3em]x_{1}&={\frac {\ 1\ }{2}}\left(x_{0}+{\frac {S}{\;x_{0}\ }}\right)&={\frac {\ 1\ }{2}}\left(600.000+{\frac {\ 125348\ }{600.000}}\right)&=404.457\\[0.3em]x_{2}&={\frac {\ 1\ }{2}}\left(x_{1}+{\frac {S}{\;x_{1}\ }}\right)&={\frac {\ 1\ }{2}}\left(404.457+{\frac {\ 125348\ }{404.457}}\right)&=357.187\\[0.3em]x_{3}&={\frac {\ 1\ }{2}}\left(x_{2}+{\frac {S}{\;x_{2}\ }}\right)&={\frac {\ 1\ }{2}}\left(357.187+{\frac {\ 125348\ }{357.187}}\right)&=354.059\\[0.3em]x_{4}&={\frac {\ 1\ }{2}}\left(x_{3}+{\frac {S}{\;x_{3}\ }}\right)&={\frac {\ 1\ }{2}}\left(354.059+{\frac {\ 125348\ }{354.059}}\right)&=354.045\\[0.3em]x_{5}&={\frac {\ 1\ }{2}}\left(x_{4}+{\frac {S}{\;x_{4}\ }}\right)&={\frac {\ 1\ }{2}}\left(354.045+{\frac {\ 125348\ }{354.045}}\right)&=354.045\ \end{array}}\end{aligned}}$$

Поэтому $\ {\sqrt {125348~}}\approx 354.045\$ до трех десятичных знаков.

Конвергенция

Полулогарифмические графики, сравнивающие скорость сходимости метода Герона для нахождения квадратного корня из 100 для различных начальных предположений. Отрицательные предположения сходятся к отрицательному корню, положительные — к положительному корню. Обратите внимание, что значения ближе к корню сходятся быстрее, и все приближения являются завышенными. В файле SVG наведите указатель мыши на график, чтобы отобразить его точки.

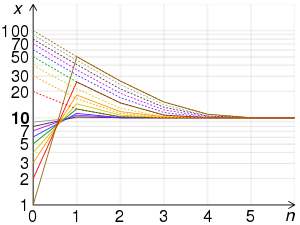
Предположим, что $\ x_{0}>0~~{\mathsf {and}}~~S>0~.$ Тогда для любого натурального числа $\ n:x_{n}>0~.$ Пусть погрешность относительная $\ x_{n}\$ определяться

$$\ \varepsilon _{n}={\frac {~x_{n}\ }{\ {\sqrt {S~}}\ }}-1>-1\$$

и таким образом

$$\ x_{n}={\sqrt {S~}}\cdot \left(1+\varepsilon _{n}\right)~.$$

Тогда можно показать, что

$$\ \varepsilon _{n+1}={\frac {\varepsilon _{n}^{2}}{2(1+\varepsilon _{n})}}\geq 0~.$$

И таким образом, что

$$\ \varepsilon _{n+2}\leq \min \left\{\ {\frac {\ \varepsilon _{n+1}^{2}\ }{2}},{\frac {\ \varepsilon _{n+1}\ }{2}}\ \right\}\$$

и, следовательно, сходимость обеспечена и является квадратичной .

Худший случай конвергенции

Если использовать приведенную выше приблизительную оценку с вавилонским методом, то наименее точные случаи в порядке возрастания будут следующими:

$${\begin{aligned}S&=\ 1\ ;&x_{0}&=\ 2\ ;&x_{1}&=\ 1.250\ ;&\varepsilon _{1}&=\ 0.250~.\\S&=\ 10\ ;&x_{0}&=\ 2\ ;&x_{1}&=\ 3.500\ ;&\varepsilon _{1}&<\ 0.107~.\\S&=\ 10\ ;&x_{0}&=\ 6\ ;&x_{1}&=\ 3.833\ ;&\varepsilon _{1}&<\ 0.213~.\\S&=\ 100\ ;&x_{0}&=\ 6\ ;&x_{1}&=\ 11.333\ ;&\varepsilon _{1}&<\ 0.134~.\end{aligned}}$$

Таким образом, в любом случае

$${\begin{aligned}\varepsilon _{1}&\leq 2^{-2}.\\\varepsilon _{2}&<2^{-5}<10^{-1}~.\\\varepsilon _{3}&<2^{-11}<10^{-3}~.\\\varepsilon _{4}&<2^{-23}<10^{-6}~.\\\varepsilon _{5}&<2^{-47}<10^{-14}~.\\\varepsilon _{6}&<2^{-95}<10^{-28}~.\\\varepsilon _{7}&<2^{-191}<10^{-57}~.\\\varepsilon _{8}&<2^{-383}<10^{-115}~.\end{aligned}}$$

Ошибки округления замедляют сходимость. Рекомендуется оставить хотя бы одну дополнительную цифру сверх желаемой точности. $\ x_{n}\$ рассчитывается, чтобы избежать значительной ошибки округления.

Метод Бахшали

Этот метод нахождения приближения к квадратному корню был описан в древнеиндийском манускрипте , называемом манускриптом Бахшали . Это эквивалентно двум итерациям вавилонского метода, с x0 _{начиная} . Таким образом, алгоритм является четвертично сходящимся, а это означает, что количество правильных цифр аппроксимации увеличивается примерно в четыре раза с каждой итерацией. Исходное представление в современных обозначениях выглядит следующим образом: Чтобы вычислить ${\sqrt {S}}$, позволять $x_{0}^{2}$ быть начальным приближением к $S$. Затем последовательно выполните итерацию как:

$${\begin{aligned}a_{n}&={\frac {S-x_{n}^{2}}{2x_{n}}},\\b_{n}&=x_{n}+a_{n},\\x_{n+1}&=b_{n}-{\frac {a_{n}^{2}}{2b_{n}}}=(x_{n}+a_{n})-{\frac {a_{n}^{2}}{2(x_{n}+a_{n})}}.\end{aligned}}$$

Это можно использовать для построения рационального приближения к квадратному корню, начиная с целого числа. Если $x_{0}=N$ целое число, выбранное так $N^{2}$ близко к $S$, и $d=S-N^{2}$ – это разница, абсолютное значение которой минимизировано, то первую итерацию можно записать как:

$${\sqrt {S}}\approx N+{\frac {d}{2N}}-{\frac {d^{2}}{8N^{3}+4Nd}}={\frac {8N^{4}+8N^{2}d+d^{2}}{8N^{3}+4Nd}}={\frac {N^{4}+6N^{2}S+S^{2}}{4N^{3}+4NS}}={\frac {N^{2}(N^{2}+6S)+S^{2}}{4N(N^{2}+S)}}.$$

Метод Бахшали можно обобщить на вычисление произвольного корня, в том числе дробных.

Пример

Используя тот же пример, что и для вавилонского метода, пусть $S=125348.$ Тогда первая итерация дает

$${\begin{aligned}x_{0}&=600\\[1ex]a_{1}&={\frac {125348-600^{2}}{2\times 600}}&&=&-195.543\\[1ex]b_{1}&=600+(-195.543)&&=&404.456\\[1ex]x_{1}&=404.456-{\frac {(-195.543)^{2}}{2\times 404.456}}&&=&357.186\end{aligned}}$$

Аналогично вторая итерация дает

$${\begin{aligned}a_{2}&={\frac {125348-357.186^{2}}{2\times 357.186}}&&=&-3.126\\[1ex]b_{2}&=357.186+(-3.126)&&=&354.060\\[1ex]x_{2}&=354.06-{\frac {(-3.1269)^{2}}{2\times 354.06}}&&=&354.046\end{aligned}}$$

Поразрядный расчет

Это метод нахождения каждой цифры квадратного корня в последовательности. Этот метод основан на биномиальной теореме и, по сути, на обратном алгоритме решения $(x+y)^{2}=x^{2}+2xy+y^{2}$. Он медленнее вавилонского метода, но имеет ряд преимуществ:

• Это может быть проще для ручных расчетов.
• Каждая найденная цифра корня заведомо верна, т. е. ее не нужно менять в дальнейшем.
• Если квадратный корень имеет расширение, которое завершается, алгоритм завершается после того, как будет найдена последняя цифра. Таким образом, его можно использовать для проверки того, является ли данное целое число квадратным .
• Алгоритм работает для любой базы , и естественно, то, как он будет действовать, зависит от выбранной базы.

Недостатками являются:

• Это становится неуправляемым для более высоких корней.
• Он не терпит неточных догадок или подсчетов; такие ошибки приводят к тому, что каждая следующая цифра результата оказывается неверной, в отличие от метода Ньютона , который самостоятельно исправляет любые ошибки аппроксимации.
• Хотя поразрядные вычисления достаточно эффективны на бумаге, они слишком дороги для программных реализаций. Каждая итерация включает в себя большие числа и требует больше памяти, но увеличивает ответ только на одну правильную цифру. Таким образом, алгоритму требуется больше времени для каждой дополнительной цифры.

Кости Нейпира включают в себя средства для выполнения этого алгоритма. Алгоритм сдвига n-й корня степени является обобщением этого метода.

Основной принцип

Сначала рассмотрим случай нахождения квадратного корня из числа Z , то есть квадрата двузначного числа XY , где X — цифра десятков, а Y — цифра единиц. Конкретно:

$$Z=\left(10X+Y\right)^{2}=100X^{2}+20XY+Y^{2}$$

используя поразрядный алгоритм, мы сначала определяем значение X. Теперь , X — самая большая цифра такая, что X ² меньше или равно Z , из которого мы удалили две крайние правые цифры.

На следующей итерации мы соединяем цифры в пары, умножаем X на 2 и помещаем его на десятое место, пытаясь выяснить, каково Y. значение

Поскольку это простой случай, когда ответом является идеальный квадратный корень XY , алгоритм на этом останавливается.

Далее ту же идею можно распространить на любое произвольное вычисление квадратного корня. Предположим, мы можем найти квадратный корень из N , выразив его как сумму n положительных чисел таких, что

$$N=\left(a_{1}+a_{2}+a_{3}+\dots +a_{n}\right)^{2}.$$

Повторно применяя базовую идентичность

$$(x+y)^{2}=x^{2}+2xy+y^{2},$$

член правой части можно расширить как

$${\begin{aligned}&(a_{1}+a_{2}+a_{3}+\dotsb +a_{n})^{2}\\=&\,a_{1}^{2}+2a_{1}a_{2}+a_{2}^{2}+2(a_{1}+a_{2})a_{3}+a_{3}^{2}+\dots +a_{n-1}^{2}+2\left(\sum _{i=1}^{n-1}a_{i}\right)a_{n}+a_{n}^{2}\\=&\,a_{1}^{2}+[2a_{1}+a_{2}]a_{2}+[2(a_{1}+a_{2})+a_{3}]a_{3}+\dots +\left[2\left(\sum _{i=1}^{n-1}a_{i}\right)+a_{n}\right]a_{n}.\end{aligned}}$$

Это выражение позволяет нам найти квадратный корень, последовательно угадывая значения $a_{i}$с. Предположим, что числа $a_{1},\ldots ,a_{m-1}$ уже угаданы, то m -й член правой части приведенного выше суммирования определяется выражением $Y_{m}=\left[2P_{m-1}+a_{m}\right]a_{m},$ где ${\textstyle P_{m-1}=\sum _{i=1}^{m-1}a_{i}}$ — это приблизительный квадратный корень, найденный на данный момент. Теперь каждая новая догадка $a_{m}$ должно удовлетворять рекурсии

$$X_{m}=X_{m-1}-Y_{m},$$

такой, что $X_{m}\geq 0$ для всех $1\leq m\leq n,$ с инициализацией $X_{0}=N.$ Когда $X_{n}=0,$ найден точный квадратный корень; если нет, то сумма $a_{i}$s дает подходящее приближение квадратного корня, при этом $X_{n}$ является ошибкой аппроксимации.

Например, в десятичной системе счисления имеем

$$N=\left(a_{1}\cdot 10^{n-1}+a_{2}\cdot 10^{n-2}+\cdots +a_{n-1}\cdot 10+a_{n}\right)^{2},$$

где $10^{n-i}$ являются заполнителями и коэффициентами $a_{i}\in \{0,1,2,\ldots ,9\}$. На любом m-м этапе вычисления квадратного корня найденный на данный момент приблизительный корень $P_{m-1}$ и член суммирования $Y_{m}$ даны

$$P_{m-1}=\sum _{i=1}^{m-1}a_{i}\cdot 10^{n-i}=10^{n-m+1}\sum _{i=1}^{m-1}a_{i}\cdot 10^{m-i-1},$$

$$Y_{m}=\left[2P_{m-1}+a_{m}\cdot 10^{n-m}\right]a_{m}\cdot 10^{n-m}=\left[20\sum _{i=1}^{m-1}a_{i}\cdot 10^{m-i-1}+a_{m}\right]a_{m}\cdot 10^{2(n-m)}.$$

Здесь, поскольку позиционное значение $Y_{m}$ является четной степенью 10, нам нужно работать только с парой старших цифр оставшегося члена $X_{m-1}$ на любом m-м этапе. В разделе ниже описана эта процедура.

Очевидно, что аналогичный метод можно использовать для вычисления квадратного корня в других системах счисления, кроме десятичной. Например, нахождение квадратного корня по цифрам в двоичной системе счисления весьма эффективно, поскольку значение $a_{i}$ ищется из меньшего набора двоичных цифр {0,1}. Это ускоряет вычисление, поскольку на каждом этапе значение $Y_{m}$ либо $Y_{m}=0$ для $a_{m}=0$ или $Y_{m}=2P_{m-1}+1$ для $a_{m}=1$. Тот факт, что у нас есть только два возможных варианта $a_{m}$ также осуществляет процесс определения стоимости $a_{m}$ на m -ом этапе расчета проще. Это потому, что нам нужно только проверить, $Y_{m}\leq X_{m-1}$ для $a_{m}=1.$ Если это условие выполнено, то принимаем $a_{m}=1$; если нет, то $a_{m}=0.$ Кроме того, в вычислениях помогает тот факт, что умножение на 2 выполняется сдвигом битов влево.

Десятичная дробь (основание 10)

Запишите исходное число в десятичной форме. Числа записываются аналогично алгоритму длинного деления , и, как и при длинном делении, в строке выше будет записан корень. Теперь разделите цифры на пары, начиная с десятичной точки и идя влево и вправо. Десятичная точка корня будет находиться над десятичной точкой квадрата. Над каждой парой цифр квадрата появится одна цифра корня.

Начиная с самой левой пары цифр, выполните следующую процедуру для каждой пары:

1. Начиная слева, снесите самую значащую (крайнюю левую) пару еще не использованных цифр (если все цифры были использованы, напишите «00») и запишите их справа от остатка от предыдущего шага (на первом шаг, остатка не будет). Другими словами, умножьте остаток на 100 и сложите две цифры. Это будет текущее значение c .
2. Найдите p , y и x следующим образом:
   • Пусть p будет частью найденного на данный момент корня , игнорируя любую десятичную точку. (Для первого шага p = 0.)
   • Определите наибольшую цифру x такую, что $x(20p+x)\leq c$. Мы будем использовать новую переменную y = x (20 p + x ).
     • Примечание. 20 p + x — это просто удвоенное число p цифрой x . с добавленной справа
     • Примечание: x можно найти, угадав, что такое c /(20· p ), и выполнив пробное вычисление y , а затем, x . при необходимости, увеличив или уменьшив
   • Поместите цифру $x$ как следующая цифра корня, т. е. выше двух цифр квадрата, который вы только что сбили. Таким образом, следующим p будет старое p, умноженное на 10 плюс x .
3. Вычтите y из c, чтобы образовать новый остаток.
4. Если остаток равен нулю и больше нет цифр, которые нужно сбить, то алгоритм завершается. В противном случае вернитесь к шагу 1 для следующей итерации.

Примеры

Найдите квадратный корень из 152,2756.

          1  2. 3  4 
       /
     \/  01 52.27 56

         01                   1*1 <= 1 < 2*2                 x=1
         01                     y = x*x = 1*1 = 1
         00 52                22*2 <= 52 < 23*3              x=2
         00 44                  y = (20+x)*x = 22*2 = 44
            08 27             243*3 <= 827 < 244*4           x=3
            07 29               y = (240+x)*x = 243*3 = 729
               98 56          2464*4 <= 9856 < 2465*5        x=4
               98 56            y = (2460+x)*x = 2464*4 = 9856
               00 00          Algorithm terminates: Answer=12.34

Двоичная система счисления (основание 2)

В этом разделе используется формализм из раздела поразрядных вычислений выше , с небольшими вариациями, которые мы допускаем. $N^{2}=(a_{n}+\dotsb +a_{0})^{2}$, с каждым $a_{m}=2^{m}$ или $a_{m}=0$.
Мы повторяем все $2^{m}$, от $2^{n}$ вплоть до $2^{0}$и построим приближенное решение $P_{m}=a_{n}+a_{n-1}+\ldots +a_{m}$, сумма всех $a_{i}$ для которого мы определили стоимость.
Чтобы определить, если $a_{m}$ равно $2^{m}$ или $0$, мы позволяем $P_{m}=P_{m+1}+2^{m}$. Если $P_{m}^{2}\leq N^{2}$ (т.е. квадрат нашего приближенного решения, включая $2^{m}$ не превышает целевой квадрат), тогда $a_{m}=2^{m}$, в противном случае $a_{m}=0$ и $P_{m}=P_{m+1}$.
Чтобы избежать квадратуры $P_{m}$ на каждом этапе мы сохраняем разницу $X_{m}=N^{2}-P_{m}^{2}$ и постепенно обновлять его, установив $X_{m}=X_{m+1}-Y_{m}$ с $Y_{m}=P_{m}^{2}-P_{m+1}^{2}=2P_{m+1}a_{m}+a_{m}^{2}$.
Изначально мы установили $a_{n}=P_{n}=2^{n}$ для крупнейшего $n$ с $(2^{n})^{2}=4^{n}\leq N^{2}$.

В качестве дополнительной оптимизации мы сохраняем $P_{m+1}2^{m+1}$ и $(2^{m})^{2}$, два члена $Y_{m}$ в случае, если $a_{m}$ ненулевое значение в отдельных переменных $c_{m}$, $d_{m}$:

$$c_{m}=P_{m+1}2^{m+1}$$

$$d_{m}=(2^{m})^{2}$$

$$Y_{m}={\begin{cases}c_{m}+d_{m}&{\text{if }}a_{m}=2^{m}\\0&{\text{if }}a_{m}=0\end{cases}}$$

$c_{m}$ и $d_{m}$ можно эффективно обновлять на каждом этапе:

$$c_{m-1}=P_{m}2^{m}=(P_{m+1}+a_{m})2^{m}=P_{m+1}2^{m}+a_{m}2^{m}={\begin{cases}c_{m}/2+d_{m}&{\text{if }}a_{m}=2^{m}\\c_{m}/2&{\text{if }}a_{m}=0\end{cases}}$$

$$d_{m-1}={\frac {d_{m}}{4}}$$

Обратите внимание, что:

$$c_{-1}=P_{0}2^{0}=P_{0}=N,$$

это конечный результат, возвращаемый функцией ниже.

Реализация этого алгоритма на C:

int32_t isqrt(int32_t n) {
    assert(("sqrt input should be non-negative", n > 0));

    // X_(n+1)
    int32_t x = n;

    // c_n
    int32_t c = 0;

    // d_n which starts at the highest power of four <= n
    int32_t d = 1 << 30; // The second-to-top bit is set.
                         // Same as ((unsigned) INT32_MAX + 1) / 2.
    while (d > n) {
        d >>= 2;
    }

    // for dₙ … d₀
    while (d != 0) {
        if (x >= c + d) {      // if X_(m+1) ≥ Y_m then a_m = 2^m
            x -= c + d;        // X_m = X_(m+1) - Y_m
            c = (c >> 1) + d;  // c_(m-1) = c_m/2 + d_m (a_m is 2^m)
        }
        else {
            c >>= 1;           // c_(m-1) = c_m/2      (aₘ is 0)
        }
        d >>= 2;               // d_(m-1) = d_m/4
    }
    return c;                  // c_(-1)
}

Более быстрые алгоритмы в двоичной, десятичной или любой другой системе счисления могут быть реализованы с помощью справочных таблиц, что фактически позволяет получить больше места для хранения за счет сокращения времени выполнения .

Экспоненциальное тождество

Карманные калькуляторы обычно реализуют хорошие процедуры для вычисления экспоненциальной функции и натурального логарифма , а затем вычисления квадратного корня из S, используя тождество, найденное с использованием свойств логарифмов ( $\ln x^{n}=n\ln x$) и экспоненты ( $e^{\ln x}=x$):

$${\sqrt {S}}=e^{{\frac {1}{2}}\ln S}.$$

Знаменатель дроби соответствует корню n- й степени. В приведенном выше случае знаменатель равен 2, следовательно, уравнение указывает, что необходимо найти квадратный корень. Тот же идентификатор используется при вычислении квадратных корней с помощью таблиц логарифмов или логарифмических правил .

Итерационный метод с двумя переменными

Этот метод применим для нахождения квадратного корня из $0<S<3\,\!$ и сходится лучше всего для $S\approx 1$. Однако это не является реальным ограничением для компьютерных вычислений, поскольку в представлениях с плавающей запятой по основанию 2 и с фиксированной запятой умножить тривиально. $S\,\!$ в целой степени 4, и, следовательно, ${\sqrt {S}}$ на соответствующую степень 2, путем изменения показателя степени или сдвига соответственно. Поэтому, $S\,\!$ можно переместить в диапазон ${\textstyle {\tfrac {1}{2}}\leq S<2}$. Более того, следующий метод не использует общего деления, а только сложения, вычитания, умножения и деления на степени двойки, которые также тривиально реализовать. Недостатком метода является накопление числовых ошибок, в отличие от итеративных методов с одной переменной, таких как вавилонский.

Шаг инициализации этого метода:

$${\begin{aligned}a_{0}&=S\\c_{0}&=S-1\end{aligned}}$$

в то время как итеративные шаги читаются

$${\begin{aligned}a_{n+1}&=a_{n}-a_{n}c_{n}/2\\c_{n+1}&=c_{n}^{2}(c_{n}-3)/4\end{aligned}}$$

Затем, $a_{n}\to {\sqrt {S}}$ (пока $c_{n}\to 0$).

Конвергенция $c_{n}\,\!$, и, следовательно, также $a_{n}\,\!$, является квадратичным.

Доказательство метода довольно простое. Сначала перепишем итеративное определение $c_{n}$ как

$$1+c_{n+1}=(1+c_{n})(1-{\tfrac {1}{2}}c_{n})^{2}.$$

Тогда несложно по индукции доказать, что

$$S(1+c_{n})=a_{n}^{2}$$

и, следовательно, конвергенция $a_{n}\,\!$ к желаемому результату ${\sqrt {S}}$ обеспечивается за счет сближения $c_{n}\,\!$ до 0, что, в свою очередь, следует из $-1<c_{0}<2\,\!$.

Этот метод был разработан около 1950 года М.В. Уилксом , Д.Д. Уилером и С. Гиллом. для использования на EDSAC , одном из первых электронных компьютеров. Позже метод был обобщен, что позволило вычислять неквадратные корни.

корней

Ниже приведены итерационные методы нахождения обратного квадратного корня из S, который равен $1/{\sqrt {S}}$. Как только он будет найден, найдите ${\sqrt {S}}$ простым умножением: ${\sqrt {S}}=S\cdot (1/{\sqrt {S}})$. Эти итерации включают только умножение, а не деление. Поэтому они быстрее, чем вавилонский метод . Однако они не стабильны. Если начальное значение не близко к обратному квадратному корню, итерации будут расходиться от него, а не сходиться к нему. Поэтому может быть полезно выполнить итерацию вавилонского метода с грубой оценкой, прежде чем начинать применять эти методы.

• Применение метода Ньютона к уравнению $(1/x^{2})-S=0$ создает метод, который сходится квадратично, используя три умножения за шаг:
  $$x_{n+1}={\frac {x_{n}}{2}}\cdot (3-S\cdot x_{n}^{2})=x_{n}\cdot \left({\frac {3}{2}}-{\frac {S}{2}}\cdot x_{n}^{2}\right).$$
• Другая итерация получается методом Галлея , который является методом Хаусхолдера второго порядка. Это сходится кубически , но включает пять умножений на итерацию:
  $$y_{n}=S\cdot x_{n}^{2},$$
  и
  $$x_{n+1}={\frac {x_{n}}{8}}\cdot (15-y_{n}\cdot (10-3\cdot y_{n}))=x_{n}\cdot \left({\frac {15}{8}}-y_{n}\cdot \left({\frac {10}{8}}-{\frac {3}{8}}\cdot y_{n}\right)\right).$$
• При выполнении арифметических операций с фиксированной запятой умножение на 3 и деление на 8 можно реализовать с помощью сдвигов и сложений. При использовании чисел с плавающей запятой метод Галлея можно сократить до четырех умножений на итерацию путем предварительного вычисления. ${\textstyle {\sqrt {3/8}}S}$ и корректируем все остальные константы для компенсации:
  $$y_{n}={\sqrt {\frac {3}{8}}}S\cdot x_{n}^{2},$$
  и
  $$x_{n+1}=x_{n}\cdot \left({\frac {15}{8}}-y_{n}\cdot \left({\sqrt {\frac {25}{6}}}-y_{n}\right)\right).$$

Алгоритм Гольдшмидта

Некоторые компьютеры используют алгоритм Гольдшмидта для одновременного расчета. ${\sqrt {S}}$ и $1/{\sqrt {S}}$. Алгоритм Гольдшмидта находит ${\sqrt {S}}$ быстрее, чем итерация Ньютона-Рафсона на компьютере с объединенной командой умножения-сложения и либо конвейерным блоком с плавающей запятой, либо двумя независимыми блоками с плавающей запятой.

Начинается первый способ написания алгоритма Гольдшмидта.

$b_{0}=S$

$Y_{0}\approx 1/{\sqrt {S}}$ (обычно с использованием поиска по таблице)

$y_{0}=Y_{0}$

$x_{0}=Sy_{0}$

и повторяет

$${\begin{aligned}b_{n+1}&=b_{n}Y_{n}^{2}\\Y_{n+1}&={\tfrac {1}{2}}(3-b_{n+1})\\x_{n+1}&=x_{n}Y_{n+1}\\y_{n+1}&=y_{n}Y_{n+1}\end{aligned}}$$

до $b_{i}$ достаточно близко к 1 или фиксированному числу итераций. Итерации сходятся к

$$\lim _{n\to \infty }x_{n}={\sqrt {S}},$$

и

$$\lim _{n\to \infty }y_{n}=1/{\sqrt {S}}.$$

Обратите внимание, что можно опустить либо $x_{n}$ и $y_{n}$ из вычислений, и если оба желательны, то $x_{n}=Sy_{n}$ может использоваться в конце, а не вычисляться на каждой итерации.

Вторая форма, использующая объединенные операции умножения-сложения , начинается

$y_{0}\approx 1/{\sqrt {S}}$ (обычно с использованием поиска по таблице)

$x_{0}=Sy_{0}$

$h_{0}={\tfrac {1}{2}}y_{0}$

и повторяет

$${\begin{aligned}r_{n}&=0.5-x_{n}h_{n}\\x_{n+1}&=x_{n}+x_{n}r_{n}\\h_{n+1}&=h_{n}+h_{n}r_{n}\end{aligned}}$$

до $r_{i}$ достаточно близко к 0 или фиксированному числу итераций. Это сходится к

$$\lim _{n\to \infty }x_{n}={\sqrt {S}},$$

и

$$\lim _{n\to \infty }2h_{n}=1/{\sqrt {S}}.$$

Серия Тейлора

Если N является приближением к ${\sqrt {S}}$лучшее приближение можно найти, используя ряд Тейлора функции квадратного корня :

$${\sqrt {N^{2}+d}}=N\sum _{n=0}^{\infty }{\frac {(-1)^{n}(2n)!}{(1-2n)n!^{2}4^{n}}}{\frac {d^{n}}{N^{2n}}}=N\left(1+{\frac {d}{2N^{2}}}-{\frac {d^{2}}{8N^{4}}}+{\frac {d^{3}}{16N^{6}}}-{\frac {5d^{4}}{128N^{8}}}+\cdots \right)$$

В итерационном методе порядок сходимости равен количеству используемых терминов. С двумя терминами он идентичен вавилонскому методу . При трех членах каждая итерация занимает почти столько же операций, сколько и приближение Бахшали , но сходится медленнее. Поэтому это не особенно эффективный способ расчета. Чтобы максимизировать скорость сходимости, выберите N так, чтобы ${\frac {|d|}{N^{2}}}\,$ как можно меньше.

дроби

См. также: Решение квадратных уравнений с цепными дробями.

Представление действительного числа в виде непрерывной дроби можно использовать вместо его десятичного или двоичного разложения, и это представление обладает тем свойством, что квадратный корень любого рационального числа (которое еще не является точным квадратом) имеет периодическое, повторяющееся разложение, аналогичное как рациональные числа имеют повторяющиеся расширения в десятичной системе счисления.

Квадратичные иррациональные числа (числа вида ${\frac {a+{\sqrt {b}}}{c}}$, где a , b и c — целые числа), и, в частности, квадратные корни из целых чисел, имеют периодические цепные дроби . Иногда требуется найти не числовое значение квадратного корня, а его разложение в непрерывную дробь и, следовательно, его рациональное приближение. Пусть S — положительное число, для которого нам необходимо найти квадратный корень. Тогда, предположив, что a — число, которое служит в качестве первоначального предположения, а r — остаточный член, мы можем написать $S=a^{2}+r.$ Поскольку у нас есть $S-a^{2}=({\sqrt {S}}+a)({\sqrt {S}}-a)=r$, мы можем выразить квадратный корень из S как

$${\sqrt {S}}=a+{\frac {r}{a+{\sqrt {S}}}}.$$

Применяя это выражение для ${\sqrt {S}}$ к знаменателю дроби, имеем

$${\sqrt {S}}=a+{\frac {r}{a+(a+{\frac {r}{a+{\sqrt {S}}}})}}=a+{\frac {r}{2a+{\frac {r}{a+{\sqrt {S}}}}}}.$$

Компактное обозначение

Расширение числителя и знаменателя для цепных дробей (см. слева) сложно записывать, а также встраивать в системы форматирования текста. Поэтому математики разработали несколько альтернативных обозначений, например

$${\sqrt {S}}=a+{\frac {r}{2a+}}\,{\frac {r}{2a+}}\,{\frac {r}{2a+}}\cdots$$

Когда $r=1$ повсюду используются еще более компактные обозначения:

$$[a;2a,2a,2a,\cdots ]$$

Для повторяющихся непрерывных дробей (что делают все квадратные корни из неполных квадратов) повторение представляется только один раз, с надчеркиванием, обозначающим непрерывное повторение перечеркнутой части:

$$[a;{\overline {2a}}]$$

Для √ 2 значение $a$ равно 1, поэтому его представление:

$$[1;{\overline {2}}]$$

Действуя таким образом, мы получаем обобщенную цепную дробь для квадратного корня как

$${\sqrt {S}}=a+{\cfrac {r}{2a+{\cfrac {r}{2a+{\cfrac {r}{2a+\ddots }}}}}}$$

Первый шаг к вычислению такой дроби Чтобы получить корень, нужно выполнить числовые замены корня желаемого числа и выбранного количества знаменателей. Например, в канонической форме $r$ а для √ 2 равно 1 , $a$ равно 1, поэтому числовая цепная дробь для трех знаменателей равна:

$${\sqrt {2}}\approx 1+{\cfrac {1}{2+{\cfrac {1}{2+{\cfrac {1}{2}}}}}}$$

Шаг 2 — сократить непрерывную дробь снизу вверх по одному знаменателю, чтобы получить рациональную дробь, числитель и знаменатель которой являются целыми числами. Приведение происходит следующим образом (беря первые три знаменателя):

$${\begin{aligned}1+{\cfrac {1}{2+{\cfrac {1}{2+{\cfrac {1}{2}}}}}}&=1+{\cfrac {1}{2+{\cfrac {1}{\frac {5}{2}}}}}\\&=1+{\cfrac {1}{2+{\cfrac {2}{5}}}}=1+{\cfrac {1}{\frac {12}{5}}}\\&=1+{\cfrac {5}{12}}={\frac {17}{12}}\end{aligned}}$$

Наконец (шаг 3) разделите числитель на знаменатель рациональной дроби, чтобы получить приблизительное значение корня:

$$17\div 12=1.42$$

округляется до трех знаков точности.

Фактическое значение √ 2 составляет от 1,41 до трех значащих цифр. Относительная ошибка составляет 0,17%, поэтому рациональная дробь имеет точность почти три знака. Увеличение количества знаменателей дает более качественные приближения: четыре знаменателя дают дробь ${\frac {41}{29}}=1.4137$, с почти 4-значной точностью и т. д.

Ниже приведены примеры квадратных корней, их простых цепных дробей и их первых членов, называемых сходящимися , до знаменателя 99 включительно:

√ S	~десятичный	непрерывная дробь	сходящийся
√ 2	1.41421	$[1;{\overline {2}}]$	${\frac {3}{2}},{\frac {7}{5}},{\frac {17}{12}},{\frac {41}{29}},{\frac {99}{70}}$
√ 3	1.73205	$[1;{\overline {1,2}}]$	${\frac {2}{1}},{\frac {5}{3}},{\frac {7}{4}},{\frac {19}{11}},{\frac {26}{15}},{\frac {71}{41}},{\frac {97}{56}}$
√ 5	2.23607	$[2;{\overline {4}}]$	${\frac {9}{4}},{\frac {38}{17}},{\frac {161}{72}}$
√ 6	2.44949	$[2;{\overline {2,4}}]$	${\frac {5}{2}},{\frac {22}{9}},{\frac {49}{20}},{\frac {218}{89}}$
√ 10	3.16228	$[3;{\overline {6}}]$	${\frac {19}{6}},{\frac {117}{37}}$
${\sqrt {\pi }}$	1.77245	$[1;1,3,2,1,1,6...]$	${\frac {2}{1}},{\frac {7}{4}},{\frac {16}{9}},{\frac {23}{13}},{\frac {39}{22}}$
${\sqrt {e}}$	1.64872	$[1;1,1,1,5,1,1...]$	${\frac {2}{1}},{\frac {3}{2}},{\frac {5}{3}},{\frac {28}{17}},{\frac {33}{20}},{\frac {61}{37}}$
${\sqrt {\phi }}$	1.27202	$[1;3,1,2,11,3,7...]$	${\frac {4}{3}},{\frac {5}{4}},{\frac {14}{11}}$

В общем, чем больше знаменатель рациональной дроби, тем лучше приближение. Также можно показать, что усечение непрерывной дроби дает рациональную дробь, которая является лучшим приближением к корню любой дроби со знаменателем, меньшим или равным знаменателю этой дроби - например, нет дроби со знаменателем, меньшим или равным 70 является таким же хорошим приближением к √ 2, как и 99/70.

Приближения, зависящие от представления с плавающей запятой

Число представлено в формате с плавающей запятой как $m\times b^{p}$ который также называется научной нотацией . Его квадратный корень ${\sqrt {m}}\times b^{p/2}$ и аналогичные формулы применимы для кубических корней и логарифмов. На первый взгляд, это не улучшение простоты, но предположим, что требуется только приближение: тогда просто $b^{p/2}$ это хорошо на порядок. Далее учтите, что некоторые степени p будут нечетными, например, для 3141,59 = 3,14159 × 10. ³ вместо того, чтобы иметь дело с дробными степенями основания, умножьте мантиссу на основание и вычтите единицу из степени, чтобы сделать ее четной. Скорректированное представление станет эквивалентом 31,4159 × 10. ² так что квадратный корень будет √ 31,4159 × 10 ¹ .

Если взять целую часть скорректированной мантиссы, могут быть только значения от 1 до 99, и их можно использовать в качестве индекса в таблице из 99 заранее вычисленных квадратных корней для завершения оценки. Компьютеру, использующему шестнадцатеричное основание, потребовалась бы таблица большего размера, но компьютеру, использующему основание два, потребовалось бы только три записи: возможные биты целой части скорректированной мантиссы равны 01 (даже при том, что степени не было никакого сдвига, учитывая, что нормализованная число с плавающей запятой всегда имеет ненулевую старшую цифру) или, если степень была нечетной, 10 или 11, это первые два бита исходной мантиссы. Таким образом, 6,25 = 110,01 в двоичном формате, нормированном на 1,1001 × 2. ² четная степень, поэтому парные биты мантиссы равны 01, а 0,625 = 0,101 в двоичном формате нормализуется до 1,01 × 2. ⁻¹ нечетная степень, поэтому корректировка равна 10,1 × 2 ⁻² а парные биты равны 10. Обратите внимание, что младший бит степени повторяется в старшем бите парной мантиссы. Младший бит четной степени равен нулю, и скорректированная мантисса начинается с 0, тогда как для нечетной степени этот бит равен единице, а скорректированная мантисса начинается с 1. Таким образом, когда степень уменьшается вдвое, это как если бы Младший бит сдвигается и становится первым битом парной мантиссы.

Таблицу, содержащую всего три записи, можно расширить за счет включения дополнительных битов мантиссы. Однако при использовании компьютеров вместо интерполяции в таблицу часто лучше найти более простой расчет, дающий эквивалентные результаты. Теперь все зависит от точных деталей формата представления, а также от того, какие операции доступны для доступа к частям числа и манипулирования ими. Например, Фортран предлагает EXPONENT(x) Функция получения власти. Усилия, затраченные на разработку хорошего начального приближения, должны окупиться за счет исключения дополнительных итераций процесса уточнения, которые потребовались бы для плохого приближения. Поскольку их немного (одна итерация требует деления, сложения и деления пополам), ограничение является серьезным.

Многие компьютеры следуют представлению IEEE (или достаточно похожему), и можно получить очень быстрое приближение к квадратному корню для запуска метода Ньютона. Следующий метод основан на том факте, что формат с плавающей запятой (по основанию два) приближается к логарифму по основанию 2. То есть $\log _{2}(m\times 2^{p})=p+\log _{2}(m)$

Таким образом, для 32-битного числа с плавающей запятой одинарной точности в формате IEEE (где, в частности, степень имеет смещение 127, добавленное для представленной формы) вы можете получить приблизительный логарифм, интерпретируя его двоичное представление как 32-битное целое число, масштабируя это по $2^{-23}$, и удаляя смещение 127, т.е.

$$x_{\text{int}}\cdot 2^{-23}-127\approx \log _{2}(x).$$

Например, 1.0 представлен шестнадцатеричным числом 0x3F800000, которое будет обозначать $1065353216=127\cdot 2^{23}$ если принять за целое число. Используя формулу выше, вы получаете $1065353216\cdot 2^{-23}-127=0$, как и ожидалось от $\log _{2}(1.0)$. Аналогичным образом вы получаете 0,5 из 1,5 (0x3FC00000).

Чтобы получить квадратный корень, разделите логарифм на 2 и преобразуйте значение обратно. Следующая программа демонстрирует эту идею. Младшему биту экспоненты намеренно разрешено распространяться на мантиссу. Один из способов оправдать шаги в этой программе — предположить, что $b$ - смещение показателя и $n$ — количество явно сохраненных битов в мантиссе, а затем покажите, что

$$\left(\left({\tfrac {1}{2}}\left(x_{\text{int}}/2^{n}-b\right)\right)+b\right)\cdot 2^{n}={\tfrac {1}{2}}\left(x_{\text{int}}-2^{n}\right)+\left({\tfrac {1}{2}}\left(b+1\right)\right)\cdot 2^{n}.$$

/* Assumes that float is in the IEEE 754 single precision floating point format */
#include <stdint.h>
float sqrt_approx(float z)
{
	union { float f; uint32_t i; } val = {z};	/* Convert type, preserving bit pattern */
	/*
	 * To justify the following code, prove that
	 *
	 * ((((val.i / 2^m) - b) / 2) + b) * 2^m = ((val.i - 2^m) / 2) + ((b + 1) / 2) * 2^m)
	 *
	 * where
	 *
	 * b = exponent bias
	 * m = number of mantissa bits
	 */
	val.i -= 1 << 23;	/* Subtract 2^m. */
	val.i >>= 1;		/* Divide by 2. */
	val.i += 1 << 29;	/* Add ((b + 1) / 2) * 2^m. */

	return val.f;		/* Interpret again as float */
}

Три математические операции, составляющие ядро ​​вышеуказанной функции, могут быть выражены в одной строке. Для уменьшения максимальной относительной погрешности можно добавить дополнительную настройку. Итак, три операции, не считая приведения, можно переписать как

	val.i = (1 << 29) + (val.i >> 1) - (1 << 22) + a;

где a — погрешность корректировки ошибок аппроксимации. Например, при a = 0 результаты точны для четных степеней 2 (например, 1,0), но для других чисел результаты будут немного завышены (например, 1,5 для 2,0 вместо 1,414... с ошибкой 6%). При a = −0x4B0D2 максимальная относительная погрешность минимизируется до ±3,5%.

Если аппроксимация должна использоваться для первоначального предположения метода Ньютона для уравнения $(1/x^{2})-S=0$, то предпочтительна обратная форма, показанная в следующем разделе.

обратная квадратному корню

Основная статья: Быстрый обратный квадратный корень

Ниже приведен вариант описанной выше процедуры, который можно использовать для вычисления обратной величины квадратного корня, т.е. $x^{-1/2}$ вместо этого его написал Грег Уолш. Приближение целочисленного сдвига дало относительную ошибку менее 4%, а ошибка упала еще до 0,15% при одной итерации метода Ньютона в следующей строке. В компьютерной графике это очень эффективный способ нормализации вектора.

float invSqrt(float x) {
    float xhalf = 0.5f * x;
    union {
        float x;
        int i;
    } u;
    u.x = x;
    u.i = 0x5f375a86 - (u.i >> 1);
    /* The next line can be repeated any number of times to increase accuracy */
    u.x = u.x * (1.5f - xhalf * u.x * u.x);
    return u.x;
}

Некоторые аппаратные средства СБИС реализуют обратный квадратный корень с использованием оценки полинома второй степени с последующей итерацией Гольдшмидта .

Отрицательный или комплексный квадрат

Если S < 0, то его главный квадратный корень равен

$${\sqrt {S}}={\sqrt {\vert S\vert }}\,\,i\,.$$

Если S = ​​a + bi , где a и b вещественные и b ≠ 0, то его главный квадратный корень равен

$${\sqrt {S}}={\sqrt {\frac {\vert S\vert +a}{2}}}\,+\,\operatorname {sgn}(b){\sqrt {\frac {\vert S\vert -a}{2}}}\,\,i\,.$$

В этом можно убедиться, возведя корень в квадрат. Здесь

$$\vert S\vert ={\sqrt {a^{2}+b^{2}}}$$

является модулем S ​ . Главный квадратный корень комплексного числа определяется как корень с неотрицательной действительной частью.

См. также

• Алгоритм альфа-макс плюс бета-мин
• алгоритм n-го корня

Библиография

• Абрамовиц, Милтонн; Стегун, Ирен А. (1964). Справочник математических функций с формулами, графиками и математическими таблицами . Публикации Курьера Дувра. п. 17. ISBN  978-0-486-61272-0 .
• Бейли, Дэвид; Борвейн, Джонатан (2012). «Древнеиндийские квадратные корни: упражнение по судебной палеоматематике» (PDF) . Американский математический ежемесячник . Том. 119, нет. 8. стр. 646–657 . Проверено 14 сентября 2017 г.
• Кэмпбелл-Келли, Мартин (сентябрь 2009 г.). «Происхождение вычислительной техники». Научный американец . 301 (3): 62–69. Бибкод : 2009SciAm.301c..62C . doi : 10.1038/scientificamerican0909-62 . JSTOR   26001527 . ПМИД   19708529 .
• Кук, Роджер (2008). Классическая алгебра: ее природа, происхождение и использование . Джон Уайли и сыновья. п. 59. ИСБН  978-0-470-25952-8 .
• Фаулер, Дэвид; Робсон, Элеонора (1998). «Приближения квадратного корня в древневавилонской математике: YBC 7289 в контексте» (PDF) . История Математики . 25 (4): 376. doi : 10.1006/hmat.1998.2209 .
• Гауэр, Джон К. (1958). «Заметки об итеративном методе извлечения корня» . Компьютерный журнал . 1 (3): 142–143. дои : 10.1093/comjnl/1.3.142 .
• Джексон, Теренс (01 июля 2011 г.). «95.42 Иррациональные квадратные корни натуральных чисел — геометрический подход» . Математический вестник . 95 (533): 327–330. дои : 10.1017/S0025557200003193 . ISSN   0025-5572 . S2CID   123995083 .
• Гай, Мартин; УКК (1985). «Быстрое извлечение квадратного корня из целых чисел с помощью алгоритма счетов мистера Ву (в архиве)» . Архивировано из оригинала 06 марта 2012 г.
• Хит, Томас (1921). История греческой математики, Vol. 2 . Оксфорд: Кларендон Пресс. стр. 323–324 .
• Ломонт, Крис (2003). «Быстрый обратный квадратный корень» (PDF) .
• Маркштейн, Питер (ноябрь 2004 г.). Деление программного обеспечения и квадратный корень с использованием алгоритмов Гольдшмидта (PDF) . 6-я конференция «Действительные числа и компьютеры» . Дагштуль , Германия. CiteSeerX   10.1.1.85.9648 .
• Пинейро, Хосе-Алехандро; Диас Бругера, Хавьер (декабрь 2002 г.). «Высокоскоростное вычисление двойной точности обратных чисел, деления, квадратного корня и обратного квадратного корня» . Транзакции IEEE на компьютерах . 51 (12): 1377–1388. дои : 10.1109/TC.2002.1146704 .
• Сардина, Мэнни (2007). «Общий метод извлечения корней с использованием (сложенных) цепных дробей» . Суррей (Великобритания).
• Просто любопытно (5 июня 2018 г.). «Приступаем к рукописи Бахшали» . Просто любопытный блог . Проверено 21 декабря 2020 г.
• Стейнарсон, Арне; Корбит, Данн; Хендри, Мэтью (2003). «Функция целочисленного квадратного корня» .
• Уилкс, М.В. ; Уилер, диджей ; Гилл, С. (1951). Подготовка программ для электронной цифровой вычислительной машины . Оксфорд: Аддисон-Уэсли. стр. 323–324 . OCLC   475783493 .

Внешние ссылки

• Вайсштейн, Эрик В. «Алгоритмы квадратного корня» . Математический мир .
• Квадратные корни путем вычитания
• Алгоритм целочисленного квадратного корня Андрия Радовича
• Алгоритмы персонального калькулятора I: квадратные корни (Уильям Э. Эгберт), Hewlett-Packard Journal (май 1977 г.): стр. 22
• Калькулятор, чтобы узнать квадратный корень