Среднеквадратичное значение

В математике среднеквадратическое значение (сокр. RMS , RMS или rms ) набора чисел представляет собой квадратный корень набора из среднего квадратического значения . Учитывая набор $x_{i}$, его среднеквадратичное значение обозначается либо как $x_{\mathrm {RMS} }$ или $\mathrm {RMS} _{x}$. RMS также известно как среднее квадратичное (обозначается $M_{2}$), частный случай обобщенного среднего . Среднеквадратичное значение непрерывной функции обозначается $f_{\mathrm {RMS} }$ и может быть определен через интеграл от квадрата функции.

Среднеквадратичное значение переменного электрического тока равно значению постоянного постоянного тока , который рассеивает ту же мощность на резистивной нагрузке . В теории оценивания среднеквадратичное отклонение оценщика измеряет, насколько далеко оценщик отклоняется от данных.

Определение

Среднеквадратичное значение набора значений (или непрерывного времени сигнала ) представляет собой квадратный корень из среднего арифметического квадратов значений или квадрата функции, определяющей непрерывный сигнал. В физике среднеквадратичное значение тока также можно определить как «значение постоянного тока, рассеивающего такую ​​же мощность на резисторе».

В случае набора из n значений $\{x_{1},x_{2},\dots ,x_{n}\}$, среднеквадратичное значение

$x_{\text{RMS}}={\sqrt {{\frac {1}{n}}\left({x_{1}}^{2}+{x_{2}}^{2}+\cdots +{x_{n}}^{2}\right)}}.$

Соответствующая формула для непрерывной функции (или формы сигнала) f ( t ), определенной на интервале $T_{1}\leq t\leq T_{2}$ является

$f_{\text{RMS}}={\sqrt {{1 \over {T_{2}-T_{1}}}{\int _{T_{1}}^{T_{2}}{[f(t)]}^{2}\,{\rm {d}}t}}},$

а среднеквадратичное значение функции за все время равно

$f_{\text{RMS}}=\lim _{T\rightarrow \infty }{\sqrt {{1 \over {2T}}{\int _{-T}^{T}{[f(t)]}^{2}\,{\rm {d}}t}}}.$

Среднеквадратическое значение периодической функции за все время равно среднеквадратическому значению одного периода функции. Среднеквадратическое значение непрерывной функции или сигнала можно аппроксимировать, взяв среднеквадратичное значение выборки, состоящей из равноотстоящих друг от друга наблюдений. Кроме того, среднеквадратичное значение различных сигналов также можно определить без математических вычислений , как показал Картрайт.

В случае среднеквадратической статистики случайного процесса ожидаемое значение вместо среднего значения используется .

В обычных формах сигналов

Синусоидальная , прямоугольная , треугольная и пилообразная формы сигналов. В каждом из них центральная линия находится на отметке 0, положительный пик — на отметке 0. $y=A_{1}$ и отрицательный пик находится в $y=-A_{1}$

Импульсная волна прямоугольной формы с коэффициентом заполнения D, соотношение длительности импульса ( $\tau$) и период (Т); показано здесь с = 1.

График зависимости синусоидального напряжения от времени (в градусах), показывающий среднеквадратичное, пиковое (PK) и размах напряжения (PP).

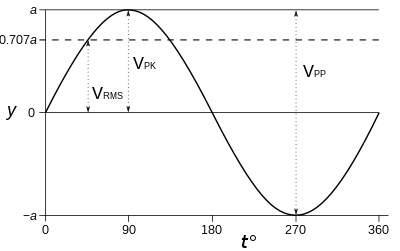
Если форма сигнала представляет собой чистую синусоидальную волну , соотношения между амплитудами (размах размаха, пик) и среднеквадратичным значением фиксированы и известны, как и для любой непрерывной периодической волны. Однако это неверно для сигнала произвольной формы, который не может быть периодическим или непрерывным. Для синусоидальной волны с нулевым средним значением соотношение между среднеквадратичным значением и размахом амплитуды равно:

Пик-пик $=2{\sqrt {2}}\times {\text{RMS}}\approx 2.8\times {\text{RMS}}.$

Для других форм сигналов взаимосвязи не такие, как для синусоидальных волн. Например, для треугольной или пилообразной волны:

Пик-пик $=2{\sqrt {3}}\times {\text{RMS}}\approx 3.5\times {\text{RMS}}.$

Форма волны	Переменные и операторы	среднеквадратичное значение
округ Колумбия	$y=A_{0}\,$	$A_{0}\,$
Синусоидальная волна	$y=A_{1}\sin(2\pi ft)\,$	${\frac {A_{1}}{\sqrt {2}}}$
Прямоугольная волна	$y={\begin{cases}A_{1}&\operatorname {frac} (ft)<0.5\\-A_{1}&\operatorname {frac} (ft)>0.5\end{cases}}$	$A_{1}\,$
Прямоугольная волна со смещением постоянного тока	$y=A_{0}+{\begin{cases}A_{1}&\operatorname {frac} (ft)<0.5\\-A_{1}&\operatorname {frac} (ft)>0.5\end{cases}}$	${\sqrt {A_{0}^{2}+A_{1}^{2}}}\,$
Модифицированная синусоидальная волна	$y={\begin{cases}0&\operatorname {frac} (ft)<0.25\\A_{1}&0.25<\operatorname {frac} (ft)<0.5\\0&0.5<\operatorname {frac} (ft)<0.75\\-A_{1}&\operatorname {frac} (ft)>0.75\end{cases}}$	${\frac {A_{1}}{\sqrt {2}}}$
Треугольная волна	$y=\left|2A_{1}\operatorname {frac} (ft)-A_{1}\right|$	$A_{1} \over {\sqrt {3}}$
Пилообразная волна	$y=2A_{1}\operatorname {frac} (ft)-A_{1}\,$	$A_{1} \over {\sqrt {3}}$
Пульсовая волна	$y={\begin{cases}A_{1}&\operatorname {frac} (ft)<D\\0&\operatorname {frac} (ft)>D\end{cases}}$	$A_{1}{\sqrt {D}}$
Линейная синусоидальная волна	$y=A_{1}\sin(t)-A_{1}\sin \left(t-{\frac {2\pi }{3}}\right)\,$	$A_{1}{\sqrt {\frac {3}{2}}}$
где: y – смещение, это время, f — частота, A i – амплитуда (пиковое значение), D — рабочий цикл или доля периода времени (1/ f ), проведенного в высоком режиме, ( r ) — дробная часть r . frac

В комбинациях сигналов

Сигналы, полученные путем суммирования известных простых сигналов, имеют среднеквадратическое значение, которое является корнем суммы квадратов среднеквадратичных значений компонентов, если сигналы компонентов ортогональны ( то есть, если среднее значение произведения одного простого сигнала на другой равно нулю). для всех пар, кроме времени самого сигнала).

${\text{RMS}}_{\text{Total}}={\sqrt {{\text{RMS}}_{1}^{2}+{\text{RMS}}_{2}^{2}+\cdots +{\text{RMS}}_{n}^{2}}}$

Альтернативно, для сигналов, которые полностью положительно коррелируют или «синфазны» друг с другом, их среднеквадратические значения суммируются напрямую.

Использование

В электротехнике

Напряжение

Дополнительная информация: Среднеквадратичное переменное напряжение.

Особым случаем среднеквадратичного значения комбинаций сигналов является:

${\text{RMS}}_{\text{AC+DC}}={\sqrt {{\text{V}}_{\text{DC}}^{2}+{\text{RMS}}_{\text{AC}}^{2}}}$

где ${\text{V}}_{\text{DC}}$ относится к компоненту постоянного тока (или среднему значению) сигнала, а ${\text{RMS}}_{\text{AC}}$ — составляющая переменного тока сигнала.

Средняя электрическая мощность

Дополнительная информация: мощность переменного тока.

электрикам часто необходимо знать мощность P R. рассеиваемую сопротивлением электрическим , Инженерам - Легко выполнить расчет, когда постоянный ток протекает I. через сопротивление Для нагрузки сопротивлением Ом мощность определяется по формуле:

$P=I^{2}R.$

Однако, если ток является изменяющейся во времени функцией I ( t ), эту формулу необходимо расширить, чтобы отразить тот факт, что ток (и, следовательно, мгновенная мощность) меняется со временем. Если функция является периодической (например, бытовая мощность переменного тока), все равно имеет смысл обсудить среднюю мощность, рассеиваемую с течением времени, которая рассчитывается путем расчета средней рассеиваемой мощности:

${\begin{aligned}P_{Avg}&=\left(I(t)^{2}R\right)_{Avg}&&{\text{where }}\left(\cdots \right)_{Avg}{\text{ denotes the temporal mean of a function}}\\[3pt]&=\left(I(t)^{2}\right)_{Avg}R&&{\text{(as }}R{\text{ does not vary over time, it can be factored out)}}\\[3pt]&=I_{\text{RMS}}^{2}R&&{\text{by definition of root-mean-square}}\end{aligned}}$

Таким образом, среднеквадратичное значение I _RMS функции I ( t ) представляет собой постоянный ток, который дает ту же рассеиваемую мощность, что и усредненная по времени рассеиваемая мощность тока I ( t ).

что и в случае изменяющегося во времени напряжения Среднюю мощность также можно найти тем же методом , V ( t ) со среднеквадратичным значением V _RMS ,

$P_{\text{Avg}}={V_{\text{RMS}}^{2} \over R}.$

Это уравнение можно использовать для любой периодической формы сигнала , например, синусоидальной или пилообразной , что позволяет нам рассчитать среднюю мощность, подаваемую на указанную нагрузку.

Если извлечь квадратный корень из обоих этих уравнений и умножить их вместе, получим мощность:

$P_{\text{Avg}}=V_{\text{RMS}}I_{\text{RMS}}.$

Оба вывода зависят от пропорциональности напряжения и тока (т. е. нагрузка R является чисто резистивной). Реактивные нагрузки (то есть нагрузки, способные не просто рассеивать энергию, но и хранить ее) обсуждаются в теме мощности переменного тока .

В обычном случае переменного тока , когда I ( t ) является синусоидальным током, что приблизительно верно для мощности сети, среднеквадратичное значение легко вычислить из уравнения непрерывного случая, приведенного выше. Если I _p определяется как пиковый ток, то:

$I_{\text{RMS}}={\sqrt {{1 \over {T_{2}-T_{1}}}\int _{T_{1}}^{T_{2}}\left[I_{\text{p}}\sin(\omega t)\right]^{2}dt}},$

где t — время, а ω — угловая частота ( ω = 2 π / T , где T — период волны).

Поскольку I _p — положительная константа и ее нужно было возвести в квадрат внутри интеграла:

$I_{\text{RMS}}=I_{\text{p}}{\sqrt {{1 \over {T_{2}-T_{1}}}{\int _{T_{1}}^{T_{2}}{\sin ^{2}(\omega t)}\,dt}}}.$

Использование тригонометрического тождества для устранения возведения в квадрат тригонометрической функции:

${\begin{aligned}I_{\text{RMS}}&=I_{\text{p}}{\sqrt {{1 \over {T_{2}-T_{1}}}{\int _{T_{1}}^{T_{2}}{1-\cos(2\omega t) \over 2}\,dt}}}\\[3pt]&=I_{\text{p}}{\sqrt {{1 \over {T_{2}-T_{1}}}\left[{t \over 2}-{\sin(2\omega t) \over 4\omega }\right]_{T_{1}}^{T_{2}}}}\end{aligned}}$

но поскольку интервал представляет собой целое число полных циклов (согласно определению RMS), синусоидальные члены сокращаются, оставляя:

$I_{\text{RMS}}=I_{\text{p}}{\sqrt {{1 \over {T_{2}-T_{1}}}\left[{t \over 2}\right]_{T_{1}}^{T_{2}}}}=I_{\text{p}}{\sqrt {{1 \over {T_{2}-T_{1}}}{{T_{2}-T_{1}} \over 2}}}={I_{\text{p}} \over {\sqrt {2}}}.$

Подобный анализ приводит к аналогичному уравнению для синусоидального напряжения:

$V_{\text{RMS}}={V_{\text{p}} \over {\sqrt {2}}},$

где I _P представляет собой пиковый ток, а V _P представляет собой пиковое напряжение.

Из-за своей полезности при расчете мощности указанные напряжения для розеток (например, 120   В в США или 230   В в Европе) почти всегда указываются в среднеквадратичных, а не пиковых значениях. Пиковые значения можно рассчитать по среднеквадратичным значениям по приведенной выше формуле, из которой следует, что V _P = V _RMS × √ 2 , предполагая, что источником является чистая синусоидальная волна. Таким образом, пиковое значение сетевого напряжения в США составляет около 120 × √ 2 , или около 170 вольт. Пиковое напряжение, вдвое большее, составляет около 340 вольт. Аналогичный расчет показывает, что пиковое сетевое напряжение в Европе составляет около 325 вольт, а размах сетевого напряжения — около 650 вольт.

Среднеквадратические величины, такие как электрический ток, обычно рассчитываются за один цикл. Однако в некоторых целях при расчете потерь мощности передачи требуется среднеквадратичный ток за более длительный период. Применяется тот же принцип, и (например) ток в 10 А, используемый в течение 12 часов каждые 24 часа в сутки, представляет собой средний ток в 5 А, но среднеквадратичный ток составляет 7,07 А в долгосрочной перспективе.

Термин среднеквадратическая мощность иногда ошибочно используется (например, в аудиоиндустрии) как синоним средней мощности или средней мощности (она пропорциональна квадрату среднеквадратичного напряжения или среднеквадратичного тока в резистивной нагрузке). Обсуждение измерений мощности звука и их недостатков см. в разделе Мощность звука .

Скорость

Основная статья: Среднеквадратическая скорость

В физике молекул газа среднеквадратическая скорость определяется как квадратный корень из среднего квадрата скорости. Среднеквадратическая скорость идеального газа рассчитывается по следующему уравнению:

$v_{\text{RMS}}={\sqrt {3RT \over M}}$

где R представляет собой газовую постоянную , 8,314 Дж/(моль·К), T — температура газа в кельвинах , а M — молярная масса газа в килограммах на моль. В физике скорость определяется как скалярная величина скорости. Для неподвижного газа средняя скорость его молекул может составлять порядка тысяч км/ч, хотя средняя скорость его молекул равна нулю.

Ошибка

Основная статья: Среднеквадратичное отклонение

При сравнении двух наборов данных — например, одного из теоретического прогноза, а другого — из фактического измерения какой-либо физической переменной, среднеквадратичное значение парных разностей двух наборов данных может служить мерой того, насколько далеко в среднем находится ошибка. от 0. Среднее значение абсолютных значений парных различий может быть полезной мерой изменчивости различий. Однако среднеквадратическое отклонение различий обычно является предпочтительной мерой, вероятно, из-за математической условности и совместимости с другими формулами.

В частотной области

Среднеквадратичное значение можно вычислить в частотной области, используя теорему Парсеваля . Для дискретизированного сигнала $x[n]=x(t=nT)$, где $T$ период выборки,

$\sum _{n=1}^{N}{x^{2}[n]}={\frac {1}{N}}\sum _{m=1}^{N}\left|X[m]\right|^{2},$

где $X[m]=\operatorname {DFT} \{x[n]\}$ N — размер выборки, то есть количество наблюдений в выборке и коэффициенты ДПФ.

В этом случае среднеквадратичное значение, вычисленное во временной области, такое же, как и в частотной области:

${\text{RMS}}\{x[n]\}={\sqrt {{\frac {1}{N}}\sum _{n}{x^{2}[n]}}}={\sqrt {{\frac {1}{N^{2}}}\sum _{m}{{\bigl |}X[m]{\bigr |}}^{2}}}={\sqrt {\sum _{m}{\left|{\frac {X[m]}{N}}\right|^{2}}}}.$

Связь с другой статистикой

См. также: Точность

Геометрическое доказательство без слов , что max ( a , b ) > среднеквадратичное ( RMS ) или среднее квадратичное ( QM ) > среднее арифметическое ( AM ) > среднее геометрическое ( GM ) > гармоническое ( HM ) > min ( a , b ) среднее два различных положительных числа a и b

Если ${\bar {x}}$ среднее арифметическое и $\sigma _{x}$ — стандартное отклонение совокупности или формы волны , тогда:

$x_{\text{rms}}^{2}={\overline {x}}^{2}+\sigma _{x}^{2}={\overline {x^{2}}}.$

Отсюда ясно, что среднеквадратичное значение всегда больше или равно среднему, поскольку среднеквадратичное значение также включает в себя «ошибку»/квадратичное отклонение.

Учёные-физики часто используют термин «среднеквадратичное» как синоним стандартного отклонения , когда можно предположить, что входной сигнал имеет нулевое среднее, то есть относится к квадратному корню из среднеквадратического отклонения сигнала от заданной базовой линии или подгонки. Это полезно инженерам-электрикам при расчете среднеквадратического значения сигнала «только переменный ток». Стандартное отклонение, представляющее собой среднеквадратичное отклонение сигнала относительно среднего значения, а не около 0, компонент постоянного тока удаляется (т. е. среднеквадратичное отклонение (сигнал) = стандартное отклонение (сигнал), если среднее значение сигнала равно 0).

См. также

• Пифагорово сложение
• Среднее исправленное значение (ARV)
• Центральный момент
• Среднее геометрическое
• L2 норма
• Наименьшие квадраты
• Словарь математических символов
• Среднеквадратичное смещение
• Конвертер реальных среднеквадратичных значений

Внешние ссылки

• Объяснение того, почему RMS является неправильным термином применительно к мощности звука.
• Java-апплет для изучения RMS