Последовательность пальцев

Диаграмма Фарея к F ₉ .

Симметричный узор, составленный знаменателями последовательности Фэрея F ₉ .

Симметричный узор, составленный знаменателями последовательности Фэрея, F ₂₅ .

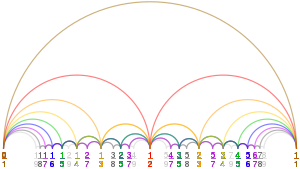
В математике последовательность Фарея порядка n — это последовательность полностью уменьшенных дробей либо между 0 и 1, либо без этого ограничения, ^{[ а ]} которые в наименьших терминах имеют знаменатели, меньшие или равные n , расположенные в порядке возрастания размера.

При ограниченном определении каждая последовательность Фарея начинается со значения 0, обозначаемого дробью ⁠ 0/1 и ⁠ заканчивается значением 1, обозначаемым дробью ⁠ 1/1 авторы опускают эти (хотя некоторые ⁠ термины).

Последовательность Фарея иногда называют рядом Фарея , что не совсем правильно, поскольку члены не суммируются. ^{[ 2 ]}

Примеры

Последовательности Фарея порядков с 1 по 8:

Ф ₁ = { ⁠ 0 1 ⁠ _, ⁠ 1 1 ⁠ }

F2 _{ = ⁠ 0 1 ⁠ _, ⁠ 1 2 ⁠ _, ⁠ 1 1 ⁠ }

F ₃ = { ⁠ 0 1 ⁠ _, ⁠ 1 3 ⁠ _, ⁠ 1 2 ⁠ _, ⁠ 2 3 ⁠ _, ⁠ 1 1 ⁠ }

Ф ₄ = { ⁠ 0 1 ⁠ _, ⁠ 1 4 ⁠ _, ⁠ 1 3 ⁠ _, ⁠ 1 2 ⁠ _, ⁠ 2 3 ⁠ _, ⁠ 3 4 ⁠ _, ⁠ 1 1 ⁠ }

Ф ₅ = { ⁠ 0 1 ⁠ _, ⁠ 1 5 ⁠ _, ⁠ 1 4 ⁠ _, ⁠ 1 3 ⁠ _, ⁠ 2 5 ⁠ _, ⁠ 1 2 ⁠ _, ⁠ 3 5 ⁠ _, ⁠ 2 3 ⁠ _, ⁠ 3 4 ⁠ _, ⁠ 4 5 ⁠ _, ⁠ 1 1 ⁠ }

Ф ₆ = { ⁠ 0 1 ⁠ _, ⁠ 1 6 ⁠ _, ⁠ 1 5 ⁠ _, ⁠ 1 4 ⁠ _, ⁠ 1 3 ⁠ _, ⁠ 2 5 ⁠ _, ⁠ 1 2 ⁠ _, ⁠ 3 5 ⁠ _, ⁠ 2 3 ⁠ _, ⁠ 3 4 ⁠ _, ⁠ 4 5 ⁠ _, ⁠ 5 6 ⁠ _, ⁠ 1 1 ⁠ }

Ф ₇ = { ⁠ 0 1 ⁠ _, ⁠ 1 7 ⁠ _, ⁠ 1 6 ⁠ _, ⁠ 1 5 ⁠ _, ⁠ 1 4 ⁠ _, ⁠ 2 7 ⁠ _, ⁠ 1 3 ⁠ _, ⁠ 2 5 ⁠ _, ⁠ 3 7 ⁠ _, ⁠ 1 2 ⁠ _, ⁠ 4 7 ⁠ _, ⁠ 3 5 ⁠ _, ⁠ 2 3 ⁠ _, ⁠ 5 7 ⁠ _, ⁠ 3 4 ⁠ _, ⁠ 4 5 ⁠ _, ⁠ 5 6 ⁠ _, ⁠ 6 7 ⁠ _, ⁠ 1 1 ⁠ }

Ф ₈ = { ⁠ 0 1 ⁠ _, ⁠ 1 8 ⁠ _, ⁠ 1 7 ⁠ _, ⁠ 1 6 ⁠ _, ⁠ 1 5 ⁠ _, ⁠ 1 4 ⁠ _, ⁠ 2 7 ⁠ _, ⁠ 1 3 ⁠ _, ⁠ 3 8 ⁠ _, ⁠ 2 5 ⁠ _, ⁠ 3 7 ⁠ _, ⁠ 1 2 ⁠ _, ⁠ 4 7 ⁠ _, ⁠ 3 5 ⁠ _, ⁠ 5 8 ⁠ _, ⁠ 2 3 ⁠ _, ⁠ 5 7 ⁠ _, ⁠ 3 4 ⁠ _, ⁠ 4 5 ⁠ _, ⁠ 5 6 ⁠ _, ⁠ 6 7 ⁠ _, ⁠ 7 8 ⁠ _, ⁠ 1 1 ⁠ }

Центрировано
Ф ₁ = { ⁠ 0 / 1 ⁠ _, ⁠ 1 / 1 ⁠ }
F2 _{ = ⁠ 0 / 1 ⁠ _, ⁠ 1 / 2 ⁠ _, ⁠ 1 / 1 ⁠ }
F ₃ = { ⁠ 0 / 1 ⁠ _, ⁠ 1 / 3 ⁠ _, ⁠ 1 / 2 ⁠ _, ⁠ 2 / 3 ⁠ _, ⁠ 1 / 1 ⁠ }
Ф ₄ = { ⁠ 0 / 1 ⁠ _, ⁠ 1 / 4 ⁠ _, ⁠ 1 / 3 ⁠ _, ⁠ 1 / 2 ⁠ _, ⁠ 2 / 3 ⁠ _, ⁠ 3 / 4 ⁠ _, ⁠ 1 / 1 ⁠ }
Ф ₅ = { ⁠ 0 / 1 ⁠ _, ⁠ 1 / 5 ⁠ _, ⁠ 1 / 4 ⁠ _, ⁠ 1 / 3 ⁠ _, ⁠ 2 / 5 ⁠ _, ⁠ 1 / 2 ⁠ _, ⁠ 3 / 5 ⁠ _, ⁠ 2 / 3 ⁠ _, ⁠ 3 / 4 ⁠ _, ⁠ 4 / 5 ⁠ _, ⁠ 1 / 1 ⁠ }
Ф ₆ = { ⁠ 0 / 1 ⁠ _, ⁠ 1 / 6 ⁠ _, ⁠ 1 / 5 ⁠ _, ⁠ 1 / 4 ⁠ _, ⁠ 1 / 3 ⁠ _, ⁠ 2 / 5 ⁠ _, ⁠ 1 / 2 ⁠ _, ⁠ 3 / 5 ⁠ _, ⁠ 2 / 3 ⁠ _, ⁠ 3 / 4 ⁠ _, ⁠ 4 / 5 ⁠ _, ⁠ 5 / 6 ⁠ _, ⁠ 1 / 1 ⁠ }
Ф ₇ = { ⁠ 0 / 1 ⁠ _, ⁠ 1 / 7 ⁠ _, ⁠ 1 / 6 ⁠ _, ⁠ 1 / 5 ⁠ _, ⁠ 1 / 4 ⁠ _, ⁠ 2 / 7 ⁠ _, ⁠ 1 / 3 ⁠ _, ⁠ 2 / 5 ⁠ _, ⁠ 3 / 7 ⁠ _, ⁠ 1 / 2 ⁠ _, ⁠ 4 / 7 ⁠ _, ⁠ 3 / 5 ⁠ _, ⁠ 2 / 3 ⁠ _, ⁠ 5 / 7 ⁠ _, ⁠ 3 / 4 ⁠ _, ⁠ 4 / 5 ⁠ _, ⁠ 5 / 6 ⁠ _, ⁠ 6 / 7 ⁠ _, ⁠ 1 / 1 ⁠ }
Ф ₈ = { ⁠ 0 / 1 ⁠ _, ⁠ 1 / 8 ⁠ _, ⁠ 1 / 7 ⁠ _, ⁠ 1 / 6 ⁠ _, ⁠ 1 / 5 ⁠ _, ⁠ 1 / 4 ⁠ _, ⁠ 2 / 7 ⁠ _, ⁠ 1 / 3 ⁠ _, ⁠ 3 / 8 ⁠ _, ⁠ 2 / 5 ⁠ _, ⁠ 3 / 7 ⁠ _, ⁠ 1 / 2 ⁠ _, ⁠ 4 / 7 ⁠ _, ⁠ 3 / 5 ⁠ _, ⁠ 5 / 8 ⁠ _, ⁠ 2 / 3 ⁠ _, ⁠ 5 / 7 ⁠ _, ⁠ 3 / 4 ⁠ _, ⁠ 4 / 5 ⁠ _, ⁠ 5 / 6 ⁠ _, ⁠ 6 / 7 ⁠ _, ⁠ 7 / 8 ⁠ _, ⁠ 1 / 1 ⁠ }

Отсортировано

 F1 = {0/1,                                                                                                          1/1}
 F2 = {0/1,                                                   1/2,                                                   1/1}
 F3 = {0/1,                               1/3,                1/2,                2/3,                               1/1}
 F4 = {0/1,                     1/4,      1/3,                1/2,                2/3,      3/4,                     1/1}
 F5 = {0/1,                1/5, 1/4,      1/3,      2/5,      1/2,      3/5,      2/3,      3/4, 4/5,                1/1}
 F6 = {0/1,           1/6, 1/5, 1/4,      1/3,      2/5,      1/2,      3/5,      2/3,      3/4, 4/5, 5/6,           1/1}
 F7 = {0/1,      1/7, 1/6, 1/5, 1/4, 2/7, 1/3,      2/5, 3/7, 1/2, 4/7, 3/5,      2/3, 5/7, 3/4, 4/5, 5/6, 6/7,      1/1}
 F8 = {0/1, 1/8, 1/7, 1/6, 1/5, 1/4, 2/7, 1/3, 3/8, 2/5, 3/7, 1/2, 4/7, 3/5, 5/8, 2/3, 5/7, 3/4, 4/5, 5/6, 6/7, 7/8, 1/1}

Фейри Санберст

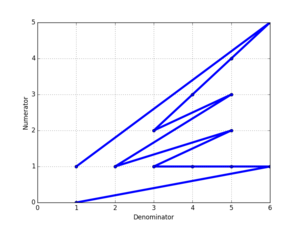
Построение графика зависимости числителей от знаменателей последовательности Фарея дает форму, подобную той, что справа, показанной для $F 6 .$

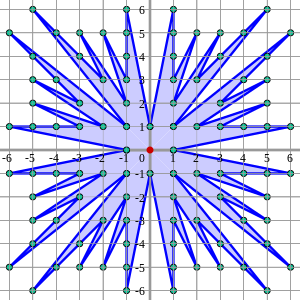
Отражение этой формы вокруг диагональной и главной осей создает солнечные лучи Фейри , показанные ниже. Солнечная вспышка Фарея порядка $n$ соединяет видимые точки целочисленной сетки от начала координат в квадрате со стороной $2 n$ с центром в начале координат. Используя теорему Пика , площадь солнечной вспышки равна $4(| F n | - 1)$ , где $| ж п |$ — количество дробей в $F n$ .

История

Очень любопытна история «сериала Фэри» — Харди и Райт (1979). ^{[ 3 ]}

... И снова человек, чье имя было дано математическому соотношению, не был первооткрывателем, насколько свидетельствуют записи. - Бейлер (1964) ^{[ 4 ]}

Последовательности Фейри названы в честь британского геолога Джона Фейри-старшего , чье письмо об этих последовательностях было опубликовано в «Философском журнале» в 1816 году. Фейри предположил, не предоставив доказательств, что каждый новый член в разложении последовательности Фэрея является медиантой своих соседей. . Письмо Фарея было прочитано Коши , который представил доказательство в своих математических упражнениях и приписал этот результат Фарею. Фактически, другой математик, Чарльз Арос , опубликовал аналогичные результаты в 1802 году, которые не были известны ни Фари, ни Коши. ^{[ 4 ]} Таким образом, это была историческая случайность, которая связала имя Фари с этими эпизодами. Это пример закона эпонимии Стиглера .

Характеристики

Длина последовательности и индекс дроби

Последовательность Фарея порядка n содержит все члены последовательностей Фарея более низких порядков. В частности, F _n содержит все члены F _{n −1} , а также содержит дополнительную дробь для каждого числа, которое меньше n и взаимно просто с n . Таким образом, F ₆ состоит из F ₅ вместе с дробями ⁠ 1/6 ⁠ и ⁠ 5 / 6 ⁠ .

Средний член последовательности Фарея F _n всегда равен ⁠ 1/2 ⁠ , для n > 1. Отсюда мы можем связать длины F _n и F _{n −1,} используя функцию тотента Эйлера $\varphi (n)$ :

|F_{n}|=|F_{n-1}|+\varphi (n).

Используя тот факт, что | Ф ₁ | = 2, мы можем вывести выражение для длины F _n : ^{[ 5 ]}

|F_{n}|=1+\sum _{m=1}^{n}\varphi (m)=1+\Phi (n),

где $\Phi (n)$ является суммирующим фактором .

У нас также есть:

|F_{n}|={\frac {1}{2}}\left(3+\sum _{d=1}^{n}\mu (d)\left\lfloor {\tfrac {n}{d}}\right\rfloor ^{2}\right),

и по формуле обращения Мёбиуса :

|F_{n}|={\frac {1}{2}}(n+3)n-\sum _{d=2}^{n}|F_{\lfloor n/d\rfloor }|,

где $µ(d)$ — теоретико-числовая функция Мёбиуса , и $\lfloor {\tfrac {n}{d}}\rfloor$ это функция пола .

Асимптотическое поведение | ж _п | является :

|F_{n}|\sim {\frac {3n^{2}}{\pi ^{2}}}.

Количество дробей Фарея со знаменателями, равными $k$ в F _n определяется выражением $\varphi (k)$ когда $k\leq n$ и ноль в противном случае. Относительно числителей можно определить функцию ${\mathcal {N}}_{n}(h)$ который возвращает количество дробей Фарея с числителями, равными $h$ в Фн _. Эта функция имеет несколько интересных свойств: ^{[ 6 ]}

{\mathcal {N}}_{n}(1)=n

,

{\mathcal {N}}_{n}(p^{m})=\left\lceil (n-p^{m})\left(1-1/p\right)\right\rceil

для любого простого числа

p

,

{\mathcal {N}}_{n+mh}(h)={\mathcal {N}}_{n}(h)+m\varphi (h)

для любого целого числа

m\geq 0

,

{\mathcal {N}}_{n}(4h)={\mathcal {N}}_{n}(2h)-\varphi (2h)

.

В частности, свойство в третьей строке выше подразумевает ${\mathcal {N}}_{mh}(h)=(m-1)\varphi (h)$ и, далее, ${\mathcal {N}}_{2h}(h)=\varphi (h)$ . Последнее означает, что для последовательностей Фарея четного порядка n количество дробей с числителями, равными n/2 , совпадает с количеством дробей со знаменателями, равными n/2 , т.е. ${\mathcal {N}}_{n}(n/2)=\varphi (n/2)$ .

Индекс $I_{n}(a_{k,n})=k$ дроби $a_{k,n}$ в последовательности Фэрея $F_{n}=\{a_{k,n}:k=0,1,\ldots ,m_{n}\}$ это просто позиция, которая $a_{k,n}$ занимает в последовательности. Это имеет особое значение, поскольку используется в альтернативной формулировке гипотезы Римана , см. ниже . Далее следуют различные полезные свойства:

I_{n}(0/1)=0,

I_{n}(1/n)=1,

I_{n}(1/2)=(|F_{n}|-1)/2,

I_{n}(1/1)=|F_{n}|-1,

I_{n}(h/k)=|F_{n}|-1-I_{n}((k-h)/k).

Индекс $1/k$ где $n/(i+1)<k\leq n/i$ и $n$ является наименьшим общим кратным первого $i$ цифры, $n={\rm {lcm}}([2,i])$ , определяется: ^{[ 7 ]}

I_{n}(1/k)=1+n\sum _{j=1}^{i}{\frac {\varphi (j)}{j}}-k\Phi (i).

Соседи Фари

Дроби, являющиеся соседними членами в любой последовательности Фарея, называются парой Фарея и обладают следующими свойствами.

Если ⁠ а / б ⁠ и ⁠ c / d ⁠ являются соседями в последовательности Фарея, причем $⁠ а / б ⁠ < ⁠ c / d ⁠$ , то их разница $⁠ c / d ⁠ - ⁠ a / b ⁠$ равно ⁠ 1 / сп ⁠ . С

{\frac {c}{d}}-{\frac {a}{b}}={\frac {bc-ad}{bd}},

это равносильно тому, что

bc-ad=1

.

Таким образом ⁠ 1/3 ⁠ и ⁠ 2/5 , и их ⁠ — соседи в F ₅ разница равна ⁠ 1 / 15 ⁠ .

Обратное также верно. Если

bc-ad=1

для натуральных чисел a , b , c и d с a < b и c < d, тогда ⁠ а / б ⁠ и ⁠ c / d ⁠ будут соседями в последовательности Фарея порядка max( b,d ).

Если ⁠ p / q ⁠ имеет соседей ⁠ а / б ⁠ и ⁠ c / d ⁠ в некоторой последовательности Фарея, где

{\frac {a}{b}}<{\frac {p}{q}}<{\frac {c}{d}}

затем ⁠ p / q ⁠ — медиата ⁠ а / б ⁠ и ⁠ c / d ⁠ – другими словами,

{\frac {p}{q}}={\frac {a+c}{b+d}}.

Это легко следует из предыдущего свойства, поскольку если $bp - aq = qc - pd = 1$ , то $bp + pd = qc + aq$ , $p (b + d) = q (a + c)$ , $⁠ p / q ⁠ = ⁠ а + c / б + d ⁠$ .

Отсюда следует, что если ⁠ а / б ⁠ и ⁠ c / d ⁠ являются соседями в последовательности Фарея, то первый член, который появляется между ними при увеличении порядка последовательности Фари, равен

{\frac {a+c}{b+d}},

который впервые появляется в последовательности Фарея порядка $b + d$ .

Таким образом, первый член, который появляется между ⁠ 1/3 ⁠ и ⁠ 2 / 5 ⁠ это ⁠ 3/8 , 8 ⁠ в F _. который появляется

Общее количество пар соседей Фарея в F _n равно 2| ж _п | − 3.

Дерево Штерна-Броко — это структура данных, показывающая, как строится последовательность, начиная с 0 ( = ⁠ 0 / 1 ⁠ ) и 1 ( = ⁠ 1 / 1 ⁠ ) , взяв последовательные медианы.

Интерпретация эквивалентной площади

Каждая последовательная пара рациональных чисел Фэрея имеет эквивалентную площадь, равную 1. ^{[ 8 ]} Убедитесь в этом, интерпретируя последовательные рациональные числа r ₁ = p / q и r ₂ = p ′/ q ′ как векторы ( p , q ) в плоскости x – y. Площадь A ( p / q , p ′/ q ′) определяется выражением qp ′ − q ′ p . Поскольку любая добавленная дробь между двумя предыдущими последовательными дробями последовательности Фарея рассчитывается как медиана (⊕), тогда A ( r ₁ , r ₁ ⊕ r ₂ ) = A ( r ₁ , r ₁ ) + A ( r ₁ , r ₂ ) = A ( r ₁ , r ₂ ) = 1 (поскольку r ₁ = 1/0 и r ₂ = 0/1, его площадь должна быть равна 1).

Соседи Фари и продолженные дроби

Дроби, которые появляются как соседи в последовательности Фарея, имеют тесно связанные разложения непрерывных дробей . Каждая дробь имеет два разложения непрерывных дробей — в одном последний член равен 1; в другом конечном члене больше на 1. Если ⁠ p / q ⁠ , который впервые появляется в последовательности Фарея F _q , имеет разложение в непрерывную дробь.

[0; а ₁ , а ₂ , ..., а _{п - 1} , а _п , 1]

[0; а ₁ , а ₂ , ..., а _{п - 1} , а _п + 1]

тогда ближайший сосед ⁠ p / q ⁠ в F _q (который будет его соседом с большим знаменателем) имеет разложение в цепную дробь

[0; а ₁ , а ₂ , ... н _, ]

а другой его сосед имеет непрерывное дробное расширение

[0; а ₁ , а ₂ , ..., а _{п - 1} ]

Например, ⁠ 3 / 8 ⁠ имеет два разложения цепной дроби [0; 2, 1, 1, 1] и [0; 2, 1, 2] , а его соседями в F ₈ являются ⁠ 2 / 5 ⁠ , который можно расширить как [0; 2, 1, 1] ; и ⁠ 1 / 3 ⁠ , который можно расширить как [0; 2, 1] .

Дроби Фарея и наименьшее общее кратное

lcm можно выразить как произведение фракций Фарея как

{\text{lcm}}[1,2,...,N]=e^{\psi (N)}={\frac {1}{2}}\left(\prod _{r\in F_{N},0<r\leq 1/2}2\sin(\pi r)\right)^{2}

где $\psi (N)$ – вторая функция Чебышева . ^{[ 9 ]}^{[ 10 ]}

Дроби Фарея и наибольший общий делитель

Поскольку функция тотента Эйлера напрямую связана с НОД, то же самое относится и к количеству элементов в F _n ,

|F_{n}|=1+\sum _{m=1}^{n}\varphi (m)=1+\sum \limits _{m=1}^{n}\sum \limits _{k=1}^{m}\gcd(k,m)\cos {2\pi {\frac {k}{m}}}.

Для любых 3 фракций Фарея ⁠ a / b ⁠ , ⁠ с / д ⁠ и ⁠ e / f ⁠ имеет место следующее тождество между НОД 2x2 определителей матрицы по абсолютной величине: ^{[ 11 ]}

\gcd \left({\begin{Vmatrix}a&c\\b&d\end{Vmatrix}},{\begin{Vmatrix}a&e\\b&f\end{Vmatrix}}\right)=\gcd \left({\begin{Vmatrix}a&c\\b&d\end{Vmatrix}},{\begin{Vmatrix}c&e\\d&f\end{Vmatrix}}\right)=\gcd \left({\begin{Vmatrix}a&e\\b&f\end{Vmatrix}},{\begin{Vmatrix}c&e\\d&f\end{Vmatrix}}\right)

^{[ 7 ]}

Приложения

Последовательности Фарея очень полезны для поиска рациональных приближений иррациональных чисел. ^{[ 12 ]} Например, конструкция Элиаху ^{[ 13 ]} Чтобы получить нижнюю границу длины нетривиальных циклов в процессе 3 x +1, используются последовательности Фарея для вычисления разложения числа log ₂ в непрерывную дробь (3).

В физических системах с резонансными явлениями последовательности Фарея представляют собой очень элегантный и эффективный метод расчета местоположений резонансов в 1D. ^{[ 14 ]} и 2Д. ^{[ 15 ]}

Последовательности Фарея играют важную роль в исследованиях планирования пути под любым углом на сетках с квадратными ячейками, например, для характеристики их вычислительной сложности. ^{[ 16 ]} или оптимальность. ^{[ 17 ]} Соединение можно рассматривать с точки зрения r -ограниченных путей, а именно путей, состоящих из отрезков линий, каждый из которых пересекает не более $r$ ряды и максимум $r$ столбцы ячеек. Позволять $Q$ быть набором векторов $(q,p)$ такой, что $1\leq q\leq r$ , $0\leq p\leq q$ , и $p$ , $q$ взаимнопросты. Позволять $Q*$ быть результатом размышления $Q$ в линии $y=x$ . Позволять $S=\{(\pm x,\pm y):(x,y)\in Q\cup Q*\}$ . Тогда любой путь с r -ограничениями можно описать как последовательность векторов из $S$ . Существует биекция между $Q$ и последовательность порядка Фарея $r$ данный $(q,p)$ сопоставление с ${\tfrac {p}{q}}$ .

Фордовые круги

Существует связь между последовательностью Фэрея и кругами Форда .

Для каждой дроби ⁠ p / q ⁠ (в низших терминах) существует круг Форда C[ ⁠ p / q ⁠ ], представляющий собой круг радиуса 1/(2 q ²) и центр в ( ⁠ p / q ⁠ , ⁠ 1/2 кв . ² ⁠ ). Два круга Форда для разных дробей либо не пересекаются , либо касаются друг друга — два круга Форда никогда не пересекаются. Если 0 < ⁠ p / q ⁠ < 1, то окружности Форда, касающиеся C[ ⁠ p / q ⁠ ] — это в точности круги Форда для дробей, являющихся соседями ⁠ p / q ⁠ в некоторой последовательности Фарея.

Таким образом, C [ ⁠ 2 / 5 ⁠ ] касается C [ ⁠ 1 / 2 ⁠ ], C [ ⁠ 1 / 3 ⁠ ], C [ ⁠ 3 / 7 ⁠ ], C [ ⁠ 3/8 . ⁠ ] и т. д

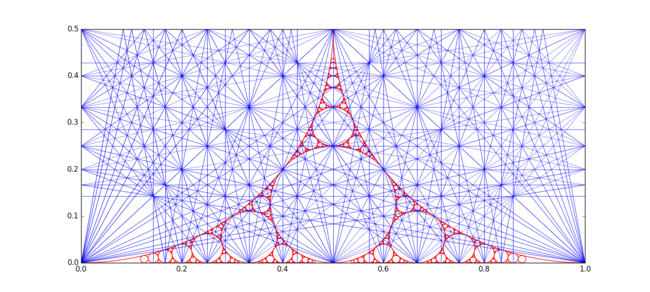
Круги Форда появляются и в аполлонической прокладке (0,0,1,1). На рисунке ниже это показано вместе с резонансными линиями Фарея. ^{[ 18 ]}

Гипотеза Римана

Последовательности Фарея используются в двух эквивалентных формулировках гипотезы Римана . Предположим, условия $F_{n}$ являются $\{a_{k,n}:k=0,1,\ldots ,m_{n}\}$ . Определять $d_{k,n}=a_{k,n}-k/m_{n}$ , другими словами $d_{k,n}$ - это разница между k -м членом n-й последовательности Фарея и k -м членом набора из того же количества точек, равномерно распределенных на единичном интервале. В 1924 году Жером Франель. ^{[ 19 ]} доказал, что утверждение

\sum _{k=1}^{m_{n}}d_{k,n}^{2}=O(n^{r})\quad \forall r>-1

эквивалентно гипотезе Римана, а затем Эдмунда Ландау ^{[ 20 ]} заметил (сразу после статьи Франеля), что утверждение

\sum _{k=1}^{m_{n}}|d_{k,n}|=O(n^{r})\quad \forall r>1/2

также эквивалентно гипотезе Римана.

Другие суммы, включающие дроби Фарея

Сумма всех дробей Фарея порядка n равна половине количества элементов:

\sum _{r\in F_{n}}r={\frac {1}{2}}|F_{n}|.

Сумма знаменателей в последовательности Фарея в два раза превышает сумму числителей и относится к общей функции Эйлера:

\sum _{a/b\in F_{n}}b=2\sum _{a/b\in F_{n}}a=1+\sum _{i=1}^{n}i\varphi (i),

которое было предположено Гарольдом Л. Аароном в 1962 году и продемонстрировано Джин А. Блейк в 1966 году. ^{[ 21 ]} Однострочное доказательство гипотезы Гарольда Л. Аарона выглядит следующим образом. Сумма числителей равна ${\displaystyle 1+\sum _{2\leq b\leq n}\sum _{(a,b)=1}a=1+\sum _{2\leq b\leq n}b{\frac {\varphi (b)}{2}}}$ . Сумма знаменателей равна ${\displaystyle 2+\sum _{2\leq b\leq n}\sum _{(a,b)=1}b=2+\sum _{2\leq b\leq n}b\varphi (b)}$ . Частное первой суммы на вторую сумму равно ${\frac {1}{2}}$ .

Пусть b _j — упорядоченные знаменатели F _n , тогда: ^{[ 22 ]}

\sum _{j=0}^{|F_{n}|-1}{\frac {b_{j}}{b_{j+1}}}={\frac {3|F_{n}|-4}{2}}

и

\sum _{j=0}^{|F_{n}|-1}{\frac {1}{b_{j+1}b_{j}}}=1.

Пусть a _j / b _{j —} -я дробь j Фарея в F _n , тогда

\sum _{j=1}^{|F_{n}|-1}(a_{j-1}b_{j+1}-a_{j+1}b_{j-1})=\sum _{j=1}^{|F_{n}|-1}{\begin{Vmatrix}a_{j-1}&a_{j+1}\\b_{j-1}&b_{j+1}\end{Vmatrix}}=3(|F_{n}|-1)-2n-1,

что продемонстрировано в. ^{[ 23 ]} Также согласно этой ссылке член внутри суммы может быть выражен по-разному:

a_{j-1}b_{j+1}-a_{j+1}b_{j-1}={\frac {b_{j-1}+b_{j+1}}{b_{j}}}={\frac {a_{j-1}+a_{j+1}}{a_{j}}}=\left\lfloor {\frac {n+b_{j-1}}{b_{j}}}\right\rfloor ,

получая таким образом много разных сумм по элементам Фарея с одним и тем же результатом. Использование симметрии вокруг 1/2 прежнего сумма может быть ограничена половиной последовательности как

\sum _{j=1}^{\lfloor |F_{n}|/2\rfloor }(a_{j-1}b_{j+1}-a_{j+1}b_{j-1})=3(|F_{n}|-1)/2-n-\lceil n/2\rceil ,

Функцию Мертенса можно выразить в виде суммы по дробям Фарея:

M(n)=-1+\sum _{a\in {\mathcal {F}}_{n}}e^{2\pi ia}

где

{\mathcal {F}}_{n}

— последовательность Фарея порядка n .

Эта формула используется при доказательстве теоремы Франеля–Ландау . ^{[ 24 ]}

Следующий семестр

Существует удивительно простой алгоритм генерации членов F _n либо в традиционном порядке (по возрастанию), либо в нетрадиционном порядке (по убыванию). Алгоритм вычисляет каждую последующую запись на основе двух предыдущих записей, используя указанное выше свойство медианы. Если ⁠ а / б ⁠ и ⁠ c / d ⁠ — две заданные записи, и ⁠ p / q ⁠ — неизвестная следующая запись, тогда $⁠ c / d ⁠ = ⁠ а + п / б + q ⁠$ . С ⁠ c / d ⁠ — это в самых низких терминах, должно существовать целое число k такое, что $kc = a + p$ и $kd = b + q$ , что дает $p = kc - a$ и $q = kd - b$ . Если мы считаем p и q функциями k , то

{\frac {p(k)}{q(k)}}-{\frac {c}{d}}={\frac {cb-da}{d(kd-b)}}

поэтому чем больше k , тем ближе ⁠ p / q ⁠ добирается до ⁠ c / d ⁠ .

Чтобы получить следующий член последовательности, k должно быть как можно большим при условии, что $kd - b \leq n$ (поскольку мы рассматриваем только числа со знаменателями, не превышающими n ), поэтому k — наибольшее целое число ≤ n. ⁠ п + б / д ⁠ . Подводя это значение k обратно в уравнения для p и q, получаем

p=\left\lfloor {\frac {n+b}{d}}\right\rfloor c-a

q=\left\lfloor {\frac {n+b}{d}}\right\rfloor d-b

это реализовано В Python следующим образом:

from fractions import Fraction
from collections.abc import Generator


def farey_sequence(n: int, descending: bool = False) -> Generator[Fraction]:
    """
    Print the n'th Farey sequence. Allow for either ascending or descending.

    >>> print(*farey_sequence(5), sep=' ')
    0 1/5 1/4 1/3 2/5 1/2 3/5 2/3 3/4 4/5 1
    """
    a, b, c, d = 0, 1, 1, n
    if descending:
        a, c = 1, n - 1
    yield Fraction(a, b)
    while 0 <= c <= n:
        k = (n + b) // d
        a, b, c, d = c, d, k * c - a, k * d - b
        yield Fraction(a, b)


if __name__ == "__main__":
    import doctest

    doctest.testmod()

При грубом поиске решений диофантовых уравнений в рациональных числах часто можно воспользоваться рядом Фэрея (для поиска только приведенных форм). Хотя этот код использует первые два термина последовательности для инициализации a , b , c и d , можно заменить любую пару соседних терминов, чтобы исключить те, которые меньше (или больше) определенного порога. ^{[ 25 ]}

См. также

Сноски

^ « Последовательность всех приведенных дробей со знаменателями, не превышающими n, перечисленных в порядке их размера, называется последовательностью Фарея порядка n. С комментарием: « Это определение последовательностей Фарея кажется наиболее удобным. Однако некоторые авторы предпочитают ограничивать дроби интервалом от 0 до 1 ». — Нивен и Цукерман (1972). ^{[ 1 ]}

Ссылки

^ Нивен Иван М. ; Цукерман, Герберт С. (1972). Введение в теорию чисел (Третье изд.). Джон Уайли и сыновья. Определение 6.1.
^ Гутери, Скотт Б. (2011). «1. Медиант» . Мотив математики: история и применение медианы и последовательности Фарея . Бостон: Доцент Пресс. п. 7. ISBN 978-1-4538-1057-6 . OCLC 1031694495 . Проверено 28 сентября 2020 г.
^ Харди, штат Джорджия ; Райт, Э.М. (1979). Введение в теорию чисел (Пятое изд.). Издательство Оксфордского университета. Глава III . ISBN 0-19-853171-0 .
^ Перейти обратно: ^а ^б Бейлер, Альберт Х. (1964). Отдых в теории чисел (второе изд.). Дувр. Глава XVI. ISBN 0-486-21096-0 . Цитируется в «Сериал о Фэйри, история» . Разрезать узел .
^ Слоан, Нью-Джерси (ред.). «Последовательность A005728» . Электронная энциклопедия целочисленных последовательностей . Фонд ОЭИС.
^ Томас Гарсия, Рохелио (июль 2024 г.). «Дроби Фэри с равными числителями и рангом единичных дробей» (PDF) . Целые числа . 24 .
^ Перейти обратно: ^а ^б Томас, Рохелио (январь 2022 г.). «Частичные суммы Франеля» (PDF) . Журнал целочисленных последовательностей . 25 (1).
^ Остин, Дэвид (декабрь 2008 г.). «Деревья, зубы и время: математика изготовления часов» . Американское математическое общество . Род-Айленд. Архивировано из оригинала 4 февраля 2020 года . Проверено 28 сентября 2020 г.
^ Мартин, Грег (2009). «Произведение значений гамма-функции на дроби с одинаковым знаменателем». arXiv : 0907.4384 [ math.CA ].
^ Вемайер, Стефан (2009). «LCM(1,2,...,n) как произведение синусоидальных значений, выбранных по точкам в последовательностях Фарея». arXiv : 0909.1838 [ math.CA ].
^ Томас Гарсия, Рохелио (август 2020 г.). «Равенства между наибольшими общими делителями, включающими три пары взаимно простых чисел» (PDF) . Заметки по теории чисел и дискретной математике . 26 (3): 5–7. дои : 10.7546/nntdm.2020.26.3.5-7 . S2CID 225280271 .
^ «Приближение Фарея» . NRICH.maths.org . Архивировано из оригинала 19 ноября 2018 года . Проверено 18 ноября 2018 г.
^ Элиаху, Шалом (август 1993 г.). «Проблема 3x+1: новые нижние оценки нетривиальных длин циклов» . Дискретная математика . 118 (1–3): 45–56. дои : 10.1016/0012-365X(93)90052-U .
^ Чжэньхуа Ли, А.; Хартер, РГ (2015). «Квантовое возрождение осцилляторов Морса и геометрии Фарея – Форда». хим. Физ. Летт . 633 : 208–213. arXiv : 1308.4470 . Бибкод : 2015CPL...633..208L . дои : 10.1016/j.cplett.2015.05.035 . S2CID 66213897 .
^ Томас, Р. (2014). «От последовательностей Фэрея к резонансным диаграммам» (PDF) . Специальные темы Physical Review — Ускорители и пучки . 17 (1): 014001. Бибкод : 2014PhRvS..17a4001T . doi : 10.1103/PhysRevSTAB.17.014001 .
^ Харабор, Дэниел Дамир; Грастиен, Альбан; Собственный, Религиозный; Аксакалли, Вурал (26 мая 2016 г.). «Оптимальный поиск пути под любым углом на практике» . Журнал исследований искусственного интеллекта . 56 : 89–118. дои : 10.1613/jair.5007 .
^ Хью, Патрик Чисан (19 августа 2017 г.). «Длина кратчайших путей вершин в двоичных сетках занятости по сравнению с кратчайшими r -ограниченными» . Журнал исследований искусственного интеллекта . 59 : 543–563. дои : 10.1613/jair.5442 .
^ Томас, Рохелио (2020). «Недочеты и исправления». arXiv : 2006.10661 [ physical.acc-ph ].
^ Франель, Джером (1924). «Сюиты Фарея и проблема имен премьер» . Новости Общества наук в Геттингене . Математико-физический класс (на французском языке): 198–201.
^ Ландау, Эдмунд (1924). «Замечания к вышеуказанному трактату г-на Франеля» . Новости Общества наук в Геттингене . Математико-физический класс (на немецком языке): 202–206.
^ Блейк, Джин А. (1966). «Некоторые характерные свойства ряда Фарея». Американский математический ежемесячник . 73 (1): 50–52. дои : 10.2307/2313922 . JSTOR 2313922 .
^ Курт Герстмайр; Гистмайр, Курт (2010). «Суммы Фарея и суммы Дедекинда». Американский математический ежемесячник . 117 (1): 72–78. дои : 10.4169/000298910X475005 . JSTOR 10.4169/000298910X475005 . S2CID 31933470 .
^ Холл, РР; Шиу, П. (2003). «Индекс последовательности Фарея» . Мичиганская математика. Дж . 51 (1): 209–223. дои : 10.1307/mmj/1049832901 .
^ Эдвардс, Гарольд М. (1974). «12.2 Сборник. Гипотеза Римана и ряд Фарея» . В Смите, Пол А .; Элленберг, Сэмюэл (ред.). Дзета-функция Римана . Чистая и прикладная математика. Нью-Йорк: Академическая пресса . стр. 263–267. ISBN 978-0-08-087373-2 . OCLC 316553016 . Проверено 30 сентября 2020 г.
^ Рутледж, Норман (март 2008 г.). «Вычислительная серия Фэри». Математический вестник . Том. 92, нет. 523. стр. 55–62.

Дальнейшее чтение

Хэтчер, Аллен (2022), Топология чисел , Провиденс, Род-Айленд: Американское математическое общество , ISBN 978-1470456115
Грэм, Рональд Л .; Кнут, Дональд Э .; Паташник, Орен (1989). Конкретная математика: основа информатики (2-е изд.). Бостон, Массачусетс: Аддисон-Уэсли. стр. 115–123, 133–139, 150, 462–463, 523–524. ISBN 0-201-55802-5 . — в частности, см. §4.5 (с. 115–123), Бонусная задача 4.61 (с. 150, 523–524), §4.9 (с. 133–139), §9.3, Задача 9.3.6 (с. 462– 463).
Вепстас, Линас. «Вопросительный знак Минковского, GL (2, Z) и модульная группа» (PDF) . - рассмотрены изоморфизмы Дерева Штерна-Броко.
Вепстас, Линас. «Симметрии карт удвоения периода» (PDF) . - рассматривает связи между фракциями Фари и фракталами.
Кобели, Кристиан; Захареску, Александру (2003). «Последовательность Хароса – Фэри через двести лет. Обзор». Акта Univ. Апуленсис Матем. Информ. (5): 1–38. «Стр. 1–20» (PDF) . Акта Univ. Апуленсис . «Стр. 21–38» (PDF) . Акта Univ. Апуленсис .
Матвеев, Андрей О. (2017). Последовательности Фарея: двойственность и карты между подпоследовательностями . Берлин, Германия: Де Грюйтер. ISBN 978-3-11-054662-0 . Исправления + код

Внешние ссылки

Хэтчер, Аллен. «Топология чисел» (PDF) . Онлайн-копия книги
Богомольный, Александр . «Серия Фэйри» . Разрезать узел .
Богомольный, Александр . «Дерево Штерна-Броко» . Разрезать узел .
Пеннестри, Этторе. «Таблица Броко с основанием 120» .
«Ряд Фэри» , Математическая энциклопедия , EMS Press , 2001 [1994]
Вайсштейн, Эрик В. «Дерево Штерна-Броко» . Математический мир .
Последовательность OEIS A005728 (количество дробей в ряду Фарея порядка n)
Последовательность OEIS A006842 (Числители ряда Фарея порядка n)
Последовательность OEIS A006843 (знаменатели ряда Фарея порядка n)
Архивировано в Ghostarchive и Wayback Machine : Бонаон, Фрэнсис . Веселые дроби и круги Форда (видео). Брэйди Харан . Проверено 9 июня 2015 г. - через YouTube.

[2] « Последовательность всех приведенных дробей со знаменателями, не превышающими n, перечисленных в порядке их размера, называется последовательностью Фарея порядка n. С комментарием: « Это определение последовательностей Фарея кажется наиболее удобным. Однако некоторые авторы предпочитают ограничивать дроби интервалом от 0 до 1 ». — Нивен и Цукерман (1972). ^{[ 1 ]}

[1] Нивен Иван М. ; Цукерман, Герберт С. (1972). Введение в теорию чисел (Третье изд.). Джон Уайли и сыновья. Определение 6.1.

[3] Гутери, Скотт Б. (2011). «1. Медиант» . Мотив математики: история и применение медианы и последовательности Фарея . Бостон: Доцент Пресс. п. 7. ISBN 978-1-4538-1057-6 . OCLC 1031694495 . Проверено 28 сентября 2020 г.

[4] Харди, штат Джорджия ; Райт, Э.М. (1979). Введение в теорию чисел (Пятое изд.). Издательство Оксфордского университета. Глава III . ISBN 0-19-853171-0 .

[Beiler-5] Перейти обратно: ^а ^б Бейлер, Альберт Х. (1964). Отдых в теории чисел (второе изд.). Дувр. Глава XVI. ISBN 0-486-21096-0 . Цитируется в «Сериал о Фэйри, история» . Разрезать узел .

[6] Слоан, Нью-Джерси (ред.). «Последовательность A005728» . Электронная энциклопедия целочисленных последовательностей . Фонд ОЭИС.

[Tomas2024-7] Томас Гарсия, Рохелио (июль 2024 г.). «Дроби Фэри с равными числителями и рангом единичных дробей» (PDF) . Целые числа . 24 .

[Tomas2018-8] Перейти обратно: ^а ^б Томас, Рохелио (январь 2022 г.). «Частичные суммы Франеля» (PDF) . Журнал целочисленных последовательностей . 25 (1).

[Austin2008-9] Остин, Дэвид (декабрь 2008 г.). «Деревья, зубы и время: математика изготовления часов» . Американское математическое общество . Род-Айленд. Архивировано из оригинала 4 февраля 2020 года . Проверено 28 сентября 2020 г.

[10] Мартин, Грег (2009). «Произведение значений гамма-функции на дроби с одинаковым знаменателем». arXiv : 0907.4384 [ math.CA ].

[11] Вемайер, Стефан (2009). «LCM(1,2,...,n) как произведение синусоидальных значений, выбранных по точкам в последовательностях Фарея». arXiv : 0909.1838 [ math.CA ].

[TomasGarcia2020-12] Томас Гарсия, Рохелио (август 2020 г.). «Равенства между наибольшими общими делителями, включающими три пары взаимно простых чисел» (PDF) . Заметки по теории чисел и дискретной математике . 26 (3): 5–7. дои : 10.7546/nntdm.2020.26.3.5-7 . S2CID 225280271 .

[13] «Приближение Фарея» . NRICH.maths.org . Архивировано из оригинала 19 ноября 2018 года . Проверено 18 ноября 2018 г.

[14] Элиаху, Шалом (август 1993 г.). «Проблема 3x+1: новые нижние оценки нетривиальных длин циклов» . Дискретная математика . 118 (1–3): 45–56. дои : 10.1016/0012-365X(93)90052-U .

[15] Чжэньхуа Ли, А.; Хартер, РГ (2015). «Квантовое возрождение осцилляторов Морса и геометрии Фарея – Форда». хим. Физ. Летт . 633 : 208–213. arXiv : 1308.4470 . Бибкод : 2015CPL...633..208L . дои : 10.1016/j.cplett.2015.05.035 . S2CID 66213897 .

[16] Томас, Р. (2014). «От последовательностей Фэрея к резонансным диаграммам» (PDF) . Специальные темы Physical Review — Ускорители и пучки . 17 (1): 014001. Бибкод : 2014PhRvS..17a4001T . doi : 10.1103/PhysRevSTAB.17.014001 .

[17] Харабор, Дэниел Дамир; Грастиен, Альбан; Собственный, Религиозный; Аксакалли, Вурал (26 мая 2016 г.). «Оптимальный поиск пути под любым углом на практике» . Журнал исследований искусственного интеллекта . 56 : 89–118. дои : 10.1613/jair.5007 .

[18] Хью, Патрик Чисан (19 августа 2017 г.). «Длина кратчайших путей вершин в двоичных сетках занятости по сравнению с кратчайшими r -ограниченными» . Журнал исследований искусственного интеллекта . 59 : 543–563. дои : 10.1613/jair.5442 .

[Tomas2020-19] Томас, Рохелио (2020). «Недочеты и исправления». arXiv : 2006.10661 [ physical.acc-ph ].

[20] Франель, Джером (1924). «Сюиты Фарея и проблема имен премьер» . Новости Общества наук в Геттингене . Математико-физический класс (на французском языке): 198–201.

[21] Ландау, Эдмунд (1924). «Замечания к вышеуказанному трактату г-на Франеля» . Новости Общества наук в Геттингене . Математико-физический класс (на немецком языке): 202–206.

[22] Блейк, Джин А. (1966). «Некоторые характерные свойства ряда Фарея». Американский математический ежемесячник . 73 (1): 50–52. дои : 10.2307/2313922 . JSTOR 2313922 .

[23] Курт Герстмайр; Гистмайр, Курт (2010). «Суммы Фарея и суммы Дедекинда». Американский математический ежемесячник . 117 (1): 72–78. дои : 10.4169/000298910X475005 . JSTOR 10.4169/000298910X475005 . S2CID 31933470 .

[24] Холл, РР; Шиу, П. (2003). «Индекс последовательности Фарея» . Мичиганская математика. Дж . 51 (1): 209–223. дои : 10.1307/mmj/1049832901 .

[25] Эдвардс, Гарольд М. (1974). «12.2 Сборник. Гипотеза Римана и ряд Фарея» . В Смите, Пол А .; Элленберг, Сэмюэл (ред.). Дзета-функция Римана . Чистая и прикладная математика. Нью-Йорк: Академическая пресса . стр. 263–267. ISBN 978-0-08-087373-2 . OCLC 316553016 . Проверено 30 сентября 2020 г.

[26] Рутледж, Норман (март 2008 г.). «Вычислительная серия Фэри». Математический вестник . Том. 92, нет. 523. стр. 55–62.

[ а ]

[ 2 ]

[ 3 ]

[ 4 ]

[ 5 ]

[ 6 ]

[ 7 ]

[ 8 ]

[ 9 ]

[ 10 ]

[ 11 ]

[ 12 ]

[ 13 ]

[ 14 ]

[ 15 ]

[ 16 ]

[ 17 ]

[ 18 ]

[ 19 ]

[ 20 ]

[ 21 ]

[ 22 ]

[ 23 ]

[ 24 ]

[ 25 ]

[ 1 ]