Синусоидальная плоская волна

В физике синусоидальная плоская волна — это частный случай плоской волны : поле , значение которого меняется как синусоидальная функция времени и расстояния от некоторой фиксированной плоскости. Ее также называют монохроматической плоской волной с постоянной частотой (как в монохроматическом излучении ).

Базовое представление

На любую должность ${\vec {x}}$ в пространстве и в любое время $t$ , значение такого поля можно записать как $F({\vec {x}},t)=A\cos \left(2\pi \nu ({\vec {x}}\cdot {\hat {n}}-ct)+\varphi \right)$ где ${\hat {n}}$ — вектор единичной длины , направление распространения волны, а « $\cdot$ " обозначает скалярное произведение двух векторов. Параметр $A$ , которая может быть скаляром или вектором, называется амплитудой волны; коэффициент $\nu$ , положительная скалярная величина, ее пространственная частота ; и аразмерный скаляр $\varphi$ , угол в радианах, является его начальной фазой или фазовым сдвигом .

Скалярная величина $d={\vec {x}}\cdot {\hat {n}}$ дает (со знаком) смещение точки ${\vec {x}}$ из плоскости, перпендикулярной ${\hat {n}}$ и проходит через начало системы координат. Эта величина постоянна в каждой плоскости, перпендикулярной ${\hat {n}}$ .

Во время $t=0$ , поле $F$ меняется в зависимости от смещения $d$ как синусоидальная функция $F({\vec {x}},0)=A\cos \left(2\pi \nu ({\vec {x}}\cdot {\hat {n}})+\varphi \right)$ Пространственная частота $\nu$ - количество полных циклов на единицу длины по направлению ${\hat {n}}$ . Для любого другого значения $t$ значения полей смещаются на расстояние $ct$ в направлении ${\hat {n}}$ . То есть кажется, что все поле движется в этом направлении со скоростью $c$ .

За каждое перемещение $d$ , движущаяся плоскость, перпендикулярная ${\hat {n}}$ на расстоянии $d+ct$ от начала координат, называется волновым фронтом . Этот самолет лежит на расстоянии $d$ от начала, когда $t=0$ , и движется в направлении ${\hat {n}}$ еще и со скоростью $c$ ; и тогда значение поля будет одинаковым и постоянным во времени в каждой его точке.

Синусоидальная плоская волна может быть подходящей моделью звуковой волны в объеме воздуха, малом по сравнению с расстоянием до источника (при условии, что нет эха от близких объектов). В этом случае $F({\vec {x}},t)\,$ было бы скалярным полем, отклонение давления воздуха в точке ${\vec {x}}$ и время $t$ , от нормального уровня.

В любой фиксированной точке ${\vec {x}}$ , поле также будет изменяться со временем синусоидально; это будет скалярное кратное амплитуды $A$ , между $+A$ и $-A$

Когда амплитуда $A$ – вектор, ортогональный ${\hat {n}}$ , волна называется поперечной . Такие волны могут проявлять поляризацию , если $A$ может быть ориентирован по двум неколлинеарным направлениям . Когда $A$ является вектором, коллинеарным ${\hat {n}}$ , волна называется продольной . Эти две возможности иллюстрируются S-волнами (поперечными) и P-волнами (давления), изучаемыми в сейсмологии .

Приведенная выше формула дает чисто «кинематическое» описание волны без ссылки на какой-либо физический процесс, который может вызывать ее движение. В механической или электромагнитной волне, распространяющейся в изотропной среде, вектор ${\hat {n}}$ Очевидное распространение волны — это также направление, в котором на самом деле течет энергия или импульс. Однако в анизотропной среде эти два направления могут быть разными . (См. Также: Волновой вектор # Направление волнового вектора .)

Альтернативные представления

Та же плоская синусоидальная волна $F$ вышеприведенное также можно выразить через синус вместо косинуса, используя элементарное тождество $\cos a=\sin(a+\pi /2)$ $F({\vec {x}},t)=A\sin \left(2\pi \nu ({\vec {x}}\cdot {\hat {n}}-ct)+\varphi '\right)$ где $\varphi '=\varphi +\pi /2$ . Таким образом, величина и смысл фазового сдвига зависят от того,волна определяется в терминах синуса или косинуса.

Добавление любого целого числа, кратного $2\pi$ к начальному этапу $\varphi$ не оказывает никакого влияния на поле. Добавление нечетного кратного $\pi$ имеет тот же эффект, что и отрицание амплитуды $A$ . Присвоение отрицательного значения пространственной частоте $\nu$ имеет эффект изменения направления распространения при соответствующей настройке начальной фазы.

По мере увеличения t волна движется вправо, и значение в данной точке x колеблется синусоидально .

Анимация 3D плоской волны. Каждый цвет представляет собой отдельную фазу волны.

Формулу синусоидальной плоской волны можно записать и несколькими другими способами:

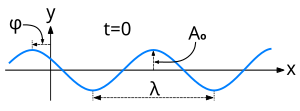
$F({\vec {x}},t)=A\cos(2\pi [({\vec {x}}\cdot {\hat {n}})/\lambda -t/T]+\varphi )$ Здесь $\lambda =1/\nu$ длина волны , расстояние между двумя волновыми фронтами, где поле равно амплитуде $A$ ; и $T=\lambda /c$ - это период изменения поля во времени, наблюдаемый в любой фиксированной точке пространства. Это взаимно $f=1/T$ - временная частота волны, измеряемая в полных циклах в единицу времени.
$F({\vec {x}},t)=A\cos(k({\vec {x}}\cdot {\hat {n}})-\omega t+\varphi )$ Здесь $k=2\pi \nu =2\pi /\lambda$ - это параметр, называемый угловым волновым числом (измеряется в радианах на единицу длины), и $\omega =2\pi /T$ — угловая частота изменения в фиксированной точке (в радианах в единицу времени).
$F({\vec {x}},t)=A\cos(2\pi ({\vec {x}}\cdot {\vec {\nu }})-\omega t+\varphi )$ где ${\vec {\nu }}=\nu {\hat {n}}={\hat {n}}/\lambda$ — вектор пространственной частоты или волновой вектор , трёхмерный вектор ${\vec {\nu }}=(\nu _{1},\nu _{2},\nu _{3})$ где $\nu _{i}$ - это количество полных циклов, которые происходят на единицу длины в любой фиксированный момент времени вдоль любой прямой, параллельной оси координат. $i$ .

Сложная экспоненциальная форма

Плоскую синусоидальную волну также можно выразить через комплексную показательную функцию $e^{\mathrm {i} z}=\exp(\mathrm {i} z)=\cos z+\mathrm {i} \sin z$ где $e$ является основанием натуральной показательной функции , а $\mathrm {i}$ — мнимая единица , определяемая уравнением $\mathrm {i} ^{2}=-1$ . С помощью этих инструментов можно определить сложную экспоненциальную плоскую волну как $U({\vec {x}},t)\;=\;A\exp[\mathrm {i} (2\pi \nu ({\vec {x}}\cdot {\hat {n}}-ct)+\varphi )]\;=\;A\exp[\mathrm {i} (2\pi {\vec {x}}\cdot {\vec {v}}-\omega t+\varphi )]$ где $A,\nu ,{\hat {n}},c,{\vec {v}},\omega ,\varphi$ такие же, как для (реальной) синусоидальной плоской волны.Это уравнение дает поле $U({\vec {x}},t)$ значением которого является комплексное число или вектор с комплексными координатами. Исходное волновое выражение теперь является просто реальной частью. $F({\vec {x}},t)=\operatorname {Re} {\left[U({\vec {x}},t)\right]}$

Чтобы оценить связь этого уравнения с предыдущими, ниже приведено то же самое уравнение, выраженное с использованием синусов и косинусов. Обратите внимание, что первый член соответствует реальной форме только что обсуждавшейся плоской волны.

${\begin{array}{rcccc}U({\vec {x}},t)&=&A\cos(2\pi \nu {\hat {n}}\cdot {\vec {x}}-\omega t+\varphi )&+&\mathrm {i} A\sin(2\pi \nu {\hat {n}}\cdot {\vec {x}}-\omega t+\varphi )\\[1ex]U({\vec {x}},t)&=&F({\vec {x}},t)&+&\mathrm {i} A\sin(2\pi \nu {\hat {n}}\cdot {\vec {x}}-\omega t+\varphi )\end{array}}$

Введенную комплексную форму плоской волны можно упростить, используя комплексную амплитуду $C\,$ подставьте действительную амплитуду $A\,$ .
В частности, поскольку комплексная форма $\exp[\mathrm {i} (2\pi {\vec {x}}\cdot {\vec {v}}-\omega t+\varphi )]\;=\;\exp[\mathrm {i} (2\pi \nu {\hat {n}}\cdot {\vec {x}}-\omega t)]\,e^{\mathrm {i} \varphi }$ можно поглотить фазовый фактор $e^{\mathrm {i} \varphi }$ в комплексную амплитуду, позволяя $C=Ae^{\mathrm {i} \varphi }$ , что приводит к более компактному уравнению $U({\vec {x}},t)=C\exp[\mathrm {i} (2\pi {\vec {x}}\cdot {\vec {v}}-\omega t)]$

Хотя комплексная форма имеет мнимую составляющую, после выполнения необходимых вычислений в комплексной плоскости ее реальное значение (которое соответствует волне, которую можно фактически физически наблюдать или измерять) может быть извлечено, что дает уравнение с действительным знаком, представляющее реальную плоскую волну. . $\operatorname {Re} [U({\vec {x}},t)]=F({\vec {x}},t)=A\cos(2\pi \nu {\hat {n}}\cdot {\vec {x}}-\omega t+\varphi )$

Основная причина, по которой предпочитают работать со сложной экспоненциальной формой плоских волн, заключается в том, что со сложными экспонентами часто алгебраически легче работать, чем с тригонометрическими синусами и косинусами. В частности, правила сложения углов для экспонент чрезвычайно просты.

Кроме того, при использовании методов анализа Фурье для волн в среде с потерями результирующее затухание легче обрабатывать с помощью комплексных коэффициентов Фурье . Если волна распространяется через среду с потерями, амплитуда волны больше не является постоянной, и, следовательно, волна, строго говоря, больше не является настоящей плоской волной.

В квантовой механике решения волнового уравнения Шредингера по своей природе являются комплексными и в простейшем случае принимают форму, идентичную приведенному выше представлению комплексных плоских волн. Однако мнимая составляющая в данном случае введена не в целях математической целесообразности, а фактически является неотъемлемой частью «волны».

В специальной теории относительности можно использовать еще более компактное выражение, используя четыре вектора .

Четырехпозиционный ${\vec {x}}=(ct,{\vec {x}})$
Четырехволновой вектор $2\pi \nu {\hat {n}}=\left({\frac {\omega }{c}},2\pi \nu {\hat {n}}\right)$
Скалярное произведение $2\pi \nu {\hat {n}}\cdot {\vec {x}}=\omega t-2\pi \nu {\hat {n}}\cdot {\vec {x}}$

Таким образом, $U({\vec {x}},t)=C\exp[\mathrm {i} (2\pi \nu {\hat {n}}\cdot {\vec {x}}-\omega t)]$ становится $U({\vec {x}})=C\exp[-\mathrm {i} (2\pi \nu {\hat {n}}\cdot {\vec {x}})]$

Приложения

Уравнения, описывающие электромагнитное излучение в однородной диэлектрической среде, допускают в качестве специальных решений плоские синусоидальные волны. В электромагнетизме поле $F$ обычно это электрическое поле , магнитное поле или векторный потенциал , который в изотропной среде перпендикулярен направлению распространения. ${\hat {n}}$ . Амплитуда $A$ тогда это вектор той же природы, равный полю максимальной силы. Скорость распространения $c$ будет скорость света в среде.

Уравнения, описывающие колебания однородного упругого твердого тела, допускают также решения в виде синусоидальных плоских волн, как поперечных, так и продольных. Эти два типа имеют разные скорости распространения, которые зависят от плотности и параметров Ламе среды.

Тот факт, что среда налагает скорость распространения, означает, что параметры $\omega$ и $k$ должно удовлетворять дисперсионному соотношению, характерному для среды. Дисперсионное соотношение часто выражается как функция: $\omega (k)$ . Соотношение $\omega /|k|$ дает величину фазовой скорости и производную $\partial \omega /\partial k$ дает групповую скорость . Для электромагнетизма в изотропной среде с показателем преломления $r$ , фазовая скорость равна $c/r$ , что равно групповой скорости, если индекс не зависит от частоты.

В линейных однородных средах общее решение волнового уравнения может быть выражено как суперпозиция синусоидальных плоских волн. Этот подход известен как метод углового спектра . Форма плосковолнового решения на самом деле является общим следствием трансляционной симметрии . В более общем смысле, для периодических структур, имеющих дискретную трансляционную симметрию, решения принимают форму волн Блоха , наиболее известных в кристаллических атомных материалах, но также в фотонных кристаллах и других периодических волновых уравнениях. Еще одно обобщение: для структур, однородных только в одном направлении. $x$ (например, волновод вдоль $x$ направлении) решения (волноводные моды) имеют вид $exp[i(kx-\omega t)]$ умноженный на некоторую амплитудную функцию $a(y,z)$ . Это частный случай сепарабельного уравнения в частных производных .

Поляризованные электромагнитные плоские волны

Линейно поляризованный свет

Кругополяризованный свет

Блоки векторов показывают, насколько величина и направление электрического поля постоянны для всей плоскости, перпендикулярной направлению движения.

На первой иллюстрации справа изображена линейно поляризованная электромагнитная волна . Поскольку это плоская волна, каждый синий вектор , указывающий перпендикулярное смещение от точки на оси к синусоидальной волне, представляет величину и направление электрического поля для всей плоскости, перпендикулярной оси.

На второй иллюстрации представлена с круговой поляризацией плоская электромагнитная волна . Каждый синий вектор, указывающий перпендикулярное смещение от точки оси к спирали, также представляет величину и направление электрического поля для всей плоскости, перпендикулярной оси.

На обеих иллюстрациях вдоль осей расположен ряд более коротких синих векторов, которые представляют собой уменьшенные версии более длинных синих векторов. Эти более короткие синие векторы экстраполируются в блок черных векторов, заполняющих объем пространства. Обратите внимание, что для данной плоскости черные векторы идентичны, что указывает на то, что величина и направление электрического поля постоянны вдоль этой плоскости.

В случае линейно поляризованного света напряженность поля от плоскости к плоскости меняется от максимума в одном направлении до нуля, а затем снова возрастает до максимума в противоположном направлении.

В случае света с круговой поляризацией напряженность поля остается постоянной от плоскости к плоскости, но ее направление постоянно меняется по принципу вращения.

Ни на одной из иллюстраций не указано соответствующее электрическому полю магнитное поле , которое пропорционально напряженности электрическому полю в каждой точке пространства, но расположено к нему под прямым углом. Иллюстрации векторов магнитного поля были бы практически идентичны этим, за исключением того, что все векторы были бы повернуты на 90 градусов вокруг оси распространения так, чтобы они были перпендикулярны как направлению распространения, так и вектору электрического поля.

Отношение амплитуд компонент электрического и магнитного поля плоской волны в свободном пространстве известно как волновое сопротивление свободного пространства , равное 376,730313 Ом.

См. также

Ссылки

Дж. Д. Джексон, Классическая электродинамика (Wiley: Нью-Йорк, 1998).
Л. М. Бреховских, "Волны в слоистых средах", Серия: Прикладная математика и механика, Т. 16, (Академик Пресс, 1980).