Химическое уравнение
Эта статья включает список общих ссылок , но в ней отсутствуют достаточные соответствующие встроенные цитаты . ( Октябрь 2023 г. ) |
Химическое уравнение — это символическое представление химической реакции в виде символов и химических формул . Реагенты . указаны слева, а продукты — справа, со знаком плюса между объектами как в реагентах, так и в продуктах, а также стрелкой, указывающей на продукты, чтобы указать направление движения реакция. [1] Химические формулы могут быть символическими, структурными (иллюстрированные диаграммы) или смешанными. Коэффициенты рядом с символами и формулами сущностей представляют собой абсолютные значения стехиометрических чисел . Первое химическое уравнение было составлено Жаном Бегеном в 1615 году. [2]
Структура [ править ]
Химическое уравнение (см. пример ниже) состоит из списка реагентов (исходных веществ) в левой части, символа стрелки и списка продуктов (веществ, образующихся в химической реакции) в правой части. . Каждое вещество определяется своей химической формулой , которой может предшествовать число, называемое стехиометрическим коэффициентом . [а] Коэффициент указывает, сколько объектов (например, молекул ) этого вещества участвует в реакции на молекулярной основе. Если не написано явно, коэффициент равен 1. Несколько веществ в любой части уравнения отделяются друг от друга знаком плюс .
уравнение реакции соляной кислоты с натрием В качестве примера можно обозначить :
- 2HCl + 2Na → 2NaCl + H2
Учитывая, что формулы довольно просты, это уравнение можно прочитать как «два HCL плюс два NA дают доходность». [б] два NACL и H два». Альтернативно, как правило, для уравнений, включающих сложные химические вещества, химические формулы читаются с использованием номенклатуры IUPAC , которая может выразить это уравнение в словах как «две молекулы соляной кислоты и два атома натрия реагируют с образованием двух формульных единиц натрия ». хлорид и молекула газообразного водорода ».
Типы реакций [ править ]
Для обозначения типа реакции используются разные варианты символа стрелки: [1]
чистая форвардная реакция реакция в обе стороны [с] равновесие [д] стехиометрическое соотношение резонанс (не реакция)
Состояние материи [ править ]
Чтобы указать физическое состояние химического вещества, к его формуле можно добавить символ в скобках: (s) для твердого тела, (l) для жидкости, (g) для газа и (водный раствор) для водного раствора . Это особенно делается, когда кто-то хочет подчеркнуть состояния или их изменения. Например, реакция водного раствора соляной кислоты с твердым (металлическим) натрием с образованием водного раствора хлорида натрия и газообразного водорода будет записываться так:
- 2HCl(водн.) + 2Na(тв) → 2NaCl(водн.) + H 2 (г)
Эта реакция имела бы другие термодинамические и кинетические свойства, если бы газообразный хлористый водород заменил соляную кислоту в качестве реагента:
- 2HCl(г) + 2Na(т) → 2NaCl(т) + H 2 (г)
Альтернативно, стрелка без скобок в некоторых случаях используется для обозначения образования газа ↑ или осадка ↓. Это особенно полезно, если образуется только один такой вид. Вот пример, показывающий, что образуется газообразный водород:
- 2HCl + 2Na → 2 NaCl + H 2 ↑
Катализ и другие условия [ править ]
Если реакция требует энергии, это указано над стрелкой. Заглавная греческая буква дельта (Δ) или треугольник (△). [и] Нанесен на стрелку реакции, чтобы показать, что в реакцию добавляется энергия в виде тепла. Выражение hν [ф] используется как символ добавления энергии в форме света. Другие символы используются для других конкретных типов энергии или излучения.
Аналогично, если для реакции требуется определенная среда с определенными специфическими характеристиками, то над стрелкой можно поместить название кислоты или основания, которое используется в качестве среды. Если не требуется конкретная кислота или основание, другой способ обозначить использование кислой или основной среды — написать H. + или ОН − (или даже «кислота» или «основание») на вершине стрелки. Таким же образом могут быть указаны конкретные условия температуры и давления, а также наличие катализаторов.
Варианты обозначений [ править ]

Стандартные обозначения химических уравнений допускают только все реагенты с одной стороны, все продукты с другой и все стехиометрические коэффициенты положительные. уравнения дегидратации метанола Например, обычная форма в диметиловый эфир :
- 2 CH 3 OH → CH 3 OCH 3 + H 2 O
Иногда используется расширение, в котором некоторые вещества с их стехиометрическими коэффициентами перемещаются выше или ниже стрелки, которым предшествует знак плюс или ничего для реагента и знак минус для продукта. Тогда то же уравнение может выглядеть так:
Такие обозначения служат для того, чтобы скрыть менее важные вещества от сторон уравнения, сделать тип рассматриваемой реакции более очевидным и облегчить составление цепочек химических уравнений. многоступенчатых Это очень полезно для иллюстрации механизмов реакций . Обратите внимание, что вещества, расположенные выше или ниже стрелок, в данном случае не являются катализаторами , поскольку расходуются или производятся в реакции так же, как обычные реагенты или продукты.
Другое расширение, используемое в механизмах реакций, перемещает некоторые вещества к ветвям стрелки. Оба расширения используются в примере иллюстрации механизма.
Использование отрицательных стехиометрических коэффициентов по обе стороны уравнения (как в примере ниже) не получило широкого распространения и часто не рекомендуется. [5] [ нужен лучший источник ]
химических Балансировка уравнений
Поскольку ядерных реакций в химической реакции не происходит , химические элементы проходят реакцию в неизмененном виде. Таким образом, каждая часть химического уравнения должна представлять одинаковое количество атомов любого конкретного элемента (или нуклида разные изотопы , если учитывать ). То же самое справедливо и для полного электрического заряда , как утверждает закон сохранения заряда . Уравнение, удовлетворяющее этим требованиям, называется сбалансированным .
Химическое уравнение балансируется путем присвоения подходящих значений стехиометрическим коэффициентам. Простые уравнения можно сбалансировать путем проверки, то есть методом проб и ошибок. Другой метод предполагает решение системы линейных уравнений .
Сбалансированные уравнения обычно записываются с наименьшими натуральными коэффициентами. Однако иногда может оказаться выгодным принять дробный коэффициент, если он упростит другие коэффициенты. Таким образом, вводный пример можно переписать как
В некоторых случаях дробные коэффициенты даже неизбежны. Например, реакцию, соответствующую стандартной энтальпии образования, нужно записать так, чтобы образовалась одна молекула одного продукта. Это часто требует, чтобы некоторые коэффициенты реагентов были дробными, как в случае с образованием фторида лития :
Метод проверки [ править ]
4 + 2 О
2 → CO
2 + 2 ч
2 O , со стороны продуктов необходимо поставить коэффициент 2 перед газообразным кислородом со стороны реагентов и перед водой , чтобы по закону сохранения массы количество каждого элемента не менялось в ходе реакции.
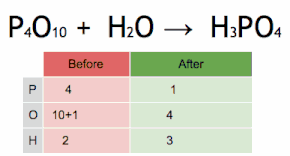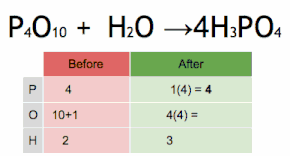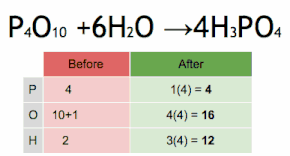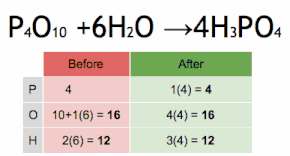
Это химическое уравнение балансируется путем умножения H 3 PO 4 на четыре, чтобы соответствовать количеству атомов P, а затем умножения H 2 O на шесть, чтобы соответствовать количеству атомов H и O.
Метод проверки можно описать как установку стехиометрического коэффициента самого сложного вещества равным 1 и пошаговое присвоение значений другим коэффициентам так, чтобы обе части уравнения в конечном итоге содержали одинаковое количество атомов для каждого элемента. Если в ходе этого процесса возникают какие-либо дробные коэффициенты, то наличие дробей можно исключить (в любой момент) умножением всех коэффициентов на их наименьший общий знаменатель .
- Пример
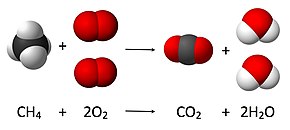
химического уравнения полного сгорания метана Балансировка
достигается следующим образом:
- Перед самой сложной формулой ( СН 4 ) ставится коэффициент 1:
- В левой части находится 1 атом углерода , поэтому 1 молекула CO 2 уравновесит его. В левой части также находятся 4 атома водорода , которые будут уравновешены 2 молекулами H 2 O :
- Уравновешивание 4 атомов кислорода в правой части 2 молекулами O 2 дает уравнение
- Коэффициенты, равные 1, опущены, так как их не нужно указывать явно:
- Целесообразно проверить, что окончательное уравнение сбалансировано, т.е. что для каждого элемента имеется одинаковое количество атомов слева и справа: 1 атом углерода, 4 водорода и 4 кислорода.
Система линейных уравнений [ править ]
Для каждого химического элемента (или нуклида, или неизмененной части или заряда) i требование его сохранения может быть выражено математическим уравнением
где
- a ij — количество атомов элемента i в молекуле вещества j (по формуле химического уравнения), а
- s j – стехиометрический коэффициент вещества j .
В результате получается однородная система линейных уравнений , которые легко решаются математическими методами. , состоящее из всех нулей Такая система всегда имеет тривиальное решение , которое нас не интересует, но если и существуют дополнительные решения, то их будет бесконечное количество. Любое нетривиальное решение уравновесит химическое уравнение. «Предпочтительным» решением является решение с целым числом , в основном положительным. [г] стехиометрические коэффициенты s j с наибольшим общим делителем, равным единице.
Пример [ править ]
Присвоим переменные стехиометрическим коэффициентам химического уравнения из предыдущего раздела и запишем соответствующие линейные уравнения:
Все решения этой системы линейных уравнений имеют следующий вид, где r – любое действительное число :
Выбор r = 1 дает предпочтительное решение:
что соответствует сбалансированному химическому уравнению:
Матричный метод [ править ]
Система линейных уравнений, представленная в предыдущем разделе, также может быть записана с использованием эффективного матричного формализма. Сначала для унификации стехиометрических коэффициентов реагента и продукта s j введем величину
называется стехиометрическим числом , [час] что упрощает линейные уравнения до
где J – общее количество реагирующих и продуктовых веществ (формул) в химическом уравнении.
Размещение значений a ij в строке i и столбце j матрицы композиции
- А =
и расположение стехиометрических чисел в стехиометрический вектор
- п =
позволяет выразить систему уравнений в виде одного матричного уравнения :
- Ан = 0
Как и ранее, любой ненулевой стехиометрический вектор ν , который решает матричное уравнение, уравновешивает химическое уравнение.
Множество решений матричного уравнения представляет собой линейное пространство называемое ядром матрицы A. , Чтобы это пространство содержало ненулевые векторы ν , т. е. имело положительную размерность J N , столбцы матрицы композиции A не должны быть линейно независимыми . Тогда проблема балансировки химического уравнения становится проблемой определения J N -мерного ядра матрицы состава. Важно отметить, что только для J N = 1 будет существовать единственное предпочтительное решение задачи балансировки. При J N > 1 будет бесконечное число предпочтительных решений, причем J N из них линейно независимы. Если J N = 0, останется только непригодное тривиальное решение — нулевой вектор.
Были разработаны методы [6] [7] быстро вычислить набор J N независимых решений задачи балансировки, превосходящих инспекционный и алгебраический метод [ нужна ссылка ] в том смысле, что они являются определяющими и дают все решения проблемы балансировки.
- Пример
Снова используя то же химическое уравнение, запишите соответствующее матричное уравнение:
Его решения имеют следующий вид, где r — любое действительное число:
Выбор r = 1 и смена знака первых двух строк дает предпочтительное решение проблемы балансировки:
Ионные уравнения [ править ]
Ионное уравнение — это химическое уравнение, в котором электролиты записаны в виде диссоциированных ионов . Ионные уравнения используются для реакций одинарного и двойного замещения , протекающих в водных растворах .
Например, в следующей реакции осаждения:
полное ионное уравнение:
или, включая все физические состояния:
В этой реакции Ca 2+ и № 3 − ионы остаются в растворе и не участвуют в реакции. То есть эти ионы идентичны как со стороны реагента, так и со стороны продукта химического уравнения. Поскольку такие ионы не участвуют в реакции, их называют ионами-зрителями . Чистое ионное уравнение — это полное ионное уравнение, из которого удалены ионы-спектаторы. [8] Итоговое ионное уравнение протекающих реакций:
или, в уменьшенной сбалансированной форме,
В реакции нейтрализации или кислотно - основной реакции чистое ионное уравнение обычно будет иметь вид:
Есть несколько кислотно-основных реакций, в которых помимо молекулы воды, показанной выше, образуется осадок. Примером может служить реакция гидроксида бария с фосфорной кислотой , в результате которой образуется не только вода, но и нерастворимая соль фосфат бария . В этой реакции нет ионов-спектаторов, поэтому чистое ионное уравнение такое же, как и полное ионное уравнение.
Реакции двойного замещения, в которых карбонат реагирует с кислотой, имеют чистое ионное уравнение:
Если каждый ион является «ионом-наблюдателем», то реакции не было, и итоговое ионное уравнение равно нулю.
Обычно, если z j кратно элементарному заряду j-й молекулы, нейтральность заряда можно записать как:
где ν j — стехиометрические коэффициенты, описанные выше. Z включен j может быть [6] [7] в качестве дополнительной строки в матрице a ij, описанной выше, и тогда правильно сбалансированное ионное уравнение также будет подчиняться:
История [ править ]
Этот раздел пуст. Вы можете помочь, добавив к нему . ( июнь 2022 г. ) |
Набор текста [ править ]
Этот раздел пуст. Вы можете помочь, добавив к нему . ( июнь 2022 г. ) |
Примечания [ править ]
- ^ Не путать с родственной величиной, называемой стехиометрическим числом .
- ^ Не путать с выходом (химией) , количественной оценкой эффективности синтеза.
- ^ Обозначение ⇄ было предложено в 1884 году голландским химиком Якобусом Хенрикусом ван 'т Хоффом . Ван 'т-Гофф назвал реакции, не дошедшие до завершения, «ограниченными реакциями». Он написал (перевод с французского): [3]
Теперь г-н Пфаундлер объединил эти два явления в единую концепцию, рассматривая наблюдаемый предел как результат двух противоположных реакций, приводящих ту, что в приведенном примере, к образованию морской соли [т.е. NaCl] и азотной кислоты, [и ] другой к соляной кислоте и нитрату натрия. Это соображение, подтвержденное экспериментом, оправдывает выражение «химическое равновесие», которое используется для характеристики конечного состояния ограниченных реакций. Я бы предложил перевести это выражение следующим символом:
- HCl + NO 3 Na ⇄ NO 3 H + Cl Na.
Поэтому в данном случае я заменяю знак = в химическом уравнении знаком ⇄, который на самом деле не просто выражает равенство, но показывает также направление реакции. Это ясно выражает то, что химическое действие происходит одновременно в двух противоположных направлениях.
- ^ Обозначения был предложен Хью Маршаллом в 1902 году. [4]
- ^ Треугольник (△) изначально был алхимическим символом огня.
- ^ Это выражение происходит из энергии фотона уравнения Планка для E = hν . Греческую букву ν («ню») иногда ошибочно заменяют латинской буквой v («ве») .
- ^ Отрицательный стехиометрический коэффициент означает, что вещество находится в неправильной части химического уравнения.
- ^ Эквивалентный подход - поменять знаки a ij для реагентов вместо замены стехиометрических коэффициентов s j на стехиометрические числа ν j .
Ссылки [ править ]
- ^ Jump up to: Перейти обратно: а б ИЮПАК , Сборник химической терминологии , 2-е изд. («Золотая книга») (1997). Исправленная онлайн-версия: (2006–) « Уравнение химической реакции ». два : 10.1351/goldbook.C01034
- ^ Кросланд, член парламента (1959). «Использование диаграмм в качестве химических« уравнений »в лекциях Уильяма Каллена и Джозефа Блэка». Анналы науки . 15 (2): 75–90. дои : 10.1080/00033795900200088 .
- ^ Ван 'т Хофф, Дж. Х. (1884). Études de Dynamique Chemique [ Исследования химической динамики ] (на французском языке). Амстердам, Нидерланды: Frederik Muller & Co., стр. 4–5.
Теперь г-н Пфаундлер связал эти два явления... совершающиеся одновременно в двух противоположных направлениях.
- ^ Маршалл, Хью (1902). «Предлагаемые модификации знака равенства для использования в химической записи». Труды Королевского общества Эдинбурга . 24 : 85–87. дои : 10.1017/S0370164600007720 .
- ^ «Почему в уравнениях реакций нельзя использовать знак минус (-)?» . Обмен стеками . 20 сентября 2017 г. Ответ Николау Сакер Нето. Архивировано из оригинала 15 июня 2021 г.
- ^ Jump up to: Перейти обратно: а б Торн, Лоуренс Р. (2010). «Инновационный подход к балансировке уравнений химических реакций: упрощенный метод обращения матрицы для определения нулевого пространства матрицы». хим. Воспитатель . 15 : 304–308. arXiv : 1110.4321 .
- ^ Jump up to: Перейти обратно: а б Холмс, Дилан (2015). «Взгляд нулевого пространства на химический баланс» . Дилан Холмс . Проверено 10 октября 2017 г.
- ^ Джеймс Э. Брэди; Фредерик Сенезе; Нил Д. Джесперсен (14 декабря 2007 г.). Химия: вещество и его изменения . Джон Уайли и сыновья. ISBN 9780470120941 . LCCN 2007033355 .





![{\displaystyle {\ce {2CH3OH->[{\overset {}{\ce {-H2O}}}]CH3OCH3}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a9322a7fd3bb1fb28dab61d3c7fa287ab389d3c7)






























