Гомогенное отношение

В математике однородное отношение (также называемое эндоотношением ) на множестве X — это бинарное отношение между X оно является подмножеством декартова произведения $X \times X.$ и самим собой, т. е . ^[1]^[2]^[3] Обычно это формулируется как «отношение на X ». ^[4] или «(бинарное) отношение над X ». ^[5]^[6] Примером гомогенных отношений являются отношения родства , где отношения существуют между людьми.

Общие типы эндоотношений включают порядки , графы и эквивалентности . Специализированные исследования теории порядка и теории графов позволили развить понимание эндоотношений. Для описания используется терминология, специфичная для теории графов: предполагается, что обычный (неориентированный) граф соответствует симметричному отношению , а общее эндоотношение соответствует ориентированному графу . Эндореляция R соответствует логической матрице выражение xRy соответствует ребру между x и y в графе и 1 в квадратной матрице R из 0 и 1, где . она называется матрицей смежности В терминологии графов .

Особые однородные отношения

Некоторые частные однородные отношения над множеством X с произвольными элементами $, x1$ x2 $) ($ :

Пустое отношение
$Е = \emptyset$ ;
то есть $x 1 Ex 2$ никогда не выполняется;
Универсальное отношение
$U знак равно Икс \times Икс$ ;
то есть $x 1 Ux 2$ выполняется всегда;
Отношение тождества (см. также функцию тождества )
$я знак равно {(Икс, Икс) | х} € Икс$ ;
то есть $x 1 Ix 2$ выполняется тогда и только тогда, когда $x 1 = x 2$ .

Пример

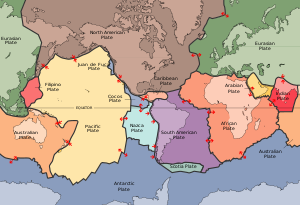
Пятнадцать крупных тектонических плит земной коры соприкасаются друг с другом в однородном отношении. Отношение может быть выражено в виде логической матрицы , где 1 указывает на контакт, а 0 - на отсутствие контакта. Этот пример выражает симметричное отношение.

Характеристики

Некоторые важные свойства, которыми может обладать однородное отношение $R$ над множеством $X$ :

Рефлексивный: для всех $x \in X$ , $xRx$ . Например, ≥ — рефлексивное отношение, а > — нет.
Иррефлексивный (или строгий ): для всех $x \in X$ , а не $xRx$ . Например, > — иррефлексивное отношение, а ≥ — нет.
Coreflexive: для всех $x, y \in X$ , если $xRy,$ то $x = y$ . ^[7] Например, отношение целых чисел, в котором каждое нечетное число связано само с собой, является корефлексивным отношением. Отношение равенства является единственным примером как рефлексивного, так и кор-рефлексивного отношения, и любое кор-рефлексивное отношение является подмножеством отношения тождества.
Левый квазирефлексивный: для всех $x, y \in X$ , если $xRy$ , то $xRx$ .
Правый квазирефлексивный: для всех $x, y \in X$ , если $xRy$ , то $yRy$ .
Квазирефлекторно: для всех $x, y \in X$ , если $xRy,$ то $xRx$ и $yRy$ . Отношение является квазирефлексивным тогда и только тогда, когда оно одновременно квазирефлексивно слева и справа.

Предыдущие шесть альтернатив далеко не исчерпывающие; например, бинарное отношение $xRy,$ определяемое формулой $y = x 2$ не является ни иррефлексивным, ни корефлексивным, ни рефлексивным, поскольку содержит пары $(0, 0)$ и $(2, 4)$ , но не $(2, 2)$ соответственно. Последние два факта также исключают (любую) квазирефлексивность.

Симметричный: для всех $x, y \in X$ , если $xRy$ , то $yRx$ . Например, «является кровным родственником» является симметричным отношением, поскольку $x$ является кровным родственником $y$ тогда и только тогда, когда $y$ является кровным родственником $x$ .
антисимметричный: для всех $x, y \in X$ , если $xRy$ и $yRx$ , то $x = y$ . Например, ≥ — антисимметричное отношение; то же самое и >, но бессмысленно (условие в определении всегда ложно). ^[8]
Асимметричный: для всех $x, y \in X$ , если $xRy$ , то не $yRx$ . Отношение асимметрично тогда и только тогда, когда оно одновременно антисимметрично и иррефлексивно. ^[9] Например, > является асимметричным отношением, а ≥ – нет.

Опять же, предыдущие три альтернативы далеко не исчерпывающие; Например, отношение $xRy,$ определенное соотношением $x > 2,$ не является ни симметричным, ни антисимметричным, не говоря уже о асимметричном.

Переходный: для всех $x, y, z \in X$ , если $xRy$ и $yRz$ , то $xRz$ . Транзитивное отношение иррефлексивно тогда и только тогда, когда оно асимметрично. ^[10] Например, «является предком» является транзитивным отношением, а «является родителем» — нет.
антитранзитивный: для всех $x, y, z \in X$ , если $xRy$ и $yRz$ , то никогда $xRz$ .
Котранзитивный: если дополнение к R транзитивно. То есть для всех $x, y, z \in X$ , если $xRz$ , то $xRy$ или $yRz$ . Это используется в псевдозаказах в конструктивной математике.
Квазитранзитивный: для всех $x, y, z \in X$ , если $xRy$ и $yRz$ , но не $yRx$ и $zRy$ , то $xRz$ , но не $zRx$ .
Транзитивность несравнимости: для всех $x, y, z \in X$ , если $x$ и $y$ несравнимы относительно $R$ если то же самое верно для $y$ и $z$ , то $x$ и $z$ также несравнимы относительно $R.$ и Это используется в слабых порядках .

Опять же, предыдущие 5 альтернатив не являются исчерпывающими. Например, отношение $xRy$ if ( $y = 0$ или $y = x +1$ ) не удовлетворяет ни одному из этих свойств. С другой стороны, пустое отношение тривиально удовлетворяет им всем.

Плотный: для всех $x, y \in X$ таких, что $xRy$ , существует такой $z \in X,$ что $xRz$ и $zRy$ . Это используется в плотных заказах .
Подключено: для всех $x, y \in X$ , если $x \neq y,$ то $xRy$ или $yRx$ . Это свойство иногда ^{[ нужна ссылка ]} называется «всего», что отличается от определений «левый/правый-тот», приведенных ниже.
Сильно связаны: для всех $x, y \in X$ , $xRy$ или $yRx$ . Это свойство тоже иногда ^{[ нужна ссылка ]} называется «всего», что отличается от определений «левый/правый-тот», приведенных ниже.
Трихотомический: для всех $x, y \in X$ выполняется ровно одно из $xRy$ , $yRx$ или $x = y$ . Например, > является трихотомическим отношением к действительным числам, а отношение «делит» к натуральным числам - нет. ^[11]
Правильно-евклидово (или просто евклидово ): для всех $x, y, z \in X$ , если $xRy$ и $xRz$ , то $yRz$ . Например, = является евклидовым отношением, потому что если $x = y$ и $x = z,$ то $y = z$ .
Левый евклидов: для всех $x, y, z \in X$ , если $yRx$ и $zRx,$ то $yRz$ .
Обоснованный: каждое непустое подмножество $S$ множества $X$ содержит минимальный элемент относительно $R$ . Обоснованность подразумевает условие нисходящей цепи (т. е. никакой бесконечной цепи ... $x n R ... Rx 3 Rx 2 Rx 1$ не может существовать). Если принять аксиому зависимого выбора , то оба условия эквивалентны. ^[12]^[13]

Более того, все свойства бинарных отношений вообще могут быть применимы и к однородным отношениям:

Набор-подобный: для всех $x \in X$ — класс всех $y$ таких, что $yRx$ является множеством. (Это имеет смысл только в том случае, если разрешены отношения над собственными классами.)
Уникальный слева: для всех $x, z \in X$ и всех $y \in Y$ , если $xRy$ и $zRy$ , то $x = z$ .
Одновалентный: для всех $x \in X$ и всех $y, z \in Y$ , если $xRy$ и $xRz$ , то $y = z$ . ^[14]
Итого (также называемое левым итогом): для всех $x \in X$ существует $y \in Y$ такой, что $xRy$ . Это свойство отличается от определения связного ( также называют полным ). которое некоторые авторы ^{[ нужна ссылка ]}
Сюръективный (также называемый правототальным): для всех $y \in Y$ существует $x \in X$ такой, что xRy .

Предпорядок — это отношение, которое является рефлексивным и транзитивным. Полный предварительный порядок , также называемый линейным предварительным порядком или слабым порядком , — это отношение, которое является рефлексивным, транзитивным и связным.

Частичный порядок , также называемый порядком , ^{[ нужна ссылка ]} Это отношение рефлексивное, антисимметричное и транзитивное. Строгий частичный порядок , также называемый строгим порядком . ^{[ нужна ссылка ]} Это отношение, которое является иррефлексивным, антисимметричным и транзитивным. Полный порядок , также называемый линейным порядком , простым порядком или цепочкой , — это отношение, которое является рефлексивным, антисимметричным, транзитивным и связным. ^[15] Строгий тотальный порядок , также называемый строгим линейным порядком , строгим простым порядком или строгой цепочкой , — это отношение, которое является иррефлексивным, антисимметричным, транзитивным и связным.

Отношение частичной эквивалентности — это отношение, которое является симметричным и транзитивным. Отношение эквивалентности — это отношение, которое является рефлексивным, симметричным и транзитивным. Это также отношение симметричное, транзитивное и тотальное, поскольку эти свойства предполагают рефлексивность.

Последствия и конфликты между свойствами однородных бинарных отношений
Implications (blue) and conflicts (red) between properties (yellow) of homogeneous binary relations. For example, every asymmetric relation is irreflexive ("ASym ⇒ Irrefl"), and no relation on a non-empty set can be both irreflexive and reflexive ("Irrefl # Refl"). Omitting the red edges results in a Hasse diagram.

Операции

Если R — однородное отношение над множеством X , то каждое из следующих отношений является однородным отношением над X :

Рефлексивное закрытие , R ⁼: Определяется как $R = знак равно {(Икс, Икс) | x \in X} \cup R$ или наименьшее рефлексивное отношение над X содержащее R. , Можно доказать, что это равно пересечению всех рефлексивных отношений, содержащих R .
Рефлекторное сокращение , R ^≠: Определяется как $R ≠ знак равно р \ {( Икс , Икс ) | x ∈ X$ } или наибольшее иррефлексивное отношение над X, в R. содержащееся
Транзитивное замыкание , R ⁺: Определяется как наименьшее транзитивное отношение над X содержащее R. , Можно видеть, что это равно пересечению всех транзитивных отношений, содержащих R .
Рефлексивное транзитивное замыкание , R *: Определяется как $R * = (R +) =$ , наименьший предварительный заказ, содержащий R .
Рефлексивное транзитивное симметричное замыкание , R ^≡: Определяется как наименьшее отношение эквивалентности над X содержащее R. ,

Все операции, определенные в разделе «Двоичные отношения § Операции», также применимы к однородным отношениям.

Однородные отношения по собственности
	Рефлексивность	Симметрия	Транзитивность	Связность	Символ	Пример
Ориентированный граф					→
Неориентированный граф		Симметричный
Зависимость	Рефлексивный	Симметричный
Турнир	Бездумный	Асимметричный				Иерархия
Предварительный заказ	Рефлексивный		Переходный		≤	Предпочтение
Общий предзаказ	Рефлексивный		Переходный	Подключено	≤
Частичный заказ	Рефлексивный	антисимметричный	Переходный		≤	Подмножество
Строгий частичный порядок	Бездумный	Асимметричный	Переходный		<	Строгое подмножество
Общий заказ	Рефлексивный	антисимметричный	Переходный	Подключено	≤	Алфавитный порядок
Строгий общий порядок	Бездумный	Асимметричный	Переходный	Подключено	<	Строгий алфавитный порядок
Отношение частичной эквивалентности		Симметричный	Переходный
Отношение эквивалентности	Рефлексивный	Симметричный	Переходный		~, ≡	Равенство

Перечисление

Множество всех однородных отношений ${\mathcal {B}}(X)$ над множеством X — это множество $2 X \times X$ , которая является булевой алгеброй , дополненной инволюцией отображения отношения в обратное отношение . Рассматривая композицию отношений как бинарную операцию над ${\mathcal {B}}(X)$ , он образует моноид с инволюцией , где единичным элементом является тождественное отношение. ^[16]

Число различных однородных отношений над набором из n -элементов равно $2 н 2$ (последовательность A002416 в OEIS ):

Количество n -элементных бинарных отношений разных типов
Elements	Любой	Переходный	Рефлексивный	Симметричный	Предварительный заказ	Частичный заказ	Общий предзаказ	Общий заказ	Отношение эквивалентности
0	1	1	1	1	1	1	1	1	1
1	2	2	1	2	1	1	1	1	1
2	16	13	4	8	4	3	3	2	2
3	512	171	64	64	29	19	13	6	5
4	65,536	3,994	4,096	1,024	355	219	75	24	15
н	2 ^{н ²}		2 ^{п ( п -1)}	2 ^{п ( п +1)/2}			∑ ^н _{к = 0} к ! С ( п , к )	н !	∑ ^н _{k =0} S ( n , k )
ОЭИС	А002416	А006905	А053763	А006125	А000798	А001035	А000670	А000142	А000110

Обратите внимание, что S ( n , k ) относится к числам Стирлинга второго рода .

Примечания:

Количество иррефлексивных отношений такое же, как и рефлексивных.
Число строгих частичных порядков (иррефлексивных транзитивных отношений) такое же, как и частичных порядков.
Количество строгих слабых заказов такое же, как и общее количество предзаказов.
Общие заказы — это частичные заказы, которые также являются общими предзаказами. Таким образом, количество предзаказов, которые не являются ни частичным заказом, ни полным предзаказом, равно количеству предварительных заказов минус количество частичных заказов минус количество общих предзаказов плюс количество общих заказов: 0, 0, 0, 3 и 85 соответственно.
Число отношений эквивалентности — это количество разбиений , которое является числом Белла .

Однородные отношения можно сгруппировать в пары (отношение, дополнение ), за исключением того, что при $n = 0$ отношение является собственным дополнением. Несимметричные можно сгруппировать в четверки (отношение, дополнение, обратное , обратное дополнение).

Примеры

Орденские отношения , в том числе строгие приказы :
- Больше, чем
- Больше или равно
- Меньше, чем
- Меньше или равно
- Делит (равномерно)
- Подмножество
Отношения эквивалентности :
- Равенство
- Параллельно с (для аффинных пространств )
- Равномерность или «находится в биекции с»
- изоморфный
- Эквиполентные отрезки
Отношение толерантности — рефлексивное и симметричное отношение:
- Отношение зависимости , конечное отношение допуска.
- Отношение независимости — дополнение к некоторому отношению зависимости.
Родственные отношения

Обобщения

Бинарное отношение, вообще говоря, не обязательно должно быть однородным, оно определяется как подмножество R ⊆ X × Y для произвольных множеств X и Y .
Финитарное отношение — это подмножество R ⊆ X ₁ × ... × X _n для некоторого натурального числа n и произвольных множеств X ₁ , ..., X _n , его также называют n -арным отношением.

Ссылки

^ Майкл Винтер (2007). Категории Гогена: Категорический подход к L-нечетким отношениям . Спрингер. стр. x – xi. ISBN 978-1-4020-6164-6 .
^ М. Е. Мюллер (2012). Открытие реляционных знаний . Издательство Кембриджского университета. п. 22. ISBN 978-0-521-19021-3 .
^ Питер Дж. Пал; Рудольф Дамрат (2001). Математические основы вычислительной техники: Справочник . Springer Science & Business Media. п. 496. ИСБН 978-3-540-67995-0 .
^ Мордесон, Джон Н.; Наир, Премчанд С. (8 ноября 2012 г.). Нечеткая математика: введение для инженеров и ученых . Физика. п. 2. ISBN 978-3-7908-1808-6 .
^ Танаев В.; Гордон, В.; Шафранский, Яков М. (6 декабря 2012 г.). Теория планирования. Одноступенчатые системы . Springer Science & Business Media. п. 41. ИСБН 978-94-011-1190-4 .
^ Мейер, Бертран (29 июня 2009 г.). Прикосновение к классу: учимся хорошо программировать с объектами и контрактами . Springer Science & Business Media. п. 509. ИСБН 978-3-540-92145-5 .
^ Фонсека де Оливейра, JN, и Перейра Кунья Родригес, CDJ (2004). Транспонирование отношений: от функций Maybe к хэш-таблицам . В «Математике построения программ» (с. 337).
^ Смит, Дуглас; Эгген, Морис; Сент-Андре, Ричард (2006), Переход к высшей математике (6-е изд.), Брукс/Коул, стр. 160, ISBN 0-534-39900-2
^ Нивергельт, Ив (2002), Основы логики и математики: приложения к информатике и криптографии , Springer-Verlag, стр. 158 .
^ Флашка, В.; Ежек, Дж.; Кепка, Т.; Кортелайнен, Дж. (2007). Транзитивные замыкания бинарных отношений I (PDF) . Прага: Школа математики – Физика Карлова университета. п. 1. Архивировано из оригинала (PDF) 2 ноября 2013 г. Лемма 1.1 (iv). Этот источник называет асимметричные отношения «строго антисимметричными».
^ Поскольку ни 5 не делит 3, ни 3 не делит 5, ни 3 = 5.
^ «Условие обоснованности» . ДоказательствоВики . Архивировано из оригинала 20 февраля 2019 года . Проверено 20 февраля 2019 г.
^ Фрайсс, Р. (15 декабря 2000 г.). Теория отношений, том 145 - 1-е издание (1-е изд.). Эльзевир. п. 46. ИСБН 9780444505422 . Проверено 20 февраля 2019 г.
^ Гюнтер Шмидт и Томас Стролейн (2012) [1987] Отношения и графики , стр. 54, в Google Книгах
^ Джозеф Г. Розенштейн, Линейные порядки , Academic Press, 1982, ISBN 0-12-597680-1 , с. 4
^ Шмидт, Гюнтер; Стрёлейн, Томас (1993). «Однородные отношения». Отношения и графики: дискретная математика для компьютерщиков . Берлин, Гейдельберг: Springer. п. 14. дои : 10.1007/978-3-642-77968-8_2 . ISBN 978-3-642-77968-8 .

[Winter2007-1] Майкл Винтер (2007). Категории Гогена: Категорический подход к L-нечетким отношениям . Спрингер. стр. x – xi. ISBN 978-1-4020-6164-6 .

[Müller2012-2] М. Е. Мюллер (2012). Открытие реляционных знаний . Издательство Кембриджского университета. п. 22. ISBN 978-0-521-19021-3 .

[PahlDamrath2001-p496-3] Питер Дж. Пал; Рудольф Дамрат (2001). Математические основы вычислительной техники: Справочник . Springer Science & Business Media. п. 496. ИСБН 978-3-540-67995-0 .

[4] Мордесон, Джон Н.; Наир, Премчанд С. (8 ноября 2012 г.). Нечеткая математика: введение для инженеров и ученых . Физика. п. 2. ISBN 978-3-7908-1808-6 .

[5] Танаев В.; Гордон, В.; Шафранский, Яков М. (6 декабря 2012 г.). Теория планирования. Одноступенчатые системы . Springer Science & Business Media. п. 41. ИСБН 978-94-011-1190-4 .

[6] Мейер, Бертран (29 июня 2009 г.). Прикосновение к классу: учимся хорошо программировать с объектами и контрактами . Springer Science & Business Media. п. 509. ИСБН 978-3-540-92145-5 .

[7] Фонсека де Оливейра, JN, и Перейра Кунья Родригес, CDJ (2004). Транспонирование отношений: от функций Maybe к хэш-таблицам . В «Математике построения программ» (с. 337).

[8] Смит, Дуглас; Эгген, Морис; Сент-Андре, Ричард (2006), Переход к высшей математике (6-е изд.), Брукс/Коул, стр. 160, ISBN 0-534-39900-2

[9] Нивергельт, Ив (2002), Основы логики и математики: приложения к информатике и криптографии , Springer-Verlag, стр. 158 .

[10] Флашка, В.; Ежек, Дж.; Кепка, Т.; Кортелайнен, Дж. (2007). Транзитивные замыкания бинарных отношений I (PDF) . Прага: Школа математики – Физика Карлова университета. п. 1. Архивировано из оригинала (PDF) 2 ноября 2013 г. Лемма 1.1 (iv). Этот источник называет асимметричные отношения «строго антисимметричными».

[11] Поскольку ни 5 не делит 3, ни 3 не делит 5, ни 3 = 5.

[12] «Условие обоснованности» . ДоказательствоВики . Архивировано из оригинала 20 февраля 2019 года . Проверено 20 февраля 2019 г.

[13] Фрайсс, Р. (15 декабря 2000 г.). Теория отношений, том 145 - 1-е издание (1-е изд.). Эльзевир. п. 46. ИСБН 9780444505422 . Проверено 20 февраля 2019 г.

[14] Гюнтер Шмидт и Томас Стролейн (2012) [1987] Отношения и графики , стр. 54, в Google Книгах

[15] Джозеф Г. Розенштейн, Линейные порядки , Academic Press, 1982, ISBN 0-12-597680-1 , с. 4

[16] Шмидт, Гюнтер; Стрёлейн, Томас (1993). «Однородные отношения». Отношения и графики: дискретная математика для компьютерщиков . Берлин, Гейдельберг: Springer. п. 14. дои : 10.1007/978-3-642-77968-8_2 . ISBN 978-3-642-77968-8 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]