Антиматроид

Три взгляда на антиматроид: порядок включения в его семействе допустимых множеств, формальный язык и соответствующее частичное упорядоченное множество путей.

В математике антиматроид . — это формальная система , описывающая процессы, в которых набор создается путем включения элементов по одному, и в которых элемент, однажды доступный для включения, остается доступным до тех пор, пока он не будет включен Антиматроиды обычно аксиоматизируются двумя эквивалентными способами : либо как система множеств, моделирующая возможные состояния такого процесса, либо как формальный язык, моделирующий различные последовательности, в которые могут быть включены элементы. Дилворт (1940) был первым, кто изучал антиматроидов, используя еще одну аксиоматизацию, основанную на теории решеток , и их часто переоткрывали в других контекстах.

Аксиомы, определяющие антиматроидов как системы множеств, очень похожи на аксиомы матроидов , но в то время как матроиды определяются аксиомой обмена , антиматроиды вместо этого определяются аксиомой антиобмена , от которой и происходит их название.Антиматроиды можно рассматривать как частный случай гридоидов и полумодулярных решеток , а также как обобщение частичных порядков и дистрибутивных решеток . Антиматроиды эквивалентны, путем дополнения , выпуклой геометрии , комбинаторной абстракции выпуклых множеств в геометрии .

Антиматроиды применялись для моделирования ограничений приоритета в задачах планирования , потенциальных последовательностей событий в симуляциях, планирования задач в искусственном интеллекте и состояний знаний обучающихся людей.

Определения

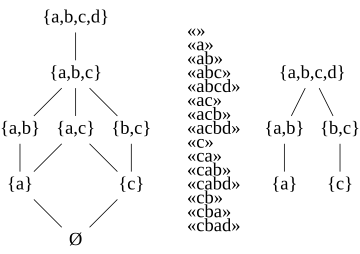
Антиматроид можно определить как конечное семейство ${\mathcal {F}}$ конечных множеств, называемых допустимыми множествами , со следующими двумя свойствами:

• Объединение любых двух допустимых множеств также возможно. То есть, ${\mathcal {F}}$ закрыт под профсоюзы.
• Если $S$ — непустое допустимое множество, то $S$ содержит элемент $x$ для чего $S\setminus \{x\}$ (множество, образованное удалением $x$ от $S$) тоже возможно. То есть, ${\mathcal {F}}$ представляет собой доступную систему множеств .

Антиматроиды также имеют эквивалентное определение как формальный язык , то есть как набор строк, определенных из конечного алфавита символов . Строка, принадлежащая этому множеству, называется словом языка. Язык ${\mathcal {L}}$ определение антиматроида должно удовлетворять следующим свойствам:

• Каждый символ алфавита встречается хотя бы в одном слове. ${\mathcal {L}}$.
• Каждое слово ${\mathcal {L}}$ содержит не более одной копии каждого символа. Язык, обладающий этим свойством, называется нормальным .
• Каждая приставка слова в ${\mathcal {L}}$ также находится в ${\mathcal {L}}$. Язык, обладающий этим свойством, называется наследственным .
• Если $S$ и $T$ это слова в ${\mathcal {L}}$, и $S$ содержит хотя бы один символ, которого нет в $T$, то есть символ $x$ в $S$ такое, что конкатенация $Tx$ это еще одно слово в ${\mathcal {L}}$.

Эквивалентность этих двух форм определения можно увидеть следующим образом. Если ${\mathcal {L}}$ — антиматроид, определенный как формальный язык, то наборы символов в словах ${\mathcal {L}}$ образуют доступную объединенно-замкнутую систему множеств. Доступ к нему осуществляется благодаря наследственному свойству строк, и можно показать, что он замкнут с помощью многократного применения свойства конкатенации строк. В другую сторону, от доступной союзно-замкнутой системы множеств. ${\mathcal {F}}$, язык обычных строк, все префиксы которого имеют наборы символов, принадлежащих ${\mathcal {F}}$ отвечает требованиям, предъявляемым к формальному языку, чтобы быть антиматроидом. Эти два преобразования являются обратными друг другу: преобразование формального языка в семейство множеств и обратно или наоборот создает одну и ту же систему. Таким образом, эти два определения приводят к математически эквивалентным классам объектов.

Примеры

Последовательность обстрела плоского множества точек. Отрезки линий показывают края выпуклых оболочек после удаления некоторых точек.

Следующие системы предоставляют примеры антиматроидов:

Цепные антиматроиды

Префиксы одной строки и наборы символов в этих префиксах образуют антиматроид. Например, цепочка антиматроидов определяется строкой $abcd$ формальным языком является набор строк

$$\{\varepsilon ,a,ab,abc,abcd\}$$

(где $\varepsilon$ обозначает пустую строку ) и в качестве ее семейства допустимых наборов используется семейство

$${\bigl \{}\emptyset ,\{a\},\{a,b\},\{a,b,c\},\{a,b,c,d\}{\bigr \}}.$$

Посет-антиматроиды

Нижние множества конечного частично упорядоченного множества образуют антиматроид, при этом полноразмерные слова антиматроида образуют линейные расширения частичного порядка. По теореме Биркгофа о представлении дистрибутивных решеток допустимые множества в антиматроиде частичного множества (упорядоченные по включению множеств) образуют дистрибутивную решетку, и все дистрибутивные решетки могут быть сформированы таким образом. Таким образом, антиматроиды можно рассматривать как обобщения дистрибутивных решеток. Цепной антиматроид — это частный случай частично-антиматроида полного порядка .

Обстрел антиматроидов

Последовательность обстрела конечного множества $U$ точек на евклидовой плоскости более высокой размерности или евклидовом пространстве формируется путем многократного удаления вершин выпуклой оболочки . Допустимые множества антиматроида, образованные этими последовательностями, пересечениями являются $U$ с дополнением выпуклого множества.

Идеальное устранение

Совершенный порядок исключения — хордального графа это такой порядок его вершин, что для каждой вершины $v$, соседи г. $v$ которые происходят позже, чем $v$ в форме заказа кликните . Префиксы совершенного порядка исключения хордального графа образуют антиматроид.

Чип-стреляющие игры

Игры со стрельбой фишками, такие как абелева модель песочницы, определяются ориентированным графом вместе с системой «фишек», размещенных в его вершинах. Всякий раз, когда количество фишек в вершине $v$ по крайней мере так же велико, как количество ребер из $v$, можно стрелять $v$, перемещая по одной фишке в каждую соседнюю вершину. Событие, которое $v$ пожары для $i$этот раз может произойти только в том случае, если он уже выстрелил $i-1$ раз и накоплено $i\cdot \deg(v)$ всего фишек. Эти условия не зависят от порядка предыдущих срабатываний и остаются верными до тех пор, пока $v$ срабатывает, поэтому любой заданный граф и начальное размещение фишек, при котором система завершает работу, определяет антиматроида на парах $(v,i)$. Следствием антиматроидного свойства этих систем является то, что для данного начального состояния количество срабатываний каждой вершины и конечное стабильное состояние системы не зависят от порядка срабатывания.

Пути и основные слова

В теоретико-множественной аксиоматизации антиматроида существуют определенные специальные множества, называемые путями , которые определяют весь антиматроид в том смысле, что множества антиматроида представляют собой в точности объединения путей. Если $S$ – любое допустимое множество антиматроида, элемент $x$ который можно удалить из $S$ для формирования другого допустимого множества, называется конечной точкой $S$, а допустимое множество, имеющее только один конец, называется путем антиматроида. Семейство путей можно частично упорядочить путем включения множества, образуя частичное множество путей антиматроида.

Для каждого допустимого множества $S$ в антиматроиде, и каждый элемент $x$ из $S$, можно найти подмножество пути $S$ для чего $x$ является конечной точкой: для этого удаляйте по одному элементы, кроме $x$ до тех пор, пока такое удаление не оставит допустимое подмножество. Следовательно, каждое допустимое множество в антиматроиде представляет собой объединение его подмножеств путей. Если $S$ не является путем, каждое подмножество в этом объединении является собственным подмножеством $S$. Но, если $S$ сам по себе является путем с конечной точкой $x$, каждое правильное подмножество $S$ принадлежащий антиматроиду, исключает $x$. Следовательно, пути антиматроида — это в точности допустимые множества, не равные объединениям своих собственных допустимых подмножеств. Эквивалентно, данное семейство множеств ${\mathcal {P}}$ образует семейство путей антиматроида тогда и только тогда, когда для каждого $S$ в ${\mathcal {P}}$, объединение подмножеств $S$ в ${\mathcal {P}}$ имеет на один элемент меньше, чем $S$ сам. Если так, ${\mathcal {F}}$ само по себе является семейством объединений подмножеств ${\mathcal {P}}$.

В формальной языковой формализации антиматроида самые длинные строки называются базовыми словами . Каждое основное слово образует перестановку всего алфавита. Если $B$ это набор основных слов, ${\mathcal {L}}$ можно определить из $B$ как набор префиксов слов в $B$.

Выпуклая геометрия

См. также: Выпуклое множество , Выпуклая геометрия и Оператор замыкания.

Если ${\mathcal {F}}$ - это система множеств, определяющая антиматроида, с $U$ равно объединению множеств в ${\mathcal {F}}$, то семейство множеств

$${\mathcal {G}}=\{U\setminus S\mid S\in {\mathcal {F}}\}$$

в дополнение к наборам в ${\mathcal {F}}$ иногда называют выпуклой геометрией , а множества в ${\mathcal {G}}$ называются выпуклыми множествами . Например, в антиматроиде-обстреле выпуклые множества являются пересечениями заданного множества точек с выпуклыми подмножествами евклидова пространства. Система множеств, определяющая выпуклую геометрию, должна быть замкнутой при пересечениях. Для любого набора $S$ в ${\mathcal {G}}$ это не равно $U$ должен быть элемент $x$ не в $S$ что можно добавить в $S$ чтобы сформировать еще один набор в ${\mathcal {G}}$.

Выпуклая геометрия также может быть определена с помощью оператора замыкания $\tau$ который отображает любое подмножество $U$ до своего минимального закрытого надмножества. Чтобы быть оператором замыкания, $\tau$ должен иметь следующие свойства:

• $\tau (\emptyset )=\emptyset$: замыкание пустого множества пусто.
• Для каждого подмножества $S$ из $U$, $S$ является подмножеством $\tau (S)$ и $\tau (S)=\tau {\bigl (}\tau (S){\bigr )}$.
• В любое время $S\subset T\subset U$, $\tau (S)$ является подмножеством $\tau (T)$.

Семейство замкнутых множеств, возникающее в результате операции замыкания этого типа, обязательно замкнуто относительно пересечений, но не может иметь выпуклую геометрию. Операторы замыкания, определяющие выпуклую геометрию, также удовлетворяют дополнительной аксиоме антиобмена :

• Если $S$ является подмножеством $U$, и $y$ и $z$ являются отдельными элементами $U$ которые не принадлежат $\tau (S)$, но $z$ принадлежит $\tau (S\cup \{y\})$, затем $y$ не принадлежит $\tau (S\cup \{z\})$.

Операция замыкания, удовлетворяющая этой аксиоме, называется антиобменным замыканием . Если $S$ является замкнутым множеством в антиобменном замыкании, то антиобменная аксиома определяет частичный порядок элементов, не принадлежащих $S$, где $x\leq y$ в частичном порядке, когда $x$ принадлежит $\tau (S\cup \{y\})$. Если $x$ является минимальным элементом этого частичного порядка, то $S\cup \{x\}$ закрыт. То есть семейство замкнутых множеств антиобменного замыкания обладает тем свойством, что для любого множества, отличного от универсального, существует элемент $x$ которые можно добавить к нему, чтобы создать еще один замкнутый набор. Это свойство дополняет свойство доступности антиматроидов, а тот факт, что пересечения замкнутых множеств замкнуты, дополняет свойство, согласно которому возможны объединения допустимых множеств в антиматроиде. Следовательно, дополнения к замкнутым множествам любого антиобменного замыкания образуют антиматроид.

в Неориентированные графы, которых выпуклые множества (подмножества вершин, содержащие все кратчайшие пути между вершинами в подмножестве) образуют выпуклую геометрию, являются в точности графами Птолемея .

Джойно-распределительные решетки

Любые два допустимых множества антиматроида имеют единственную наименьшую верхнюю границу (их объединение) и единственную наибольшую нижнюю границу (объединение множеств антиматроида, содержащихся в них обоих). Следовательно, допустимые множества антиматроида, частично упорядоченные включением множеств, образуют решетку . Различные важные особенности антиматроида можно интерпретировать в терминах теории решетки; например, пути антиматроида являются неприводимыми элементами соответствующей решетки, а основные слова антиматроида соответствуют максимальным цепям в решетке. Решетки, возникающие таким образом из антиматроидов, обобщают конечные дистрибутивные решетки и могут быть охарактеризованы несколькими различными способами.

• Описание, первоначально рассмотренное Дилвортом (1940), касается неприводимых элементов решетки. Для каждого элемента $x$ антиматроида существует единственное максимально допустимое множество $S_{x}$ который не содержит $x$: $S_{x}$ можно построить как объединение всех допустимых множеств, не содержащих $x$. Этот набор $S_{x}$ автоматически неприводимо, что означает, что он не является пересечением каких-либо двух более крупных элементов решетки. Это верно, потому что каждое возможное надмножество $S_{x}$ содержит $x$, и, следовательно, то же самое верно для каждого пересечения допустимых надмножеств. Каждый элемент произвольной решетки можно разложить как совокупность неприводимых множеств, часто несколькими способами, но в решетке, соответствующей антиматроиду, каждый элемент $T$ имеет единственное минимальное семейство встречающихся-неприводимых множеств, встреча которых $T$; это семейство состоит из наборов $S_{x}$ для элементов $x$ такой, что $T\cup \{x\}$ осуществимо. То есть решетка имеет единственные неприводимые разложения .
• Вторая характеристика касается интервалов в решетке, подрешеток, определяемых парой элементов решетки. $x\leq y$ состоящий из всех решетчатых элементов $z$ с $x\leq z\leq y$. Интервал является атомистическим , если каждый элемент в нем представляет собой объединение атомов (минимальные элементы над нижним элементом $x$), и оно является булевым , если оно изоморфно решетке всех подмножеств конечного множества. Для антиматроида каждый атомистический интервал также является логическим.
• В-третьих, решетки, возникающие из антиматроидов, являются полумодулярными решетками , решетками, удовлетворяющими верхнему полумодулярному закону , согласно которому для каждых двух элементов $x$ и $y$, если $y$ обложки $x\wedge y$ затем $x\vee y$ обложки $x$. Переводя это условие в допустимые множества антиматроида, если допустимое множество $Y$ имеет только один элемент, не принадлежащий другому допустимому множеству $X$ тогда этот один элемент может быть добавлен к $X$ чтобы сформировать еще один набор в антиматроиде. Кроме того, решетка антиматроида обладает свойством встречи-полудистрибутивности : для всех элементов решетки $x$, $y$, и $z$, если $x\wedge y$ и $x\wedge z$ равны друг другу, то они также оба равны $x\wedge (y\vee z)$. Полумодулярная и встречно-полудистрибутивная решетка называется присоединенно-дистрибутивной решеткой .

Эти три характеристики эквивалентны: любая решетка с уникальными неприводимыми разложениями имеет булевы атомистические интервалы и является дистрибутивной по соединению; встречаются неприводимые разложения и булевы атомистические интервалы. Таким образом, мы можем называть решетку с любым из этих трех свойств соединительно-дистрибутивной. Любой антиматроид порождает конечную присоединительно-дистрибутивную решетку, и таким образом любая конечная соединительно-дистрибутивная решетка возникает из антиматроида. Другая эквивалентная характеристика конечных объединенно-дистрибутивных решеток состоит в том, что они градуированы (любые две максимальные цепи имеют одинаковую длину), а длина максимальной цепи равна числу встречно-неприводимых элементов решетки. Антиматроид, представляющий конечную соединительно-дистрибутивную решетку, может быть восстановлен из решетки: элементами антиматроида можно считать встречающиеся неприводимые элементы решетки, а допустимое множество, соответствующее любому элементу $x$ решетки состоит из множества встречающихся неприводимых элементов $y$ такой, что $y$ не больше или равно $x$ в решетке.

Это представление любой конечной присоединяюще-дистрибутивной решетки как доступного семейства множеств, замкнутых относительно объединений (то есть как антиматроида), можно рассматривать как аналог теоремы Биркгофа о представлении , согласно которой любая конечная дистрибутивная решетка имеет представление в виде семейства множеств закрытые под объединениями и пересечениями.

Сверхразрешимые антиматроиды

Руководствуясь проблемой определения частичных порядков элементов группы Кокстера , Армстронг (2009) изучал антиматроиды, которые также являются сверхразрешимыми решетками . Сверхразрешимый антиматроид определяется полностью упорядоченным набором элементов и семейством множеств этих элементов. Семья должна включать пустой набор. Кроме того, оно должно обладать свойством, что если два множества $A$ и $B$ принадлежат семейству, если теоретико -множественная разность $B\setminus A$ непусто, и если $x$ является наименьшим элементом $B\setminus A$, затем $A\cup \{x\}$ тоже принадлежит семье. Как отмечает Армстронг, любое семейство множеств этого типа образует антиматроид. Армстронг также дает теоретико-решеточную характеристику антиматроидов, которые может образовать эта конструкция.

Операция соединения и выпуклое измерение

Если ${\mathcal {A}}$ и ${\mathcal {B}}$ — это два антиматроида, оба описываемые как семейство множеств в одной и той же вселенной элементов, затем другой антиматроид соединение , ${\mathcal {A}}$ и ${\mathcal {B}}$, можно сформировать следующим образом:

$${\mathcal {A}}\vee {\mathcal {B}}=\{S\cup T\mid S\in {\mathcal {A}}\wedge T\in {\mathcal {B}}\}.$$

Это операция, отличная от операции соединения, рассматриваемой в теоретико-решеточных характеристиках антиматроидов: она объединяет два антиматроида для формирования другого антиматроида, а не объединяет два набора в антиматроид для формирования другого набора. С помощью этой операции соединения семейство всех антиматроидов в одной вселенной образует полурешетку .

Соединения тесно связаны с операцией замыкания, которая сопоставляет формальные языки с антиматроидами, где замыкание языка ${\mathcal {L}}$ является пересечением всех антиматроидов, содержащих ${\mathcal {L}}$ как подъязык. Это замыкание имеет в качестве возможных наборов объединения префиксов строк в ${\mathcal {L}}$. С точки зрения этой операции замыкания соединение представляет собой замыкание объединения языков ${\mathcal {A}}$ и ${\mathcal {B}}$. Каждый антиматроид может быть представлен как объединение семейства цепных антиматроидов или, что то же самое, как замыкание набора основных слов; выпуклое измерение антиматроида ${\mathcal {A}}$ — минимальное количество цепных антиматроидов (или, что то же самое, минимальное количество основных слов) в таком представлении. Если ${\mathfrak {F}}$ это семейство цепных антиматроидов, все основные слова которых принадлежат ${\mathcal {A}}$, затем ${\mathfrak {F}}$ генерирует ${\mathcal {A}}$ тогда и только тогда, когда допустимые множества ${\mathfrak {F}}$ включить все пути ${\mathcal {A}}$. Пути ${\mathcal {A}}$ принадлежащий одному цепному антиматроиду, должен образовывать цепочку в частичном множестве путей ${\mathcal {A}}$, поэтому выпуклая размерность антиматроида равна минимальному количеству цепей, необходимых для покрытия частичного набора путей, что по теореме Дилворта равно ширине частичного набора путей.

Если иметь представление антиматроида как замыкание множества $d$ Если говорить базовыми словами, то это представление можно использовать для отображения допустимых множеств антиматроида в точки в $d$-мерное евклидово пространство: назначьте одну координату каждому базовому слову. $W$и сделаем значение координаты допустимого множества $S$ быть длиной самого длинного префикса $W$ это подмножество $S$. Благодаря этому вложению $S$ является подмножеством другого допустимого множества $T$ тогда и только тогда, когда координаты $S$ все меньше или равны соответствующим координатам $T$. Поэтому порядковая размерность порядка включения допустимых множеств не более чем равна выпуклой размерности антиматроида. Однако в общем случае эти два измерения могут сильно различаться: существуют антиматроиды с размерностью три, но со сколь угодно большой выпуклой размерностью.

Перечисление

Число возможных антиматроидов в наборе элементов быстро растет с увеличением количества элементов в наборе. Для множеств из одного, двух, трех и т. д. элементов число различных антиматроидов равно

$$1,3,22,485,59386,133059751,\dots \,.$$

Приложения

И ограничения приоритета, и время выпуска в стандартных обозначениях теоретических задач планирования могут моделироваться с помощью антиматроидов. Бойд и Фейгл (1990) используют антиматроиды для обобщения жадного алгоритма Юджина Лоулера для оптимального решения задач однопроцессорного планирования с ограничениями приоритета, цель которых состоит в том, чтобы минимизировать максимальный штраф, наносимый поздним планированием задачи.

Глассерман и Яо (1994) используют антиматроидов для моделирования порядка событий в системах моделирования дискретных событий .

Пармар (2003) использует антиматроидов для моделирования прогресса на пути к цели в искусственного интеллекта задачах планирования .

В Теории Оптимальности , математической модели развития естественного языка, основанной на оптимизации при ограничениях, грамматики логически эквивалентны антиматроидам.

В математической психологии антиматроиды использовались для описания возможных состояний знаний обучающегося человека. Каждый элемент антиматроида представляет собой концепцию, которую должен понять учащийся, или класс задач, которые он или она может правильно решить, а наборы элементов, образующих антиматроид, представляют собой возможные наборы концепций, которые могут быть решены правильно. понятен одному человеку. Аксиомы, определяющие антиматроида, можно неформально сформулировать как утверждение, что изучение одной концепции никогда не может помешать учащемуся изучить другую концепцию и что любого возможного уровня знаний можно достичь, изучая одну концепцию за раз. Задача системы оценки знаний состоит в том, чтобы сделать вывод о наборе понятий, известных данному учащемуся, путем анализа его или ее ответов на небольшой и хорошо выбранный набор проблем. В этом контексте антиматроидов также называют «пространствами обучения» и «пространствами хорошо оцененных знаний».

Ссылки

• Адаричева, К.В.; Горбунов В.А.; Туманов В.И. (2003), «Соединительно-полураспределительные решетки и выпуклые геометрии», Успехи математики , 173 (1): 1–49, doi : 10.1016/S0001-8708(02)00011-7 .
• Армстронг, Дрю (2009), «Порядок сортировки группы Кокстера», Журнал комбинаторной теории , серия A, 116 (8): 1285–1305, arXiv : 0712.1047 , doi : 10.1016/j.jcta.2009.03.009 , МР   2568800 , S2CID   15474840 .
• Биркгоф, Гарретт ; Беннетт, М.К. (1985), «Решетка выпуклости частичного множества» , Order , 2 (3): 223–242, doi : 10.1007/BF00333128 , S2CID   118907732
• Бьёрнер, Андерс ; Ловас, Ласло ; Шор, Питер В. (1991), «Игры со стрельбой чипами на графах», European Journal of Combinatorics , 12 (4): 283–291, doi : 10.1016/S0195-6698(13)80111-4 , MR   1120415
• Бьёрнер, Андерс ; Циглер, Гюнтер М. (1992), «Введение в гридоиды» , в книге Уайт, Нил (редактор), «Приложения Матроида» , Энциклопедия математики и ее приложений, том. 40, Кембридж: Издательство Кембриджского университета, стр. 284–357 , номер документа : 10.1017/CBO9780511662041.009 , ISBN.  0-521-38165-7 , МР   1165537
• Бойд, Э. Эндрю; Фейгл, Ульрих (1990), «Алгоритмическая характеристика антиматроидов», Discrete Applied Mathematics , 28 (3): 197–205, doi : 10.1016/0166-218X(90)90002-T , hdl : 1911/101636 .
• Чандран, Л.С.; Ибарра, Л.; Раски, Ф .; Савада, Дж. (2003), «Генерация и характеристика идеального порядка исключения хордального графа» (PDF) , Theoretical Computer Science , 307 (2): 303–317, doi : 10.1016/S0304-3975(03)00221- 4
• Дилворт, Роберт П. (1940), «Решетки с уникальными неприводимыми разложениями», Annals of Mathematics , 41 (4): 771–777, doi : 10.2307/1968857 , JSTOR   1968857 .
• Дуаньон, Жан-Поль; Фальмань, Жан-Клод (1999), Пространства знаний , Springer-Verlag, ISBN  3-540-64501-2 .
• Эдельман, Пол Х. (1980), «Встреча-распределительные решетки и антиобменное замыкание», Algebra Universalis , 10 (1): 290–299, doi : 10.1007/BF02482912 , S2CID   120403229 .
• Эдельман, Пол Х.; Сакс, Майкл Э. (1988), «Комбинаторное представление и выпуклая размерность выпуклых геометрий», Order , 5 (1): 23–32, doi : 10.1007/BF00143895 , S2CID   119826035 .
• Эппштейн, Дэвид (2008), Последовательности обучения , arXiv : 0803.4030 . Частично адаптировано как главы 13 и 14 Фальмань, Жан Клод ; Альберт, Дитрих; Добл, Крис; Эппштейн, Дэвид ; Ху, Сянген, ред. (2013), Пространства знаний: приложения в образовании , Springer-Verlag, doi : 10.1007/978-3-642-35329-1 , ISBN  978-3-642-35328-4 .
• Фарбер, Мартин; Джеймисон, Роберт Э. (1986), «Выпуклость в графах и гиперграфах», SIAM Journal on Algebraic and Discrete Methods , 7 (3): 433–444, doi : 10.1137/0607049 , hdl : 10338.dmlcz/127659 , MR   0844046 .
• Глассерман, Пол; Яо, Дэвид Д. (1994), Монотонная структура в дискретных системах событий , Ряды Уайли по вероятности и статистике, Wiley Interscience, ISBN  978-0-471-58041-6 .
• Гордон, Гэри (1997), «β-инвариант для гридоидов и антиматроидов», Electronic Journal of Combinatorics , 4 (1): Research Paper 13, doi : 10.37236/1298 , MR   1445628 .
• Джеймисон, Роберт (1980), «Коточки в антиматроидах», Труды одиннадцатой Юго-восточной конференции по комбинаторике, теории графов и вычислениям (Флоридский Атлантический университет, Бока-Ратон, Флорида, 1980), Vol. II , Конгресс Нумерантиум, том. 29, стр. 535–544, МР   0608454 .
• Кемпнер, Юлия; Левит, Вадим Э. (2003), «Соответствие между двумя антиматроидными алгоритмическими характеристиками» , Электронный журнал комбинаторики , 10 : Исследовательская статья 44, arXiv : math/0307013 , Bibcode : 2003math......7013K , doi : 10.37236/ 1737 , МР   2014531 , С2КИД   11015967
• Кнауэр, Коля (2009), «Выстрел чипов, антиматроиды и многогранники», Европейская конференция по комбинаторике, теории графов и приложениям (EuroComb 2009) , Электронные заметки по дискретной математике, том. 34, стр. 9–13, doi : 10.1016/j.endm.2009.07.002 , MR   2591410
• Корте, Бернхард ; Ловас, Ласло ; Шрейдер, Райнер (1991), Greedoids , Springer-Verlag, стр. 19–43, ISBN  3-540-18190-3 .
• Купец, Назарре; Риггл, Джейсон (2016), «OT-грамматики, помимо частичных порядков: наборы ERC и антиматроиды» , Natural Language & Linguistic Theory , 34 : 241–269, doi : 10.1007/s11049-015-9297-5 , S2CID   170567540 .
• Монжарде, Бернар (1985), «Использование для частого повторного открытия концепции», Order , 1 (4): 415–417, doi : 10.1007/BF00582748 , S2CID   119378521 .
• Пармар, Аарати (2003), «Некоторые математические структуры, лежащие в основе эффективного планирования», Весенний симпозиум AAAI по логической формализации рассуждений здравого смысла (PDF) .