Измерение объема дерева

Объем дерева — один из многих параметров, которые измеряются для определения размера отдельных деревьев. Измерение объема деревьев служит различным целям: экономическим, научным и спортивным. Измерения могут включать только объем ствола или объем ствола и ветвей в зависимости от необходимой детализации и сложности методологии измерения.

Другие часто используемые параметры, описанные в разделе «Измерение дерева» : измерение высоты дерева , измерение обхвата дерева и измерение кроны дерева . Измерения объема могут быть выполнены с помощью альпинистов, производящих прямые измерения, или дистанционными методами. В каждом методе дерево разбивается на более мелкие секции, измеряются размеры каждой секции и рассчитывается соответствующий объем. Затем объемы секций суммируются для определения общего объема дерева или части моделируемого дерева. В общем, большинство секций рассматриваются как усеченные конусы на каждом конце и , параболоиды или нейлоиды, где диаметр длина каждой секции определяются для расчета объема . Прямые измерения производятся альпинистом, который с помощью рулетки измеряет обхват на каждом конце сегмента и его длину. Наземные методы используют оптическое и электронное геодезическое оборудование для дистанционного измерения концевых диаметров и длины каждой секции.

Самые большие деревья в мире по объему — это гигантские секвойи в национальном парке Кингс-Каньон . Ранее по объему багажника они сообщались как: General Sherman - 52 508 кубических футов (1 486,9 м 3). ³ ); Генерал Грант в 46 608 кубических футов (1319,8 м ³ ); и Президент - 45 148 кубических футов (1 278,4 м ³ ). Самая большая негигантская секвойя, стоящая в настоящее время, «Потерянный монарх», имеет площадь 42 500 кубических футов (1 203,5 м 2 ). ³ ), крупнее всех, кроме пяти крупнейших ныне живущих гигантских секвой. « Потерянный монарх» — это прибрежное красное дерево (Sequoia sempervirens) в Северной Калифорнии, диаметром 26 футов (7,9 м) на высоте груди (с несколькими стеблями) и высотой 320 футов (98 м). В 2012 году группа исследователей под руководством Стивена Силлетта составила подробную карту ветвей президентского дерева и рассчитала, что объем ветвей составляет 9000 кубических футов (250 м3). ³ ). Это увеличит общий объем для президента с 45 000 кубических футов до 54 000 кубических футов (1500 м3). ³ ), превосходящий объем Общего дерева грантов. Объем ветвей деревьев Генерала Гранта и Генерала Шермана еще предстоит измерить в таких деталях.

Прямые измерения объема – багажник

Альпинисты по деревьям могут физически измерить высоту и окружность дерева с помощью рулетки. Расстояние от самой высокой точки подъема и вершины дерева измеряется с помощью шеста, который проходит от вершины дерева до точки крепления ленты. Отмечают эту высоту и в этой точке измеряют диаметр дерева. Затем альпинист спускается по дереву, измеряя окружность ствола с помощью ленты, обмотанной на разной высоте, причем высота каждого измерения относится к фиксированной ленте, проходящей по стволу.

Прямые измерения ствола производятся альпинистом. Альпинист будет подниматься на дерево до тех пор, пока не достигнет самой высокой безопасной точки лазания. Достигнув этой точки, альпинист бросает утяжеленную веревку прямо на землю. Затем измерительную (эталонную) ленту прикрепляют с помощью небольшого карабина к сброшенной веревке броска и тянут вверх, следуя вертикальной траектории падения гири. На этом этапе лента прикрепляется к стволу с помощью нескольких канцелярских кнопок и может свободно свисать по стволу. Отмечается точное положение прихватки относительно верхушки дерева. Если до вершины дерева невозможно было безопасно добраться, для измерения оставшегося расстояния до самой высокой точки дерева используется шест или палка.

Измерение верхушки дерева

Альпинист поднимает выдвижной шест и использует его, чтобы добраться до вершины дерева из точки на верхнем конце ленты. Если он не вертикальный, измеряется наклон наклонной опоры и измеряется длина опоры. Расстояние по вертикали, добавляемое вехой к длине ленты, равно (sin Θ x длина вехи). Нижний конец ленты заканчивается у основания дерева. На склоне это точка середины уклона между самой низкой и самой высокой сторонами дерева. Общая высота дерева равна измеренному расстоянию от основания на середине уклона до верхнего конца ленты, прикрепленной к дереву, плюс вертикальная высота, измеренная до фактической вершины дерева. Измерения обхвата производятся путем обматывания ленты вокруг дерева перпендикулярно стволу через последовательные промежутки времени, когда альпинист спускается по дереву. Все точки измерения привязаны к высоте над землей, измеренной на фиксированной эталонной ленте. Интервалы измерений выбираются субъективно, исходя из изменения конусности ствола. Область, где наблюдается изменение профиля (внутри или наружу), измеряется рулеткой. Свободные участки ствола выбираются так, чтобы не было воротников ветвей, капа и т. д. Для наибольшей точности измерения проводятся на одноствольных деревьях с интервалом не более 10 футов (3 м). Дополнительные измерения обычно требуются в тех случаях, когда ствол разветвляется или раздваивается, а также в случае повторения ствола .

Повторения идентифицируются по перевернутой ветви, которая приобрела апикальное доминирование и образовала дополнительную ветвь, поддерживающую ствол. Длина повторения завершается в точке контакта магистрали. Повторения ствола измеряются и добавляются к окончательному объему ствола. Бифуркация определяется как расщепление или развилка ствола, которая образует два или чаще восходящих ствола одинакового размера. Бифуркации часто образуют сплавленный участок неправильной формы, который невозможно точно измерить рулеткой с целью расчета площади поперечного сечения. Все длины бифуркаций заканчиваются в предполагаемом месте отхождения сердцевины от основного стержня.

Отображение кадров

В рамках проекта Tsuga Search Project была разработана методика картирования кадров, позволяющая охарактеризовать значительно большие области слияния на развилках деревьев. С двумя альпинистами, каждый из которых находится на противоположных сторонах дерева, выбирается область слияния для измерения. Два шеста, длиннее диаметра сваренной секции, поднимаются на место и соединяются тонкой веревкой, продетой через противоположные концы, чтобы их можно было регулировать. Шесты временно натягивают и измеряют расстояние между концами. Регулировки производятся до тех пор, пока они не станут параллельными и перпендикулярными оси туловища. Небольшое натяжение между шестами удерживает их устойчиво к стволу. Колья палатки, вклиненные в кору, также можно использовать для выравнивания и устойчивости каркаса. Один конец обозначен как ось Y, а прилегающая сторона — как ось X. С помощью столярной ленты производятся замеры от рамы до края ствола и чертится профиль формы ствола. Затем данные вводятся в функцию площади трапеции в электронной таблице и преобразуются в площадь поперечного сечения, чтобы вычислить эквивалентную длину окружности для использования в формуле объема.

Картирование следов

Многие деревья значительно расширяются наружу у основания, и этот базальный клин имеет сложную поверхность из неровностей и впадин. У деревьев, растущих на склоне, объем становится еще более сложным. Во многих случаях можно использовать аппроксимацию объема этого базального сегмента с использованием наилучших оценок показанного эффективного диаметра. В других случаях возможно картирование контуров. При картографировании контуров уровень прямоугольной системы отсчета размещается вокруг основания дерева, чтобы создать горизонтальную плоскость. Положение нескольких точек на поверхности туловища измеряется относительно рамы и наносится на график. Этот процесс повторялся на разной высоте, создавая серию виртуальных срезов на разной высоте. Затем рассчитывается объем каждого отдельного среза, и все они суммируются для определения объема базального клина.

Удаленные измерения объема – багажник

Дистанционные измерения объема ствола обычно производятся с места на земле, где наблюдатель имеет четкое представление о всей длине ствола. Измерения могут проводиться с использованием профессионального геодезического оборудования, такого как тахеометр или такой инструмент, как Criterion RD1000, с использованием комбинации монокуляра с сеткой, лазерным дальномером и клинометром , с использованием фотографических методов в сочетании с лазерным дальномером и клинометром, или с использованием картографирования облаков методов .

Электронные геодезические инструменты, такие как тахеометр, позволяют наблюдателю измерять положение каждого измерения диаметра и длину секции ствола между каждым измерением. У большинства инструментов диаметр определяется путем измерения угла азимута между противоположными сторонами ствола. Измеренные лазером расстояния до сторон ствола, представляющие концы диаметра и прилежащий угол, используются в соответствии с законом косинусов для расчета диаметра. Criterion RD 1000 имеет специальную функцию, позволяющую измерять диаметр с помощью видимого дисплея. Эти значения длины и диаметра затем можно использовать для определения объема отдельной секции.

Другой метод доступен для тех, у кого есть инструменты для измерения горизонтальных углов. На следующей схеме показано, как измерить диаметр дистанционно с помощью лазерного дальномера для измерения расстояния до середины ствола и транзита, компаса или другого устройства для измерения горизонтального угла, создаваемого диаметром. Обратите внимание, что в этом методе измеритель измеряет середину ствола, а не край. Кроме того, полный диаметр не обязательно должен быть виден с точки измерения. Распространено заблуждение, что более близкие расстояния приводят к ошибкам, поскольку измеритель не может видеть весь диаметр. Однако, если ствол круглый, близость не имеет значения. На схеме d = диаметр, D = расстояние от мерителя до середины дерева, а = угол от середины до края ствола. Вариант этого метода состоит в том, чтобы измерить полный угол, занимаемый изображением ствола, и разделить его на 2, чтобы получить угол a .

Измерение диаметра ствола

Комбинация монокуляра с сеткой, лазерного дальномера и клинометра. может использоваться для перехода от простых диаметров к полному измерению объема ствола. Монокуляр с сеткой — это небольшой телескоп, внутренняя шкала которого видна через стекло. Монокуляр устанавливают на штатив и рассматривают ствол дерева через монокуляр. Ширина ствола измеряется во многих единицах шкалы сетки . Высота над или расстояние под инструментом и расстояние до целевой точки измеряются с помощью лазерного дальномера и клинометра. Расстояние измеряется до центра (стороны) дерева. Зная известное расстояние, можно рассчитать измеренный диаметр дерева, выраженный в единицах шкалы сетки, и оптический коэффициент масштабирования для монокуляра с сеткой, определяемый диаметром дерева в этой точке:

диаметр = (масштаб сетки) × (расстояние до цели) ÷ (оптический коэффициент)

Для обеспечения точности калибровку оптического коэффициента следует проверять для каждого прибора, а не полагаться исключительно на спецификации производителя.

С помощью этой процедуры систематически измеряют ряд диаметров дерева вверх по стволу от основания дерева до вершины и отмечают их высоту. Иногда диаметр можно измерить с помощью монокуляра с сеткой на участках, где трудно получить точные лазерные расстояния из-за промежуточных тонких кустов или ветвей. Расстояния до затененного участка могут быть интерполированы на основе измерений, выполненных выше и ниже затененного участка.

Разрабатываются некоторые фотографические методы, позволяющие рассчитывать диаметры сегментов туловища и конечностей на фотографиях, содержащих масштаб известного размера и расстояние до цели. По сути, камера рассматривается как монокуляр с сеткой, и «оптический коэффициент» для камеры с определенным фокусным расстоянием рассчитывается для каждой фотографии на основе размера эталонной шкалы и ее расстояния от камеры. Масштаб не обязательно должен присутствовать на каждом изображении отдельного дерева, если фокусное расстояние не менялось между изображениями. Используя этот принцип, можно сделать снимок каждой точки измерения через увеличенное изображение, чтобы сделать измерения обхвата более простыми и точными. Кроме того, это позволяет использовать для измерений центральную, менее оптически искаженную часть изображения. Измеренный диаметр почти цилиндрической секции не будет существенно меняться в зависимости от угла обзора. Используя данные клинометра и измерений расстояний на каждом конце сегмента, можно рассчитать высоту, длину и расстояние между промежуточными точками, а также измерить диаметры ствола в этих точках. Одним из преимуществ фотографического метода является повсеместное распространение цифровой камеры . Кроме того, как только данные каркаса будут измерены в полевых условиях, процесс измерения диаметра ствола можно будет выполнить позже на компьютере . Фотоизображение также можно легко измерить повторно, если в расчетах обнаружена ошибка.

Картирование облаков точек — это процесс, разрабатываемый Майклом Тейлором. с использованием технологии оптического параллаксного сканирования, при которой вокруг ствола дерева проводятся тысячи измерений. Их можно использовать для воссоздания трехмерной модели багажника, а данные об объеме входят в число значений, которые можно рассчитать. Существует несколько широко доступных технологий, включая наземный лидар и оптические сканеры параллакса, которые могут быстро и точно составить карту ствола. У ЛИДАРа лучший диапазон. Проблема в том, что в захламленной лесной среде вы получаете много «шума» и нежелательных точек облаков, потенциально сотни тысяч, но их можно отфильтровать. Поверхность стволов деревьев можно нанести на карту с помощью оптического сканера, который измеряет коэффициент смещения пикселей между фокусным центром цифровой камеры и проекцией линейного лазера и смешивает его с данными пикселей фотографии. Тейлор сообщает эти оптические данные можно дополнить с помощью такой системы, как лазер Impulse200LR и программного обеспечения Mapsmart. для нацеливания на труднодоступные районы, где плотность облаков низкая и/или недостижимая с помощью технологии оптического сканирования, при условии, что сначала будет создана правильно масштабированная скелетная структура с помощью комбинации MapSmart/Impulse200. Данные можно сохранить в виде файла .ply, который можно просматривать и манипулировать с помощью различных программных пакетов, включая бесплатную программу просмотра 3D-графики с открытым исходным кодом Meshlab. Существует несколько доступных программ, которые можно использовать для расчета объема пространства, определенного облаком точек, включая некоторое дерево, которое в настоящее время находится в стадии разработки.

В настоящее время с использованием технологии картографирования облаков точек успешно нанесено на карту только нижние части стволов деревьев, но оцениваются различные варианты картирования всей длины ствола этих деревьев. Картирование основания этих деревьев облаком точек может быстро создать трехмерное представление основания этих больших деревьев с гораздо большей детализацией, чем это можно практически получить с помощью традиционного картографирования контуров.

Измерение объема конечностей и ветвей

Объемы конечностей и ветвей представляют собой серьезные проблемы. Необходимо не только измерить обхваты каждого конца сегмента ветки, но и определить длину сегмента конечности для конечностей, ориентированных в разные стороны. Собранная информация должна быть дополнительно организована таким образом, чтобы гарантировать, что каждый раздел был измерен и ни один из участков не измерялся дважды. Измерения длины и диаметра конечностей могут быть выполнены альпинистами, измеряющими эти значения физически, или дистанционными методами, или комбинацией того и другого. В большинстве случаев диаметры ветвей измеряются только до определенного нижнего предела размера, а объем остальных более тонких ветвей игнорируется или экстраполируется.

Объем конечностей и ветвей может быть значительным. Например, было обнаружено, что дуб Миддлтон Лайв ( Quercus Virginiana ) высотой 67,4 фута, глубиной 10,44 фута, шириной кроны 118 футов) имеет объем ствола 970 футов. ³ (24,5 м ³ ) и объемом ветки 3850 футов. ³ (109 м ³ ) Объем ветки почти в 4 раза превышал объем ствола. В отличие от этого, тюльпановое дерево Sag Branch ( Liriodendron tulipifera ) высотой 167,7 футов, высотой 7,08 футов, шириной кроны 101 фут) имело объем ствола 2430 футов. ³ (68,6 м ³ ) и объемом ветки 1560 футов. ³ (44,17 м ³ ). Объем ветвей тюльпанного дерева составлял всего 64,2% от объема ствола. Президентское дерево (Sequoiadendron giganteum) [3] было измерено в 2012 году и имело объем ствола 54 000 кубических футов (1500 м²). ³ ) древесины и ветки объемом 9000 кубических футов (250 м3). ³ ) древесины в ветвях. У этого гигантского дерева объем ветвей составлял всего 16,7% от объема ствола. У многих деревьев с меньшими или меньшим количеством крупных ветвей объем ветвей может составлять в среднем всего 5–10% объема ствола.

Для важных экземпляров можно выполнить детальное трехмерное картографирование ствола и основных ветвей деревьев. Методология, используемая для картирования дуба Миддлтон и тюльпана Саг-Ветвь, была разработана доктором Робертом Ван Пелтом . Этот процесс называется картографированием навеса . Его можно использовать для измерения объема ветвей внутри самого дерева для исключений или сложных деревьев. Измерения на земле также можно проводить там, где ветви можно адекватно проследить в кроне дерева.

Картографирование навеса

Картирование навеса — это процесс, при котором положение и размер ветвей внутри навеса наносятся на карту в трехмерном пространстве. Это трудоемкий процесс, который обычно применяется только к наиболее важным образцам. Обычно это делается из заданной позиции или серии позиций в дереве. Для облегчения процесса используются эскизы и фотографии. Лазают по деревьям и наносят на карту общую архитектуру, включая расположение главного ствола и всех повторяющихся стволов, а также всех ветвей, исходящих от стволов. Также наносится на карту положение каждой точки ветвления в кроне до определенного размера, а также положения различных повторений, разрывов, изломов или любых других эксцентриситетов в дереве. У каждого нанесенного на карту ствола и ветви измеряются базальный диаметр, длина и азимут. Альпинисты измеряют конкретные окружности и другие особенности дерева.

Ван Пелт и др. (2004) описал этот процесс в книге «Количественная оценка и визуализация структуры полога высоких лесов: методы и тематическое исследование». В этом примере он использовал лазерный прибор LTI Criterion 400 для картирования крон деревьев. По сути, это устройство, включающее в себя лазерный дальномер, клинометр и компас. LTI Criterion 400 использует инфракрасный полупроводниковый лазерный диод для измерения наклонного расстояния. Вертикальный энкодер, чувствительный к наклону, обеспечивает вертикальный наклон, а феррозондовый электронный компас измеряет магнитный азимут, дополняя данные, необходимые для определения трехмерного местоположения точки в пространстве. Он используется для отображения положения каждой точки ветвления в кроне до определенного размера, а также положения различных повторений, разрывов, изломов или любых других эксцентриситетов в дереве. Обычно это делается из заданной позиции или серии позиций в дереве. Для облегчения процесса используются эскизы и фотографии. Были залезли на деревья и нанесли на карту архитектуру в соответствии с ранее установленными критериями. Это включает в себя картирование местоположения главного ствола и всех повторяющихся стволов, а также всех ветвей, исходящих от стволов. Для каждого нанесенного на карту ствола и ветви были измерены базальный диаметр, длина, азимут. Альпинисты измеряют определенные окружности и детализируют другие особенности дерева. Кроме того, составляется карта следов основания дерева для расчета точного объема базальной части дерева. Данные обрабатываются в Excel для расчета объема. Графические функции можно использовать для создания трехмерной фигуры данных дерева. Доктор Ван Пелт также использует макрос Excel для поворота изображения, чтобы его можно было рассматривать под разными углами. В случае с тюльпаном Middleton Live Oak и Sag Branch каждое дерево было нанесено на карту с одной заданной станции из-под кроны каждого дерева.

Наземные измерения

Наземные измерения могут использоваться для дистанционного измерения длины конечностей и диаметров секций ветвей с помощью монокуляра с сеткой или фотографического анализа. Если сам ствол отклонен от вертикали, необходимо провести дополнительные измерения, чтобы определить истинную длину каждого сегмента ствола, а не просто рассматривать его как вертикальную колонну. Длину сегмента можно определить путем измерения положения конечных точек ветки в трехмерном пространстве от внешней исходной позиции. Затем длина вычисляется с применением теоремы Пифагора. Следующая диаграмма иллюстрирует этот процесс.

Трехмерные координатные расчеты

Из внешней опорной позиции O прямое расстояние до L ₁ измеряется до P ₁ вместе с вертикальным углом V ₁ и азимутом A ₁ . координаты x ₁ , y ₁ и z ₁ Затем вычисляются . Тот же процесс повторяется для P ₂ .Данная последовательность осуществляется следующим образом:Горизонтальное расстояние d ₁ от начальной контрольной точки O до целевой точки P ₁ вычисляется как d ₁ = cos(наклон) × лазерное расстояние = L ₁ sin V ₁ Значение x в первой точке равно: x ₁ = sin(азимут) × горизонтальное расстояние = d ₁ sin A ₁ Значение y в первой точке равно: y ₁ = cos(азимут) × горизонтальное расстояние = d ₁ cos A ₁ Значение z в первой точке равно: z ₁ = sin(наклон) × расстояние лазера = L ₁ sin V ₁ Этот процесс повторяется для P ₂ , чтобы получить x ₂ , y ₂ , z ₂ .Последний шаг — вычислить расстояние от P ₁ до P ₁ ( L ), используя следующую формулу.

$L={\sqrt {(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}+(z_{2}-z_{1})^{2}}}$

Обратите внимание, что вычисление включает в себя возведение в квадрат изменений значений x , y и z , сложение этих квадратов и извлечение квадратного корня из суммы.

Леверетт разработала методологию, согласно которой длина конечности измеряется с помощью монокуляра с сеткой, ориентированной вдоль ориентации конечности, расстояния до любого конца сегмента конечности и рассчитанного коэффициента масштабирования для определения длины конечности. По сути, это кажущаяся длина конечности на каждом конце с использованием расстояния до этой точки и коэффициента масштабирования для этого расстояния, как если бы конечность была перпендикулярна наблюдателю. Эти длины считаются вершиной и основанием правильной трапеции с высотой, равной разнице расстояний между двумя точками. Тогда истинную длину конечности можно рассчитать, рассматривая ее как диагональ трапеции.

Расчеты объема

Для расчета объема ствола дерево подразделяется на серию сегментов, причем последовательные диаметры представляют собой нижнюю и верхнюю часть каждого сегмента, а длина сегмента равна разнице в высоте между нижним и верхним диаметрами, или, если ствол не вертикальный. , длину сегмента можно рассчитать по приведенной выше формуле длины конечности. Независимо от того, используете ли вы воздушные или наземные методы, измерения диаметра или обхвата не обязательно должны быть равномерно распределены вдоль ствола дерева, но необходимо провести достаточное количество измерений, чтобы адекватно отобразить изменения диаметра ствола. Совокупный объем ствола рассчитывается путем сложения объемов измеренных сегментов дерева. Если сегменты короткие, объем каждого сегмента рассчитывается как объем усеченного конуса, где объем рассчитывается по любой из трех форм:

${\begin{aligned}{\text{volume}}&={\frac {\pi h(r_{1}^{2}+r_{2}^{2}+r_{1}r_{2})}{3}}\\[4pt]{\text{volume}}&={\frac {\pi h(D_{1}^{2}+D_{2}^{2}+D_{1}D_{2})}{12}}\\[4pt]{\text{volume}}&={\frac {h\left(A_{1}+A_{2}+{\sqrt {A_{1}A_{2}}}\right)}{3}}\end{aligned}}$

где

r ₁ , r ₂ - радиусы верхнего и нижнего круглых сечений,

D ₁ , D ₂ - диаметры верхнего и нижнего круглых сечений,

A ₁ , A ₂ — площади верхнего и нижнего круглых сечений.

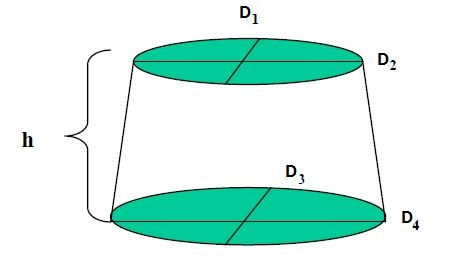
Аналогичную, но более сложную формулу можно использовать, если ствол имеет значительно более эллиптическую форму, где длины большой и малой осей эллипса измеряются вверху и внизу каждого сегмента.

Пусть D ₁ = большая ось верхнего эллипса усеченной пирамиды.

D ₂ = малая ось верхнего эллипса усеченной пирамиды

D ₃ = большая ось нижнего эллипса усеченной пирамиды.

D ₄ = малая ось нижнего эллипса усеченной пирамиды

h = высота усеченного конуса

V = объем детали

π = 3,141593

Затем

${\text{volume}}={\frac {\pi h\left(D_{1}D_{2}+D_{3}D_{4}+{\sqrt {D_{1}D_{2}D_{3}D_{4}}}\right)}{12}}$

Хотя эта формула более сложна, чем эквивалент для круга, если большая и малая оси каждого эллипса равны, результатом будет более знакомая формула для усеченного кругового конуса.

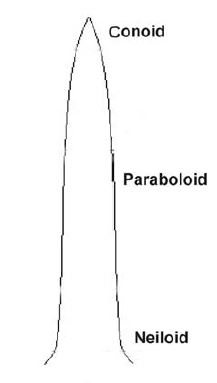
Расчеты объема этих отдельных усеченных сегментов ствола можно уточнить, принимая во внимание общую форму ствола. Стволы деревьев меняют форму или, точнее, несколько раз изгибаются от основания к вершине. Нередко можно увидеть основание дерева нейлоидной формы на расстоянии от 3 до 10 футов. Эта нейлоидная форма затем меняется на цилиндр или параболоид на протяжении примерно нескольких десятков футов, а затем на конус на оставшемся расстоянии.

Форма дерева с высотой

Лучший метод моделирования — разделить ствол на соседние сегменты высотой и длиной не более 3–5 футов, а затем применить к каждому форму конуса, параболоида или усеченного нейлоида. Это трудоемкий процесс. Для повышения эффективности можно выбирать более длинные участки, которые на первый взгляд имеют равномерную кривизну. Однако чем длиннее отрезок, тем важнее выбрать оптимальное твердое тело. На более длинных усеченных конусах становится очевидным больший объемный вклад параболоида или меньший объем нейлоида по сравнению с базовой конической формой. Следовательно, при моделировании более длинных усеченных конусов мерителю необходимо выполнить независимые проверки, чтобы убедиться, что выбрано правильное тело. Один из способов проверки — измерить диаметр в промежуточной точке, а затем спроецировать, каким будет диаметр выбранной модели в этой точке. Если проецируемый диаметр существенно больше или меньше измеренного, то выбранное твердое тело не является правильным выбором. В этом случае может подойти промежуточная форма, объединяющая две формы посредством взвешивания. Измеритель выбирает веса и применяет их к каждой твердой формуле, чтобы получить промежуточный результат. Каждый усеченный конус может представлять собой отдельный родительский конус, параболоид или нейлоид, поэтому нет необходимости придавать единую форму всему дереву.

Формула объема усеченной пирамиды параболоида это: V = ( π h /2)( r ₁ ² + р ₂ ² ), где h = высота усеченного пирамиды, r ₁ — радиус основания усеченного конуса, а r ₂ — радиус вершины усеченного пирамиды. Это позволяет нам использовать усеченный параболоид там, где эта форма кажется более подходящей, чем конус. Затем путем визуального осмотра определяются усеченные конусы.

В качестве расширения этого подхода можно назвать неилоидную форму, стороны которой вогнуты, поэтому ее объем меньше, чем у конуса. Нейлоидная форма часто возникает у основания стволов деревьев с расширяющимися корнями и чуть ниже выпуклостей конечностей. Формула объема усеченной пирамиды нейлоида: V знак равно ( час )[ А _б + ( А _б ² В ) ^1/3 + ( А _б А _и ² ) ^1/3 + A _u ], где A _b — площадь основания, а A _u — площадь вершины усеченного конуса. Этот объем также можно выразить через радиусы:

$V=\left({\frac {h}{4}}\pi \right)\left(r_{b}^{2}+r_{b}^{4/3}r_{u}^{2/3}+r_{b}^{2/3}r_{u}^{4/3}+r_{u}^{2}\right).$

Окончательный объем дерева представляет собой сумму объемов отдельных усеченных участков ствола, объемов секций, измеренных как бифуркации, объема базального выступа, объема разных необычных участков и объемов конечностей (если применимо). .)

Объем меняется со временем

Данные лесного хозяйства показывают, что замедление роста диаметра коррелирует с соразмерным замедлением роста объема, но связь не всегда однозначна. Диаметр представляет собой линейный рост, а объем — это рост в трехмерном контексте. Замедление темпов радиального роста может происходить без замедления роста соответствующей площади поперечного сечения или объема. Леверетт сравнили темпы роста шести молодых белых сосен ( Pinus strobus ) в возрасте от 75 до 90 лет, растущих вдоль Брод-Брук, штат Массачусетс, с темпами роста одиннадцати старых белых сосен из различных других лесных участков вокруг Массачусетса. Как и ожидалось, более мелкие деревья растут с более высокой относительной скоростью, но их фактическое увеличение объема меньше, чем у более крупных деревьев, у которых среднегодовое увеличение объема ствола составляет 6,76 футов. ³ (0,191 м ³ ).

Некоторые из старых сосен государственного леса Могавк-Трейл в западном Массачусетсе растут со скоростью чуть менее чем в два раза быстрее, чем молодые сосны с точки зрения абсолютного увеличения объема, при этом среднегодовое увеличение объема составляет 11,9 кубических футов за указанные периоды времени. Сосна Айс-Глен в Стокбридже , штат Массачусетс, возраст которой, по оценкам, составляет около 300 лет или, возможно, старше, исходя из датировки близлежащих сосен, показывает снижение годового прироста объема примерно до половины от возраста деревьев в возрасте от 90 до 180 лет. класса, но все же в среднем увеличил объем на 5,8 фута. ³ за пятилетний период мониторинга. Это исследование показывает, что эти старые деревья продолжают прибавлять в объеме даже в пожилом возрасте.

Форма туловища с течением времени

Стволы деревьев не только различаются по форме сверху вниз, но и меняются по форме с течением времени. Общую форму ствола дерева можно определить как коэффициент формы: V = F · A · H , где A = площадь основания на заданной высоте (например, 4,5 фута), H = полная высота дерева и F = форм-фактор. Исследования образцов белых сосен в Массачусетсе выявили последовательность прогрессивных изменений формы с течением времени. Было обнаружено, что молодые сосны имеют коэффициент формы от 0,33 до 0,35, сосны, выращенные в лесу в возрасте 150 лет и более, имеют коэффициент формы от 0,36 до 0,44, а коренастые старые сосны-острайники иногда достигают коэффициента формы. от 0,45 до 0,47. Концепция форм-фактора параллельна идее процентного заполнения цилиндра . Объем ствола выражается в процентах от объема цилиндра, имеющего диаметр, равный стволу над прикорневым расширением, и высоту, равную высоте дерева. Цилиндр будет иметь процент заполнения цилиндра 100%, квадратичный параболоид - 50%, конус - 33%, а нейлоид - 25%. Например, старовозрастные деревья болиголова ( Tsuga canadiensis ), измеренные в рамках проекта Tsuga Search Project. Было обнаружено, что процент занятости от 34,8% до 52,3% для отобранных неповрежденных одноствольных деревьев. В целом деревья с толстым основанием или стволом, который быстро сужается, имеют низкие оценки в списке, тогда как деревья, которые сужаются медленнее, имеют более высокие значения. Деревья со сломанными верхушками будут иметь аномально высокие значения. Если диаметр основания взять в пределах области базального блесна, то общий объем будет аномально мал.

Базовые оценки объема

Одна из целей изучения общей формы дерева — найти метод определения общего объема дерева с использованием минимума измерений и обобщенной формулы объема. Самый простой способ добиться этого — смоделировать весь ствол одним применением твердого тела. Применение одной формы ко всему дереву обсуждалось как способ получить быстрое приближение объема. Но этот метод вряд ли даст точный результат.

Учитывая общие изменения формы от основания к вершине дерева и характер изменения фактора формы с течением времени, была разработана прогнозирующая модель , которая была применена к множеству деревьев в Новой Англии , где оценки объема были сделаны на основе измерений высоты дерева. обхват на высоте груди, обхват у корня, а также назначенные значения для коэффициента формы (конусности) и коэффициента расширения. Для молодых и взрослых сосен восточных белых применение площади поперечного сечения при расширении ствола с полной высотой дерева в формуле конуса почти всегда завышает полностью смоделированный объем. Аналогичным образом, использование площади поперечного сечения на высоте груди с полной высотой дерева в формуле конуса обычно занижает объем. Эти значения обеспечивают верхнюю и нижнюю границу фактического объема молодых деревьев. Старовозрастные сосны могут иметь колонновидную форму, и если у них лишь умеренное расширение корней, фактический объем ствола может превышать объем, рассчитанный по формуле верхней границы. При анализе 44 деревьев, включая 42 сосны восточной белой, одно Болиголов восточный и одиночное тюльпановое дерево , среднее значение верхних и нижних объемов по сравнению с смоделированным объемом показывает, что среднее значение, разделенное на смоделированные объемы, составляет 0,98 со стандартным отклонением 0,10. Объемы 34 деревьев попадают в гипотетические верхнюю и нижнюю границы расчета.

Лучшие результаты можно получить, используя субъективно назначенные факторы, учитывающие конусность ствола и характеризующие расширение у основания. Деревья с большим расширением корней или выраженной конусностью искажают формулу. Чрезмерное расширение корней приводит к заметному завышению объема. И наоборот, быстрое сужение ствола приводит к слишком низкому расчетному объему. Эту проблему можно решить, если мы создадим множители для усредненного объема: один для расширения, другой для сужения. Если при визуальном осмотре мы видим большое засветление, мы могли бы использовать множитель засветки 0,90, в противном случае — 1,00. Если бы мы увидели очень медленное снижение, мы могли бы использовать множитель снижения 1,11. Используя отдельные коэффициенты для расширения и конусности и умножая их вместе, чтобы создать составной коэффициент.

$V=F_{1}F_{2}H\left(C_{1}^{2}+{\frac {C_{2}^{2}}{75.4}}\right)$

где C ₁ = окружность корневого расширения, C ₂ = окружность на высоте 4,5 футов, H = полная высота дерева, F ₁ = коэффициент расширения, F ₂ = коэффициент конусности и V = объем. Любое возражение против этого уравнения связано прежде всего с субъективной природой F ₁ и F ₂ . Значение 75,4 = 24 π , где 24 π заменяет коэффициент 12 π в формуле для объема усеченного конуса, охватывающего все дерево, используя одну базальную окружность, преобразуя ее в формулу объема, в которой используется базальная окружность, которая является среднее значение окружностей C ₁ и C _2. Используя отдельные коэффициенты для расширения и конусности и умножая их вместе, мы создаем составной коэффициент. Предполагается, что в некоторых случаях эти расширения и конусы могут быть расширены до значений в диапазоне 0,80 и 1,25, чтобы можно было охарактеризовать крайние формы с помощью формулы. Точно так же модель общего объема туловища потенциально можно предсказать, используя высоту, обхват над базальным расширением и процент заполнения цилиндров для этого вида и возрастного класса. Однако в настоящее время недостаточно данных для проверки этой концепции.

См. также

• правило ветвления да Винчи