Рисование графика

Графическое представление минутной части WWW с указанием гиперссылок .

Рисование графиков — это область математики и информатики, сочетающая методы геометрической теории графов и визуализации информации для получения двумерных изображений графиков , возникающих в результате таких приложений, как анализ социальных сетей , картография , лингвистика и биоинформатика .

Рисунок графа или сетевой диаграммы — это графическое изображение вершин и ребер графа . Этот рисунок не следует путать с самим графиком: одному и тому же графику могут соответствовать самые разные макеты. Говоря абстрактно, важно лишь то, какие пары вершин соединены ребрами. Однако в бетоне расположение этих вершин и ребер на чертеже влияет на его понятность, удобство использования, стоимость изготовления и эстетику . Проблема усугубляется, если граф со временем меняется путем добавления и удаления ребер (динамическое рисование графа), и цель состоит в том, чтобы сохранить мысленную карту пользователя.

Графические соглашения

Ориентированный график со стрелками, показывающими направления ребер.

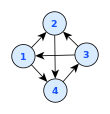
Графы часто рисуются в виде диаграмм узлов и связей, в которых вершины представлены в виде дисков, прямоугольников или текстовых меток, а края представлены в виде отрезков линий , полилиний или кривых на евклидовой плоскости . Диаграммы узлов-связей можно проследить до работ Псевдо-Лулля XIV-XVI веков, которые были опубликованы под именем Рамона Луллия , эрудита XIII века. Псевдо-Лулл ​​рисовал диаграммы такого типа для полных графов , чтобы анализировать все парные комбинации среди наборов метафизических понятий.

В случае ориентированных графов стрелки образуют обычно используемое графическое обозначение для обозначения их ориентации ; однако исследования пользователей показали, что другие соглашения, такие как постепенное сокращение потребления, предоставляют эту информацию более эффективно. При рисовании плоскостей вверх используется соглашение, согласно которому каждое ребро ориентировано от нижней вершины к более высокой вершине, что делает наконечники стрелок ненужными.

Альтернативные соглашения для диаграмм узел-связь включают представления смежности, такие как упаковки кругов , в которых вершины представлены непересекающимися областями на плоскости, а ребра представлены смежностями между областями; представления пересечений , в которых вершины представлены непересекающимися геометрическими объектами, а ребра представлены их пересечениями; представления видимости, в которых вершины представлены областями на плоскости, а края представлены областями, которые имеют беспрепятственную линию обзора друг к другу; сливающиеся рисунки, на которых края представлены плавными кривыми внутри математических железнодорожных путей ; ткани, в которых узлы представлены горизонтальными линиями, а края - вертикальными линиями; и визуализации матрицы смежности графа.

Меры качества

Для графических рисунков было определено множество различных показателей качества в попытке найти объективные средства оценки их эстетики и удобства использования. Помимо управления выбором между различными методами компоновки одного и того же графика, некоторые методы компоновки пытаются напрямую оптимизировать эти показатели.

Плоский граф, нарисованный без перекрывающихся ребер

• Число пересечений рисунка — это количество пар ребер, пересекающих друг друга. Если граф плоский , то часто удобно рисовать его без пересечений ребер; то есть в данном случае рисунок графа представляет собой вложение графа . Однако в приложениях часто возникают непланарные графы, поэтому алгоритмы рисования графов обычно должны учитывать пересечение ребер.
• Площадь рисунка — это размер его наименьшей ограничивающей рамки относительно ближайшего расстояния между любыми двумя вершинами. Рисунки меньшей площади обычно предпочтительнее рисунков большей площади, поскольку они позволяют показать элементы рисунка в большем размере и, следовательно, более разборчиво. Соотношение сторон ограничивающей рамки также может иметь значение.
• Отображение симметрии — это проблема поиска групп симметрии внутри данного графа и поиска рисунка, который отображает как можно большую часть симметрии. Некоторые методы компоновки автоматически приводят к созданию симметричных рисунков; альтернативно, некоторые методы рисования начинаются с поиска симметрий во входном графе и использования их для построения рисунка.
• Важно, чтобы края имели как можно более простую форму, чтобы глазу было легче следить за ними. В полилинейных рисунках сложность ребра может измеряться количеством его изгибов , и многие методы направлены на создание рисунков с небольшим количеством изгибов в целом или с небольшим количеством изгибов на одно ребро. Аналогично для сплайновых кривых сложность ребра может измеряться количеством контрольных точек на ребре.
• Несколько часто используемых показателей качества касаются длины ребер: обычно желательно минимизировать общую длину ребер, а также максимальную длину любого ребра. Кроме того, может оказаться предпочтительным, чтобы длины ребер были одинаковыми, а не сильно различались.
• Угловое разрешение — это мера самых острых углов на графике. Если граф имеет вершины с высокой степенью , то он обязательно будет иметь небольшое угловое разрешение, но угловое разрешение может быть ограничено снизу функцией степени.
• Число наклона графика — это минимальное количество различных наклонов ребер, необходимых для чертежа с ребрами сегментов прямых линий (допускающих пересечения). Кубические графы имеют число наклонов не более четырех, но графы пятой степени могут иметь неограниченное число наклонов; остается открытым вопрос, ограничено ли наклонное число графов степени 4.

Методы компоновки

Силовая сетевая визуализация.

Визуализация компоновки спектрального графика.

Существует множество различных стратегий компоновки графиков:

• В системах компоновки, основанных на силе , программное обеспечение для рисования графов изменяет начальное размещение вершин, непрерывно перемещая вершины в соответствии с системой сил, основанной на физических метафорах, связанных с системами пружин или молекулярной механикой . Обычно эти системы сочетают силы притяжения между соседними вершинами с силами отталкивания между всеми парами вершин, чтобы найти компоновку, в которой длины ребер малы, а вершины хорошо разделены. Эти системы могут выполнять на основе градиентного спуска минимизацию энергетической функции или переводить силы непосредственно в скорости или ускорения движущихся вершин.
• Методы спектральной компоновки используют в качестве координат собственные векторы матрицы , например лапласиан, полученный из матрицы смежности графа.
• Методы ортогональной компоновки, которые позволяют краям графика проходить горизонтально или вертикально параллельно осям координат компоновки. Эти методы изначально были разработаны для задач СБИС и компоновки печатных плат , но они также были адаптированы для рисования графиков. Обычно они включают в себя многоэтапный подход, при котором входной граф планаризуется путем замены точек пересечения вершинами, находится топологическое вложение планаризованного графа, выбираются ориентации ребер для минимизации изгибов, вершины размещаются в соответствии с этими ориентациями и, наконец, создается макет. Стадия уплотнения уменьшает площадь рисунка.
• Алгоритмы компоновки дерева показывают корневое древовидное образование, подходящее для деревьев . Часто в методе, называемом «воздушным шаром», дочерние элементы каждого узла в дереве рисуются на круге, окружающем узел, при этом радиусы этих кругов уменьшаются на более низких уровнях дерева, чтобы эти круги не перекрывались.
• Методы рисования многоуровневых графов (часто называемые рисованием в стиле Сугиямы) лучше всего подходят для ориентированных ациклических графов или графов, которые почти ацикличны, например графиков зависимостей между модулями или функциями в программной системе. В этих методах узлы графа распределяются по горизонтальным слоям с использованием таких методов, как алгоритм Коффмана-Грэма , таким образом, что большинство ребер идут вниз от одного слоя к другому; после этого шага узлы внутри каждого слоя располагаются так, чтобы минимизировать пересечения.

Диаграмма дуги

• Дуговые диаграммы — стиль компоновки, возникший в 1960-х годах. расположить вершины на линии; края могут быть нарисованы в виде полукругов над или под линией или в виде плавных кривых, соединенных вместе из нескольких полукругов.
• Методы круговой компоновки помещают вершины графа в круг, тщательно выбирая порядок вершин вокруг круга, чтобы уменьшить количество пересечений и разместить соседние вершины близко друг к другу. Края могут быть нарисованы либо как хорды круга, либо как дуги внутри или снаружи круга. В некоторых случаях можно использовать несколько кругов.
• При рисовании доминирования вершины размещаются таким образом, что одна вершина расположена вверх, вправо или обе относительно другой тогда и только тогда, когда она достижима из другой вершины. Таким образом, стиль макета делает отношение достижимости графа визуально очевидным.

Графические чертежи для конкретных приложений

Графики и графические рисунки, возникающие в других областях применения, включают:

• Социограммы , рисунки социальной сети , часто предлагаемые программным обеспечением для анализа социальных сетей.
• Диаграммы Хассе — тип графического изображения, предназначенный для частичных порядков.
• Dessin d'enfants — тип графического рисунка, используемый в алгебраической геометрии.
• Диаграммы состояний , графические представления конечных автоматов
• Схемы компьютерных сетей , изображения узлов и соединений в компьютерной сети.
• Блок-схемы и драконовые диаграммы — рисунки, на которых узлы представляют этапы алгоритма , а ребра — поток управления между этапами.
• Диаграммы потоков данных — рисунки, на которых узлы представляют компоненты информационной системы , а края представляют движение информации от одного компонента к другому.
• Биоинформатика , включая филогенетические деревья , сети белок-белковых взаимодействий и метаболические пути .

Кроме того, размещения и маршрутизации этапы электронного проектирования (EDA) во многом аналогичны рисованию графов, как и проблема жадного встраивания в распределенные вычисления , а литература по рисованию графов включает несколько результатов, заимствованных из литературы EDA. Однако эти проблемы также различаются по нескольким важным аспектам: например, в EDA минимизация площади и длина сигнала важнее эстетики, а проблема маршрутизации в EDA может иметь более двух терминалов на сеть, в то время как аналогичная проблема при построении графов вообще включает только пары вершин для каждого ребра.

Программное обеспечение

Интерфейс рисования графиков ( Gephi 0.9.1)

Программное обеспечение, системы и поставщики систем для рисования графиков включают:

• Программное обеспечение с открытым исходным кодом BioFabric для визуализации больших сетей путем рисования узлов в виде горизонтальных линий.
• Cytoscape , программное обеспечение с открытым исходным кодом для визуализации сетей молекулярного взаимодействия.
• Gephi — программное обеспечение для сетевого анализа и визуализации с открытым исходным кодом.
• Graph-tool — бесплатная библиотека Python для анализа графиков.
• Graphviz — система рисования графиков с открытым исходным кодом от корпорации AT&T.
• Linkurious — коммерческое программное обеспечение для сетевого анализа и визуализации графовых баз данных.
• Mathematica — универсальный вычислительный инструмент, включающий в себя инструменты визуализации 2D и 3D графиков и анализа графов.
• Microsoft Automatic Graph Layout , библиотека .NET с открытым исходным кодом (ранее называвшаяся GLEE) для компоновки графиков.
• NetworkX — это библиотека Python для изучения графов и сетей.
• Тюльпан , инструмент визуализации данных с открытым исходным кодом
• yEd , графический редактор с функциональностью макета графика.
• PGF/TikZ 3.0 с graphdrawing пакет (требуется LuaTeX ).
• LaNet-vi , программное обеспечение для визуализации крупных сетей с открытым исходным кодом.

См. также

• Международный симпозиум по рисованию графов
• Список инструментов унифицированного языка моделирования

Ссылки

Общие ссылки

• Ди Баттиста, Джузеппе; Идс, Питер ; Тамассия, Роберто ; Толлис, Иоаннис Г. (1998), Рисование графиков: алгоритмы визуализации графиков , Прентис Холл , ISBN  978-0-13-301615-4 .
• Герман, Иван; Мелансон, Ги; Маршалл, М. Скотт (2000), «Визуализация графов и навигация при визуализации информации: обзор», IEEE Transactions on Visualization and Computer Graphics , 6 (1): 24–43, doi : 10.1109/2945.841119 .
• Младший, Майкл; Мутцель, Петра (2004), программное обеспечение для рисования графиков , Springer-Verlag, ISBN  978-3-540-00881-1 .

Специализированные подтемы

• Андерсон, Джеймс Эндрю; Хед, Томас Дж. (2006), Теория автоматов с современными приложениями , Cambridge University Press, стр. 38–41, ISBN  978-0-521-84887-9 .
• Бахмайер, Кристиан; Брандес, Ульрик ; Шрайбер, Фальк (2014), «Биологические сети», в Тамассии, Роберто (редактор), Справочник по рисованию и визуализации графиков , CRC Press, стр. 621–651 .
• Бастерт, Оливер; Матушевский, Кристиан (2001), «Многослойные рисунки орграфов», Кауфманн, Майкл; Вагнер, Доротея (ред.), Рисование графиков: методы и модели , Конспекты лекций по информатике, том. 2025, Springer-Verlag, стр. 87–120, номер документа : 10.1007/3-540-44969-8_5 , ISBN.  978-3-540-42062-0 .
• Бекман, Брайан (1994), Теория компоновки спектральных графов , Tech. Отчет MSR-TR-94-04, Microsoft Research, заархивирован из оригинала 1 апреля 2016 г. , получен 17 сентября 2011 г.
• Брандес, Ульрик ; Фриман, Линтон К.; Вагнер, Доротея (2014), «Социальные сети», Тамассия, Роберто (редактор), Справочник по рисованию и визуализации графиков , CRC Press, стр. 805–839 .
• Ди Баттиста, Джузеппе; Римондини, Массимо (2014), «Компьютерные сети», Тамассия, Роберто (редактор), Справочник по рисованию и визуализации графиков , CRC Press, стр. 763–803 .
• Догрусёз, Угур; Мэдден, Брендан; Мэдден, Патрик (1997), «Круговая компоновка в наборе инструментов Graph Layout», в Норте, Стивен (редактор), Симпозиум по рисованию графиков, GD '96, Беркли, Калифорния, США, 18–20 сентября 1996 г., Труды , Лекция Заметки по информатике, том. 1190, Springer-Verlag, стр. 92–100, номер документа : 10.1007/3-540-62495-3_40 , ISBN.  978-3-540-62495-0 .
• Эйгльспергер, Маркус; Фекете, Шандор; Клау, Гуннар (2001), «Рисование ортогонального графа», Кауфманн, Майкл; Вагнер, Доротея (ред.), Рисование графиков , Конспекты лекций по информатике, том. 2025, Springer Berlin/Heidelberg, стр. 121–171, doi : 10.1007/3-540-44969-8_6 , ISBN.  978-3-540-42062-0 .
• Фриз, Ральф (2004), «Автоматическое рисование решетки», Эклунд, Питер (редактор), Концептуальные решетки: Вторая международная конференция по формальному концептуальному анализу, ICFCA 2004, Сидней, Австралия, 23–26 февраля 2004 г., Материалы (PDF) ) , Конспекты лекций по информатике, вып. 2961, Springer-Verlag, стр. 589–590, CiteSeerX   10.1.1.69.6245 , doi : 10.1007/978-3-540-24651-0_12 , ISBN  978-3-540-21043-6 , заархивировано (PDF) из оригинала 14 марта 2016 г. , получено 17 сентября 2011 г.
• Гарг, Ашим; Тамассиа, Роберто (1995), «Тестирование восходящей планарности», Order , 12 (2): 109–133, CiteSeerX   10.1.1.10.2237 , doi : 10.1007/BF01108622 , MR   1354797 , S2CID   14183717 .
• Гранжан, Мартен (2014), «Знание — это сеть» , Les Cahiers du Numérique , 10 (3): 37–54, doi : 10.3166/lcn.10.3.37-54 , заархивировано из оригинала 27 июня 2015 г. , получено 15 октября 2014 г.
• Холтен, Дэнни; Айзенберг, Петра ; ван Вейк, Ярке Дж .; Фекете, Жан-Даниэль (2011), «Расширенная оценка читаемости сужающихся, анимированных и текстурированных представлений с направленными краями в графах узловых связей», Тихоокеанский симпозиум по визуализации IEEE (PacificVis 2011) (PDF) , стр. 195– 202, номер домена : 10.1109/PACIFICVIS.2011.5742390 , ISBN  978-1-61284-935-5 , S2CID   16526781 , заархивировано (PDF) из оригинала 11 апреля 2016 г. , получено 29 сентября 2011 г.
• Холтен, Дэнни; ван Вейк, Ярке Дж. (2009), «Исследование пользователей по визуализации направленных ребер в графах», Материалы 27-й Международной конференции по человеческому фактору в вычислительных системах (CHI '09) (PDF) , стр. 2299–2308, CiteSeerX   10.1.1.212.5461 , номер doi : 10.1145/1518701.1519054 , ISBN  9781605582467 , S2CID   9725345 , заархивировано из оригинала (PDF) 6 ноября 2011 г.
• Кнут, Дональд Э. (2013), «Две тысячи лет комбинаторики», Уилсон, Робин; Уоткинс, Джон Дж. (ред.), Комбинаторика: древнее и современное , Oxford University Press, стр. 7–37 .
• Корен, Иегуда (2005), «Построение графиков по собственным векторам: теория и практика», Computers & Mathematics with Applications , 49 (11–12): 1867–1888, doi : 10.1016/j.camwa.2004.08.015 , MR   2154691 .
• Лонгабо, Уильям (2012), «Расчесывание шерсти с помощью BioFabric: новый подход к визуализации больших сетей», BMC Bioinformatics , 13 : 275, doi : 10.1186/1471-2105-13-275 , PMC   3574047 , PMID   23102059 .
• Мэдден, Брендан; Мэдден, Патрик; Пауэрс, Стив; Химсольт, Майкл (1996), «Портативная компоновка и редактирование графиков», в Бранденбурге, Франц Дж. (редактор), Рисование графиков: Симпозиум по рисованию графов, GD '95, Пассау, Германия, 20–22 сентября 1995 г., Труды , Конспекты лекций по информатике, вып. 1027, Springer-Verlag, стр. 385–395, doi : 10.1007/BFb0021822 , ISBN.  978-3-540-60723-6 .
• Мисуэ, К.; Идс, П.; Лай, В.; Сугияма, К. (1995), «Корректировка макета и ментальная карта», Журнал визуальных языков и вычислений , 6 (2): 183–210, doi : 10.1006/jvlc.1995.1010 .
• Нахмансон, Лев; Робертсон, Джордж; Ли, Бонгшин (2008), «Рисование графиков с помощью GLEE», в Хонг, Сок-Хи ; Нисидзеки, Такао ; Цюань, Ву (ред.), Рисование графиков, 15-й Международный симпозиум, GD 2007, Сидней, Австралия, 24–26 сентября 2007 г., Пересмотренные статьи , Конспекты лекций по информатике, том. 4875, Springer-Verlag, стр. 389–394, номер документа : 10.1007/978-3-540-77537-9_38 , ISBN.  978-3-540-77536-2 .
• Пах, Янош ; Шарир, Миха (2009), «5.5 Угловое разрешение и наклоны», Комбинаторная геометрия и ее алгоритмические приложения: Лекции в Алькале , Математические обзоры и монографии, том. 152, Американское математическое общество , стр. 126–127 .
• Покупка, ХК ; Коэн, РФ; Джеймс, Мичиган (1997), «Экспериментальное исследование основ алгоритмов рисования графов», Журнал экспериментальной алгоритмики , 2 , статья 4, doi : 10.1145/264216.264222 , S2CID   22076200 .
• Саати, Томас Л. (1964), «Минимальное число пересечений в полных графах» , Proc. Натл. акад. наук. США , 52 (3): 688–690, Bibcode : 1964PNAS...52..688S , doi : 10.1073/pnas.52.3.688 , PMC   300329 , PMID   16591215 .
• Скотт, Джон (2000), «Социограммы и теория графов», Анализ социальных сетей: справочник (2-е изд.), Sage, стр. 64–69, ISBN  978-0-7619-6339-4 .
• Сугияма, Кодзо ; Тагава, Сёдзиро; Тода, Мицухико (1981), «Методы визуального понимания иерархических системных структур», Транзакции IEEE по системам, человеку и кибернетике , SMC-11 (2): 109–125, doi : 10.1109/TSMC.1981.4308636 , MR   0611436 , S2CID   8367756 .
• Тантау, Тилль (2013), «Рисование графиков в TikZ», Журнал графовых алгоритмов и приложений , 17 (4): 495–513, doi : 10.7155/jgaa.00301 .
• Заппони, Леонардо (август 2003 г.), «Что такое Dessin d'Enfant» (PDF) , Уведомления Американского математического общества , 50 : 788–789, заархивировано (PDF) из оригинала 03 октября 2021 г. , получено в 2021 г. -04-28 .

Дальнейшее чтение

• Ди Баттиста, Джузеппе; Идс, Питер ; Тамассия, Роберто ; Толлис, Иоаннис Г. (1994), «Алгоритмы рисования графов: аннотированная библиография», Вычислительная геометрия: теория и приложения , 4 (5): 235–282, doi : 10.1016/0925-7721(94)00014-x .
• Кауфманн, Майкл; Вагнер, Доротея , ред. (2001), Рисование графиков: методы и модели , Конспекты лекций по информатике , вып. 2025, Springer-Verlag, номер документа : 10.1007/3-540-44969-8 , ISBN.  978-3-540-42062-0 , S2CID   1808286 .
• Тамассия, Роберто , изд. (2014), Справочник по рисованию и визуализации графиков , CRC Press, заархивировано из оригинала 15 августа 2013 г. , получено 28 августа 2013 г.

Внешние ссылки

• Библиотека GraphX ​​для .NET. Архивировано 26 января 2018 г. на Wayback Machine : библиотека WPF с открытым исходным кодом для расчета и визуализации графиков. Поддерживает множество алгоритмов компоновки и маршрутизации ребер.
• Архив электронной печати по рисованию графиков : включая информацию о статьях со всех симпозиумов по рисованию графиков .
• Рисование графиков на сайте Curlie, где можно найти множество дополнительных ссылок, связанных с рисованием графиков.