Акустоэластичный эффект

Акустоупругий эффект — это то, как изменяются скорости звука (как продольные , так и поперечные волны) упругого материала, если он подвергается воздействию поля начальных статических напряжений . Это нелинейный эффект определяющей зависимости между механическим напряжением и конечной деформацией в материале сплошной массы . В классической теории линейной упругости небольшие деформации большинства упругих материалов можно описать линейной зависимостью между приложенным напряжением и результирующей деформацией. Это соотношение широко известно как обобщенный закон Гука . Линейная теория упругости включает упругие постоянные второго порядка (например, $\lambda$ и $\mu$) и обеспечивает постоянную скорость продольного и поперечного звука в упругом материале, на который не влияет приложенное напряжение. С другой стороны, акустоупругий эффект включает расширение определяющего соотношения более высокого порядка (нелинейная теория упругости). ) между приложенным напряжением и результирующей деформацией, что дает скорости продольного и поперечного звука, зависящие от напряженного состояния материала. В пределе ненапряженного материала воспроизводятся скорости звука линейной теории упругости.

Акустоупругий эффект был исследован еще в 1925 году Бриллюэном. Он обнаружил, что скорость распространения акустических волн будет уменьшаться пропорционально приложенному гидростатическому давлению. Однако следствием его теории было то, что звуковые волны перестанут распространяться при достаточно большом давлении. Позже было показано, что этот парадоксальный эффект вызван неверным предположением о том, что давление не влияет на упругие параметры.

В 1937 году Фрэнсис Доминик Мурнаган. представил математическую теорию, расширяющую линейную теорию упругости, включив в нее также конечную деформацию в упругих изотропных материалах. Эта теория включала три упругие константы третьего порядка. $l$, $m$, и $n$. В 1953 году Хьюз и Келли использовали теорию Мурнагана в своей экспериментальной работе для установления численных значений упругих констант более высокого порядка для нескольких упругих материалов, включая полистирол , армко -железо и пирекс , подвергнутых гидростатическому давлению и одноосному сжатию .

Нелинейная теория упругости гиперупругих материалов

Акустоупругий эффект — это эффект конечной деформации нелинейно-упругих материалов. Современный подробный отчет об этом можно найти в . Эта книга посвящена применению нелинейной теории упругости и анализу механических свойств твердых материалов, способных к большим упругим деформациям. Частный случай акустоупругой теории для сжимаемого изотропного гиперупругого материала , такого как поликристаллическая сталь, воспроизведено и показано в этом тексте из нелинейной теории упругости, представленной Огденом.

Обратите внимание , что настройка в этом тексте, а также в является изотермическим не упоминается , и термодинамика .

Определяющее соотношение – гиперупругие материалы (Соотношение напряжения-деформации)

Гиперупругий материал — это частный случай упругого материала Коши , в котором напряжение в любой точке объективно и определяется только текущим состоянием деформации по отношению к произвольной исходной конфигурации (более подробно о деформации см. также страницы Деформация (механика) ) и Конечная деформация ). Однако работа, совершаемая напряжениями, может зависеть от пути деформации. Следовательно, упругий материал Коши имеет неконсервативную структуру, и напряжение не может быть получено из скалярной потенциальной функции упругости . Особый случай упругих материалов Коши, когда работа, совершаемая напряжениями, не зависит от пути деформации, называется упругим по Грину или гиперупругим материалом. Такие материалы консервативны, и напряжения в материале можно определить с помощью скалярного упругого потенциала, более известного как функция плотности энергии деформации .

Определяющая связь между напряжением и деформацией может быть выражена в различных формах в зависимости от выбранных форм напряжения и деформации. Выбор 1-го тензора напряжений Пиолы-Кирхгофа ${\boldsymbol {P}}$ (который представляет собой транспонирование номинального тензора напряжений ${\boldsymbol {P}}^{T}={\boldsymbol {N}}$), материальное уравнение сжимаемого гиперупругого материала можно выразить через лагранжеву деформацию Грина ( ${\boldsymbol {E}}$) как: $${\boldsymbol {P}}={\boldsymbol {F}}\cdot {\frac {\partial W}{\partial {\boldsymbol {E}}}}\qquad {\text{or}}\qquad P_{ij}=F_{ik}~{\frac {\partial W}{\partial E_{kj}}},\qquad i,j=1,2,3~,$$где ${\boldsymbol {F}}$ — тензор градиента деформации , и где второе выражение использует соглашение Эйнштейна о суммировании для индексной записи тензоров . $W$ - это функция плотности энергии деформации для гиперупругого материала , которая определяется на единицу объема, а не на единицу массы, поскольку это позволяет избежать необходимости умножать правую часть на плотность массы. $\rho _{0}$ эталонной конфигурации.

Полагая, что скалярная функция плотности энергии деформации $W({\boldsymbol {E}})$ может быть аппроксимировано разложением в ряд Тейлора по текущей деформации ${\boldsymbol {E}}$, его можно выразить (в индексной записи) как: $$W\approx C_{0}+C_{ij}E_{ij}+{\frac {1}{2!}}C_{ijkl}E_{ij}E_{kl}+{\frac {1}{3!}}C_{ijklmn}E_{ij}E_{kl}E_{mn}+\cdots$$Наложение ограничения на то, что функция энергии деформации должна быть равна нулю и иметь минимум, когда материал находится в недеформированном состоянии (т.е. $W(E_{ij}=0)=0$) ясно, что в функции энергии деформации нет постоянного или линейного члена, и поэтому: $$W\approx {\frac {1}{2!}}C_{ijkl}E_{ij}E_{kl}+{\frac {1}{3!}}C_{ijklmn}E_{ij}E_{kl}E_{mn}+\cdots ,$$где $C_{ijkl}$ – тензор четвертого порядка упругих модулей второго порядка , а $C_{ijklmn}$ — тензор шестого порядка упругих модулей третьего порядка.Симметрия $E_{ij}=E_{ji}$ вместе со скалярной функцией плотности энергии деформации $W$ следует, что модули второго порядка $C_{ijkl}$ имеют следующую симметрию: $$C_{ijkl}=C_{jikl}=C_{ijlk},$$которые уменьшают количество независимых упругих констант с 81 до 36. Кроме того, степенное разложение подразумевает, что модули второго порядка также имеют основную симметрию $$C_{ijkl}=C_{klij},$$что еще больше уменьшает количество независимых упругих постоянных до 21. Те ​​же аргументы можно использовать для упругих модулей третьего порядка $C_{ijklmn}$. Эта симметрия также позволяет выражать упругие модули с помощью обозначений Фойгта (т.е. $C_{ijkl}=C_{IJ}$ и $C_{ijklmn}=C_{IJK}$).

Тензор градиента деформации можно выразить в компонентной форме как $$F_{ij}={\frac {\partial u_{i}}{\partial X_{j}}}+\delta _{ij},$$где $u_{i}$ это смещение материальной точки $P$ от координаты $X_{i}$ в эталонной конфигурации для координации $x_{i}$ в деформированной конфигурации (см. рисунок 2 на странице теории конечных деформаций). Включение степенного разложения функции энергии деформации в определяющее соотношение и замена лагранжева тензора деформации $E_{kl}$ с разложением, данным на странице тензора конечной деформации, дает (обратите внимание, что строчные буквы $u$ использовались в этом разделе по сравнению с верхними буквами на странице конечной деформации ) материальное уравнение $$P_{ij}=C_{ijkl}{\frac {\partial u_{k}}{\partial X_{l}}}+{\frac {1}{2}}M_{ijklmn}{\frac {\partial u_{k}}{\partial X_{l}}}{\frac {\partial u_{m}}{\partial X_{n}}}+{\frac {1}{3}}M_{ijklmnpq}{\frac {\partial u_{k}}{\partial X_{l}}}{\frac {\partial u_{m}}{\partial X_{n}}}{\frac {\partial u_{p}}{\partial X_{q}}}+\cdots ,$$где $$M_{ijklmn}=C_{ijklmn}+C_{ijln}\delta _{km}+C_{jnkl}\delta _{im}+C_{jlmn}\delta _{ik},$$и члены более высокого порядка были проигнорированы (видеть подробные выводы).Для справкиM, пренебрегая членами более высокого порядка в $\partial u_{k}/\partial X_{l}$ это выражение сводится к $P_{ij}=C_{ijkl}{\frac {\partial u_{k}}{\partial X_{l}}},$который является версией обобщенного закона Гука, где $P_{ij}$ является мерой стресса, в то время как $\partial u_{k}/\partial X_{l}$ является мерой напряжения, а $C_{ijkl}$ есть линейная связь между ними.

Скорость звука

Предполагая, что небольшая динамическая (акустическая) деформация нарушает уже статически напряженный материал, акустоупругий эффект можно рассматривать как воздействие на небольшую деформацию, наложенную на большую конечную деформацию (также называемую теорией малого-к-большому). Определим три состояния данной материальной точки. В исходном (ненапряженном) состоянии точка определяется координатным вектором ${\boldsymbol {X}}$ при этом эта же точка имеет координатный вектор ${\boldsymbol {x}}$ в статическом первоначально напряженном состоянии (т.е. под действием приложенного предварительного напряжения). Наконец, предположим, что материальная точка, находящаяся под небольшим динамическим возмущением (полем акустических напряжений), имеет координатный вектор ${\boldsymbol {x'}}$. Тогда общее смещение материальных точек (под влиянием как статического предварительного напряжения, так и динамического акустического возмущения) можно описать векторами смещения $${\boldsymbol {u}}={\boldsymbol {u}}^{(0)}+{\boldsymbol {u}}^{(1)}={\boldsymbol {x'}}-{\boldsymbol {X}},$$где $${\boldsymbol {u}}^{(0)}={\boldsymbol {x}}-{\boldsymbol {X}},\qquad {\boldsymbol {u}}^{(1)}={\boldsymbol {x'}}-{\boldsymbol {x}}$$описывает статическое (лагранжево) начальное смещение из-за приложенного предварительного напряжения и (эйлерово) смещение из-за акустического возмущения соответственно. Первый закон движения Коши (или баланс линейного момента) для дополнительного эйлерова возмущения ${\boldsymbol {u}}^{(1)}$ затем может быть получено через промежуточную лагранжеву деформацию ${\boldsymbol {u}}^{(0)}$ предполагая, что предположение «от малого к большому» $$|{\boldsymbol {u}}^{(1)}|\ll |{\boldsymbol {u}}^{(0)}|$$держит.Использование лагранжевой формы первого закона движения Коши , где пренебрегается действием постоянной массовой силы (т. е. гравитации), дает $$\operatorname {Div} {\boldsymbol {P}}=\rho _{0}{\ddot {{\boldsymbol {x}}'}}.$$

Обратите внимание , что нижний/верхний индекс «0» используется в этом тексте для обозначения ненапряженного эталонного состояния, а переменная с точками, как обычно, представляет собой время ( $t$) производная переменной, и $\operatorname {Div}$ – оператор дивергенции относительно лагранжевой системы координат ${\boldsymbol {X}}$.

Правая часть (зависящая от времени часть) закона движения может быть выражена как $${\begin{aligned}\rho _{0}{\ddot {{\boldsymbol {x}}'}}&=\rho _{0}{\frac {\partial ^{2}}{\partial t^{2}}}({\boldsymbol {u}}^{(0)}+{\boldsymbol {u}}^{(1)}+{\boldsymbol {X}})\\&=\rho _{0}{\frac {\partial ^{2}{\boldsymbol {u}}^{(1)}}{\partial t^{2}}}\end{aligned}}$$в предположении, что как ненапряженное состояние, так и начальное деформированное состояние являются статическими и, следовательно, ${\textstyle \partial ^{2}{\boldsymbol {u}}^{(0)}/\partial t^{2}=\partial ^{2}{\boldsymbol {X}}/\partial t^{2}=0}$.

Для левой части (часть, зависящая от пространства) пространственные частные производные Лагранжа по $X_{j}$ можно разложить по Эйлеру $x_{j}$ используя цепное правило и меняя переменные через соотношение между векторами смещения как $${\frac {\partial }{\partial X_{j}}}={\frac {\partial }{\partial x_{j}}}+u_{k,j}^{(0)}{\frac {\partial }{\partial x_{k}}}+\cdots$$где краткая форма $u_{k,j}^{(0)}\equiv \partial u_{k}^{(0)}/\partial x_{j}$ был использован. Таким образом $${\frac {\partial P_{ij}}{\partial X_{j}}}\approx {\frac {\partial P_{ij}}{\partial x_{j}}}+u_{p.j}^{(0)}{\frac {\partial P_{ij}}{\partial x_{p}}}$$Полагая далее, что статическая начальная деформация ${\boldsymbol {u}}^{(0)}$ (преднапряженное состояние) находится в равновесии, это означает, что $\operatorname {Div} {\boldsymbol {P}}^{(0)}={\boldsymbol {0}}$, и закон движения можно в сочетании с приведенным выше определяющим уравнением свести к линейному соотношению (т.е. когда члены более высокого порядка в $u_{m,n}^{(0)}$) между статической начальной деформацией ${\boldsymbol {u}}^{(0)}$ и дополнительное динамическое возмущение ${\boldsymbol {u}}^{(1)}({\boldsymbol {x}},t)$ как (видеть для подробных выводов) $$B_{ijkl}{\frac {\partial ^{2}u_{k}^{(1)}}{\partial x_{j}\partial x_{l}}}=\rho _{0}{\frac {\partial ^{2}u_{i}^{(1)}}{\partial t^{2}}},$$где $$B_{ijkl}=C_{ijkl}+\delta _{ik}C_{jlqr}u_{q,r}^{(0)}+C_{rjkl}u_{i,r}^{(0)}+C_{irkl}u_{j,r}^{(0)}+C_{ijrl}u_{k,r}^{(0)}+C_{ijkr}u_{l,r}^{(0)}+C_{ijklmn}u_{m,n}^{(0)}.$$Это выражение принято называть линейным волновым уравнением . Рассматривая плоскую волну вида $${\boldsymbol {u}}^{(1)}({\boldsymbol {x}},t)={\boldsymbol {m}}\,f({\boldsymbol {N}}\cdot {\boldsymbol {x}}-ct),$$где ${\boldsymbol {N}}$ — лагранжев единичный вектор в направлении распространения (т. е. параллельно волновому числу ${\boldsymbol {k}}=k{\boldsymbol {N}}$ перпендикулярно фронту волны), ${\boldsymbol {m}}$ — единичный вектор, называемый вектором поляризации (описывающий направление движения частицы), $c$ - скорость фазовой волны, а $f$ — дважды непрерывно дифференцируемая функция (например, синусоидальная функция). Подставляя эту плоскую волну в полученное выше линейное волновое уравнение, получаем $${\boldsymbol {Q}}({\boldsymbol {N}}){\boldsymbol {m}}=\rho _{0}c^{2}{\boldsymbol {m}}$$где ${\boldsymbol {Q}}({\boldsymbol {N}})$ вводится как акустический тензор и зависит от ${\boldsymbol {N}}$ как $$[{\boldsymbol {Q}}({\boldsymbol {N}})]_{ik}=B_{ijkl}N_{j}N_{l}.$$Это выражение называется условием распространения и определяет для данного направления распространения ${\boldsymbol {n}}$ скорость и поляризация возможных волн, соответствующих плоским волнам. Скорости волн можно определить по характеристическому уравнению $$\det({\boldsymbol {Q}}({\boldsymbol {N}})-\rho _{0}c^{2}{\boldsymbol {I}})=0,$$где $\det$ является определяющим и ${\boldsymbol {I}}$ является единичной матрицей .

Для гиперэластичного материала ${\boldsymbol {Q}}({\boldsymbol {N}})$ симметричен (но не вообще), а собственные значения ( $\rho _{0}c^{2}$), таким образом, реальны. Чтобы скорости волн также были действительными, собственные значения должны быть положительными. В этом случае для данного направления распространения существуют три взаимно ортогональные вещественные плоские волны. ${\boldsymbol {N}}$. Из двух выражений акустического тензора ясно, что $$\rho _{0}c^{2}={\boldsymbol {Q}}({\boldsymbol {N}}){\boldsymbol {m}}\cdot {\boldsymbol {m}}=B_{ijkl}N_{j}N_{l}m_{i}m_{k},$$и неравенство $B_{ijkl}N_{j}N_{l}m_{i}m_{k}>0$ (также называемое сильным условием эллиптичности) для всех ненулевых векторов ${\boldsymbol {N}}$ и ${\boldsymbol {m}}$ гарантировать, что скорости однородных плоских волн реальны. Поляризация ${\boldsymbol {m}}={\boldsymbol {N}}$ соответствует продольной волне , в которой движение частицы параллельно направлению распространения (также называемой волной сжатия). Две поляризации, где ${\boldsymbol {m}}\cdot {\boldsymbol {N}}=0$ соответствует поперечным волнам , где движение частиц ортогонально направлению распространения (также называемым поперечными волнами).

Изотропные материалы

Модули упругости для изотропных материалов

Для изотропного тензора второго порядка (т. е. тензора, имеющего одинаковые компоненты в любой системе координат), такого как тензор деформации Лагранжа ${\boldsymbol {E}}$ иметь инварианты $\operatorname {tr} {\boldsymbol {E}}^{q}$ где $\operatorname {tr}$ является оператором трассировки , и $q\in \left\{1,2,3,\dots \right\}$. Таким образом, функция энергии деформации изотропного материала может быть выражена как $W({\boldsymbol {E}})=W(\operatorname {tr} {\boldsymbol {E}}^{q}),\,k\in \left\{1,2,3,\ldots \right\}$или их суперпозицию, которую можно переписать как $$W={\frac {\lambda }{2}}(\operatorname {tr} {\boldsymbol {E}})^{2}+\mu \operatorname {tr} {\boldsymbol {E}}^{2}+{\frac {C}{3}}(\operatorname {tr} {\boldsymbol {E}})^{3}+B(\operatorname {tr} {\boldsymbol {E}})\operatorname {tr} {\boldsymbol {E}}^{2}+{\frac {A}{3}}\operatorname {tr} {\boldsymbol {E}}^{3}+\cdots ,$$где $\lambda ,\mu ,A,B,C$ являются константами. Константы $\lambda$ и $\mu$ – упругие модули второго порядка, более известные как параметры Ламе , а $A,B,$ и $C$ – модули упругости третьего порядка, введенные формулой: которые альтернативны, но эквивалентны $l,m,$ и $n$ представлен Мурнаганом. Объединив это с общим выражением для функции энергии деформации, становится ясно, что $${\begin{aligned}C_{ijkl}&=\lambda \delta _{ij}\delta _{kl}+2\mu \delta I_{ijkl},\\C_{ijklmn}&=2C\delta _{ij}\delta _{kl}\delta _{mn}+2B(\delta _{ij}I_{klmn}+\delta _{kl}I_{mnij}+\delta _{mn}I_{ijkl})+{\frac {1}{2}}A(\delta _{ik}I_{jlmn}+\delta _{il}I_{jkmn}+\delta _{jk}I_{ilmn}+\delta _{jl}I_{ikmn}),\end{aligned}}\!\,$$где $I_{ijkl}={\frac {1}{2}}(\delta _{ik}\delta _{jl}+\delta _{il}\delta _{jk})$. Исторически использовались различные варианты выбора этих упругих констант третьего порядка, некоторые из них показаны в Таблице 1.

Таблица 1: Связь между упругими постоянными третьего порядка для изотропных твердых тел

Ландау и Лифшиц (1986)	Тупен и Бернштейн (1961)	Мурнаган (1951)	Среди (1969)	Эринген и Сухуби (1974)	Стандартный $C_{IJK}$
$A$	$\nu _{1}=2C$	$l=B+C$	$\alpha ={\frac {1}{3}}C$	$l_{E}={\frac {1}{3}}A+B+{\frac {1}{3}}C$	$C_{123}=2C$	$C_{111}=2A+6B+2C$
$B$	$\nu _{2}=B$	$m={\frac {1}{2}}A+B$	$\beta =B$	$m_{E}=-A-2B$	$C_{144}=B$	$C_{112}=2B+2C$
$C$	$\nu _{3}={\frac {1}{4}}A$	$n=A$	$\gamma ={\frac {1}{3}}A$	$n_{E}=A$	$C_{456}={\frac {1}{4}}A$	$C_{166}={\frac {1}{2}}A+B$

Примеры значений для стали

В таблицах 2 и 3 представлены упругие константы второго и третьего порядка для некоторых марок сталей, представленных в литературе.

Таблица 2: Константы Ламе, Тупена и Бернштейна в ГПа

	Постоянные лезвия		Констант Тупен и Бернштейн
Материал	$\lambda$	$\mu$	$\nu _{1}$	$\nu _{2}$	$\nu _{3}$
Гекла 37 (0,4% С)	111 ± 1	82.1 ± 0.5	−385 ± 70	−282 ± 30	−177 ± 8
Гекла 37 (0,6% С)	110.5 ± 1	82.0 ± 0.5	−134 ± 20	−261 ± 20	−167 ± 6
Гекла 138А	109 ± 1	81.9 ± 0.5	−323 ± 50	−265 ± 30	−177 ± 10
Сталь Rex 535 Ni	109 ± 1	81.8 ± 0.5	−175 ± 50	−240 ± 50	−169 ± 15
Hecla ATV аустенитный	87 ± 2	71.6 ± 3	34 ± 20	−552 ± 80	−100 ± 10

Таблица 3: Константы Ламе и Мурнагана в ГПа

	Постоянные лезвия		Константы Мурнагана
Материал	$\lambda$	$\mu$	$l$	$m$	$n$
Никель-сталь С/НВТ	109.0 ± 1	81.7 ± 0.2	−56 ± 20	−671 ± 6	−785 ± 7
Рельсовая сталь образец 1	115.8 ± 2.3%	79.9 ± 2.3%	−248 ± 2.8%	−623 ± 4.1%	−714 ± 2.7%
Рельсовая сталь образец 4	110.7 ± 2.3%	82.4 ± 2.3%	−302 ± 2.8%	−616 ± 4.1%	−724 ± 2.7%

Акустоупругость при одноосном растяжении изотропных гиперупругих материалов

Кубовидный твердого тела в ненапряженной базовой конфигурации может быть образец сжимаемого выражен декартовыми координатами $X_{i}\in [0,L_{i}],\,i=1,2,3$, где геометрия выровнена по лагранжевой системе координат, и $L_{i}$ — длина сторон кубоида в базовой конфигурации. Подвергая кубоид одноосному растяжению в $x_{1}$-направлении так, чтобы он деформировался с чистой однородной деформацией, так что координаты материальных точек в деформированной конфигурации могут быть выражены выражением $x_{1}=\lambda _{1}X_{1},x_{2}=\lambda _{2}X_{2},x_{3}=\lambda _{3}X_{3}$, что даетудлинения $$e_{i}\equiv l_{i}/L_{i}-1=\lambda _{i}-1$$в $x_{i}$-направление. Здесь $l_{i}$ означает текущую (деформированную) длину стороны кубоида $i$ и где отношения длин сторон в текущей и эталонной конфигурации обозначаются через $$\lambda _{i}\equiv l_{i}/L_{i}$$называемые главными участками. Для изотропного материала это соответствует деформации без вращения (см. полярное разложение тензора градиента деформации , где ${\boldsymbol {F}}={\boldsymbol {RU}}={\boldsymbol {VR}}$ и вращение ${\boldsymbol {R}}={\boldsymbol {I}}$). Это можно описать через спектральное представление основных участков. $\lambda _{i}$ как собственные значения или, что то же самое, как удлинения $e_{i}$.

Для одноосного растяжения в $x_{1}$-направление ( $P_{11}>0$ мы предполагаем, что $e_{1}$ увеличиться на некоторую величину. Если боковые грани свободны от тяги (т. е. $P_{22}=P_{33}=0$) боковые удлинения $e_{2}$ и $e_{3}$ ограничены диапазоном $e_{2},e_{3}\in (-1,0]$. Для изотропной симметрии боковые удлинения (или сжатия) также должны быть равны (т.е. $e_{2}=e_{3}$). Диапазон соответствует диапазону от общего латерального сокращения ( $e_{2}=e_{3}=-1$, что является нефизическим) и без изменения поперечных размеров ( $e_{2}=e_{3}=0$). Отмечается, что теоретически диапазон может быть расширен до значений, больших 0, соответствующих увеличению поперечных размеров в результате увеличения осевого размера. Однако очень немногие материалы (так называемые ауксетики ) обладают этим свойством.

Расширение скоростей звука

Плоская продольная (давления) пульсовая волна

Сдвиговая (поперечная) плоская волна

Если выполнено сильное условие эллиптичности ( $B_{ijkl}N_{j}N_{l}m_{i}m_{k}>0$) три ортогональных направления поляризации ( ${\boldsymbol {m}}$ даст ненулевую и реальную скорость звука для данного направления распространения ${\boldsymbol {N}}$. Ниже будут получены скорости звука для одного выбора приложенного одноосного натяжения, направления распространения и ортонормированного набора векторов поляризации. Для одноосного растяжения, приложенного в $x_{1}$-направлении и определение скоростей звука для волн, распространяющихся ортогонально приложенному натяжению (например, в $x_{3}$-направление с вектором распространения ${\boldsymbol {N}}=[0,0,1]$), один выбор ортонормированных поляризаций может быть $$\{{\boldsymbol {m}}\}={\begin{cases}\mathbf {m} _{1}=\mathbf {\hat {x}} _{1}=[1,0,0]&\|\,{\text{to applied tension}}\\\mathbf {m} _{2}=\mathbf {\hat {x}} _{2}=[0,1,0]&\perp {\text{to applied tension}}\\\mathbf {m} _{3}=\mathbf {\hat {x}} _{3}=[0,0,1]&\|\,{\textrm {to}}\,\mathbf {N} \end{cases}}$$что дает три скорости звука $$\rho _{0}c_{33}^{2}=B_{3333},\qquad \rho _{0}c_{31}^{2}=B_{1313},\qquad \rho _{0}c_{32}^{2}=B_{2323},$$где первый индекс $i$ скоростей звука $c_{ij}$ указать направление распространения (здесь $x_{3}$-направление, а второй индекс $j$ указать выбранное направление поляризации ( $j=i$ соответствует движению частицы в направлении распространения $i$ – т.е. продольная волна, и $j\neq i$ соответствует движению частицы перпендикулярно направлению распространения – т.е. сдвиговой волне).

Разложение соответствующих коэффициентов акустического тензора и замена модулей упругости второго и третьего порядка. $C_{ijkl}$ и $C_{ijklmn}$ с их изотропными эквивалентами, $\lambda ,\mu$ и $A,B,C$ соответственно, приводит к скоростям звука, выражаемым как $$\rho _{0}c_{33}^{2}=\lambda +2\mu +a_{33}e_{1},\qquad \rho _{0}c_{3k}^{2}=\mu +a_{3k}e_{1},\quad k=1,2$$где $$a_{33}=-{\frac {2\lambda (\lambda +2\mu )+\lambda A+2(\lambda -\mu )B-2\mu C}{\lambda +\mu }}$$$$a_{31}={\frac {(\lambda +2\mu )(4\mu +A)+4\mu B}{4(\lambda +\mu )}}$$$$a_{32}=-{\frac {\lambda (4\mu +A)-2\mu B}{2(\lambda +\mu )}}$$– коэффициенты акустоупругости, связанные с эффектами упругих постоянных третьего порядка.

Методы измерения

Акустическая установка с преобразователями передатчика и приемника.

Акустическая установка на основе импульсно-эхо

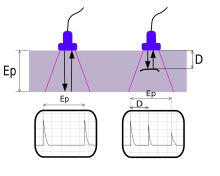
Чтобы иметь возможность измерить скорость звука, а точнее, изменение скорости звука в материале, находящемся в некотором напряженном состоянии, можно измерить скорость акустического сигнала, распространяющегося через рассматриваемый материал. Существует несколько способов сделать это, но все они используют одно из двух физических соотношений скорости звука. Первое соотношение связано со временем, которое требуется сигналу для распространения от одной точки к другой (обычно расстояние между двумя акустическими преобразователями или двукратное расстояние от одного преобразователя до отражающей поверхности). Это часто называют измерениями «времени пролета» (TOF) и используют соотношение $$c={\frac {d}{t}}$$ где $d$ расстояние, которое проходит сигнал, и $t$ это время , необходимое для преодоления этого расстояния. Второе соотношение связано с обратной величиной времени, частоты сигнала. Отношение здесь такое $$c=f\lambda$$ где $f$ частота сигнала и $\lambda$ это длина волны . Измерения с использованием частоты в качестве измеряемой величины используют явление акустического резонанса , где $n$ количество длин волн соответствует длине, на которой сигнал резонирует. Оба эти метода зависят от расстояния, на котором они измеряют, либо напрямую, как во время пролета, либо косвенно через совпадение количества длин волн по физической протяженности резонирующего образца.

Пример методов ультразвукового контроля

В общем, существует два способа настройки системы преобразователей для измерения скорости звука в твердых телах. Один из них представляет собой установку с двумя или более преобразователями, где один действует как передатчик, а другой(и) действует как приемник. Затем измерение скорости звука можно выполнить путем измерения времени между генерацией сигнала в передатчике и моментом его записи в приемнике, предполагая, что известно (или измерено) расстояние, которое акустический сигнал прошел между преобразователями, или наоборот. Измерьте резонансную частоту, зная толщину, на которой резонирует волна. Другой тип установки часто называют системой импульс-эхо . Здесь один преобразователь размещается вблизи образца и действует как передатчик, так и приемник. Для этого требуется отражающий интерфейс, в котором генерируемый сигнал может отражаться обратно к преобразователю, который затем действует как приемник, записывающий отраженный сигнал. См. ультразвуковой контроль некоторых измерительных систем.

Продольные и поляризованные поперечные волны

Диаграмма, показывающая преобразование мод, которое происходит, когда продольная волна падает на границу раздела при ненормальном падении.

Как объяснялось выше, набор из трех ортонормированных поляризаций ( ${\boldsymbol {m}}$) движения частицы существуют для данного направления распространения ${\boldsymbol {N}}$ в твердом виде. Для измерительных установок, в которых преобразователи могут быть закреплены непосредственно на исследуемом образце, можно создать эти три поляризации (одну продольную и две ортогональные поперечные волны), применяя различные типы преобразователей, возбуждающих нужную поляризацию (например, пьезоэлектрические преобразователи с необходимой режим колебаний ). Таким образом, можно измерить скорость звука волн со всеми тремя поляризациями с помощью измерительных установок, зависящих от времени или от частоты, в зависимости от выбора типа преобразователя. Однако если преобразователь невозможно закрепить на испытуемом образце, необходима связующая среда для передачи акустической энергии от преобразователя к образцу. В качестве связующей среды часто используют воду или гели. Для измерения скорости продольного звука этого достаточно, однако жидкости не переносят поперечные волны, и поэтому для того, чтобы иметь возможность генерировать и измерять скорость поперечных волн в испытуемом образце, падающая продольная волна должна взаимодействовать с жидкостью под косым углом. /твердая поверхность для создания поперечных волн через режим преобразования . Такие поперечные волны затем преобразуются обратно в продольные волны на поверхности твердого тела/жидкости, распространяющиеся обратно через жидкость к записывающему преобразователю, позволяющему измерять скорости поперечных волн также через связующую среду.

Приложения

Технические материалы – оценка напряжений

Поскольку отрасль стремится снизить затраты на техническое обслуживание и ремонт, неразрушающий контроль конструкций становится все более ценным как для контроля производства, так и как средство измерения использования и состояния ключевой инфраструктуры. Существует несколько методов измерения напряжения в материале . Однако методы, использующие оптические измерения, магнитные измерения, дифракцию рентгеновских лучей и дифракцию нейтронов , ограничиваются измерением поверхностных или околоповерхностных напряжений или деформаций. Акустические волны легко распространяются через материалы и, таким образом, служат средством исследования внутренней части конструкций, где уровень напряжения и деформации важен для общей структурной целостности .Поскольку скорость звука в таких нелинейно-эластичных материалах (включая распространенные конструкционные материалы, такие как алюминий и сталь ) зависит от напряжения, одним из применений акустоупругого эффекта может быть измерение напряженного состояния внутри нагруженного материала с использованием различных акустических датчиков. (например ультразвуковой контроль ) для измерения изменения скорости звука.

Гранулированные и пористые материалы – геофизика

Сейсмология изучает распространение упругих волн через Землю и используется, например, при изучении землетрясений и при составлении карт недр Земли . Недра Земли подвергаются разному давлению, и поэтому акустические сигналы могут проходить через среды в разных состояниях напряжения. Таким образом, акустоупругая теория может представлять практический интерес, поскольку поведение нелинейных волн можно использовать для оценки геофизических свойств.

Мягкие ткани – медицинский ультразвук

Другими приложениями могут быть медицинская сонография и эластография для измерения уровня напряжения или давления в соответствующих типах эластичных тканей.(например, ), совершенствование неинвазивной диагностики .

См. также

• Акустоэластография
• Конечная деформация
• Скорость звука
• Ультразвуковой контроль