Касательное напряжение

Касательное напряжение
Касательное напряжение
Общие символы	т
единица СИ	паскаль
Выводы из ; другие количества	т = ⁠ F / A ⁠

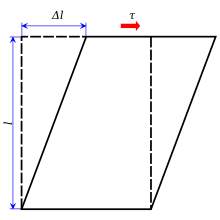
Напряжение сдвига (часто обозначаемое $τ$ , греческое : тау ) является компонентом напряжения , копланарным материала поперечному сечению . Оно возникает из-за поперечной силы , составляющей вектора силы, параллельной поперечному сечению материала. Нормальное напряжение , с другой стороны, возникает из-за составляющей вектора силы, перпендикулярной поперечному сечению материала, на который оно действует.

Общее напряжение сдвига

Формула для расчета среднего напряжения сдвига $τ$ или силы на единицу площади: ^[1] $\tau ={F \over A},$

где:

$F$ , приложенная сила;
$А$ , площадь поперечного сечения.

Задействованная область соответствует грани материала , параллельной вектору приложенной силы, т. е. с вектором нормали к поверхности, перпендикулярным силе.

Другие формы

Напряжение сдвига стены

Напряжение сдвига стенки выражает силу торможения (на единицу площади) со стороны стенки в слоях жидкости, текущей рядом со стеной. Он определяется как: $\tau _{w}:=\mu \left.{\frac {\partial u}{\partial y}}\right|_{y=0}$ где $\mu$ – динамическая вязкость , $u$ скорость потока и $y$ расстояние от стены.

Его используют, например, при описании артериального кровотока , и в этом случае имеются данные о его влиянии на атерогенный процесс. ^[2]

Чистый

Чистое напряжение сдвига связано с чистой деформацией сдвига , обозначаемой $γ$ , следующим уравнением: ^[3] $\tau =\gamma G\,$ где $G$ - модуль сдвига изотропного материала , определяемый формулой $G={\frac {E}{2(1+\nu )}}.$ Здесь $E$ — модуль Юнга , а $ν$ — коэффициент Пуассона .

Сдвиг луча

Сдвиг балки определяется как внутреннее напряжение сдвига балки, вызванное поперечной силой, приложенной к балке. $\tau :={\frac {fQ}{Ib}},$

где

$f$ , общая сила сдвига в рассматриваемом месте;
$Q$ , статический момент площади ;
$b$ — толщина (ширина) материала перпендикулярно сдвигу;
$I$ , момент инерции всей площади поперечного сечения.

Формула сдвига балки также известна как формула напряжения сдвига Журавского в честь Дмитрия Ивановича Журавского, который вывел ее в 1855 году. ^[4]^[5]

Полумонококовые ножницы

Напряжения сдвига в полумонококовой конструкции можно рассчитать путем идеализации поперечного сечения конструкции в виде набора стрингеров (несущих только осевые нагрузки) и перемычек (несущих только сдвиговые потоки ). Разделение сдвигового потока на толщину данной части полумонококовой конструкции дает напряжение сдвига. Таким образом, максимальное касательное напряжение будет возникать либо в ткани максимального сдвигового потока, либо в стенке минимальной толщины.

Конструкции в почве также могут выйти из строя из-за сдвига; например , вес засыпанной землей плотины или дамбы может привести к обрушению недр, подобно небольшому оползню .

Ударный сдвиг

Максимальное напряжение сдвига, создаваемое в твердом круглом стержне, подвергающемся удару, определяется уравнением: $\tau ={\sqrt {\frac {2UG}{V}}},$

где

$U$ , изменение кинетической энергии;
$G$ — модуль сдвига ;
$V$ — объем стержня;

и

$U = U вращающийся + U приложенный$ ;
$U вращающийся = ⁠ 1 / 2 ⁠ Iω 2$ ;
$U применено = Tθ смещено$ ;
$I$ , момент инерции массы;
$ω$ , угловая скорость.

Напряжение сдвига в жидкостях

Любые реальные жидкости ( включая жидкости и газы ), движущиеся вдоль твердой границы, будут испытывать напряжение сдвига на этой границе. Условия отсутствия скольжения ^[6] диктует, что скорость жидкости на границе (относительно границы) равна нулю; хотя на некоторой высоте от границы скорость потока должна быть равна скорости жидкости. Область между этими двумя точками называется пограничным слоем . Для всех ньютоновских жидкостей в ламинарном потоке напряжение сдвига пропорционально скорости деформации жидкости, где вязкость является константой пропорциональности. Для неньютоновских жидкостей не вязкость является постоянной. В результате потери скорости на границу передается напряжение сдвига.

Для ньютоновской жидкости напряжение сдвига на элементе поверхности, параллельном плоской пластине в точке $y,$ определяется выражением: $\tau (y)=\mu {\frac {\partial u}{\partial y}}$

где

$ц$ — динамическая вязкость потока;
$u$ — скорость потока вдоль границы;
$y$ — высота над границей.

В частности, напряжение сдвига стенки определяется как: $\tau _{\mathrm {w} }:=\tau (y=0)=\mu \left.{\frac {\partial u}{\partial y}}\right|_{y=0}~.$

Основополагающий закон Ньютона для любой общей геометрии (включая упомянутую выше плоскую пластину) гласит, что тензор сдвига (тензор второго порядка) пропорционален градиенту скорости потока ( скорость является вектором, поэтому ее градиент является градиентом второго порядка). тензор): ${\boldsymbol {\tau }}(\mathbf {u} )=\mu {\boldsymbol {\nabla }}\mathbf {u}$

а константа пропорциональности называется динамической вязкостью . Для изотропного ньютоновского потока это скаляр, а для анизотропных ньютоновских потоков он может быть и тензором второго порядка. Фундаментальный аспект заключается в том, что для ньютоновской жидкости динамическая вязкость не зависит от скорости потока (т. е. основной закон напряжения сдвига является линейным ), тогда как для неньютоновских течений это неверно, и следует учитывать модификацию: ${\boldsymbol {\tau }}(\mathbf {u} )=\mu (\mathbf {u} ){\boldsymbol {\nabla }}\mathbf {u}$

Это уже не закон Ньютона, а общее тензорное тождество: всегда можно найти выражение вязкости как функции скорости потока, учитывая любое выражение напряжения сдвига как функции скорости потока. С другой стороны, если напряжение сдвига является функцией скорости потока, оно представляет собой ньютоновский поток только в том случае, если его можно выразить как константу для градиента скорости потока. Константа, которую можно найти в этом случае, представляет собой динамическую вязкость потока.

Пример

Учитывая двумерное пространство в декартовых координатах ( x , y ) (компоненты скорости потока соответственно ( u , v )), тогда матрица напряжения сдвига определяется выражением: ${\begin{pmatrix}\tau _{xx}&\tau _{xy}\\\tau _{yx}&\tau _{yy}\end{pmatrix}}={\begin{pmatrix}x{\frac {\partial u}{\partial x}}&0\\0&-t{\frac {\partial v}{\partial y}}\end{pmatrix}}$ представляет собой ньютоновский поток, фактически его можно выразить как: ${\begin{pmatrix}\tau _{xx}&\tau _{xy}\\\tau _{yx}&\tau _{yy}\end{pmatrix}}={\begin{pmatrix}x&0\\0&-t\end{pmatrix}}\cdot {\begin{pmatrix}{\frac {\partial u}{\partial x}}&{\frac {\partial u}{\partial y}}\\{\frac {\partial v}{\partial x}}&{\frac {\partial v}{\partial y}}\end{pmatrix}},$ т. е. анизотропное течение с тензором вязкости: ${\begin{pmatrix}\mu _{xx}&\mu _{xy}\\\mu _{yx}&\mu _{yy}\end{pmatrix}}={\begin{pmatrix}x&0\\0&-t\end{pmatrix}}$ которая является неоднородной (зависит от пространственных координат) и нестационарной, но, соответственно, не зависит от скорости потока: ${\boldsymbol {\mu }}(x,t)={\begin{pmatrix}x&0\\0&-t\end{pmatrix}}$

Следовательно, этот поток является ньютоновским. С другой стороны, поток, в котором вязкость составляла: ${\begin{pmatrix}\mu _{xx}&\mu _{xy}\\\mu _{yx}&\mu _{yy}\end{pmatrix}}={\begin{pmatrix}{\frac {1}{u}}&0\\0&{\frac {1}{u}}\end{pmatrix}}$ является неньютоновским, поскольку вязкость зависит от скорости потока. Этот неньютоновский поток изотропен (матрица пропорциональна единичной матрице), поэтому вязкость является просто скаляром: $\mu (u)={\frac {1}{u}}$

Измерение с помощью датчиков

Датчик напряжения сдвига с расходящейся кромкой

Эту зависимость можно использовать для измерения напряжения сдвига стенки. Если бы датчик мог напрямую измерять градиент профиля скорости у стенки, то умножение на динамическую вязкость дало бы напряжение сдвига. Такой датчик продемонстрировали А. А. Накви и У. К. Рейнольдс. ^[7] Интерференционная картина, возникающая при прохождении луча света через две параллельные щели, образует сеть линейно расходящихся полос, которые, кажется, исходят из плоскости двух щелей (см. эксперимент с двумя щелями ). Когда частица в жидкости проходит через полосы, приемник обнаруживает отражение рисунка полос. Сигнал можно обработать и, зная угол интерференции, экстраполировать высоту и скорость частицы. Измеренное значение градиента скорости стенки не зависит от свойств жидкости и, как следствие, не требует калибровки. Последние достижения в технологиях изготовления микрооптики позволили использовать интегрированный дифракционный оптический элемент для изготовления датчиков напряжения сдвига с расходящимися полосами, которые можно использовать как в воздухе, так и в жидкости. ^[8]

Микростолбовой датчик напряжения сдвига

Еще одним методом измерения является использование тонких настенных микроколонн, изготовленных из гибкого полимера ПДМС, которые изгибаются в ответ на действие сил сопротивления вблизи стены. Таким образом, датчик относится к принципу косвенного измерения, основанному на взаимосвязи между пристеночными градиентами скорости и локальным напряжением сдвига у стенки. ^[9]^[10]

Электродиффузионный метод

Электродиффузионным методом измеряют скорость сдвига стенки в жидкой фазе микроэлектрода в условиях предельного диффузионного тока. Разность потенциалов между анодом с широкой поверхностью (обычно расположенным далеко от зоны измерения) и небольшим рабочим электродом, выполняющим роль катода, приводит к быстрой окислительно-восстановительной реакции. Исчезновение ионов происходит только на активной поверхности микрозонда, вызывая развитие диффузионного пограничного слоя, в котором скорость быстрой электродиффузионной реакции контролируется только диффузией. Разрешение уравнения конвективно-диффузии в пристеночной области микроэлектрода приводит к аналитическим решениям, основанным на характеристиках длины микрозондов, диффузионных свойствах электрохимического раствора и скорости сдвига стенки. ^[11]

См. также

Ссылки

^ Хиббелер, Р.К. (2004). Механика материалов . Нью-Джерси, США: Pearson Education. п. 32. ISBN 0-13-191345-Х .
^ Катрицис, Демосфен (2007). «Напряжение сдвига в стене: теоретические соображения и методы измерения». Прогресс в сердечно-сосудистых заболеваниях . 49 (5): 307–329. дои : 10.1016/j.pcad.2006.11.001 . ПМИД 17329179 .
^ «Сопротивление материалов» . Eformulae.com . Проверено 24 декабря 2011 г.
^ Лекция Формула Журавского [Zhuravskii's Formula]. Сопромат Лекции (in Russian) . Retrieved 2014-02-26 .
^ «Изгиб балок» (PDF) . Лекции по машиностроению . Университет Макмастера . ^{[ постоянная мертвая ссылка ]}
^ Дэй, Майкл А. (2004), «Условие прилипания гидродинамики» , Erkenntnis , 33 (3), Springer Нидерланды: 285–296, doi : 10.1007/BF00717588 , ISSN 0165-0106 , S2CID 55186899 .
^ Накви, А.А.; Рейнольдс, У.К. (январь 1987 г.), «Двойной цилиндрический волновой лазерно-доплеровский метод для измерения поверхностного трения в потоке жидкости», Технический отчет NASA STI/Recon N , 87
^ {Датчик напряжения сдвига microS, MSE}
^ Гроссе, С.; Шредер, В. (2009), «Двумерная визуализация турбулентного напряжения сдвига стенки с использованием микростолбов», AIAA Journal , 47 (2): 314–321, Бибкод : 2009AIAAJ..47..314G , doi : 10.2514/1.36892
^ Гроссе, С.; Шредер, В. (2008), «Измерение динамического напряжения сдвига стенки в турбулентном потоке в трубе с использованием микростолбчатого датчика MPS». ³", Международный журнал по теплу и потоку жидкости , 29 (3): 830–840, doi : 10.1016/j.ijheatfluidflow.2008.01.008.
^ Хавлица, Дж.; Крамолис, Д.; Хучет, Ф. (2021), «Возврат к электродиффузионной теории для измерения напряжения сдвига в стенках» (PDF) , International Journal of Heat and Mass Transfer , 165 : 120610, doi : 10.1016/j.ijheatmasstransfer.2020.120610 , S2CID 228876357

[1] Хиббелер, Р.К. (2004). Механика материалов . Нью-Джерси, США: Pearson Education. п. 32. ISBN 0-13-191345-Х .

[2] Катрицис, Демосфен (2007). «Напряжение сдвига в стене: теоретические соображения и методы измерения». Прогресс в сердечно-сосудистых заболеваниях . 49 (5): 307–329. дои : 10.1016/j.pcad.2006.11.001 . ПМИД 17329179 .

[3] «Сопротивление материалов» . Eformulae.com . Проверено 24 декабря 2011 г.

[4] Лекция Формула Журавского [Zhuravskii's Formula]. Сопромат Лекции (in Russian) . Retrieved 2014-02-26 .

[5] «Изгиб балок» (PDF) . Лекции по машиностроению . Университет Макмастера . ^{[ постоянная мертвая ссылка ]}

[6] Дэй, Майкл А. (2004), «Условие прилипания гидродинамики» , Erkenntnis , 33 (3), Springer Нидерланды: 285–296, doi : 10.1007/BF00717588 , ISSN 0165-0106 , S2CID 55186899 .

[7] Накви, А.А.; Рейнольдс, У.К. (январь 1987 г.), «Двойной цилиндрический волновой лазерно-доплеровский метод для измерения поверхностного трения в потоке жидкости», Технический отчет NASA STI/Recon N , 87

[8] {Датчик напряжения сдвига microS, MSE}

[9] Гроссе, С.; Шредер, В. (2009), «Двумерная визуализация турбулентного напряжения сдвига стенки с использованием микростолбов», AIAA Journal , 47 (2): 314–321, Бибкод : 2009AIAAJ..47..314G , doi : 10.2514/1.36892

[10] Гроссе, С.; Шредер, В. (2008), «Измерение динамического напряжения сдвига стенки в турбулентном потоке в трубе с использованием микростолбчатого датчика MPS». ³", Международный журнал по теплу и потоку жидкости , 29 (3): 830–840, doi : 10.1016/j.ijheatfluidflow.2008.01.008.

[11] Хавлица, Дж.; Крамолис, Д.; Хучет, Ф. (2021), «Возврат к электродиффузионной теории для измерения напряжения сдвига в стенках» (PDF) , International Journal of Heat and Mass Transfer , 165 : 120610, doi : 10.1016/j.ijheatmasstransfer.2020.120610 , S2CID 228876357

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

Касательное напряжение
Общие символы	$т$
единица СИ	паскаль
Выводы из другие количества	$т = .mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion,.mw-parser-output .sfrac .tion{display:inline-block;vertical-align:-0.5em;font-size:85%;text-align:center}.mw-parser-output .sfrac .num{display:block;line-height:1em;margin:0.0em 0.1em;border-bottom:1px solid}.mw-parser-output .sfrac .den{display:block;line-height:1em;margin:0.1em 0.1em}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);clip-path:polygon(0px 0px,0px 0px,0px 0px);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px}⁠ F / A ⁠$