Уравнение Хагена – Пуазейля

В динамике неидеальных жидкостей уравнение Хагена -Пуазейля , также известное как закон Хагена-Пуазейля , закон Пуазейля или уравнение Пуазейля , представляет собой физический закон , который определяет падение давления в несжимаемой и ньютоновской жидкости в ламинарном потоке, текущем через длинную цилиндрическую трубу. постоянного сечения. Его можно с успехом применять для контроля потока воздуха в легких альвеолах , а также для потока через трубочку для питья или через иглу для подкожных инъекций . Он был независимо экспериментально выведен Жаном Леонаром Мари Пуазейлем в 1838 году. ^[1] и Готхильф Генрих Людвиг Хаген , ^[2] и опубликовано Хагеном в 1839 году. ^[1] а затем Пуазейлем в 1840–41 и 1846 годах. ^[1] Теоретическое обоснование закона Пуазейля дал Джордж Стоукс в 1845 году. ^[3]

Допущения уравнения заключаются в том, что жидкость несжимаема и ньютонова ; течение ламинарное в трубе постоянного круглого сечения, существенно превышающей ее диаметр; нет и ускорения жидкости в трубе . При скоростях и диаметрах труб, превышающих пороговое значение, фактический поток жидкости является не ламинарным, а турбулентным , что приводит к большему перепаду давления, чем рассчитано по уравнению Хагена – Пуазейля.

Уравнение Пуазейля описывает падение давления из-за вязкости жидкости; в жидкости все еще могут возникать другие типы перепадов давления (см. демонстрацию здесь). ^[4] Например, давление, необходимое для того, чтобы поднять вязкую жидкость против силы тяжести, будет содержать как то, что необходимо в законе Пуазейля, так и то, что необходимо в уравнении Бернулли , так что в любой точке потока давление будет больше нуля (в противном случае поток не будет случаться).

Другой пример: когда кровь течет в более узкое сужение , ее скорость будет больше, чем в большем диаметре (из-за непрерывности объемной скорости потока ), а ее давление будет ниже, чем в большем диаметре. ^[4] (из-за уравнения Бернулли). Однако вязкость крови вызовет дополнительное падение давления в направлении потока, пропорциональное пройденной длине. ^[4] (по закону Пуазейля). Оба эффекта способствуют фактическому падению давления.

Уравнение

В стандартных обозначениях кинетики жидкости: ^[5]^[6]^[7]

\Delta p={\frac {8\mu LQ}{\pi R^{4}}}={\frac {8\pi \mu LQ}{A^{2}}},

где

Δp —

разница давлений между двумя концами,

L

– длина трубы,

μ

— динамическая вязкость ,

Q

– объемный расход ,

R

– радиус трубы,

А

– площадь поперечного сечения трубы.

Уравнение не выполняется вблизи входа в трубу. ^[8]^: 3

Уравнение не работает в пределе низкой вязкости, широкой и/или короткой трубы. Низкая вязкость или широкая труба могут привести к турбулентному потоку, что приводит к необходимости использования более сложных моделей, таких как уравнение Дарси-Вейсбаха . отношение длины к радиусу трубы должно быть больше 1/48 числа Рейнольдса . Чтобы закон Хагена-Пуазейля был действительным, ^[9] Если труба слишком короткая, уравнение Хагена – Пуазейля может привести к нефизически высоким скоростям потока; поток ограничен принципом Бернулли , при менее ограничительных условиях,

{\begin{aligned}\Delta p={\frac {1}{2}}\rho {\overline {v}}_{\text{max}}^{2}&={\frac {1}{2}}\rho \left({\frac {Q_{\text{max}}}{\pi R^{2}}}\right)^{2}\\\Rightarrow \quad Q_{\max }{}&=\pi R^{2}{\sqrt {\frac {2\Delta p}{\rho }}},\end{aligned}}

потому что невозможно иметь отрицательное (абсолютное) давление (не путать с манометрическим давлением ) в несжимаемом потоке.

Связь с уравнением Дарси – Вейсбаха

Обычно течение Хагена – Пуазейля подразумевает не только приведенное выше соотношение для перепада давления, но и полное решение для профиля ламинарного потока, который является параболическим. Однако результат для падения давления можно распространить на турбулентный поток, сделав вывод об эффективной турбулентной вязкости в случае турбулентного потока, даже несмотря на то, что профиль потока в турбулентном потоке, строго говоря, не является параболическим. В обоих случаях, ламинарном или турбулентном, падение давления связано с напряжением на стенке, которое определяет так называемый коэффициент трения. Напряжение стенки может быть определено феноменологически с помощью уравнения Дарси-Вейсбаха в области гидравлики , учитывая соотношение коэффициента трения через число Рейнольдса. В случае ламинарного течения для круглого сечения:

\Lambda ={\frac {64}{\mathrm {Re} }},\quad \mathrm {Re} ={\frac {\rho vd}{\mu }},

где $Re$ — число Рейнольдса , $ρ$ — плотность жидкости, а $v$ — средняя скорость потока, которая составляет половину максимальной скорости потока в случае ламинарного потока. Гораздо полезнее определять число Рейнольдса через среднюю скорость потока, поскольку эта величина остается четко определенной даже в случае турбулентного потока, тогда как максимальная скорость потока может и не быть таковой или, в любом случае, ее может быть трудно определить. . В этой форме закон аппроксимирует коэффициент трения Дарси , коэффициент потерь энергии (напора) , коэффициент потерь на трение или коэффициент Дарси (трения) $Λ$ в ламинарном потоке при очень низких скоростях в цилиндрической трубе. Теоретический вывод несколько иной формы закона был сделан независимо Видманом в 1856 г. и Нейманом и Э. Хагенбахом в 1858 г. (1859, 1860). Хагенбах был первым, кто назвал этот закон законом Пуазейля.

Закон также очень важен в гемореологии и гемодинамике , обеих областях физиологии . ^[10]

Позже, в 1891 году, закон Пуазейля был распространен на турбулентный поток Л. Р. Уилберфорсом на основе работы Хагенбаха.

Вывод

Уравнение Хагена-Пуазейля может быть получено из уравнений Навье-Стокса . Ламинарное течение в трубе однородного (круглого) сечения известно как течение Хагена – Пуазейля. Уравнения, управляющие потоком Хагена – Пуазейля, могут быть получены непосредственно из уравнений импульса Навье – Стокса в трехмерных цилиндрических координатах $(r, θ, x),$ сделав следующий набор предположений:

Течение стабильное( $.mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion,.mw-parser-output .sfrac .tion{display:inline-block;vertical-align:-0.5em;font-size:85%;text-align:center}.mw-parser-output .sfrac .num{display:block;line-height:1em;margin:0.0em 0.1em;border-bottom:1px solid}.mw-parser-output .sfrac .den{display:block;line-height:1em;margin:0.1em 0.1em}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);clip-path:polygon(0px 0px,0px 0px,0px 0px);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px}⁠ ∂... / ∂ t ⁠ = 0$ ).
Радиальная и азимутальная составляющие скорости жидкости равны нулю ( $u r = u θ = 0$ ).
Течение осесимметричное ( $⁠ \partial... / \partial θ ⁠ = 0$ ).
Поток полностью развит( $⁠ \partial ты Икс / \partial Икс ⁠ знак равно 0$ ). Однако здесь это можно доказать с помощью сохранения массы и приведенных выше предположений.

Тогда угловое уравнение в уравнениях количества движения и уравнение неразрывности удовлетворяются тождественно. Уравнение радиального момента сводится к $⁠ \partial p / \partial r ⁠ = 0$ , т. е. давление $p$ является функцией только осевой координаты $x$ . Для краткости используйте $u$ вместо $u_{x}$ . Уравнение осевого момента сводится к

{\frac {1}{r}}{\frac {\partial }{\partial r}}\left(r{\frac {\partial u}{\partial r}}\right)={\frac {1}{\mu }}{\frac {\mathrm {d} p}{\mathrm {d} x}}

где $ц$ — динамическая вязкость жидкости. В приведенном выше уравнении левая часть является только функцией $r$ , а член правой части — только функцией $x$ , подразумевая, что оба члена должны быть одной и той же константой. Оценить эту константу несложно. Если мы возьмем длину трубы равной $L$ и обозначим разницу давлений между двумя концами трубы через $Δ p$ (высокое давление минус низкое давление), то константа будет просто

-{\frac {\mathrm {d} p}{\mathrm {d} x}}={\frac {\Delta p}{L}}=G

определено так, что $G$ положительна. Решение

u=-{\frac {Gr^{2}}{4\mu }}+c_{1}\ln r+c_{2}

Поскольку $u$ должно быть конечным в точке $r = 0$ , $c 1 = 0$ . прилипания Граничное условие на стенке трубы требует, чтобы $u = 0$ при $r = R$ (радиус трубы), что дает $c 2 = ⁠ GR 2 / 4 мкм ⁠$ . Таким образом, мы наконец имеем следующий параболический профиль скорости :

u={\frac {G}{4\mu }}\left(R^{2}-r^{2}\right).

Максимальная скорость возникает на центральной линии трубы ( $r = 0$ ), $u max = ⁠ GR 2 / 4 мкм ⁠$ . Среднюю скорость можно получить путем интегрирования по поперечному сечению трубы :

{u}_{\mathrm {avg} }={\frac {1}{\pi R^{2}}}\int _{0}^{R}2\pi ru\mathrm {d} r={\tfrac {1}{2}}{u}_{\mathrm {max} }.

Легко измеримой величиной в экспериментах является объемный расход $Q = π R 2 ты в среднем$ . Перестановка этого дает уравнение Хагена – Пуазейля

\Delta p={\frac {8\mu QL}{\pi R^{4}}}.

Тщательно продуманный вывод, начинающийся непосредственно с первых принципов.

Although more lengthy than directly using the Navier–Stokes equations, an alternative method of deriving the Hagen–Poiseuille equation is as follows.

Liquid flow through a pipe

Assume the liquid exhibits laminar flow. Laminar flow in a round pipe prescribes that there are a bunch of circular layers (lamina) of liquid, each having a velocity determined only by their radial distance from the center of the tube. Also assume the center is moving fastest while the liquid touching the walls of the tube is stationary (due to the no-slip condition).

To figure out the motion of the liquid, all forces acting on each lamina must be known:

The pressure force pushing the liquid through the tube is the change in pressure multiplied by the area: $F = - A Δ p$ . This force is in the direction of the motion of the liquid. The negative sign comes from the conventional way we define $Δ p = p end - p top < 0$ .
Viscosity effects will pull from the faster lamina immediately closer to the center of the tube.
Viscosity effects will drag from the slower lamina immediately closer to the walls of the tube.

Viscosity

Two fluids moving past each other in the $x$ direction. The liquid on top is moving faster and will be pulled in the negative direction by the bottom liquid while the bottom liquid will be pulled in the positive direction by the top liquid.

When two layers of liquid in contact with each other move at different speeds, there will be a shear force between them. This force is proportional to the area of contact $A$ , the velocity gradient perpendicular to the direction of flow $⁠ Δ v x / Δ y ⁠$ , and a proportionality constant (viscosity) and is given by

F_{\text{viscosity, top}}=-\mu A{\frac {\Delta v_{x}}{\Delta y}}.

The negative sign is in there because we are concerned with the faster moving liquid (top in figure), which is being slowed by the slower liquid (bottom in figure). By Newton's third law of motion, the force on the slower liquid is equal and opposite (no negative sign) to the force on the faster liquid. This equation assumes that the area of contact is so large that we can ignore any effects from the edges and that the fluids behave as Newtonian fluids.

Faster lamina

Assume that we are figuring out the force on the lamina with radius $r$ . From the equation above, we need to know the area of contact and the velocity gradient. Think of the lamina as a ring of radius $r$ , thickness $dr$ , and length $Δ x$ . The area of contact between the lamina and the faster one is simply the surface area of the cylinder: $A = 2π r Δ x$ . We don't know the exact form for the velocity of the liquid within the tube yet, but we do know (from our assumption above) that it is dependent on the radius. Therefore, the velocity gradient is the change of the velocity with respect to the change in the radius at the intersection of these two laminae. That intersection is at a radius of $r$ . So, considering that this force will be positive with respect to the movement of the liquid (but the derivative of the velocity is negative), the final form of the equation becomes

F_{\text{viscosity, fast}}=-2\pi r\mu \,\Delta x\,\left.{\frac {\mathrm {d} v}{\mathrm {d} r}}\right|_{r}

where the vertical bar and subscript $r$ following the derivative indicates that it should be taken at a radius of $r$ .

Slower lamina

Next let's find the force of drag from the slower lamina. We need to calculate the same values that we did for the force from the faster lamina. In this case, the area of contact is at $r + d r$ instead of $r$ . Also, we need to remember that this force opposes the direction of movement of the liquid and will therefore be negative (and that the derivative of the velocity is negative).

F_{\text{viscosity, slow}}=2\pi (r+\mathrm {d} r)\mu \,\Delta x\left.{\frac {\mathrm {d} v}{\mathrm {d} r}}\right|_{r+\mathrm {d} r}

Putting it all together

To find the solution for the flow of a laminar layer through a tube, we need to make one last assumption. There is no acceleration of liquid in the pipe, and by Newton's first law, there is no net force. If there is no net force then we can add all of the forces together to get zero

0=F_{\text{pressure}}+F_{\text{viscosity, fast}}+F_{\text{viscosity, slow}}

or

0=-\Delta p2\pi r\,\mathrm {d} r-2\pi r\mu \,\Delta x\left.{\frac {\mathrm {d} v}{\mathrm {d} r}}\right|_{r}+2\pi (r+\mathrm {d} r)\mu \,\Delta x\,\left.{\frac {\mathrm {d} v}{\mathrm {d} r}}\right\vert _{r+\mathrm {d} r}.

First, to get everything happening at the same point, use the first two terms of a Taylor series expansion of the velocity gradient:

\left.{\frac {\mathrm {d} v}{\mathrm {d} r}}\right|_{r+\mathrm {d} r}=\left.{\frac {\mathrm {d} v}{\mathrm {d} r}}\right|_{r}+\left.{\frac {\mathrm {d} ^{2}v}{\mathrm {d} r^{2}}}\right|_{r}\,\mathrm {d} r.

The expression is valid for all laminae. Grouping like terms and dropping the vertical bar since all derivatives are assumed to be at radius $r$ ,

0=-\Delta p2\pi r\,\mathrm {d} r+2\pi \mu \,\mathrm {d} r\,\Delta x{\frac {\mathrm {d} v}{\mathrm {d} r}}+2\pi r\mu \,\mathrm {d} r\,\Delta x{\frac {\mathrm {d} ^{2}v}{\mathrm {d} r^{2}}}+2\pi \mu (\mathrm {d} r)^{2}\,\Delta x{\frac {\mathrm {d} ^{2}v}{\mathrm {d} r^{2}}}.

Finally, put this expression in the form of a differential equation, dropping the term quadratic in $dr$ .

{\frac {1}{\mu }}{\frac {\Delta p}{\Delta x}}={\frac {\mathrm {d} ^{2}v}{\mathrm {d} r^{2}}}+{\frac {1}{r}}{\frac {\mathrm {d} v}{\mathrm {d} r}}

The above equation is the same as the one obtained from the Navier–Stokes equations and the derivation from here on follows as before.

Запуск потока Пуазейля в трубе

При постоянном градиенте давления $G = - ⁠ d p / d x ⁠$ применяется между двумя концами длинной трубы, поток не сразу приобретает профиль Пуазейля, а развивается со временем и достигает профиля Пуазейля в установившемся состоянии. Уравнения Навье – Стокса сводятся к

{\frac {\partial u}{\partial t}}={\frac {G}{\rho }}+\nu \left({\frac {\partial ^{2}u}{\partial r^{2}}}+{\frac {1}{r}}{\frac {\partial u}{\partial r}}\right)

с начальными и граничными условиями,

u(r,0)=0,\quad u(R,t)=0.

Распределение скорости определяется выражением

u(r,t)={\frac {G}{4\mu }}\left(R^{2}-r^{2}\right)-{\frac {2GR^{2}}{\mu }}\sum _{n=1}^{\infty }{\frac {1}{\lambda _{n}^{3}}}{\frac {J_{0}(\lambda _{n}r/R)}{J_{1}(\lambda _{n})}}e^{-\lambda _{n}^{2}\nu t/R^{2}},\quad J_{0}\left(\lambda _{n}\right)=0

где $J 0 (⁠ λ n r / R ⁠)$ — функция Бесселя первого рода нулевого порядка, $λ n$ — положительные корни этой функции, а $J 1 (λ n)$ — функция Бесселя первого рода первого порядка. При $t \to \infty$ решение Пуазейля восстанавливается. ^[11]

Течение Пуазейля в кольцевом сечении

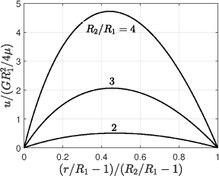
Если $R 1$ — радиусы внутреннего цилиндра, а $R 2$ — радиусы внешнего цилиндра, с постоянным градиентом приложенного давления между двумя концами $G = — ⁠ d p / d x ⁠$ , распределение скорости и объемный поток через кольцевую трубу равны

{\begin{aligned}u(r)&={\frac {G}{4\mu }}\left(R_{1}^{2}-r^{2}\right)+{\frac {G}{4\mu }}\left(R_{2}^{2}-R_{1}^{2}\right){\frac {\ln r/R_{1}}{\ln R_{2}/R_{1}}},\\[6pt]Q&={\frac {G\pi }{8\mu }}\left[R_{2}^{4}-R_{1}^{4}-{\frac {\left(R_{2}^{2}-R_{1}^{2}\right)^{2}}{\ln R_{2}/R_{1}}}\right].\end{aligned}}

Когда $R 2 = R$ , $R 1 = 0$ , исходная проблема восстанавливается. ^[12]

Течение Пуазейля в трубе с осциллирующим градиентом давления

Поток через трубы с колеблющимся градиентом давления находит применение в кровотоке через крупные артерии. ^[13]^[14]^[15]^[16] Наложенный градиент давления определяется выражением

{\frac {\partial p}{\partial x}}=-G-\alpha \cos \omega t-\beta \sin \omega t

где $G$ , $α$ и $β$ — константы, а $ω$ — частота. Поле скорости определяется выражением

u(r,t)={\frac {G}{4\mu }}\left(R^{2}-r^{2}\right)+[\alpha F_{2}+\beta (F_{1}-1)]{\frac {\cos \omega t}{\rho \omega }}+[\beta F_{2}-\alpha (F_{1}-1)]{\frac {\sin \omega t}{\rho \omega }}

где

{\begin{aligned}F_{1}(kr)&={\frac {\mathrm {ber} (kr)\mathrm {ber} (kR)+\mathrm {bei} (kr)\mathrm {bei} (kR)}{\mathrm {ber} ^{2}(kR)+\mathrm {bei} ^{2}(kR)}},\\[6pt]F_{2}(kr)&={\frac {\mathrm {ber} (kr)\mathrm {bei} (kR)-\mathrm {bei} (kr)\mathrm {ber} (kR)}{\mathrm {ber} ^{2}(kR)+\mathrm {bei} ^{2}(kR)}},\end{aligned}}

где $ber$ и $bei$ — функции Кельвина , а $k 2 = ⁠ ρω / μ ⁠$ .

Плоское течение Пуазейля

Плоское течение Пуазейля — это течение, возникающее между двумя бесконечно длинными параллельными пластинами, разделенными расстоянием $h,$ с постоянным градиентом давления $G = - ⁠ d p / d x ⁠$ наносится по направлению потока. Поток по существу однонаправленный из-за бесконечной длины. Уравнения Навье – Стокса сводятся к

{\frac {\mathrm {d} ^{2}u}{\mathrm {d} y^{2}}}=-{\frac {G}{\mu }}

с условием предотвращения скольжения на обеих стенках

u(0)=0,\quad u(h)=0

Следовательно, распределение скорости и объемный расход на единицу длины равны

u(y)={\frac {G}{2\mu }}y(h-y),\quad Q={\frac {Gh^{3}}{12\mu }}.

Течение Пуазейля через некоторые некруглые сечения.

Жозеф Буссинеск получил профиль скорости и объемный расход в 1868 году для прямоугольного канала и труб равностороннего треугольного поперечного сечения и для эллиптического поперечного сечения. ^[17] Джозеф Праудман вывел то же самое для равнобедренных треугольников в 1914 году. ^[18] Пусть $G = - ⁠ d p / d x ⁠$ — постоянный градиент давления, действующий в направлении, параллельном движению.

Скорость и объемный расход в прямоугольном канале высотой $0 \leq y \leq h$ и шириной $0 \leq z \leq l$ равны

{\begin{aligned}u(y,z)&={\frac {G}{2\mu }}y(h-y)-{\frac {4Gh^{2}}{\mu \pi ^{3}}}\sum _{n=1}^{\infty }{\frac {1}{(2n-1)^{3}}}{\frac {\sinh(\beta _{n}z)+\sinh[\beta _{n}(l-z)]}{\sinh(\beta _{n}l)}}\sin(\beta _{n}y),\quad \beta _{n}={\frac {(2n-1)\pi }{h}},\\[6pt]Q&={\frac {Gh^{3}l}{12\mu }}-{\frac {16Gh^{4}}{\pi ^{5}\mu }}\sum _{n=1}^{\infty }{\frac {1}{(2n-1)^{5}}}{\frac {\cosh(\beta _{n}l)-1}{\sinh(\beta _{n}l)}}.\end{aligned}}

Скорость и объемный расход трубки с равносторонним треугольным поперечным сечением с длиной стороны $⁠ 2 часа / \sqrt 3 ⁠$ есть

{\begin{aligned}u(y,z)&=-{\frac {G}{4\mu h}}(y-h)\left(y^{2}-3z^{2}\right),\\[6pt]Q&={\frac {Gh^{4}}{60{\sqrt {3}}\mu }}.\end{aligned}}

Скорость и объемный расход в прямоугольном равнобедренном треугольнике $y = π$ , $y \pm z = 0$ равны

{\begin{aligned}u(y,z)&={\frac {G}{2\mu }}(y+z)(\pi -y)-{\frac {G}{\pi \mu }}\sum _{n=1}^{\infty }{\frac {1}{\beta _{n}^{3}\sinh(2\pi \beta _{n})}}\left\{\sinh[\beta _{n}(2\pi -y+z)]\sin[\beta _{n}(y+z)]-\sinh[\beta _{n}(y+z)]\sin[\beta _{n}(y-z)]\right\},\quad \beta _{n}=n+{\tfrac {1}{2}},\\[6pt]Q&={\frac {G\pi ^{4}}{12\mu }}-{\frac {G}{2\pi \mu }}\sum _{n=1}^{\infty }{\frac {1}{\beta _{n}^{5}}}\left[\coth(2\pi \beta _{n})+\csc(2\pi \beta _{n})\right].\end{aligned}}

Распределение скорости для труб эллиптического сечения с полуосями $a$ и $b$ имеет вид ^[11]

{\begin{aligned}u(y,z)&={\frac {G}{2\mu \left({\frac {1}{a^{2}}}+{\frac {1}{b^{2}}}\right)}}\left(1-{\frac {y^{2}}{a^{2}}}-{\frac {z^{2}}{b^{2}}}\right),\\[6pt]Q&={\frac {\pi Ga^{3}b^{3}}{4\mu \left(a^{2}+b^{2}\right)}}.\end{aligned}}

Здесь, когда $a = b$ , восстанавливается поток Пуазейля для круглой трубы, а когда $a \to \infty$ , плоский поток Пуазейля восстанавливается . Также доступны более явные решения с поперечными сечениями, такие как сечения в форме улитки, сечения, имеющие форму круга с надрезом, следующего за полукругом, кольцевые сечения между гомофокальными эллипсами, кольцевые сечения между неконцентрическими кругами, как описано Ратипом Беркером [ tr ; де ] . ^[19]^[20]

Течение Пуазейля через произвольное сечение

Поток через произвольное сечение $u (y, z)$ удовлетворяет условию $u = 0$ на стенках. Основное уравнение сводится к ^[21]

{\frac {\partial ^{2}u}{\partial y^{2}}}+{\frac {\partial ^{2}u}{\partial z^{2}}}=-{\frac {G}{\mu }}.

Если мы введем новую зависимую переменную как

U=u+{\frac {G}{4\mu }}\left(y^{2}+z^{2}\right),

тогда легко видеть, что задача сводится к интегрированию уравнения Лапласа

{\frac {\partial ^{2}U}{\partial y^{2}}}+{\frac {\partial ^{2}U}{\partial z^{2}}}=0

удовлетворяющее условию

U={\frac {G}{4\mu }}\left(y^{2}+z^{2}\right)

на стене.

Уравнение Пуазейля для идеального изотермического газа.

Для сжимаемой жидкости в трубке объемный расход $Q (x)$ и осевая скорость не являются постоянными вдоль трубы; но массовый расход постоянен по длине трубки. Объемный расход обычно выражается через давление на выходе. Когда жидкость сжимается или расширяется, совершается работа, и жидкость нагревается или охлаждается. Это означает, что скорость потока зависит от передачи тепла к жидкости и от нее. Для идеального газа в изотермическом случае, когда температура жидкости может уравновеситься с окружающей средой, можно вывести приближенное соотношение для падения давления. ^[22] Используя уравнение состояния идеального газа для процесса с постоянной температурой (т.е. $p/\rho$ является постоянным) и сохранением массового расхода (т.е. ${\dot {m}}=\rho Q$ соотношение $Qp = Q 1 p 1 = Q 2 p 2$ постоянна), можно получить . На коротком участке трубы газ, текущий через трубу, можно считать несжимаемым, так что локально можно использовать закон Пуазейля:

-{\frac {\mathrm {d} p}{\mathrm {d} x}}={\frac {8\mu Q}{\pi R^{4}}}={\frac {8\mu Q_{2}p_{2}}{\pi pR^{4}}}\quad \Rightarrow \quad -p{\frac {\mathrm {d} p}{\mathrm {d} x}}={\frac {8\mu Q_{2}p_{2}}{\pi R^{4}}}.

Здесь мы предположили, что локальный градиент давления не слишком велик, чтобы оказывать какое-либо влияние на сжимаемость. Хотя локально мы игнорировали эффекты изменения давления из-за изменения плотности, на больших расстояниях эти эффекты принимаются во внимание. Поскольку $µ$ не зависит от давления, приведенное выше уравнение можно проинтегрировать по длине $L,$ чтобы получить

p_{1}^{2}-p_{2}^{2}={\frac {16\mu LQ_{2}p_{2}}{\pi R^{4}}}.

Следовательно, объемный расход на выходе из трубы определяется выражением

Q_{2}={\frac {\pi R^{4}}{16\mu L}}\left({\frac {p_{1}^{2}-p_{2}^{2}}{p_{2}}}\right)={\frac {\pi R^{4}\left(p_{1}-p_{2}\right)}{8\mu L}}{\frac {\left(p_{1}+p_{2}\right)}{2p_{2}}}.

Это уравнение можно рассматривать как закон Пуазейля с дополнительным поправочным коэффициентом. $⁠ p 1 + p 2 / 2 p 2 ⁠$ выражающее среднее давление относительно давления на выходе.

Аналогия электрических схем

Первоначально электричество считалось своего рода жидкостью. Эта гидравлическая аналогия по-прежнему концептуально полезна для понимания цепей. Эта аналогия также используется для изучения частотной характеристики гидромеханических сетей с использованием схемных инструментов, и в этом случае гидравлическая сеть называется гидравлической схемой . Закон Пуазейля соответствует закону Ома для электрических цепей, $V = IR$ . Поскольку результирующая сила, действующая на жидкость, равна $Δ F = S Δ p$ , где $S = π r 2$ , т.е. $Δ F = π r 2 ∆ P$ , то из закона Пуазейля следует, что

\Delta F={\frac {8\mu LQ}{r^{2}}}

.

Для электрических цепей пусть $n$ — концентрация свободных заряженных частиц (в м ⁻³) и пусть $q *$ — заряд каждой частицы (в кулонах ). (Для электронов $q * = e = 1,6 \times 10 -19 С.$ ) Тогда $nQ$ — число частиц в объёме $Q$ , а $nQq *$ — их суммарный заряд. заряд, протекающий через сечение в единицу времени, т. е. ток $I.$ Это Следовательно, $I = nQq *$ . Следовательно, $Q = ⁠ I / nq * ⁠$ и

\Delta F={\frac {8\mu LI}{nr^{2}q^{*}}}.

Но $∆ F = Eq$ , где $q$ — полный заряд в объёме трубки. Объем трубки равен $π r 2 L$ , поэтому число заряженных частиц в этом объеме равно $n π r 2 L$ , а их суммарный заряд $q = n π r 2 Лк *$ . Поскольку напряжение $V = EL$ , то

V={\frac {8\mu LI}{n^{2}\pi r^{4}\left(q^{*}\right)^{2}}}.

Это в точности закон Ома, где сопротивление $R = ⁠ V / I ⁠$ описывается формулой

R={\frac {8\mu L}{n^{2}\pi r^{4}\left(q^{*}\right)^{2}}}

.

Отсюда следует, что сопротивление $R$ пропорционально длине $L$ резистора, что верно. Однако отсюда также следует, что сопротивление $R$ обратно пропорционально четвертой степени радиуса $r$ , т.е. сопротивление $R$ обратно пропорционально второй степени площади поперечного сечения $S = π r. 2$ резистора, что отличается от электрической формулы. Электрическая зависимость сопротивления равна

R={\frac {\rho L}{S}},

где $ρ$ – удельное сопротивление; т.е. сопротивление $R$ обратно пропорционально площади поперечного сечения $S$ резистора. ^[23] Причина, по которой закон Пуазейля приводит к другой формуле сопротивления $R,$ заключается в разнице между потоком жидкости и электрическим током. Электронный газ невязкий , поэтому его скорость не зависит от расстояния до стенок проводника. Сопротивление возникает из-за взаимодействия между текущими электронами и атомами проводника. Следовательно, закон Пуазейля и гидравлическая аналогия полезны только в определенных пределах применительно к электричеству. И закон Ома, и закон Пуазейля иллюстрируют явления переноса .

Медицинские применения – внутривенный доступ и доставка жидкости

Уравнение Хагена-Пуазейля полезно для определения сосудистого сопротивления и, следовательно, скорости потока внутривенных (ВВ) жидкостей , чего можно достичь, используя периферические и центральные канюли различных размеров . Уравнение гласит, что скорость потока пропорциональна радиусу в четвертой степени, а это означает, что небольшое увеличение внутреннего диаметра канюли приводит к значительному увеличению скорости потока внутривенных жидкостей. Радиус внутривенных канюль обычно измеряется в «калибровке», которая обратно пропорциональна радиусу. Периферические внутривенные канюли обычно доступны в размерах (от больших до маленьких) 14G, 16G, 18G, 20G, 22G, 26G. Например, если предположить, что длины канюль равны, поток канюли 14G в 1,73 раза больше, чем у канюли 16G, и в 4,16 раза больше, чем у канюли 20G. В нем также говорится, что поток обратно пропорционален длине, а это означает, что более длинные линии имеют меньшую скорость потока. Это важно помнить, поскольку в экстренных ситуациях многие врачи отдают предпочтение более коротким и большим катетерам, а не более длинным и узким. Хотя это и имеет меньшее клиническое значение, повышенное изменение давления ( $∆ p$ ) — например, путем создания давления в мешке с жидкостью, сдавливания мешка или подвешивания мешка выше (относительно уровня канюли) — можно использовать для увеличения скорости потока. Также полезно понимать, что вязкие жидкости будут течь медленнее (например, при переливании крови ).

См. также

Цитированные ссылки

^ Jump up to: Перейти обратно: ^а ^б ^с Сутера, Сальваторе П.; Скалак, Ричард (1993). «История закона Пуазейля». Ежегодный обзор механики жидкости . 25 : 1–19. Бибкод : 1993АнРФМ..25....1С . дои : 10.1146/annurev.fl.25.010193.000245 .
^ Сабо, Иштван (1979). История принципов механики и их основные приложения . Базель: Birkhäuser Verlag.
^ Стоукс, Г.Г. (1845). «О теориях внутреннего трения движущихся жидкостей, равновесия и движения упругих тел». Труды Кембриджского философского общества . 8 : 287–341.
^ Jump up to: Перейти обратно: ^а ^б ^с "Давление" . гиперфизика.phy-astr.gsu.edu . Проверено 15 декабря 2019 г.
^ Кирби, Би Джей (2010). Микро- и наномасштабная механика жидкости: транспорт в микрофлюидных устройствах . Нью-Йорк: Издательство Кембриджского университета. ISBN 9780521119030 . OCLC 665837940 .
^ Брюус, Х. (2007). Теоретическая микрофлюидика .
^ Пфицнер, Дж. (1976). «Пуазей и его закон» (PDF) . Анестезия . 31 (2): 273–275. дои : 10.1111/j.1365-2044.1976.tb11804.x . ПМИД 779509 . S2CID 40607063 . Архивировано из оригинала (PDF) 10 августа 2017 г.
^ Фогель, Стивен (1981). Жизнь в движущихся жидкостях: физическая биология потока . Издательство PWS Кент. ISBN 0871507498 .
^ техническая наука (2 апреля 2020 г.). «Энергетический анализ закона Хагена – Пуазейля» . техническая наука . Проверено 7 мая 2020 г.
^ Детерминанты сопротивления кровеносных сосудов .
^ Jump up to: Перейти обратно: ^а ^б Бэтчелор, Джордж Кейт (2000). «Введение в гидродинамику» . Издательство Кембриджского университета . ISBN 9780521663960 .
^ Розенхед, Луи, изд. (1963). Ламинарные пограничные слои . Кларендон Пресс.
^ Сексл, Т. (1930). «О «кольцевом эффекте», открытом Э. Г. Ричардсоном ». Журнал физики . 61 (5–6): 349–362. Бибкод : 1930ZPhy...61..349S . дои : 10.1007/BF01340631 . S2CID 119771908 .
^ Ламбосси, П. (1952). «Вынужденные колебания несжимаемой и вязкой жидкости в жесткой и горизонтальной трубе. Расчет силы трения». Хелв. Физ. Акта . 25 : 371–386.
^ Уомерсли, младший (1955). «Метод расчета скорости, скорости кровотока и вязкого сопротивления в артериях при известном градиенте давления» . Журнал физиологии . 127 (3): 553–563. дои : 10.1113/jphysicalol.1955.sp005276 . ПМЦ 1365740 . ПМИД 14368548 .
^ Учида, С. (1956). «Пульсирующий вязкий поток, наложенный на устойчивое ламинарное движение несжимаемой жидкости в круглой трубе». Журнал прикладной математики и физики . 7 (5): 403–422. Бибкод : 1956ЗаМП....7..403У . дои : 10.1007/BF01606327 . S2CID 123217023 .
^ Буссинеск, Жозеф (1868). «Память о влиянии трения при регулярном движении жидкостей». Дж. Математика. Чистое приложение . 13 (2): 377–424.
^ Праудман, Дж. (1914). «Заметки о движении вязких жидкостей в каналах» . Лондонский, Эдинбургский и Дублинский философский журнал и научный журнал . 28 (163): 30–36. дои : 10.1080/14786440708635179 .
^ Беркер, Р. (1963). «Интегрирование уравнений движения вязкой несжимаемой жидкости». Handbuch der Physik . Полет. 3.стр. 1–384.
^ Дразин, Филип Г .; Райли, Норман (2006). Уравнения Навье–Стокса: классификация течений и точные решения . Том. № 334. Издательство Кембриджского университета. ISBN 9780521681629 . {{cite book}}: |volume= есть дополнительный текст ( помощь )
^ Керл, Сэмюэл Ньюби ; Дэвис, HJ (1971). Современная гидродинамика . Том. 1. Несжимаемый поток. Ван Ностранд Рейнхольд.
^ Ландау, LD ; Лифшиц, Э.М. (1987). Механика жидкости . Пергамон Пресс. п. 55, задача 6. ISBN 0-08-033933-6 .
^ Фюттерер, К.; и др. (2004). «Система впрыска и регулирования расхода микроканалов». Лаборатория на чипе . 4 (4): 351–356. дои : 10.1039/B316729A . ПМИД 15269803 .

Ссылки

Сутера, СП; Скалак, Р. (1993). «История закона Пуазейля». Ежегодный обзор механики жидкости . 25 : 1–19. Бибкод : 1993АнРФМ..25....1С . дои : 10.1146/annurev.fl.25.010193.000245 . .
Пфицнер, Дж (1976). «Пуазей и его закон». Анестезия . Том. 31, нет. 2 (опубликовано в марте 1976 г.). стр. 273–5. дои : 10.1111/j.1365-2044.1976.tb11804.x . ПМИД 779509 . .
Беннетт, Колорадо; Майерс, Дж. Э. (1962). Импульс, тепло и массоперенос . МакГроу-Хилл. .

Внешние ссылки

[hist-1] Jump up to: Перейти обратно: ^а ^б ^с Сутера, Сальваторе П.; Скалак, Ричард (1993). «История закона Пуазейля». Ежегодный обзор механики жидкости . 25 : 1–19. Бибкод : 1993АнРФМ..25....1С . дои : 10.1146/annurev.fl.25.010193.000245 .

[2] Сабо, Иштван (1979). История принципов механики и их основные приложения . Базель: Birkhäuser Verlag.

[3] Стоукс, Г.Г. (1845). «О теориях внутреннего трения движущихся жидкостей, равновесия и движения упругих тел». Труды Кембриджского философского общества . 8 : 287–341.

[:0-4] Jump up to: Перейти обратно: ^а ^б ^с "Давление" . гиперфизика.phy-astr.gsu.edu . Проверено 15 декабря 2019 г.

[Kirby-5] Кирби, Би Джей (2010). Микро- и наномасштабная механика жидкости: транспорт в микрофлюидных устройствах . Нью-Йорк: Издательство Кембриджского университета. ISBN 9780521119030 . OCLC 665837940 .

[Bruus-6] Брюус, Х. (2007). Теоретическая микрофлюидика .

[7] Пфицнер, Дж. (1976). «Пуазей и его закон» (PDF) . Анестезия . 31 (2): 273–275. дои : 10.1111/j.1365-2044.1976.tb11804.x . ПМИД 779509 . S2CID 40607063 . Архивировано из оригинала (PDF) 10 августа 2017 г.

[8] Фогель, Стивен (1981). Жизнь в движущихся жидкостях: физическая биология потока . Издательство PWS Кент. ISBN 0871507498 .

[9] техническая наука (2 апреля 2020 г.). «Энергетический анализ закона Хагена – Пуазейля» . техническая наука . Проверено 7 мая 2020 г.

[10] Детерминанты сопротивления кровеносных сосудов .

[Batchelor,_George_Keith_2000-11] Jump up to: Перейти обратно: ^а ^б Бэтчелор, Джордж Кейт (2000). «Введение в гидродинамику» . Издательство Кембриджского университета . ISBN 9780521663960 .

[12] Розенхед, Луи, изд. (1963). Ламинарные пограничные слои . Кларендон Пресс.

[13] Сексл, Т. (1930). «О «кольцевом эффекте», открытом Э. Г. Ричардсоном ». Журнал физики . 61 (5–6): 349–362. Бибкод : 1930ZPhy...61..349S . дои : 10.1007/BF01340631 . S2CID 119771908 .

[14] Ламбосси, П. (1952). «Вынужденные колебания несжимаемой и вязкой жидкости в жесткой и горизонтальной трубе. Расчет силы трения». Хелв. Физ. Акта . 25 : 371–386.

[15] Уомерсли, младший (1955). «Метод расчета скорости, скорости кровотока и вязкого сопротивления в артериях при известном градиенте давления» . Журнал физиологии . 127 (3): 553–563. дои : 10.1113/jphysicalol.1955.sp005276 . ПМЦ 1365740 . ПМИД 14368548 .

[16] Учида, С. (1956). «Пульсирующий вязкий поток, наложенный на устойчивое ламинарное движение несжимаемой жидкости в круглой трубе». Журнал прикладной математики и физики . 7 (5): 403–422. Бибкод : 1956ЗаМП....7..403У . дои : 10.1007/BF01606327 . S2CID 123217023 .

[17] Буссинеск, Жозеф (1868). «Память о влиянии трения при регулярном движении жидкостей». Дж. Математика. Чистое приложение . 13 (2): 377–424.

[18] Праудман, Дж. (1914). «Заметки о движении вязких жидкостей в каналах» . Лондонский, Эдинбургский и Дублинский философский журнал и научный журнал . 28 (163): 30–36. дои : 10.1080/14786440708635179 .

[19] Беркер, Р. (1963). «Интегрирование уравнений движения вязкой несжимаемой жидкости». Handbuch der Physik . Полет. 3.стр. 1–384.

[20] Дразин, Филип Г .; Райли, Норман (2006). Уравнения Навье–Стокса: классификация течений и точные решения . Том. № 334. Издательство Кембриджского университета. ISBN 9780521681629 . {{cite book}}: |volume= есть дополнительный текст ( помощь )

[21] Керл, Сэмюэл Ньюби ; Дэвис, HJ (1971). Современная гидродинамика . Том. 1. Несжимаемый поток. Ван Ностранд Рейнхольд.

[22] Ландау, LD ; Лифшиц, Э.М. (1987). Механика жидкости . Пергамон Пресс. п. 55, задача 6. ISBN 0-08-033933-6 .

[23] Фюттерер, К.; и др. (2004). «Система впрыска и регулирования расхода микроканалов». Лаборатория на чипе . 4 (4): 351–356. дои : 10.1039/B316729A . ПМИД 15269803 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]