Эффект Джоуля – Томсона

«Процесс регулирования» перенаправляется сюда. О концепции вычислений см. в разделе «Ограничение скорости» .

В термодинамике эффект Джоуля -Томсона (также известный как эффект Джоуля-Кельвина или эффект Кельвина-Джоуля ) описывает изменение температуры реального газа или жидкости (в отличие от идеального газа ), когда он подвергается воздействию разницы давлений через клапан , сохраняя при этом ее изоляцию , или пористую пробку чтобы исключить обмен тепла с окружающей средой. Эта процедура называется процессом дросселирования или процессом Джоуля-Томсона . Эффект является чисто эффектом отклонения от идеальности, поскольку любой идеальный газ не имеет эффекта JT.

При комнатной температуре все газы, кроме водорода , гелия и неона, охлаждаются при расширении в результате процесса Джоуля-Томсона при дросселировании через отверстие; температура этих трех газов повышается при прохождении через пористую пробку при комнатной температуре, но температура снижается, когда уже при более низких температурах. Большинство жидкостей, таких как гидравлические масла, нагреваются в результате дросселирования Джоуля-Томсона. Температура, при которой эффект ДТ меняет знак, является температурой инверсии .

Процесс дросселирования при охлаждении газа обычно используется в процессах охлаждения, таких как ожижители в промышленных процессах разделения воздуха . В гидравлике эффект потепления от дросселирования Джоуля-Томсона можно использовать для обнаружения клапанов с внутренними утечками, поскольку они выделяют тепло, которое можно обнаружить с помощью термопары или тепловизионной камеры . Регулирование – это принципиально необратимый процесс . Дросселирование из-за гидравлического сопротивления в питающих линиях, теплообменниках, регенераторах и других узлах (тепловых) машин является источником потерь, ограничивающих их производительность.

Поскольку это процесс с постоянной энтальпией, его можно использовать для экспериментального измерения линий постоянной энтальпии (изентальп) на $(p,T)$ схема газа. В сочетании с удельной теплоемкостью при постоянном давлении $c_{P}=(\partial h/\partial T)_{P}$ он позволяет полностью измерить термодинамический потенциал газа.

История

Эффект назван в честь Джеймса Прескотта Джоуля и Уильяма Томсона, 1-го барона Кельвина , которые открыли его в 1852 году. Он последовал за более ранней работой Джоуля о джоулевом расширении , в которой газ подвергается свободному расширению в вакууме , а температура не меняется, если газ идеальный .

Описание

Адиабатическое ( без теплообмена) расширение газа может осуществляться несколькими способами. Изменение температуры, испытываемое газом при расширении, зависит не только от начального и конечного давления, но и от способа осуществления расширения.

• Если процесс расширения обратим , то есть газ все время находится в термодинамическом равновесии , это называется изоэнтропическим расширением. В этом сценарии газ совершает положительную работу , и его температура снижается. при расширении
• С другой стороны, при свободном расширении газ не совершает работы и не поглощает тепло, поэтому внутренняя энергия сохраняется. При таком расширении температура идеального газа останется постоянной, но температура реального газа уменьшится, за исключением очень высоких температур.
• Обсуждаемый в этой статье метод расширения, при котором газ или жидкость при давлении P ₁ перетекает в область более низкого давления P ₂ без существенного изменения кинетической энергии, называется расширением Джоуля-Томсона. Расширение по своей сути необратимо. Во время этого расширения энтальпия остается неизменной (см. доказательство ниже). В отличие от свободного расширения совершается работа, вызывающая изменение внутренней энергии. Увеличение или уменьшение внутренней энергии определяется тем, совершается ли работа над жидкостью или с помощью нее; что определяется начальным и конечным состояниями расширения и свойствами жидкости.

Знак коэффициента Джоуля – Томсона, $\mu _{\mathrm {JT} }$ для N ₂ . В области, ограниченной красной линией, расширение Джоуля – Томсона приводит к охлаждению ( $\mu _{\mathrm {JT} }>0$); за пределами этой области расширение приводит к нагреву. Кривая сосуществования газа и жидкости показана синей линией, заканчивающейся в критической точке (сплошной синий круг). Штриховыми линиями обозначена область, где N ₂ является сверхкритической жидкостью (где свойства плавно переходят от жидкоподобных к газообразным).

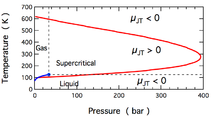
Изменение температуры, возникающее во время расширения Джоуля-Томсона, количественно выражается коэффициентом Джоуля-Томсона , $\mu _{\mathrm {JT} }$. Этот коэффициент может быть как положительным (соответствующим охлаждению), так и отрицательным (нагреву); области, где каждый из них встречается для молекулярного азота N ₂ , показаны на рисунке. Обратите внимание, что большинство условий на рисунке соответствует тому, что N ₂ является сверхкритической жидкостью , где он обладает некоторыми свойствами газа и некоторыми свойствами жидкости, но на самом деле не может быть описан как ни то, ни другое. Коэффициент отрицателен как при очень высоких, так и при очень низких температурах; при очень высоком давлении он отрицателен при всех температурах. Максимальная температура инверсии (621 К для N ₂ ) происходит при приближении к нулевому давлению. Для газа N ₂ при низких давлениях $\mu _{\mathrm {JT} }$ отрицательна при высоких температурах и положительна при низких температурах. газ-жидкость При температурах ниже кривой сосуществования N ₂ конденсируется с образованием жидкости и коэффициент снова становится отрицательным. Таким образом, для газа N ₂ ниже 621 К расширение Джоуля-Томсона можно использовать для охлаждения газа до образования жидкого N ₂ .

Физический механизм

Есть два фактора, которые могут изменить температуру жидкости во время адиабатического расширения: изменение внутренней энергии или преобразование потенциальной и кинетической внутренней энергии. Температура является мерой тепловой кинетической энергии (энергии, связанной с движением молекул); поэтому изменение температуры указывает на изменение тепловой кинетической энергии. Внутренняя энергия представляет собой сумму тепловой кинетической энергии и тепловой потенциальной энергии. Таким образом, даже если внутренняя энергия не меняется, температура может измениться за счет преобразования кинетической и потенциальной энергии; это то, что происходит при свободном расширении и обычно приводит к снижению температуры по мере расширения жидкости. Если при расширении жидкости совершается работа, то полная внутренняя энергия изменяется. Именно это происходит при расширении Джоуля-Томсона и может вызывать больший нагрев или охлаждение, чем наблюдается при свободном расширении.

В расширении Джоуля – Томсона энтальпия остается постоянной. Энтальпия, $H$, определяется как

$H=U+PV$

где $U$ внутренняя энергия, $P$ это давление, и $V$ это объем. В условиях разложения Джоуля–Томсона изменение $PV$ представляет работу, совершенную жидкостью (см. доказательство ниже). Если $PV$ увеличивается, с $H$ константа, тогда $U$ должно уменьшаться в результате совершения жидкостью работы над окружающей средой. Это вызывает понижение температуры и приводит к положительному коэффициенту Джоуля – Томсона. И наоборот, снижение $PV$ означает, что над жидкостью совершается работа и внутренняя энергия увеличивается. Если увеличение кинетической энергии превышает увеличение потенциальной энергии, произойдет повышение температуры жидкости и коэффициент Джоуля-Томсона станет отрицательным.

Для идеального газа $PV$ не меняется при расширении Джоуля – Томсона. В результате внутренняя энергия не изменяется; поскольку также нет изменения тепловой потенциальной энергии, не может быть и изменения тепловой кинетической энергии и, следовательно, никакого изменения температуры. В реальных газах $PV$ меняется.

Соотношение стоимости $PV$ относительно ожидаемого для идеального газа при той же температуре, называется коэффициентом сжимаемости , $Z$. Для газа это значение обычно меньше единицы при низкой температуре и больше единицы при высокой температуре (см. обсуждение коэффициента сжимаемости ). При низком давлении значение $Z$ всегда движется к единице по мере расширения газа. Таким образом, при низкой температуре $Z$ и $PV$ будет увеличиваться по мере расширения газа, что приводит к положительному коэффициенту Джоуля – Томсона. При высокой температуре, $Z$ и $PV$ уменьшаться по мере расширения газа; если уменьшение достаточно велико, коэффициент Джоуля – Томсона будет отрицательным.

Для жидкостей и сверхкритических жидкостей под высоким давлением $PV$ увеличивается по мере увеличения давления. Это происходит из-за того, что молекулы сближаются, так что объем едва может уменьшиться из-за более высокого давления. В таких условиях коэффициент Джоуля-Томсона отрицательный, как видно на рисунке выше .

Физический механизм, связанный с эффектом Джоуля-Томсона, тесно связан с механизмом ударной волны . хотя ударная волна отличается тем, что изменение объемной кинетической энергии газового потока немаловажно.

Коэффициент Джоуля-Томсона (Кельвина)

Рис. 1 – Коэффициенты Джоуля–Томсона для различных газов при атмосферном давлении

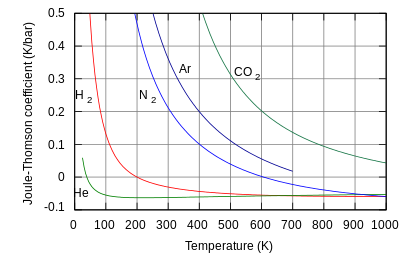
Скорость изменения температуры $T$ что касается давления $P$ в процессе Джоуля – Томсона (т.е. при постоянной энтальпии $H$) — коэффициент Джоуля–Томсона (Кельвина). $\mu _{\mathrm {JT} }$. Этот коэффициент можно выразить через удельный объем газа. $V$, его теплоемкость при постоянном давлении $C_{\mathrm {p} }$, и его коэффициент теплового расширения $\alpha$ как:

$\mu _{\mathrm {JT} }=\left({\partial T \over \partial P}\right)_{H}={\frac {V}{C_{\mathrm {p} }}}(\alpha T-1)\,$

см. в § Вывод коэффициента Джоуля – Томсона Доказательство этого соотношения ниже. Стоимость $\mu _{\mathrm {JT} }$ обычно выражается в °C/ бар (единицы СИ: К / Па ) и зависит от типа газа, а также от температуры и давления газа до расширения. Его зависимость от давления обычно составляет всего несколько процентов для давлений до 100 бар.

Все реальные газы имеют точку инверсии , в которой значение $\mu _{\mathrm {JT} }$ меняет знак. Температура этой точки, температура инверсии Джоуля – Томсона , зависит от давления газа перед расширением.

При расширении газа давление уменьшается, поэтому знак $\partial P$ является отрицательным по определению. Имея это в виду, в следующей таблице объясняется, когда эффект Джоуля-Томсона охлаждает или нагревает реальный газ:

Если температура газа	затем $\mu _{\text{JT}}$ является	с $\partial P$ является	таким образом $\partial T$ должно быть	итак, газ
ниже температуры инверсии	позитивный	всегда отрицательный	отрицательный	охлаждает
выше температуры инверсии	отрицательный		позитивный	согревает

Гелий и водород - это два газа, температура инверсии Джоуля-Томсона которых при давлении в одну атмосферу очень низка (например, около 40 К, -233 ° C для гелия). Таким образом, гелий и водород нагреваются при расширении при постоянной энтальпии и обычных комнатных температурах. С другой стороны, азот и кислород , два наиболее распространенных газа в воздухе, имеют температуры инверсии 621 К (348 °С) и 764 К (491 °С) соответственно: эти газы можно охладить от комнатной температуры с помощью силы Джоуля– Эффект Томсона.

Для идеального газа $\mu _{\text{JT}}$ всегда равен нулю: идеальные газы не нагреваются и не охлаждаются при расширении с постоянной энтальпией.

Теоретические модели

Для газа Дитеричи связь между пониженным давлением и пониженной температурой инверсии равна ${\tilde {p}}=(8-{\tilde {T}}_{I})e^{{\frac {5}{2}}-{\frac {4}{8-{\tilde {T}}_{I}}}}$. Воспроизведено с рис. 17 .

Для газа Ван-дер-Ваальса коэффициент равен $$\mu _{\text{JT}}=-{\frac {V_{m}}{C_{p}}}{\frac {RTV_{m}^{2}b-2a(V_{m}-b)^{2}}{RTV_{m}^{3}-2a(V_{m}-b)^{2}}}.$$с температурой инверсии ${\frac {2a}{bR}}\left(1-{\frac {b}{V_{m}}}\right)^{2}$.

Для газа Дитеричи приведенная температура инверсии равна ${\tilde {T}}_{I}=8-4/{\tilde {V}}_{m}$, а связь между приведенным давлением и приведенной температурой инверсии равна ${\tilde {p}}=(8-{\tilde {T}}_{I})e^{{\frac {5}{2}}-{\frac {4}{8-{\tilde {T}}_{I}}}}$. Это нарисовано справа. Критическая точка приходится на область, где газ охлаждается при расширении. Внешняя область — это место, где газ нагревается при расширении.

Приложения

На практике эффект Джоуля-Томсона достигается за счет расширения газа через дросселирующее устройство (обычно клапан ), которое должно быть очень хорошо изолировано, чтобы предотвратить любую передачу тепла к газу или от него. Во время расширения газ не извлекает никакой внешней работы ( газ нельзя расширять с помощью турбины например, ).

Охлаждение, возникающее при расширении Джоуля-Томсона, делает его ценным инструментом в охлаждении . Эффект применяется в методе Линде как стандартный процесс в нефтехимической промышленности , где эффект охлаждения используется для сжижения газов , а также во многих криогенных приложениях (например, для производства жидкого кислорода, азота и аргона ). Для сжижения газа по циклу Линде газ должен иметь температуру ниже температуры инверсии. По этой причине простые ожижители с циклом Линде, начиная с температуры окружающей среды, не могут использоваться для сжижения гелия, водорода или неона . Сначала их необходимо охладить до температур инверсии, которые составляют -233°С (гелий), -71°С (водород) и -42°С (неон).

Доказательство того, что удельная энтальпия остается постоянной

В термодинамике так называемые «удельные» величины представляют собой количества на единицу массы (кг) и обозначаются строчными буквами. Итак, h , u и v — это удельная энтальпия , удельная внутренняя энергия и удельный объем (объем на единицу массы или обратная плотность) соответственно. В процессе Джоуля-Томсона удельная энтальпия h остается постоянной. Чтобы доказать это, первым делом нужно вычислить чистую работу, совершаемую при m движении массы газа через пробку. Это количество газа имеет объем V ₁ = m v ₁ в области давления P ₁ (область 1) и объем V ₂ = m v ₂ в области давления P ₂ (область 2). Тогда в области 1 «работа потока», совершаемая над количеством газа остальным газом, равна: W ₁ = m P ₁ v ₁ . В области 2 работа, совершаемая количеством газа над остальным газом, равна: W ₂ = m P ₂ v ₂ . Итак, полная работа, совершенная над массой m газа, равна

$W=mP_{1}v_{1}-mP_{2}v_{2}.$

Изменение внутренней энергии за вычетом полной работы, совершенной над количеством газа, согласно первому закону термодинамики , есть общее количество тепла, переданное этому количеству газа.

$U-W=Q$

В процессе Джоуля-Томсона газ изолирован, поэтому тепло не поглощается. Это означает, что

${\begin{aligned}(mu_{2}-mu_{1})&-(mP_{1}v_{1}-mP_{2}v_{2})=0\\mu_{1}+mP_{1}v_{1}&=mu_{2}+mP_{2}v_{2}\\u_{1}+P_{1}v_{1}&=u_{2}+P_{2}v_{2}\end{aligned}}$

где u ₁ и u ₂ обозначают удельную внутреннюю энергию газа в областях 1 и 2 соответственно. Используя определение удельной энтальпии h = u + Pv , из приведенного выше уравнения следует, что

$h_{1}=h_{2}$

где h ₁ и h ₂ обозначают удельные энтальпии количества газа в областях 1 и 2 соответственно.

Дросселирование на Т - s -диаграмме

Рис. 2 – Т - s диаграмма азота. Красный купол представляет собой двухфазную область со стороной с низкой энтропией (насыщенная жидкость) и стороной с высокой энтропией (насыщенный газ). Черные кривые показывают зависимость T - s вдоль изобар. Давление указано в барах. Синие кривые — изэнтальпы (кривые постоянной удельной энтальпии). Удельные энтальпии указаны в кДж/кг. Конкретные пункты a, b и т. д. рассматриваются в основном тексте.

Очень удобный способ получить количественное представление о процессе регулирования — использовать такие диаграммы, как h - T диаграммы , диаграммы h - P и другие. Обычно используются так называемые Т - s- диаграммы. приведена Т - s -диаграмма азота. На рис. 2 в качестве примера Различные точки обозначаются следующим образом:

1. Т = 300   К, р = 200 бар, s = 5,16   кДж/(кгК), h = 430   кДж/кг;
2. Т = 270   К, р = 1 бар, s = 6,79   кДж/(кгК), h = 430   кДж/кг;
3. Т = 133   К, р = 200 бар, s = 3,75   кДж/(кгК), h = 150   кДж/кг;
4. Т = 77,2   К, p = 1 бар, s = 4,40   кДж/(кгК), h = 150   кДж/кг;
5. Т = 77,2   К, p = 1 бар, s = 2,83   кДж/(кгК), h = 28   кДж/кг (насыщенная жидкость при 1 бар);
6. Т = 77,2   К, p = 1 бар, s = 5,41   кДж/(кгК), h = 230   кДж/кг (насыщенный газ при 1 бар).

Как было показано ранее, регулирование сохраняет h постоянным. Например, дросселирование от 200 бар и 300   К (точка а на рис. 2) соответствует изоэнтальпии (линии постоянной удельной энтальпии) 430   кДж/кг. При давлении 1 бар это приводит к точке b, температура которой составляет 270   К. Таким образом, регулирование давления с 200 бар до 1 бар приводит к охлаждению от комнатной температуры до температуры ниже точки замерзания воды. Дросселирование от 200 бар и начальной температуры 133   К (точка в на рис. 2) до 1 бар приводит к точке d, которая находится в двухфазной области азота при температуре 77,2   К. Поскольку энтальпия представляет собой экстенсивный параметр энтальпия в d ( h _d ) равна энтальпии в e ( h _e ), умноженной на массовую долю жидкости в d ( x _d ), плюс энтальпия в f ( h _f ), умноженная на массовую долю жидкости газ в d (1 - x _d ). Так

$h_{d}=x_{d}h_{e}+(1-x_{d})h_{f}.$

С числами: 150 = x _d 28 + (1 − x _d ) 230, поэтому x _d составляет около 0,40. Это означает, что массовая доля жидкости в газожидкостной смеси, выходящей из дроссельного клапана, составляет 40%.

Вывод коэффициента Джоуля–Томсона.

Трудно физически представить, что такое коэффициент Джоуля-Томсона, $\mu _{\mathrm {JT} }$, представляет. Кроме того, современные определения $\mu _{\mathrm {JT} }$ не используйте оригинальный метод Джоуля и Томсона, а вместо этого измеряйте другую, тесно связанную величину. Таким образом, полезно установить связи между $\mu _{\mathrm {JT} }$ и другие, более удобно измеряемые величины, как описано ниже.

что коэффициент Джоуля–Томсона включает три переменные T , P и H. Первый шаг в получении этих результатов — отметить , Полезный результат сразу получается при применении правила цикличности ; в терминах этих трех переменных это правило можно записать

$\left({\frac {\partial T}{\partial P}}\right)_{H}\left({\frac {\partial H}{\partial T}}\right)_{P}\left({\frac {\partial P}{\partial H}}\right)_{T}=-1.$

Каждая из трех частных производных в этом выражении имеет определенное значение. Первое - это $\mu _{\mathrm {JT} }$, второй – теплоемкость при постоянном давлении , $C_{\mathrm {p} }$, определяемый

$C_{\mathrm {p} }=\left({\frac {\partial H}{\partial T}}\right)_{P}$

и третий — обратный изотермическому коэффициенту Джоуля–Томсона , $\mu _{\mathrm {T} }$, определяемый

$\mu _{\mathrm {T} }=\left({\frac {\partial H}{\partial P}}\right)_{T}$.

Эту последнюю величину легче измерить, чем $\mu _{\mathrm {JT} }$ . Таким образом, выражение из циклического правила принимает вид

$\mu _{\mathrm {JT} }=-{\frac {\mu _{\mathrm {T} }}{C_{p}}}.$

Это уравнение можно использовать для получения коэффициентов Джоуля-Томсона из более легко измеряемого изотермического коэффициента Джоуля-Томсона. Далее он используется для получения математического выражения коэффициента Джоуля – Томсона через объемные свойства жидкости.

Если идти дальше, отправной точкой является фундаментальное уравнение термодинамики в терминах энтальпии; Это

$\mathrm {d} H=T\mathrm {d} S+V\mathrm {d} P.$

Теперь «деление» на d P при сохранении постоянной температуры дает

$\left({\frac {\partial H}{\partial P}}\right)_{T}=T\left({\frac {\partial S}{\partial P}}\right)_{T}+V$

Частная производная слева представляет собой изотермический коэффициент Джоуля – Томсона: $\mu _{\mathrm {T} }$, а тот, что справа, может быть выражен через коэффициент теплового расширения через соотношение Максвелла . Соответствующее отношение

$\left({\frac {\partial S}{\partial P}}\right)_{T}=-\left({\frac {\partial V}{\partial T}}\right)_{P}=-V\alpha \,$

где α — кубический коэффициент теплового расширения . Замена этих двух частных производных дает

$\mu _{\mathrm {T} }=-TV\alpha \ +V.$

Это выражение теперь может заменить $\mu _{\mathrm {T} }$ в предыдущем уравнении для $\mu _{\mathrm {JT} }$ чтобы получить:

$\mu _{\mathrm {JT} }\equiv \left({\frac {\partial T}{\partial P}}\right)_{H}={\frac {V}{C_{\mathrm {p} }}}(\alpha T-1).\,$

Это дает выражение для коэффициента Джоуля-Томсона через общедоступные свойства: теплоемкость, мольный объем и коэффициент теплового расширения. Это показывает, что температура инверсии Джоуля–Томсона, при которой $\mu _{\mathrm {JT} }$ равен нулю, возникает, когда коэффициент теплового расширения равен обратной величине температуры. Поскольку для идеальных газов это верно при всех температурах (см. Разложение по газам ), коэффициент Джоуля – Томсона идеального газа равен нулю при всех температурах.

Второй закон Джоуля

Смотрите также: первый закон Джоуля

Легко проверить, что для идеального газа, определенного подходящими микроскопическими постулатами, αT = 1, поэтому изменение температуры такого идеального газа при расширении Джоуля – Томсона равно нулю.Для такого идеального газа этот теоретический результат означает, что:

Внутренняя энергия фиксированной массы идеального газа зависит только от его температуры (а не давления или объема).

Это правило было первоначально обнаружено Джоулем экспериментально для реальных газов и известно как второй закон Джоуля . Более тонкие эксперименты обнаружили важные отклонения от него.

См. также

• Критическая точка (термодинамика)
• Энтальпия и изентальпийский процесс
• Идеальный газ
• Сжижение газов
• MIRI (прибор среднего инфракрасного диапазона) , петля J – T используется на одном из инструментов космического телескопа Джеймса Уэбба.
• Охлаждение
• Обратимый процесс (термодинамика)

Библиография

• М.В. Земанский (1968). Теплота и термодинамика; Учебник для среднего уровня . МакГроу-Хилл. стр. 182 , 355. LCCN   67026891 .
• Д.В. Шредер (2000). Введение в теплофизику . Эддисон Уэсли Лонгман. п. 142 . ISBN  978-0-201-38027-9 .
• К. Киттель, Х. Кремер (1980). Теплофизика . У. Х. Фриман. ISBN  978-0-7167-1088-2 .

Внешние ссылки

• Вайсштейн, Эрик Вольфганг (ред.). «Процесс Джоуля-Томсона» . Мир Науки .
• Вайсштейн, Эрик Вольфганг (ред.). «Коэффициент Джоуля-Томсона» . Мир Науки .
• «Кривая инверсии эффекта Джоуля-Томсона с использованием CEOS Пенга-Робинсона» . Демонстрационные проекты Wolfram Mathematica .
• Модуль эффекта Джоуля-Томсона , Университет Нотр-Дам