Изэнтропический процесс

Изэнтропический процесс — это идеализированный термодинамический процесс , который является одновременно адиабатическим и обратимым . Передача работы в системе происходит без трения , и нет чистой передачи тепла или вещества . Такой идеализированный процесс полезен в технике как модель и основа сравнения реальных процессов. Этот процесс идеализирован, поскольку в действительности обратимых процессов не происходит; представление о процессе как об адиабатическом и обратимом показало бы, что начальная и конечная энтропии одинаковы, поэтому его называют изэнтропическим (энтропия не меняется). Термодинамические процессы называются в зависимости от эффекта, который они оказывают на систему (например, изоволюметрический: постоянный объем, изоэнтальпический: постоянная энтальпия). Хотя на самом деле осуществить изэнтропический процесс не обязательно возможно, некоторые из них можно аппроксимировать как таковые.

Слово «изоэнтропический» происходит от названия процесса, при котором энтропия системы остается неизменной. В дополнение к процессу, который является одновременно адиабатическим и обратимым, это может также происходить в системе, где работа, совершаемая в системе, включает в себя внутреннее трение , и из системы отводится тепло, достаточное для его компенсации, чтобы оставить энтропия не изменилась. Однако по отношению к Вселенной ее энтропия в результате увеличится, в соответствии со Вторым законом термодинамики .

Фон

Второй закон термодинамики гласит: что

$T_{\text{surr}}dS\geq \delta Q,$

где $\delta Q$ - количество энергии, которую система получает при нагревании, $T_{\text{surr}}$температура а окружающей среды, $dS$ это изменение энтропии. Знак равенства относится к обратимому процессу , который представляет собой воображаемый идеализированный теоретический предел, никогда на самом деле не встречающийся в физической реальности, с практически одинаковыми температурами системы и окружающей среды. Для изэнтропического процесса, если он еще и обратим, передача энергии в виде тепла не происходит, поскольку процесс адиабатический ; δQ = 0. Напротив, если процесс необратим, внутри системы производится энтропия; следовательно, для поддержания постоянной энтропии внутри системы энергия должна одновременно отводиться из системы в виде тепла.

Для обратимых процессов изэнтропическое преобразование осуществляется путем термической «изоляции» системы от окружающей среды. Температура является термодинамической сопряженной переменной с энтропией, поэтому сопряженный процесс будет изотермическим процессом , в котором система термически «соединена» с тепловой баней с постоянной температурой.

Изэнтропические процессы в термодинамических системах

Диаграмма T – s (энтропия от температуры) изэнтропического процесса, представляющая собой отрезок вертикальной линии.

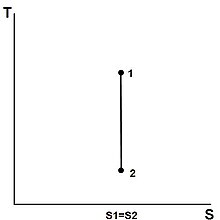
Энтропия данной массы не меняется в ходе процесса, который является внутренне обратимым и адиабатическим. Процесс, во время которого энтропия остается постоянной, называется изэнтропическим процессом, обозначаемым $\Delta s=0$ или $s_{1}=s_{2}$. Некоторыми примерами теоретически изэнтропических термодинамических устройств являются насосы , газовые компрессоры , турбины , сопла и диффузоры .

Изэнтропические КПД стационарных устройств в термодинамических системах

Большинство устройств с установившимся потоком работают в адиабатических условиях, и идеальным процессом для этих устройств является изэнтропический процесс. Параметр, который описывает, насколько эффективно устройство приближается к соответствующему изэнтропическому устройству, называется изэнтропическим или адиабатическим КПД.

Изэнтропический КПД турбин:

$\eta _{\text{t}}={\frac {\text{actual turbine work}}{\text{isentropic turbine work}}}={\frac {W_{a}}{W_{s}}}\cong {\frac {h_{1}-h_{2a}}{h_{1}-h_{2s}}}.$

Изэнтропический КПД компрессоров:

$\eta _{\text{c}}={\frac {\text{isentropic compressor work}}{\text{actual compressor work}}}={\frac {W_{s}}{W_{a}}}\cong {\frac {h_{2s}-h_{1}}{h_{2a}-h_{1}}}.$

Изэнтропический КПД форсунок:

$\eta _{\text{n}}={\frac {\text{actual KE at nozzle exit}}{\text{isentropic KE at nozzle exit}}}={\frac {V_{2a}^{2}}{V_{2s}^{2}}}\cong {\frac {h_{1}-h_{2a}}{h_{1}-h_{2s}}}.$

Для всех приведенных выше уравнений:

$h_{1}$ - удельная энтальпия на входе,

$h_{2a}$ - удельная энтальпия на выходе реального процесса,

$h_{2s}$ – удельная энтальпия на выходе изэнтропического процесса.

Изэнтропические устройства в термодинамических циклах

Цикл	Изэнтропический шаг	Описание
Идеальный цикл Ренкина	1→2	Изэнтропическое сжатие в насосе
Идеальный цикл Ренкина	3→4	Изэнтропическое расширение в турбине
Идеальный цикл Карно	2→3	Изэнтропическое расширение
Идеальный цикл Карно	4→1	Изэнтропическое сжатие
Идеальный цикл Отто	1→2	Изэнтропическое сжатие
Идеальный цикл Отто	3→4	Изэнтропическое расширение
Идеальный дизельный цикл	1→2	Изэнтропическое сжатие
Идеальный дизельный цикл	3→4	Изэнтропическое расширение
Идеальный цикл Брайтона	1→2	Изэнтропическое сжатие в компрессоре
Идеальный цикл Брайтона	3→4	Изэнтропическое расширение в турбине
Идеальный парокомпрессионный холодильный цикл	1→2	Изэнтропическое сжатие в компрессоре
Идеальный цикл Ленуара	2→3	Изэнтропическое расширение
Идеальный цикл Зейлигера	1→2	Изэнтропическое сжатие
Идеальный цикл Зейлигера	4→5	Изэнтропическое сжатие

Примечание. Предположения об изэнтропии применимы только к идеальным циклам. Реальные циклы имеют неотъемлемые потери из-за неэффективности компрессоров и турбин, а также второго закона термодинамики. Реальные системы не являются истинно изэнтропическими, но изэнтропическое поведение является адекватным приближением для многих расчетных целей.

Изэнтропический поток

В гидродинамике изэнтропический поток — это поток жидкости , который является одновременно адиабатическим и обратимым. То есть к потоку не добавляется тепло и не происходит никаких преобразований энергии за счет трения или диссипативных эффектов . Для изоэнтропического потока идеального газа можно вывести несколько соотношений, определяющих давление, плотность и температуру вдоль линии тока.

Обратите внимание, что обмен энергией с потоком может происходить при изэнтропическом превращении, но только не в виде теплообмена. Примером такого обмена может быть изоэнтропическое расширение или сжатие, которое влечет за собой работу, совершаемую над потоком или с его помощью.

Для изоэнтропического потока плотность энтропии может варьироваться между различными линиями тока. Если плотность энтропии везде одинакова, то поток называется гоментропическим .

Вывод изэнтропических соотношений

Для закрытой системы общее изменение энергии системы равно сумме проделанной работы и подведенного тепла:

$dU=\delta W+\delta Q.$

Обратимая работа, совершаемая системой при изменении объема, равна

$\delta W=-p\,dV,$

где $p$ это давление , и $V$ это объем . Изменение энтальпии ( $H=U+pV$) определяется

$dH=dU+p\,dV+V\,dp.$

Тогда для процесса, который является одновременно обратимым и адиабатическим (т. е. не происходит теплопередачи), $\delta Q_{\text{rev}}=0$, и так $dS=\delta Q_{\text{rev}}/T=0$ Все обратимые адиабатические процессы изоэнтропичны. Это приводит к двум важным наблюдениям:

$dU=\delta W+\delta Q=-p\,dV+0,$

$dH=\delta W+\delta Q+p\,dV+V\,dp=-p\,dV+0+p\,dV+V\,dp=V\,dp.$

Далее, многое можно вычислить для изоэнтропических процессов идеального газа. Для любого превращения идеального газа всегда верно, что

$dU=nC_{v}\,dT$, и $dH=nC_{p}\,dT.$

Используя общие результаты, полученные выше для $dU$ и $dH$, затем

$dU=nC_{v}\,dT=-p\,dV,$

$dH=nC_{p}\,dT=V\,dp.$

Таким образом, для идеального газа коэффициент теплоемкости можно записать как

$\gamma ={\frac {C_{p}}{C_{V}}}=-{\frac {dp/p}{dV/V}}.$

Для калорически идеального газа $\gamma$ является постоянным. Следовательно, интегрируя приведенное выше уравнение, предполагая, что газ калорически совершенен, мы получаем

$pV^{\gamma }={\text{constant}},$

то есть,

${\frac {p_{2}}{p_{1}}}=\left({\frac {V_{1}}{V_{2}}}\right)^{\gamma }.$

Используя уравнение состояния идеального газа, $pV=nRT$,

$TV^{\gamma -1}={\text{constant}}.$

(Доказательство: $PV^{\gamma }={\text{constant}}\Rightarrow PV\,V^{\gamma -1}={\text{constant}}\Rightarrow nRT\,V^{\gamma -1}={\text{constant}}.$ Но nR = сама константа, поэтому $TV^{\gamma -1}={\text{constant}}$.)

${\frac {p^{\gamma -1}}{T^{\gamma }}}={\text{constant}}$

также для постоянного $C_{p}=C_{v}+R$ (на моль),

${\frac {V}{T}}={\frac {nR}{p}}$ и $p={\frac {nRT}{V}}$

$S_{2}-S_{1}=nC_{p}\ln \left({\frac {T_{2}}{T_{1}}}\right)-nR\ln \left({\frac {p_{2}}{p_{1}}}\right)$

${\frac {S_{2}-S_{1}}{n}}=C_{p}\ln \left({\frac {T_{2}}{T_{1}}}\right)-R\ln \left({\frac {T_{2}V_{1}}{T_{1}V_{2}}}\right)=C_{v}\ln \left({\frac {T_{2}}{T_{1}}}\right)+R\ln \left({\frac {V_{2}}{V_{1}}}\right)$

Таким образом, для изэнтропических процессов с идеальным газом

$T_{2}=T_{1}\left({\frac {V_{1}}{V_{2}}}\right)^{(R/C_{v})}$ или $V_{2}=V_{1}\left({\frac {T_{1}}{T_{2}}}\right)^{(C_{v}/R)}$

Таблица изэнтропических соотношений идеального газа

${\frac {T_{2}}{T_{1}}}$	$=$	$\left({\frac {P_{2}}{P_{1}}}\right)^{\frac {\gamma -1}{\gamma }}$	$=$	$\left({\frac {V_{1}}{V_{2}}}\right)^{(\gamma -1)}$	$=$	$\left({\frac {\rho _{2}}{\rho _{1}}}\right)^{(\gamma -1)}$
$\left({\frac {T_{2}}{T_{1}}}\right)^{\frac {\gamma }{\gamma -1}}$	$=$	${\frac {P_{2}}{P_{1}}}$	$=$	$\left({\frac {V_{1}}{V_{2}}}\right)^{\gamma }$	$=$	$\left({\frac {\rho _{2}}{\rho _{1}}}\right)^{\gamma }$
$\left({\frac {T_{1}}{T_{2}}}\right)^{\frac {1}{\gamma -1}}$	$=$	$\left({\frac {P_{1}}{P_{2}}}\right)^{\frac {1}{\gamma }}$	$=$	${\frac {V_{2}}{V_{1}}}$	$=$	${\frac {\rho _{1}}{\rho _{2}}}$
$\left({\frac {T_{2}}{T_{1}}}\right)^{\frac {1}{\gamma -1}}$	$=$	$\left({\frac {P_{2}}{P_{1}}}\right)^{\frac {1}{\gamma }}$	$=$	${\frac {V_{1}}{V_{2}}}$	$=$	${\frac {\rho _{2}}{\rho _{1}}}$

Получено из

$PV^{\gamma }={\text{constant}},$

$PV=mR_{s}T,$

$P=\rho R_{s}T,$

где:

$P$ = давление,

$V$ = объем,

$\gamma$ = соотношение удельных теплоемкостей = $C_{p}/C_{v}$,

$T$ = температура,

$m$ = масса,

$R_{s}$ = газовая константа для конкретного газа = $R/M$,

$R$ = универсальная газовая постоянная,

$M$ = молекулярная масса конкретного газа,

$\rho$ = плотность,

$C_{p}$ = удельная теплоемкость при постоянном давлении,

$C_{v}$ = удельная теплоемкость при постоянном объеме.

См. также

• Газовые законы
• Адиабатический процесс
• Изентальпический процесс
• Изэнтропический анализ
• Политропный процесс

Ссылки

• Ван Вайлен, Дж. Дж. и Зоннтаг, Р. Э. (1965), Основы классической термодинамики , John Wiley & Sons, Inc., Нью-Йорк. Номер карточки каталога Библиотеки Конгресса: 65-19470