Второй закон термодинамики

Второй закон термодинамики — это физический закон, основанный на универсальных эмпирических наблюдениях, касающихся тепла и взаимопреобразований энергии . Простая формулировка закона заключается в том, что тепло всегда самопроизвольно течет от более горячих областей материи к более холодным (или «вниз» с точки зрения температурного градиента). Другое утверждение звучит так: «Не все тепло можно превратить в работу в циклическом процессе ».

Второй закон термодинамики устанавливает понятие энтропии как физического свойства термодинамической системы . Он предсказывает, запрещены ли процессы, несмотря на соблюдение требования сохранения энергии , выраженного в первом законе термодинамики , и обеспечивает необходимые критерии для спонтанных процессов . Например, первый закон допускает процесс падения чашки со стола и разбивания об пол, а также обратный процесс, когда фрагменты чашки собираются вместе и «прыгают» обратно на стол, а второй закон допускает первое и отрицает второе. Второй закон можно сформулировать, исходя из наблюдения, что энтропия изолированных систем, предоставленных для спонтанной эволюции, не может уменьшаться, поскольку они всегда стремятся к состоянию термодинамического равновесия , где энтропия максимальна при данной внутренней энергии. Увеличение совокупной энтропии системы и окружающей среды объясняет необратимость природных процессов, часто упоминаемую в концепции стрелы времени .

Исторически второй закон был эмпирическим открытием , которое было принято как аксиома термодинамической теории . Статистическая механика дает микроскопическое объяснение закона с точки зрения распределения вероятностей состояний больших ансамблей атомов или молекул . Второй закон выражался по-разному. Первой ее формулировкой, предшествовавшей правильному определению энтропии и основанной на теории теплорода , является теорема Карно , сформулированная французским учёным Сади Карно , который в 1824 году показал, что эффективность преобразования тепла в работу в тепловой машине имеет верхний предел. предел. Первое строгое определение второго закона, основанное на понятии энтропии, было дано немецким ученым Рудольфом Клаузиусом в 1850-х годах и включало его утверждение, что тепло никогда не может перейти от более холодного тела к более теплому без какого-либо другого, связанного с этим изменения, происходящего при в то же время.

Второй закон термодинамики позволяет определить понятие термодинамической температуры , но формально это было делегировано нулевому закону термодинамики .

Введение

Передача тепла от горячей воды к холодной воде

Первый закон термодинамики дает определение внутренней энергии и термодинамической системы выражает ее изменение для замкнутой системы через работу и теплоту . Это можно связать с законом сохранения энергии . Концептуально первый закон описывает фундаментальный принцип, согласно которому системы не потребляют и не «расходуют» энергию, что энергия не создается и не уничтожается, а просто преобразуется из одной формы в другую.

Второй закон касается направления естественных процессов. Он утверждает, что естественный процесс протекает только в одном смысле и необратим. То есть состояние самой природной системы можно обратить вспять, но не без увеличения энтропии окружения системы, то есть и состояние системы, и состояние ее окружения не могут быть вместе, полностью обращены, не подразумевая при этом разрушение энтропии.

Например, когда путь для проводимости или излучения имеется , тепло всегда самопроизвольно перетекает от более горячего тела к более холодному. Такие явления объясняются изменением энтропии . Тепловой насос может обратить этот тепловой поток вспять, но и обратный процесс, и исходный процесс вызывают производство энтропии, тем самым увеличивая энтропию окружающей среды системы. Если изолированная система, содержащая отдельные подсистемы, изначально удерживается во внутреннем термодинамическом равновесии за счет внутреннего разделения непроницаемыми стенками между подсистемами, а затем какая-то операция делает стенки более проницаемыми, то система самопроизвольно развивается, чтобы достичь окончательного нового внутреннего термодинамического равновесия , и ее полная энтропия, $S$, увеличивается.

В обратимом или квазистатическом идеализированном процессе передачи энергии в виде тепла в интересующую замкнутую термодинамическую систему (которая допускает вход или выход энергии, но не передачу материи) из вспомогательной термодинамической системы бесконечно малое приращение ( $\mathrm {d} S$) в энтропии интересующей системы определяется как результат бесконечно малой передачи тепла ( $\delta Q$) к интересующей системе, разделенной на общую термодинамическую температуру $(T)$ интересующей системы и вспомогательной термодинамической системы:

$\mathrm {d} S={\frac {\delta Q}{T}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{(closed system; idealized, reversible process)}}.$

используются разные обозначения. Для бесконечно малого количества тепла $(\delta )$ и бесконечно малое изменение энтропии $(\mathrm {d} )$ потому что энтропия является функцией состояния , а тепло, как и работа, нет.

Для реально возможного бесконечно малого процесса без обмена массой с окружающей средой второй закон требует, чтобы приращение энтропии системы удовлетворяло неравенству

$\mathrm {d} S>{\frac {\delta Q}{T_{\text{surr}}}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{(closed system; actually possible, irreversible process).}}$

Это связано с тем, что общий процесс для этого случая (отсутствие массообмена между системой и ее окружением) может включать работу, совершаемую над системой ее окружением, которая может иметь фрикционные или вязкие эффекты внутри системы, поскольку химическая реакция может происходить в прогресс, или потому, что теплообмен на самом деле происходит только необратимо, обусловленный конечной разницей между температурой системы ( T ) и температурой окружающей среды ( T _surr ).

Равенство по-прежнему справедливо для чистого теплового потока (только тепловой поток, без изменений химического состава и массы),

$\mathrm {d} S={\frac {\delta Q}{T}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{(actually possible quasistatic irreversible process without composition change).}}$

что является основой точного определения абсолютной энтропии чистых веществ по измеренным кривым теплоемкости и изменениям энтропии при фазовых переходах, т. е. методом калориметрии.

Представляем набор внутренних переменных $\xi$ для описания отклонения термодинамической системы от состояния химического равновесия в физическом равновесии (с необходимыми вполне определенными однородным давлением Р и температурой Т ) можно записать равенство

$\mathrm {d} S={\frac {\delta Q}{T}}-{\frac {1}{T}}\sum _{j}\,\Xi _{j}\,\delta \xi _{j}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{(closed system; actually possible quasistatic irreversible process).}}$

Второй член представляет собой работу внутренних переменных, которая может быть нарушена внешними воздействиями, но система не может совершать какую-либо положительную работу через внутренние переменные. Это утверждение вводит невозможность обращения эволюции термодинамической системы во времени и может рассматриваться как формулировка второго принципа термодинамики – формулировка, которая, конечно, эквивалентна формулировке принципа в терминах энтропии. .

Нулевой закон термодинамики в своей обычной краткой формулировке позволяет признать, что два тела, находящиеся в состоянии теплового равновесия, имеют одинаковую температуру, особенно то, что пробное тело имеет ту же температуру, что и эталонное термометрическое тело. Для тела, находящегося в тепловом равновесии с другим, существует неопределенно много эмпирических температурных шкал, обычно соответственно зависящих от свойств конкретного эталонного термометрического тела. Второй закон позволяет выделенная температурная шкала, которая определяет абсолютную термодинамическую температуру , независимую от свойств какого-либо конкретного эталонного термометрического тела.

Различные положения закона

Второй закон термодинамики можно выразить многими конкретными способами: наиболее выдающиеся классические высказывания Это утверждение Рудольфа Клаузиуса (1854 г.), утверждение лорда Кельвина (1851 г.) и утверждение в области аксиоматической термодинамики Константина Каратеодори (1909 г.). Эти утверждения формулируют закон в общих физических терминах, ссылаясь на невозможность определенных процессов. Было показано, что утверждения Клаузиуса и Кельвина эквивалентны.

Принцип Карно

Историческое происхождение Второй закон термодинамики был сформулирован в Сади Карно теоретическом анализе потока тепла в паровых машинах (1824 г.). Центральным элементом этого анализа, теперь известного как двигатель Карно , является идеальная тепловая машина, фиктивно работающая в предельном режиме крайней медленности, известном как квазистатический, так что передача тепла и работы происходит между подсистемами, которые всегда находятся в своих собственных внутренних системах. состояния термодинамического равновесия . Он представляет собой теоретический максимальный КПД теплового двигателя, работающего между любыми двумя заданными тепловыми или тепловыми резервуарами при разных температурах. Принцип Карно был признан Карно в то время, когда теория теплорода представляла собой доминирующее понимание природы тепла, до признания первого закона термодинамики и до математического выражения понятия энтропии. Интерпретированный в свете первого закона, анализ Карно физически эквивалентен второму закону термодинамики и остается актуальным и сегодня. Некоторые образцы из его книги:

... везде, где существует разница температур, может быть создана движущая сила.

Производство движущей силы в паровых машинах происходит тогда не за счет фактического потребления теплоты, а за счет ее транспортировки от теплого тела к холодному телу...

Движущая сила тепла не зависит от агентов, используемых для ее реализации; количество его определяется исключительно температурами тел, между которыми осуществляется, наконец, перенос теплоты.

Говоря современным языком, принцип Карно можно сформулировать более точно:

КПД квазистатического или обратимого цикла Карно зависит только от температур двух тепловых резервуаров и одинаков, независимо от рабочего вещества. Двигатель Карно, работающий таким образом, является наиболее эффективной тепловой машиной, использующей эти две температуры.

Более закрытое заявление

Немецкий учёный Рудольф Клаузиус заложил основу второго закона термодинамики в 1850 году, исследовав связь между теплопередачей и работой. Его формулировка второго закона, опубликованная на немецком языке в 1854 году, известна как утверждение Клаузиуса :

Тепло никогда не может перейти от более холодного тела к более теплому без какого-либо другого связанного с этим изменения, происходящего в то же время.

В заявлении Клаузиуса используется концепция «прохождения тепла». Как обычно в термодинамических дискуссиях, это означает «чистую передачу энергии в виде тепла» и не относится к сопутствующим передачам в ту или иную сторону.

Тепло не может самопроизвольно перетекать из холодных областей в горячие без совершения системой внешней работы, что очевидно из обычного опыта охлаждения , например, . В холодильнике тепло передается от холодного к горячему, но только под воздействием внешнего агента — системы охлаждения.

Заявления Кельвина

Лорд Кельвин сформулировал второй закон в нескольких формулировках.

Самодействующая машина не может без посторонней помощи передавать тепло от одного тела к другому при более высокой температуре.

Невозможно с помощью неодушевленных материальных средств получить механический эффект от какой-либо части материи, охладив ее ниже температуры самого холодного из окружающих предметов.

Эквивалентность утверждений Клаузиуса и Кельвина.

Выведите утверждение Кельвина из утверждения Клаузиуса

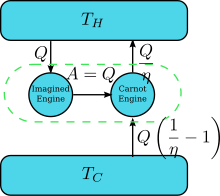
Предположим, что существует двигатель, нарушающий утверждение Кельвина: то есть двигатель, который отбирает тепло и полностью преобразует его в работу (отведенное тепло полностью преобразуется в работу) циклическим образом без какого-либо другого результата. Теперь соедините его с перевернутым двигателем Карно , как показано на рисунке справа. КПД η нормальной тепловой машины равен , поэтому КПД обращенной тепловой машины равен 1/ η . Конечным и единственным эффектом объединенной пары двигателей является передача тепла. ${\textstyle \Delta Q=Q\left({\frac {1}{\eta }}-1\right)}$ из более холодного резервуара в более горячий, что противоречит утверждению Клаузиуса. Это следствие первого закона термодинамики , согласно которому общая энергия системы остается неизменной; ${\textstyle {\text{Input}}+{\text{Output}}=0\implies (Q+Q_{c})-{\frac {Q}{\eta }}=0}$, поэтому поэтому ${\textstyle Q_{c}=Q\left({\frac {1}{\eta }}-1\right)}$, где (1) использовано соглашение о знаках теплоты, при котором теплота, поступающая в двигатель (выходящая из него), является положительной (отрицательной) и (2) ${\frac {Q}{\eta }}$ получается путем определения КПД двигателя при нереверсивном режиме работы двигателя. Таким образом, нарушение утверждения Кельвина подразумевает нарушение утверждения Клаузиуса, т.е. утверждение Клаузиуса подразумевает утверждение Кельвина. Аналогичным образом мы можем доказать, что из утверждения Кельвина следует утверждение Клаузиуса, и, следовательно, они эквивалентны.

Предложение Планка

Планк выдвинул следующее положение, полученное непосредственно из опыта. Иногда это считают его формулировкой второго закона, но он считал ее отправной точкой для вывода второго закона.

Невозможно построить двигатель, который будет работать по полному циклу и не давать никакого эффекта, кроме производства работы и охлаждения теплового резервуара.

Связь между утверждением Кельвина и предложением Планка

В учебниках почти принято говорить о «формулировке закона Кельвина-Планка», как, например, в тексте Тер Хаара и Вергеланда . Эта версия , также известная как утверждение о тепловой машине второго закона , гласит, что

Невозможно создать циклически работающее устройство, единственным эффектом которого было бы поглощение энергии в виде тепла из одного теплового резервуара и выполнение эквивалентного количества работы .

Заявление Планка

Планк сформулировал второй закон следующим образом.

Всякий процесс, происходящий в природе, протекает в том смысле, что сумма энтропий всех тел, участвующих в этом процессе, увеличивается. В пределе, т. е. для обратимых процессов, сумма энтропий остается неизменной.

Утверждение Планка относительно необратимых явлений весьма похоже на утверждение Уленбека и Форда .

... при необратимом или самопроизвольном переходе от одного состояния равновесия к другому (как, например, при выравнивании температуры двух тел А и В при контакте) энтропия всегда возрастает.

Принцип Каратеодори

Константин Каратеодори сформулировал термодинамику на чисто математической аксиоматической основе. Его формулировка второго закона известна как Принцип Каратеодори, который можно сформулировать следующим образом:

В каждой окрестности любого состояния S адиабатически замкнутой системы существуют состояния, недоступные из S.

описал концепцию адиабатической доступности В этой формулировке он впервые и заложил основу для нового раздела классической термодинамики, часто называемого геометрической термодинамикой . Из принципа Каратеодори следует, что количество энергии, квазистатически передаваемой в виде тепла, является функцией голономного процесса , другими словами, $\delta Q=TdS$.

Хотя в учебниках почти принято говорить, что принцип Каратеодори выражает второй закон, и рассматривать его как эквивалент утверждений Клаузиуса или Кельвина-Планка, это не так. Чтобы получить все содержание второго закона, принцип Каратеодори необходимо дополнить принципом Планка, согласно которому изохорная работа всегда увеличивает внутреннюю энергию замкнутой системы, которая изначально находилась в собственном внутреннем термодинамическом равновесии.

Принцип Планка

В 1926 году Макс Планк написал важную статью по основам термодинамики. Он указал на принцип

Внутренняя энергия замкнутой системы увеличивается за счет адиабатического процесса, в течение которого объем системы остается постоянным.

В этой формулировке не упоминается тепло, не упоминается температура или даже энтропия, и она не обязательно неявно опирается на эти понятия, но подразумевает содержание второго закона. Тесно связанное с этим утверждение заключается в том, что «давление трения никогда не совершает положительной работы». Планк писал: «Производство тепла за счет трения необратимо».

Не говоря уже об энтропии, этот принцип Планка излагается в физических терминах. Оно очень тесно связано с утверждением Кельвина, приведенным выше. Важно отметить, что для системы при постоянном объеме и мольном числе энтропия является монотонной функцией внутренней энергии. Тем не менее, этот принцип Планка на самом деле не является предпочитаемой Планком формулировкой второго закона, которая цитируется выше, в предыдущем подразделе настоящего раздела настоящей статьи, и опирается на концепцию энтропии.

Утверждение, в некотором смысле дополняющее принцип Планка, сделано Боргнакке и Зоннтаг. Они не предлагают это как полное изложение второго закона:

... есть только один способ уменьшить энтропию [замкнутой] системы - это передача тепла от системы.

В отличие от вышеизложенного принципа Планка, этот принцип явно основан на изменении энтропии. Удаление материи из системы также может уменьшить ее энтропию.

Связь второго закона с определением температуры

Было показано, что второй закон эквивалентен внутренней энергии U, определяемой как выпуклая функция других обширных свойств системы. То есть, когда система описывается путем указания ее внутренней энергии U , обширной переменной, как функции ее энтропии S , объема V и числа молей N , то есть U = U ( S , V , N ), тогда температура равна частной производной внутренней энергии по энтропии (по сути эквивалентно первому уравнению TdS для V и N постоянных ):

$T=\left({\frac {\partial U}{\partial S}}\right)_{V,N}$

Утверждения второго закона, такие как неравенство Клаузиуса, связанные с потоками излучения.

Неравенство Клаузиуса, а также некоторые другие положения второго закона необходимо переформулировать, чтобы они имели общую применимость для всех форм теплопередачи, т.е. для сценариев, включающих радиационные потоки. Например, подынтегральная функция (đQ/T) выражения Клаузиуса применима к теплопроводности и конвекции, а также к случаю передачи идеального бесконечно малого излучения черного тела (BR), но не применима к большинству сценариев передачи излучения и в некоторых случаях не имеет физического значения. смысл какой угодно. Следовательно, неравенство Клаузиуса было переформулировано. так что это применимо к циклам с процессами, включающими любую форму теплопередачи. Перенос энтропии с радиационными потоками ( $\delta S_{\text{NetRad}}$) берется отдельно от теплопередачи за счет теплопроводности и конвекции ( $\delta Q_{CC}$), где температура оценивается на границе системы, где происходит теплообмен. Тогда модифицированное неравенство Клаузиуса для всех сценариев теплопередачи можно выразить как:

$$\int _{\text{cycle}}({\frac {\delta Q_{CC}}{T_{b}}}+\delta S_{\text{NetRad}})<=0$$

Короче говоря, неравенство Клаузиуса гласит, что по завершении цикла изменение свойства состояния S будет равно нулю, поэтому энтропия, произведенная во время цикла, должна быть передана из системы путем теплопередачи. $\delta$ (или đ) указывает на интеграцию, зависящую от пути.

Из-за того, что вся материя излучает излучение, большинство расчетов потоков энтропии включают падающие, отраженные и испускаемые потоки излучения. Энергия и энтропия неполяризованного теплового излучения черного тела рассчитываются с использованием выражений спектральной энергии и энтропии яркости, полученных Максом Планком. используя равновесную статистическую механику,

$$K_{\nu }={\frac {2h}{c^{2}}}{\frac {\nu ^{3}}{\exp \left({\frac {h\nu }{kT}}\right)-1}},$$$$L_{\nu }={\frac {2k\nu ^{2}}{c^{2}}}((1+{\frac {c^{2}K_{\nu }}{2h\nu ^{3}}})\ln(1+{\frac {c^{2}K_{\nu }}{2h\nu ^{3}}})-({\frac {c^{2}K_{\nu }}{2h\nu ^{3}}})\ln({\frac {c^{2}K_{\nu }}{2h\nu ^{3}}}))$$

где c — скорость света или (2,9979)10 ⁸ м/с , k — постоянная Больцмана или (1.38)10 ⁻²³ J/K , h — постоянная Планка или (6,626)10 ^-34  J s, v – частота (с ⁻¹ ), а величины K _v и L _v — потоки энергии и энтропии на единицу частоты, площади и телесного угла. Выводя это спектральное энтропийное излучение черного тела с целью вывода формулы энергии черного тела, Планк постулировал, что энергия фотона квантуется (частично для упрощения математики), тем самым положив начало квантовой теории.

Подход неравновесной статистической механики также использовался для получения того же результата, что и Планк, что указывает на то, что он имеет более широкое значение и представляет собой неравновесную энтропию. График зависимости K _v от частоты (v) для различных значений температуры ( T) дает семейство энергетических спектров излучения черного тела, а также спектров энтропии. Для потоков излучения нечернотельного излучения (NBR) спектральная энтропийная яркость L _v находится путем подстановки K _v данных о спектральной энергетической яркости в выражение L _v (отмечая, что излучаемые и отраженные потоки энтропии, как правило, не являются независимыми). Для излучения NBR, включая излучение серого тела (GR), результирующий излучаемый поток энтропии или яркость L имеет более высокое соотношение энтропии к энергии ( L/K ), чем у BR. То есть поток энтропии эмиссии NBR дальше от результата проводимости и конвекции q / T , чем поток энтропии эмиссии BR. Это наблюдение согласуется с формулами энергии и энтропии излучения черного тела Макса Планка и согласуется с тем фактом, что излучение черного тела представляет собой максимальное излучение энтропии для всех материалов с одинаковой температурой, а также максимальное излучение энтропии для всех излучений с одинаковой температурой. энергетическое сияние.

Обобщенная концептуальная формулировка принципа второго закона

Анализ второго закона ценен в научном и инженерном анализе, поскольку он дает ряд преимуществ по сравнению с одним лишь энергетическим анализом, включая основу для определения качества энергии (эксергетического содержания ), понимание фундаментальных физических явлений, а также улучшение оценки и оптимизации производительности. В результате концептуальная формулировка принципа очень полезна в инженерном анализе. Термодинамические системы можно классифицировать по четырем комбинациям энтропии (S) вверх или вниз и однородности (Y) - между системой и ее средой - вверх или вниз. Эта «особая» категория процессов, категория IV, характеризуется движением в направлении низкого беспорядка и низкой однородности, противодействуя тенденции второго закона к единообразию и беспорядку.

Четыре категории процессов с увеличением или уменьшением энтропии и увеличением или уменьшением однородности.

Второй закон можно концептуально сформулировать следующим образом: Материя и энергия имеют тенденцию достигать состояния однородности или внутреннего и внешнего равновесия, состояния максимального беспорядка (энтропии). Реальные неравновесные процессы всегда производят энтропию, вызывая усиление беспорядка во Вселенной, в то время как идеализированные обратимые процессы не производят энтропии, и неизвестно, что существует какой-либо процесс, разрушающий энтропию. Тенденции системы к единообразию можно противодействовать, и система может стать более упорядоченной или сложной за счет сочетания двух вещей: источника работы или энергии и некоторой формы обучения или интеллекта. Где «эксергия» — это тепловой, механический, электрический или химический рабочий потенциал источника энергии или потока, а «инструкция или интеллект», хотя и субъективны, находятся в контексте набора процессов категории IV.

Рассмотрим пример категории IV: роботизированное производство и сборка автомобилей на заводе. Роботизированное оборудование требует выполнения электрических работ и инструкций, но после завершения произведенная продукция становится менее однородной по отношению к окружающей среде или более сложной (более высокий порядок) по сравнению с сырьем, из которого она была изготовлена. Таким образом, энтропия или беспорядок системы уменьшается, в то время как тенденция к единообразию между системой и ее окружением противодействует. В этом примере инструкции, а также источник работы могут быть внутренними или внешними по отношению к системе, и они могут пересекать или не пересекать границу системы. Например, инструкции могут быть предварительно закодированы, а электротехнические работы могут храниться в системе хранения энергии на месте. Альтернативно, управление оборудованием может осуществляться дистанционно по сети связи, тогда как электроэнергия подается на завод из местной электросети. Кроме того, люди могут полностью или частично напрямую играть ту роль, которую роботизированное оборудование играет в производстве. В этом случае могут иметь место инструкции, но интеллект несет либо прямую, либо косвенную ответственность за направление или применение работы таким образом, чтобы противодействовать тенденции к беспорядку и единообразию.

Бывают также ситуации, когда энтропия самопроизвольно уменьшается за счет переноса энергии и энтропии. Когда термодинамические ограничения отсутствуют, энергия или масса, а также сопутствующая энтропия могут спонтанно передаваться из системы в процессе достижения внешнего равновесия или единообразия интенсивных свойств системы с ее окружением. Это происходит спонтанно, потому что энергия или масса, передаваемая из системы в ее окружение, приводит к повышению энтропии в окружающей среде, то есть к более высокой общей энтропии системы и ее окружения. Обратите внимание, что этот перенос энтропии требует нарушения равновесия в свойствах, таких как разница температур. Одним из примеров этого является охлаждающая кристаллизация воды, которая может произойти, когда температура окружающей среды в системе ниже нуля. Неограниченная теплопередача может происходить самопроизвольно, что приводит к замерзанию молекул воды в кристаллическую структуру пониженного беспорядка (склеивание в определенном порядке из-за молекулярного притяжения). Энтропия системы уменьшается, но система приближается к однородности с окружением (категория III).

С другой стороны, рассмотрим охлаждение воды в теплой среде. Из-за охлаждения, когда тепло извлекается из воды, температура и энтропия воды уменьшаются по мере того, как система все дальше отходит от однородности с теплым окружением или окружающей средой (категория IV). Главный вывод заключается в том, что охлаждение требует не только источника работы, но и специально разработанного оборудования, а также заранее запрограммированного или прямого оперативного анализа или инструкций для достижения желаемого эффекта охлаждения.

Следствия

Вечный двигатель второго рода

Основная статья: Вечный двигатель

До установления второго закона многие люди, заинтересованные в изобретении вечного двигателя, пытались обойти ограничения первого закона термодинамики , извлекая огромную внутреннюю энергию окружающей среды в качестве мощности машины. Такая машина называется «вечным двигателем второго рода». Второй закон заявил о невозможности создания таких машин.

Теорема Карно

Теорема Карно (1824 г.) — это принцип, ограничивающий максимальный КПД любого возможного двигателя. Эффективность зависит исключительно от разницы температур между горячими и холодными термальными резервуарами. Теорема Карно гласит:

• Все необратимые тепловые машины между двумя тепловыми резервуарами менее эффективны, чем двигатель Карно, работающий между теми же резервуарами.
• Все обратимые тепловые двигатели, работающие между двумя тепловыми резервуарами, одинаково эффективны, как и двигатель Карно, работающий между теми же резервуарами.

В его идеальной модели теплота калорий, преобразованная в работу, могла быть восстановлена ​​путем обращения вспять цикла — концепция, впоследствии известная как термодинамическая обратимость . Карно, однако, далее постулировал, что некоторая часть калорий теряется, не превращаясь в механическую работу. Следовательно, ни одна настоящая тепловая машина не могла реализовать обратимость цикла Карно и была признана менее эффективной.

Хотя это было сформулировано в терминах теплородности (см. устаревшую теорию теплорода ), а не энтропии , это было раннее понимание второго закона.

Положение о неравенстве

Теорема Клаузиуса (1854 г.) утверждает, что в циклическом процессе

$\oint {\frac {\delta Q}{T_{\text{surr}}}}\leq 0.$

Равенство имеет место в обратимом случае и строгое неравенство сохраняется в необратимом случае, где T _surr здесь является температурой тепловой ванны (окружающей среды). Обратимый случай используется для введения энтропии функции состояния . Это связано с тем, что в циклических процессах изменение функции состояния равно нулю от функциональности состояния.

Термодинамическая температура

Основная статья: Термодинамическая температура

Для произвольной тепловой машины КПД равен:

$\eta ={\frac {|W_{n}|}{q_{H}}}={\frac {q_{H}+q_{C}}{q_{H}}}=1-{\frac {|q_{C}|}{|q_{H}|}}$ ( 1 )

где W _n — чистая работа, совершаемая двигателем за цикл, q _H > 0 — тепло, передаваемое двигателю из горячего резервуара, а q _C = - | q _С | < 0 — это отходящее тепло, отдаваемое двигателем в холодный резервуар. Таким образом, эффективность зависит только от соотношения | q _С | / | q _Ч |.

Теорема Карно утверждает, что все обратимые двигатели, работающие с одними и теми же тепловыми резервуарами, одинаково эффективны. Таким образом, любая обратимая тепловая машина, работающая в диапазоне температур T _H и T _C, должна иметь одинаковый КПД, то есть КПД является функцией только температур:

${\frac {|q_{C}|}{|q_{H}|}}=f(T_{H},T_{C}).$ ( 2 )

Кроме того, обратимая тепловая машина, работающая между температурами Т ₁ и Т _{3 ,} должна иметь такой же КПД, как и состоящая из двух циклов, один между Т ₁ и другой (промежуточной) температурой Т ₂ , а второй между Т ₂ и Т ₃ , где Т ₁ > Т ₂ > Т ₃ . Это связано с тем, что если часть двухтактного двигателя скрыта так, что она распознается как двигатель между резервуарами при температурах Т ₁ и Т ₃ , то КПД этого двигателя должен быть таким же, как и у другого двигателя при той же температуре. резервуары. Если мы выберем двигатели так, чтобы работа, выполняемая однотактным двигателем и двухтактным двигателем, была одинаковой, то КПД каждой тепловой машины запишется следующим образом.

$\eta _{1}=1-{\frac {|q_{3}|}{|q_{1}|}}=1-f(T_{1},T_{3})$,

$\eta _{2}=1-{\frac {|q_{2}|}{|q_{1}|}}=1-f(T_{1},T_{2})$,

$\eta _{3}=1-{\frac {|q_{3}|}{|q_{2}|}}=1-f(T_{2},T_{3})$.

Здесь двигатель 1 представляет собой однотактный двигатель, а двигатели 2 и 3 образуют двухтактный двигатель с промежуточным резервуаром в точке Т ₂ . Мы также использовали тот факт, что тепло $q_{2}$ проходит через промежуточный тепловой резервуар при $T_{2}$ не теряя своей энергии. (То есть, $q_{2}$ не теряется при прохождении через резервуар при $T_{2}$.) Этот факт можно доказать следующим.

${\begin{aligned}&{{\eta }_{2}}=1-{\frac {|{{q}_{2}}|}{|{{q}_{1}}|}}\to |{{w}_{2}}|=|{{q}_{1}}|-|{{q}_{2}}|,\\&{{\eta }_{3}}=1-{\frac {|{{q}_{3}}|}{|{{q}_{2}}^{*}|}}\to |{{w}_{3}}|=|{{q}_{2}}^{*}|-|{{q}_{3}}|,\\&|{{w}_{2}}|+|{{w}_{3}}|=(|{{q}_{1}}|-|{{q}_{2}}|)+(|{{q}_{2}}^{*}|-|{{q}_{3}}|),\\&{{\eta }_{1}}=1-{\frac {|{{q}_{3}}|}{|{{q}_{1}}|}}={\frac {(|{{w}_{2}}|+|{{w}_{3}}|)}{|{{q}_{1}}|}}={\frac {(|{{q}_{1}}|-|{{q}_{2}}|)+(|{{q}_{2}}^{*}|-|{{q}_{3}}|)}{|{{q}_{1}}|}}.\\\end{aligned}}$

Чтобы добиться согласованности в последнем уравнении, тепло $q_{2}$ перетекающее от двигателя 2 в промежуточный резервуар должно быть равно теплу $q_{2}^{*}$ вытекло из бачка в двигатель 3.

Затем

$f(T_{1},T_{3})={\frac {|q_{3}|}{|q_{1}|}}={\frac {|q_{2}||q_{3}|}{|q_{1}||q_{2}|}}=f(T_{1},T_{2})f(T_{2},T_{3}).$

Теперь рассмотрим случай, когда $T_{1}$ — фиксированная эталонная температура: температура тройной точки воды равна 273,16 Кельвина; $T_{1}=273.16K$. для любых T ₂ и T ₃ Тогда

$f(T_{2},T_{3})={\frac {f(T_{1},T_{3})}{f(T_{1},T_{2})}}={\frac {273.16{\text{ K}}\cdot f(T_{1},T_{3})}{273.16{\text{ K}}\cdot f(T_{1},T_{2})}}.$

Следовательно, если термодинамическая температура Т * определяется выражением

$T^{*}=273.16{\text{ K}}\cdot f(T_{1},T)$

тогда функция f , рассматриваемая как функция термодинамических температур, просто

$f(T_{2},T_{3})=f(T_{2}^{*},T_{3}^{*})={\frac {T_{3}^{*}}{T_{2}^{*}}},$

и эталонная температура T ₁ * = 273,16 К × f ( T ₁ , T ₁ ) = 273,16 К. (Можно использовать любую эталонную температуру и любое положительное числовое значение – выбор здесь соответствует шкале Кельвина .)

Энтропия

Основная статья: Энтропия (классическая термодинамика)

Согласно равенству Клаузиуса , для обратимого процесса

$\oint {\frac {\delta Q}{T}}=0$

Это означает, что линейный интеграл $\int _{L}{\frac {\delta Q}{T}}$ не зависит от пути для обратимых процессов.

Таким образом, мы можем определить функцию состояния S, называемую энтропией, которая для обратимого процесса или чистой теплопередачи удовлетворяет условию

$dS={\frac {\delta Q}{T}}$

При этом мы можем получить разницу энтропии только путем интегрирования приведенной выше формулы. Чтобы получить абсолютное значение, нам нужен третий закон термодинамики , который гласит, что S = 0 при абсолютном нуле для идеальных кристаллов.

Для любого необратимого процесса, поскольку энтропия является функцией состояния, мы всегда можем связать начальное и конечное состояния с воображаемым обратимым процессом и интегрировать по этому пути, чтобы вычислить разницу в энтропии.

Теперь обратим обратимый процесс и объединим его с указанным необратимым процессом. Применяя неравенство Клаузиуса к этому контуру, где T _surr представляет собой температуру окружающей среды,

$-\Delta S+\int {\frac {\delta Q}{T_{surr}}}=\oint {\frac {\delta Q}{T_{surr}}}\leq 0$

Таким образом,

$\Delta S\geq \int {\frac {\delta Q}{T_{surr}}}$

где равенство имеет место, если преобразование обратимо. Если процесс является адиабатическим , то $\delta Q=0$, так $\Delta S\geq 0$.

Энергия, наличие полезной работы

См. Также: Эксергия

Важным и показательным идеализированным частным случаем является рассмотрение применения второго закона к сценарию изолированной системы (называемой полной системой или вселенной), состоящей из двух частей: интересующей подсистемы и окружения подсистемы. Предполагается, что эта среда настолько велика, что ее можно рассматривать как неограниченный резервуар тепла при температуре T _R и давлении P _R – так что независимо от того, сколько тепла передается в подсистему (или из нее), температура останется TR _; окружение и сколько бы объем подсистемы ни расширялся (или сжимался), давление окружающей среды останется P _R .

Какие бы изменения dS и dS _R ни происходили в энтропии подсистемы и среды в отдельности, энтропия S _tot изолированной целостной системы не должна уменьшаться согласно второму началу термодинамики:

$dS_{\mathrm {tot} }=dS+dS_{R}\geq 0$

Согласно первому закону термодинамики , изменение dU внутренней энергии подсистемы представляет собой сумму тепла δq, добавленного к подсистеме, минус любая работа δw, совершенная подсистемой , плюс любая чистая химическая энергия. входя в подсистему d Σ µ _iR N _i , так что:

$dU=\delta q-\delta w+d\left(\sum \mu _{iR}N_{i}\right)$

где μ _iR – химические потенциалы химических частиц во внешней среде.

Теперь тепло, покидающее резервуар и попадающее в подсистему, равно

$\delta q=T_{R}(-dS_{R})\leq T_{R}dS$

где мы впервые использовали определение энтропии в классической термодинамике (альтернативно в статистической термодинамике можно вывести связь между изменением энтропии, температурой и поглощенным теплом); а затем неравенство Второго закона сверху.

Отсюда следует, что любая чистая работа δw, выполняемая подсистемой, должна подчиняться

$\delta w\leq -dU+T_{R}dS+\sum \mu _{iR}dN_{i}$

Полезно разделить работу δw, выполняемую подсистемой, на полезную работу δw _u , которую может выполнить подсистема , помимо работы p _R dV, совершаемой просто подсистемой, расширяющейся против окружающего внешнего давления: давая следующее соотношение для полезной работы (эксергии), которую можно совершить:

$\delta w_{u}\leq -d\left(U-T_{R}S+p_{R}V-\sum \mu _{iR}N_{i}\right)$

Правую часть удобно определить как точную производную термодинамического потенциала, называемого доступностью или эксергией E подсистемы:

$E=U-T_{R}S+p_{R}V-\sum \mu _{iR}N_{i}$

Таким образом, Второй закон подразумевает, что для любого процесса, который можно рассматривать как просто разделенный на подсистему и неограниченный резервуар температуры и давления, с которым он находится в контакте,

$dE+\delta w_{u}\leq 0$

т.е. изменение эксергии подсистемы плюс полезная работа, совершаемая подсистемой (или изменение эксергии подсистемы за вычетом любой работы, дополнительной к той, которую совершает резервуар под давлением, совершаемой в системе) должно быть меньше или равно нулю. .

В целом, если в качестве окружения системы в реальном мире выбрано правильное эталонное состояние , подобное бесконечному резервуару , то второй закон предсказывает уменьшение E для необратимого процесса и отсутствие изменений для обратимого процесса.

$dS_{tot}\geq 0$ эквивалентно $dE+\delta w_{u}\leq 0$

Это выражение вместе с соответствующим эталонным состоянием позволяет инженеру-конструктору, работающему в макроскопическом масштабе (выше термодинамического предела ), использовать второй закон без прямого измерения или учета изменения энтропии в полностью изолированной системе. ( Также см. инженер-технолог ). Эти изменения уже рассматривались в предположении, что рассматриваемая система может достичь равновесия с эталонным состоянием без изменения эталонного состояния. Также можно найти эффективность процесса или совокупности процессов, которая сравнивает его с обратимым идеалом ( см. Второй закон эффективности ).

Такой подход ко второму закону широко используется в инженерной практике, экологическом учете , системной экологии и других дисциплинах.

Направление спонтанных процессов

Второй закон определяет, запрещен ли предлагаемый физический или химический процесс или он может произойти спонтанно. Для изолированных систем окружающая среда не обеспечивает энергию, и второй закон требует, чтобы энтропия самой системы увеличивалась: Δ S > 0. Примеры спонтанных физических процессов в изолированных системах включают следующее:

• 1) Тепло может передаваться из области с более высокой температурой в область с более низкой температурой (но не наоборот).
• 2) Механическую энергию можно преобразовать в тепловую (но не наоборот).
• 3) Растворенное вещество может перемещаться из области с большей концентрацией в область с меньшей концентрацией (но не наоборот).

Однако для некоторых неизолированных систем, которые могут обмениваться энергией с окружающей средой, окружающая среда обменивается с системой достаточным количеством тепла или совершает над системой достаточную работу, так что процессы происходят в противоположном направлении. возможно при условии, что общее изменение энтропии системы и окружения положительно, как того требует второй закон: Δ S _tot = Δ S + Δ SR _Это > 0. Для трех приведенных выше примеров:

• 1) Тепло может передаваться из области с более низкой температурой в область с более высокой температурой в холодильнике или в тепловом насосе . Эти машины должны обеспечивать достаточную работу системы.
• 2) Тепловая энергия может быть преобразована в механическую работу в тепловой машине , если также выделяется достаточное количество тепла в окружающую среду.
• 3) Растворенное вещество может перемещаться из области с более низкой концентрацией в область с более высокой концентрацией в биохимическом процессе активного транспорта , если достаточную работу обеспечивает градиент концентрации химического вещества, такого как АТФ , или электрохимический градиент .

Второй закон химической термодинамики.

Для самопроизвольного химического процесса в закрытой системе при постоянной температуре и давлении без не- PV работы неравенство Клаузиуса Δ S > Q/T _surr превращается в условие изменения свободной энергии Гиббса

$\Delta G<0$

или d G < 0. Для аналогичного процесса при постоянной температуре и объеме изменение свободной энергии Гельмгольца должно быть отрицательным, $\Delta A<0$. Таким образом, отрицательное значение изменения свободной энергии ( G или A ) является необходимым условием самопроизвольности процесса. Это наиболее полезная форма второго закона термодинамики в химии, где изменения свободной энергии можно рассчитать на основе табличных энтальпий образования и стандартных молярных энтропий реагентов и продуктов. Условие химического равновесия при постоянных Т и р без учета электрической работы равно d G = 0.

История

Смотрите также: История энтропии

Николя Леонар Сади Карно в традиционной форме студента Политехнической школы.

Первая теория преобразования тепла в механическую работу принадлежит Николя Леонару Сади Карно в 1824 году. Он был первым, кто правильно понял, что эффективность этого преобразования зависит от разницы температур между двигателем и окружающей средой.

Признавая важность работы Джеймса Прескотта Джоуля по сохранению энергии, Рудольф Клаузиус первым сформулировал второй закон в 1850 году в такой форме: тепло не переходит самопроизвольно от холодных тел к горячим. Хотя сейчас это общеизвестно, это противоречило популярной в то время калорической теории тепла, которая рассматривала тепло как жидкость. Отсюда он смог вывести принцип Сади Карно и определение энтропии (1865 г.).

Основанный в XIX веке второй закон Кельвина-Планка не может гласит: «Ни одно устройство, работающее по циклическому принципу, получать тепло из одного резервуара и производить чистый объем работы». Было показано, что это эквивалентно утверждению Клаузиуса.

также Эргодическая гипотеза важна для подхода Больцмана . Оно гласит, что в течение длительных периодов времени время пребывания в некоторой области фазового пространства микросостояний с одинаковой энергией пропорционально объёму этой области, т.е. что все доступные микросостояния равновероятны в течение длительного периода времени. То же самое означает, что среднее по времени и среднее по статистическому ансамблю одинаковы.

Существует традиционная доктрина, начиная с Клаузиуса, согласно которой энтропию можно понимать как молекулярный «беспорядок» внутри макроскопической системы . Эта доктрина устарела.

Отчет Клаузиуса

Рудольф Клаузиус

В 1865 году немецкий физик Рудольф Клаузиус сформулировал то, что он назвал «второй фундаментальной теоремой механической теории тепла » в следующей форме:

$\int {\frac {\delta Q}{T}}=-N$

где Q — тепло, T — температура, а N — «значение эквивалентности» всех некомпенсированных преобразований, участвующих в циклическом процессе. Позже, в 1865 году, Клаузиус определил «эквивалентную ценность» как энтропию. Вслед за этим определением в том же году самая известная версия второго закона была зачитана на презентации в Философском обществе Цюриха 24 апреля, в которой в конце своего выступления Клаузиус заключает:

Энтропия Вселенной стремится к максимуму.

Это утверждение является самой известной формулировкой второго закона. Из-за небрежности его языка, например, Вселенной , а также отсутствия конкретных условий, например, открытости, закрытости или изолированности, многие люди воспринимают это простое утверждение как означающее, что второй закон термодинамики применим практически к любому вообразимому предмету. Это неправда; это утверждение является лишь упрощенной версией более расширенного и точного описания.

С точки зрения изменения во времени математическая формулировка второго закона для изолированной системы, претерпевающей произвольное преобразование, такова:

${\frac {dS}{dt}}\geq 0$

где

S - энтропия системы и

т это время .

Знак равенства применяется после уравновешивания. Альтернативный способ формулировки второго закона для изолированных систем:

${\frac {dS}{dt}}={\dot {S}}_{i}$ с ${\dot {S}}_{i}\geq 0$

с ${\dot {S}}_{i}$ сумма скорости производства энтропии всеми процессами внутри системы. Преимущество этой формулировки в том, что она показывает эффект производства энтропии. Скорость производства энтропии — очень важное понятие, поскольку она определяет (ограничивает) эффективность тепловых машин. Умножается на температуру окружающей среды $T_{a}$ это дает так называемую диссипируемую энергию $P_{diss}=T_{a}{\dot {S}}_{i}$.

Выражение второго закона для закрытых систем (то есть допускающих теплообмен и перемещение границ, но не обмена веществом) таково:

${\frac {dS}{dt}}={\frac {\dot {Q}}{T}}+{\dot {S}}_{i}$ с ${\dot {S}}_{i}\geq 0$

Здесь

${\dot {Q}}$ это тепловой поток в систему

$T$ – температура в точке поступления тепла в систему.

Знак равенства сохраняется в том случае, если внутри системы протекают только обратимые процессы. Если имеют место необратимые процессы (что имеет место в реальных действующих системах), знак > сохраняется. Если тепло подводится к системе в нескольких местах, то необходимо взять алгебраическую сумму соответствующих слагаемых.

Для открытых систем (также допускающих обмен материей):

${\frac {dS}{dt}}={\frac {\dot {Q}}{T}}+{\dot {S}}+{\dot {S}}_{i}$ с ${\dot {S}}_{i}\geq 0$

Здесь ${\dot {S}}$ — поток энтропии в систему, связанный с потоком вещества, поступающего в систему. Его не следует путать с производной энтропии по времени. Если материя поступает в несколько мест, нам придется взять алгебраическую сумму этих вкладов.

Статистическая механика

Статистическая механика дает объяснение второму закону, постулируя, что материал состоит из атомов и молекул, находящихся в постоянном движении. Определенный набор положений и скоростей для каждой частицы в системе называется микросостоянием системы , и из-за постоянного движения система постоянно меняет свое микросостояние. Статистическая механика постулирует, что в равновесии каждое микросостояние, в котором может находиться система, имеет одинаковую вероятность, и когда делается это предположение, это приводит непосредственно к выводу, что второй закон должен выполняться в статистическом смысле. То есть второй закон будет выполняться в среднем со статистическим отклонением порядка 1/ √ N, где N — число частиц в системе. Для повседневных (макроскопических) ситуаций вероятность нарушения второго закона практически равна нулю. Однако для систем с небольшим числом частиц термодинамические параметры, включая энтропию, могут демонстрировать значительные статистические отклонения от предсказываемых вторым законом. Классическая термодинамическая теория не рассматривает эти статистические вариации.

Вывод из статистической механики

Дополнительная информация: H-теорема.

Первый механический аргумент кинетической теории газов о том, что молекулярные столкновения влекут за собой выравнивание температур и, следовательно, тенденцию к равновесию, был выдвинут Джеймсом Клерком Максвеллом в 1860 году; Людвиг Больцман со своей H-теоремой 1872 года также утверждал, что из-за столкновений газы должны со временем стремиться к распределению Максвелла-Больцмана .

Из-за парадокса Лошмидта при выводе Второго закона необходимо сделать предположение относительно прошлого, а именно, что система некоррелирована в какой-то момент в прошлом; это позволяет провести простое вероятностное лечение. Это предположение обычно рассматривается как граничное условие , и, таким образом, второй Закон в конечном итоге является следствием начальных условий где-то в прошлом, вероятно, в начале Вселенной ( Большой взрыв ), хотя другие сценарии . были предложены и

Учитывая эти предположения, в статистической механике Второй закон не является постулатом, а скорее следствием фундаментального постулата , также известного как постулат равной априорной вероятности, при условии, что ясно, что простые вероятностные аргументы применяются только к будущем, тогда как о прошлом существуют вспомогательные источники информации, которые говорят нам, что оно было с низкой энтропией. Первая часть второго закона, который утверждает, что энтропия термически изолированной системы может только возрастать, является тривиальным следствием постулата о равной априорной вероятности, если мы ограничим понятие энтропии системами, находящимися в тепловом равновесии. Энтропия изолированной системы, находящейся в тепловом равновесии, содержащей количество энергии $E$ является:

$S=k_{\mathrm {B} }\ln \left[\Omega \left(E\right)\right]$

где $\Omega \left(E\right)$ — число квантовых состояний в небольшом интервале между $E$ и $E+\delta E$. Здесь $\delta E$ представляет собой макроскопически малый энергетический интервал, который остается фиксированным. Строго говоря, это означает, что энтропия зависит от выбора $\delta E$. Однако в термодинамическом пределе (т. е. в пределе бесконечно большого размера системы) удельная энтропия (энтропия единицы объема или массы) не зависит от $\delta E$.

Предположим, у нас есть изолированная система, макроскопическое состояние которой определяется рядом переменных. Эти макроскопические переменные могут, например, относиться к общему объему, положениям поршней в системе и т. д. Тогда $\Omega$ будет зависеть от значений этих переменных. Если переменная не фиксирована (например, мы не зажимаем поршень в определенном положении), то, поскольку все доступные состояния одинаково вероятны в равновесии, свободная переменная в равновесии будет такой, что $\Omega$ максимизируется при заданной энергии изолированной системы поскольку это наиболее вероятная ситуация в равновесии.

Если изначально переменная была зафиксирована на каком-то значении, то после ее освобождения и достижения нового равновесия, переменная отрегулируется так, что $\Omega$ максимизируется, подразумевает, что энтропия увеличится или останется прежней (если значение, на котором была зафиксирована переменная, оказалось равновесным значением).Предположим, мы начинаем с ситуации равновесия и внезапно снимаем ограничение на переменную. Затем сразу после того, как мы это сделаем, есть ряд $\Omega$ доступных микросостояний, но равновесие еще не достигнуто, поэтому действительные вероятности нахождения системы в некотором доступном состоянии еще не равны априорной вероятности $1/\Omega$. Мы уже видели, что в конечном состоянии равновесия энтропия увеличится или останется такой же по сравнению с предыдущим состоянием равновесия. Больцмана H-теорема , однако, доказывает, что величина H монотонно увеличивается в зависимости от времени во время промежуточного состояния, находящегося вне равновесия.

Вывод изменения энтропии для обратимых процессов.

Вторая часть Второго закона гласит, что изменение энтропии системы, претерпевающей обратимый процесс, определяется выражением:

$dS={\frac {\delta Q}{T}}$

где температура определяется как:

${\frac {1}{k_{\mathrm {B} }T}}\equiv \beta \equiv {\frac {d\ln \left[\Omega \left(E\right)\right]}{dE}}$

См . здесь обоснование этого определения. Предположим, что в системе есть некоторый внешний параметр x , который можно изменить. В общем случае собственные энергетические состояния системы будут зависеть от x . Согласно адиабатической теореме квантовой механики, в пределе бесконечно медленного изменения гамильтониана системы система останется в том же собственном энергетическом состоянии и, таким образом, изменит свою энергию в соответствии с изменением энергии собственного энергетического состояния, в котором она находится.

Обобщенная сила X , соответствующая внешней переменной x, определяется так, что $Xdx$ — работа, выполняемая системой, если x увеличить на величину dx . Например, если x — объем, то X — давление. Обобщенная сила для системы, находящейся в собственном энергетическом состоянии. $E_{r}$ дается:

$X=-{\frac {dE_{r}}{dx}}$

Поскольку система может находиться в любом собственном энергетическом состоянии в интервале $\delta E$, мы определяем обобщенную силу для системы как математическое ожидание приведенного выше выражения:

$X=-\left\langle {\frac {dE_{r}}{dx}}\right\rangle \,$

Чтобы оценить среднее значение, мы разделяем $\Omega \left(E\right)$ собственные состояния энергии, подсчитав, сколько из них имеют значение для ${\frac {dE_{r}}{dx}}$ в диапазоне между $Y$ и $Y+\delta Y$. Звонок на этот номер $\Omega _{Y}\left(E\right)$, у нас есть:

$\Omega \left(E\right)=\sum _{Y}\Omega _{Y}\left(E\right)\,$

Теперь можно записать среднее значение, определяющее обобщенную силу:

$X=-{\frac {1}{\Omega \left(E\right)}}\sum _{Y}Y\Omega _{Y}\left(E\right)\,$

Мы можем связать это с производной энтропии по x при постоянной энергии E следующим образом. Предположим, мы меняем x на x + dx . Затем $\Omega \left(E\right)$ изменится, потому что собственные состояния энергии зависят от x , в результате чего собственные состояния энергии перемещаются в диапазон между $E$ и $E+\delta E$. Давайте снова сосредоточимся на собственных энергетических состояниях, для которых ${\textstyle {\frac {dE_{r}}{dx}}}$ лежит в пределах между $Y$ и $Y+\delta Y$. Поскольку энергия этих собственных состояний энергии увеличивается на Y dx , все такие собственные состояния энергии, находящиеся в интервале от E – Y dx до E, перемещаются снизу E вверх E . Есть

$N_{Y}\left(E\right)={\frac {\Omega _{Y}\left(E\right)}{\delta E}}Ydx\,$

такие собственные энергетические состояния. Если $Ydx\leq \delta E$, все эти собственные состояния энергии переместятся в диапазон между $E$ и $E+\delta E$ и способствовать увеличению $\Omega$. Число собственных состояний энергии, движущихся снизу $E+\delta E$ выше $E+\delta E$ дается $N_{Y}\left(E+\delta E\right)$. Разница

$N_{Y}\left(E\right)-N_{Y}\left(E+\delta E\right)\,$

Таким образом, это чистый вклад в увеличение $\Omega$. Если Y dx больше, чем $\delta E$ будут собственные состояния энергии, которые движутся снизу E вверх $E+\delta E$. Они учитываются в обоих $N_{Y}\left(E\right)$ и $N_{Y}\left(E+\delta E\right)$, поэтому приведенное выше выражение справедливо и в этом случае.

Выражение приведенного выше выражения как производной по E и суммирование по Y дает выражение:

$\left({\frac {\partial \Omega }{\partial x}}\right)_{E}=-\sum _{Y}Y\left({\frac {\partial \Omega _{Y}}{\partial E}}\right)_{x}=\left({\frac {\partial \left(\Omega X\right)}{\partial E}}\right)_{x}\,$

Логарифмическая производная $\Omega$ относительно x , таким образом, определяется выражением:

$\left({\frac {\partial \ln \left(\Omega \right)}{\partial x}}\right)_{E}=\beta X+\left({\frac {\partial X}{\partial E}}\right)_{x}\,$

Первый член является интенсивным, т.е. он не масштабируется с размером системы. Напротив, последний член масштабируется как обратный размер системы и, таким образом, исчезает в термодинамическом пределе. Таким образом, мы обнаружили, что:

$\left({\frac {\partial S}{\partial x}}\right)_{E}={\frac {X}{T}}\,$

Объединив это с

$\left({\frac {\partial S}{\partial E}}\right)_{x}={\frac {1}{T}}\,$

дает:

$dS=\left({\frac {\partial S}{\partial E}}\right)_{x}dE+\left({\frac {\partial S}{\partial x}}\right)_{E}dx={\frac {dE}{T}}+{\frac {X}{T}}dx={\frac {\delta Q}{T}}\,$

Вывод для систем, описываемых каноническим ансамблем.

Если система находится в тепловом контакте с термостатом при некоторой температуре T , то в равновесии распределение вероятностей по собственным значениям энергии задается каноническим ансамблем :

$P_{j}={\frac {\exp \left(-{\frac {E_{j}}{k_{\mathrm {B} }T}}\right)}{Z}}$

Здесь Z — коэффициент, который нормализует сумму всех вероятностей к 1, эта функция известна как статистическая сумма . Рассмотрим теперь бесконечно малое обратимое изменение температуры и внешних параметров, от которых зависят уровни энергии. Это следует из общей формулы для энтропии:

$S=-k_{\mathrm {B} }\sum _{j}P_{j}\ln \left(P_{j}\right)$

что

$dS=-k_{\mathrm {B} }\sum _{j}\ln \left(P_{j}\right)dP_{j}$

Подставив формулу для $P_{j}$ для канонического ансамбля здесь дает:

$dS={\frac {1}{T}}\sum _{j}E_{j}dP_{j}={\frac {1}{T}}\sum _{j}d\left(E_{j}P_{j}\right)-{\frac {1}{T}}\sum _{j}P_{j}dE_{j}={\frac {dE+\delta W}{T}}={\frac {\delta Q}{T}}$

Начальные условия при Большом взрыве

Как уже говорилось выше, считается, что второй закон термодинамики является результатом начальных условий с очень низкой энтропией при Большом взрыве . Со статистической точки зрения это были совершенно особые условия. С другой стороны, они были довольно простыми, поскольку Вселенная — или, по крайней мере, та ее часть, из которой развилась наблюдаемая Вселенная , — кажется, была чрезвычайно однородной.

Это может показаться несколько парадоксальным, поскольку во многих физических системах однородные состояния (например, смешанные, а не разделенные газы) обладают высокой энтропией. Парадокс разрешается, как только становится понятно, что гравитационные системы имеют отрицательную теплоемкость , поэтому, когда гравитация важна, однородные условия (например, газ однородной плотности) фактически имеют более низкую энтропию по сравнению с неоднородными (например, черные дыры в пустом пространстве). Еще один подход заключается в том, что Вселенная имела высокую (или даже максимальную) энтропию, учитывая ее размер, но по мере роста Вселенной она быстро выходила из термодинамического равновесия, ее энтропия лишь незначительно увеличивалась по сравнению с увеличением максимально возможной энтропии, и, таким образом, она пришел к очень низкой энтропии по сравнению с гораздо большим возможным максимумом, учитывая его более поздний размер.

Что касается причины, по которой начальные условия были такими, одно из предположений заключается в том, что космологической инфляции было достаточно, чтобы стереть негладкость, а другое состоит в том, что Вселенная была создана спонтанно , причем механизм создания предполагает начальные условия с низкой энтропией.

Живые организмы

Существует два основных способа формулирования термодинамики: (а) через переходы из одного состояния термодинамического равновесия в другое и (б) через циклические процессы, при которых система остается неизменной, а общая энтропия окружающей среды увеличивается. Эти два пути помогают понять процессы жизни. Термодинамику живых организмов рассматривали многие авторы, в том числе Эрвин Шредингер (в его книге «Что такое жизнь? ») и Леон Бриллюэн .

В строгом приближении, живые организмы можно рассматривать как примеры (b). Приблизительно физическое состояние животного меняется день ото дня, оставляя животное практически неизменным. Животные поглощают пищу, воду и кислород и в результате обмена веществ выделяют продукты распада и тепло. Растения поглощают лучистую энергию Солнца, которую можно рассматривать как тепло, а также углекислый газ и воду. Они выделяют кислород. Таким образом они растут. В конце концов они умирают, а их останки гниют, превращаясь в основном обратно в углекислый газ и воду. Это можно рассматривать как циклический процесс. В целом, солнечный свет исходит от источника с высокой температурой, Солнца, и его энергия передается поглотителю с более низкой температурой, т.е. излучается в космос. Это увеличение энтропии среды, окружающей растение. Таким образом, животные и растения подчиняются второму закону термодинамики, рассматриваемому с точки зрения циклических процессов.

Более того, способность живых организмов расти и усложняться, а также образовывать связи с окружающей средой в форме приспособления и памяти не противоречит второму закону, а сродни общим результатам, вытекающим из него. : Согласно некоторым определениям, увеличение энтропии также приводит к увеличению сложности. а для конечной системы, взаимодействующей с конечными резервуарами, увеличение энтропии эквивалентно увеличению корреляций между системой и резервуарами.

Живые организмы можно рассматривать как открытые системы, поскольку материя входит в них и выходит из них. Термодинамику открытых систем в настоящее время часто рассматривают с точки зрения переходов из одного состояния термодинамического равновесия в другое или с точки зрения течений в приближении локального термодинамического равновесия. Проблему для живых организмов можно еще больше упростить, приняв приближение устойчивого состояния с неизменными потоками. Общие принципы производства энтропии для таких приближений являются предметом продолжающихся исследований .

Гравитационные системы

Обычно системы, для которых гравитация не важна, имеют положительную теплоемкость , а это означает, что их температура повышается вместе с их внутренней энергией. Следовательно, когда энергия течет от объекта с высокой температурой к объекту с низкой температурой, температура источника уменьшается, а температура стока увеличивается; следовательно, разница температур имеет тенденцию уменьшаться с течением времени.

Это не всегда так для систем, в которых важна гравитационная сила: системы, связанные собственной гравитацией, например звезды, могут иметь отрицательную теплоемкость. По мере их сжатия их общая энергия и энтропия уменьшаются. но их внутренняя температура может увеличиться . Это может быть важно для протозвезд и даже газовых планет-гигантов, таких как Юпитер . Однако если учесть энтропию излучения черного тела, испускаемого телами, можно показать, что общая энтропия системы увеличивается, даже если энтропия планеты или звезды уменьшается.

Неравновесные состояния

Основная статья: Неравновесная термодинамика

Теория классической или равновесной термодинамики идеализируется. Основным постулатом или предположением, часто даже не сформулированным явно, является существование систем в их собственных внутренних состояниях термодинамического равновесия. В общем, область пространства, содержащая физическую систему в данный момент времени, которая может быть найдена в природе, не находится в термодинамическом равновесии, читая в самых строгих терминах. Проще говоря, ничто во всей Вселенной не находится и никогда не находилось в точном термодинамическом равновесии.

Для целей физического анализа часто бывает достаточно сделать предположение о термодинамическом равновесии . Такое предположение может основываться на методе проб и ошибок для своего обоснования. Если предположение оправдано, оно часто может быть очень ценным и полезным, поскольку делает доступной теорию термодинамики. Элементы предположения о равновесии заключаются в том, что система остается неизменной в течение неопределенно длительного времени и что в системе так много частиц, что ее корпускулярную природу можно полностью игнорировать. При таком предположении о равновесии вообще не существует макроскопически обнаруживаемых флуктуаций . Исключение составляют случаи критических состояний , которые невооруженным глазом демонстрируют явление критической опалесценции . Для лабораторных исследований критических состояний необходимы исключительно длительные времена наблюдения.

Во всех случаях сделанное предположение о термодинамическом равновесии, как следствие, подразумевает, что никакая предполагаемая «флуктуация»-кандидат не меняет энтропию системы.

Легко может случиться, что в физической системе происходят внутренние макроскопические изменения, которые происходят достаточно быстро, чтобы сделать недействительным предположение о постоянстве энтропии. Или что в физической системе так мало частиц, что корпускулярная природа проявляется в наблюдаемых флуктуациях. Тогда от предположения о термодинамическом равновесии следует отказаться. Не существует однозначного общего определения энтропии для неравновесных состояний.

Существуют промежуточные случаи, в которых предположение о локальном термодинамическом равновесии является очень хорошим приближением. но, строго говоря, это все же приближение, а не теоретически идеальный вариант.

В целом для неравновесных ситуаций может быть полезно рассмотреть статистические механические определения других величин, которые можно удобно назвать «энтропией», но их не следует путать или объединять с термодинамической энтропией, правильно определенной для второго закона. Эти другие величины действительно принадлежат статистической механике, а не термодинамике, основной области второго закона.

Физика макроскопически наблюдаемых флуктуаций выходит за рамки данной статьи.

Стрела времени

См. Также: Стрела времени и Энтропия (стрела времени).

Второй закон термодинамики — это физический закон, который не симметричен изменению направления времени. Это не противоречит симметриям, наблюдаемым в фундаментальных законах физики (в частности, симметрии CPT ), поскольку второй закон статистически применим к асимметричным во времени граничным условиям. Второй закон был связан с различием между движением вперед и назад во времени или с принципом, согласно которому причина предшествует следствию ( причинная стрела времени , или причинность ).

Необратимость

Необратимость термодинамических процессов является следствием асимметричного характера термодинамических операций, а не каких-либо внутренне необратимых микроскопических свойств тел. Термодинамические операции — это макроскопические внешние вмешательства, налагаемые на участвующие тела, а не вытекающие из их внутренних свойств. Известны «парадоксы», возникающие из-за неспособности признать это.

Парадокс Лошмидта

Основная статья: Парадокс Лошмидта

Парадокс Лошмидта , также известный как парадокс обратимости, представляет собой возражение, согласно которому невозможно вывести необратимый процесс из симметричной во времени динамики, описывающей микроскопическую эволюцию макроскопической системы.

По мнению Шредингера , «теперь совершенно очевидно, каким образом вам следует переформулировать закон энтропии — или, если уж на то пошло, все другие необратимые утверждения — так, чтобы их можно было вывести из обратимых моделей. Вы не должны говорить одной изолированной системы, но по крайней мере двух, которые вы можете на данный момент считать изолированными от остального мира, но не всегда друг от друга». Две системы изолированы друг от друга стеной до тех пор, пока она не будет удалена термодинамической операцией, как это предусмотрено законом. Термодинамическая операция навязывается извне и не подчиняется обратимым микроскопическим динамическим законам, которые управляют составляющими систем. Это причина необратимости. Формулировка закона в настоящей статье соответствует совету Шрёдингера. Причинно-следственная связь логически предшествует второму закону, а не вытекает из него.

Теорема Пуанкаре о возврате

Основная статья: Теорема Пуанкаре о возврате

Теорема о возврате Пуанкаре рассматривает теоретическое микроскопическое описание изолированной физической системы. Это можно рассматривать как модель термодинамической системы после того, как в результате термодинамической операции была удалена внутренняя стенка. Система через достаточно долгое время вернется в микроскопически определенное состояние, очень близкое к исходному. Время возврата Пуанкаре — это время, прошедшее до возвращения. Он чрезвычайно длинный, вероятно, дольше, чем срок жизни Вселенной, и сильно зависит от геометрии стены, которая была удалена в результате термодинамической операции. Теорему о возврате можно воспринимать как явно противоречащую второму закону термодинамики. Однако более очевидно, что это просто микроскопическая модель термодинамического равновесия в изолированной системе, образовавшейся в результате удаления стенки между двумя системами. Для типичной термодинамической системы время возврата настолько велико (во много раз превышает время жизни Вселенной), что для всех практических целей невозможно наблюдать возвращение. Тем не менее можно было бы представить, что можно дождаться повторения Пуанкаре, а затем снова вставить стенку, удаленную термодинамической операцией. Тогда очевидно, что появление необратимости обусловлено полной непредсказуемостью возврата Пуанкаре, если только исходное состояние было состоянием термодинамического равновесия, как это имеет место в макроскопической термодинамике. Даже если бы можно было дождаться этого, у него нет практической возможности выбрать правильный момент, в который можно снова вставить стену. Теорема Пуанкаре о возврате дает решение парадокса Лошмидта. Если бы изолированную термодинамическую систему можно было контролировать в течение все большего числа кратных среднего времени повторения Пуанкаре, термодинамическое поведение системы стало бы инвариантным при обращении времени.

Джеймс Клерк Максвелл

Демон Максвелла

Основная статья: Демон Максвелла

Джеймс Клерк Максвелл разделенный на две части: А и Б. представил себе один контейнер , Обе части заполнены одним и тем же газом при равных температурах и расположены рядом друг с другом, разделенные перегородкой. Наблюдая за молекулами с обеих сторон, воображаемый демон охраняет микроскопический люк в стене. быстрее средней, Когда молекула из А, летит к люку, демон открывает его, и молекула полетит из А в Б. движущаяся Средняя скорость молекул в B увеличится, тогда как в A они в среднем замедлятся. Поскольку средняя скорость молекул соответствует температуре, температура уменьшается в A и увеличивается в B , что противоречит второму закону термодинамики.

Один ответ на этот вопрос был предложен в 1929 году Лео Силардом , а затем Леоном Бриллюэном . Сцилард отметил, что реальный демон Максвелла должен иметь какие-то средства измерения скорости молекул и что получение информации потребует затрат энергии. Точно так же Бриллюэн продемонстрировал, что уменьшение энтропии, вызванное демоном, будет меньше, чем энтропия, возникающая при выборе молекул на основе их скорости.

Максвелла неоднократно изменяет проницаемость стены между А и В. «Демон » Таким образом, он выполняет термодинамические операции в микроскопическом масштабе, а не просто наблюдает обычные спонтанные или естественные макроскопические термодинамические процессы.

Котировки

Закон, согласно которому энтропия всегда возрастает, занимает, я думаю, высшее положение среди законов Природы . Если кто-то укажет вам, что ваша любимая теория Вселенной не согласуется с уравнениями Максвелла – тем хуже для уравнений Максвелла. Если окажется, что это противоречит наблюдениям – что ж, эти экспериментаторы иногда что-то путают. Но если окажется, что ваша теория противоречит второму началу термодинамики, я не могу дать вам никакой надежды; ему ничего не остается, кроме как рухнуть в глубочайшем унижении.

- Сэр Артур Стэнли Эддингтон , Природа физического мира (1927)

Формулировок второго закона было почти столько же, сколько его дискуссий.

— Философ/физик П.В. Бриджмен (1941).

Клаузиус является автором сивиллического высказывания: «Энергия Вселенной постоянна; энтропия Вселенной стремится к максимуму». Цели термомеханики континуума далеки от объяснения «вселенной», но в рамках этой теории мы можем легко получить явное утверждение, в чем-то напоминающее Клаузиуса, но относящееся только к скромному объекту: изолированному телу конечного размера.

- Трусделл, К. , Манкастер, Р.Г. (1980). Основы кинетической теории Максвелла простого одноатомного газа, рассматриваемой как раздел рациональной механики , Academic Press, Нью-Йорк, ISBN   0-12-701350-4 , с. 17.

См. также

• Нулевой закон термодинамики
• Первый закон термодинамики
• Третий закон термодинамики
• Неравенство Клаузиуса – Дюэма
• Теорема о флуктуациях
• Тепловая смерть Вселенной
• История термодинамики
• Равенство Яржинского
• Законы термодинамики
• Термодинамика максимальной энтропии
• Квантовая термодинамика
• Размышления о движущей силе огня
• Релятивистская теплопроводность
• Термический диод
• Термодинамическое равновесие

Ссылки

Источники

• Адкинс, CJ (1983). Равновесная термодинамика (1-е изд. 1968 г., 3-е изд.). Кембридж, Великобритания: Издательство Кембриджского университета. ISBN  0-521-25445-0 . ОСЛК   9132054 .
• Аткинс, П.В. , де Паула, Дж. (2006). Физическая химия Аткинса , восьмое издание, WH Freeman, Нью-Йорк, ISBN   978-0-7167-8759-4 .
• Аттард, П. (2012). Неравновесная термодинамика и статистическая механика: основы и приложения , Oxford University Press, Оксфорд, Великобритания, ISBN   978-0-19-966276-0 .
• Байерляйн, Р. (1999). Теплофизика , Издательство Кембриджского университета, Кембридж, Великобритания, ISBN   0-521-59082-5 .
• Бейлин, М. (1994). Обзор термодинамики , Американский институт физики, Нью-Йорк, ISBN   0-88318-797-3 .
• Бланделл, Стивен Дж .; Бланделл, Кэтрин М. (2010). Понятия теплофизики (2-е изд.). Оксфорд: Издательство Оксфордского университета . doi : 10.1093/acprof:oso/9780199562091.001.0001 . ISBN  9780199562107 . OCLC   607907330 .
• Больцманн, Л. (1896/1964). Лекции по теории газа , перевод С.Г. Браша, Калифорнийский университет, Беркли.
• Боргнакке, К., Sonntag., RE (2009). Основы термодинамики , седьмое издание, Уайли, ISBN   978-0-470-04192-5 .
• Бухдал, ХА (1966). Концепции классической термодинамики , Издательство Кембриджского университета, Кембридж, Великобритания.
• Бриджмен, военнопленный (1943). Природа термодинамики , Издательство Гарвардского университета, Кембридж, Массачусетс.
• Каллен, Х.Б. (1960/1985). Термодинамика и введение в термостатистику , (1-е издание, 1960 г.), 2-е издание, 1985 г., Уайли, Нью-Йорк, ISBN   0-471-86256-8 .
• К. Каратеодори (1909). «Исследования по основам термодинамики» . Математические летописи . 67 (3): 355–386. дои : 10.1007/bf01450409 . S2CID   118230148 . Архивировано из оригинала 4 марта 2016 г. Проверено 18 февраля 2014 г. Аксиома II: В любой среде с произвольно заданным начальным состоянием существуют состояния, которые не могут быть произвольно аппроксимированы адиабатическими изменениями состояния. (с.363) . Перевод можно найти здесь . Также наиболее надежный перевод можно найти у Кестина Дж. (1976). Второй закон термодинамики , Дауден, Хатчинсон и Росс, Страудсбург, Пенсильвания.
• Карно, С. (1824/1986). Размышления о движущей силе огня , Издательство Манчестерского университета, Манчестер, Великобритания, ISBN   0-7190-1741-6 . Также здесь.
• Чепмен, С. , Коулинг, Т.Г. (1939/1970). Математическая теория неоднородных газов. Отчет о кинетической теории вязкости, теплопроводности и диффузии в газах , третье издание, 1970 г., Cambridge University Press, Лондон.
• Клаузиус, Р. (1850). «О движущей силе тепла и о законах, которые можно вывести из нее для теории самой теплоты» . Анналы физики . 79 (4): 368–397, 500–524. Бибкод : 1850АнП...155..500С . дои : 10.1002/andp.18501550403 . hdl : 2027/uc1.$b242250 . Проверено 26 июня 2012 г. В переводе на английский: Клаузиус, Р. (июль 1851 г.). «О движущей силе тепла и вытекающих из нее законах природы самой теплоты» . Философский журнал и журнал науки Лондона, Эдинбурга и Дублина . 4-й. 2 (VIII): 1–21, 102–119. дои : 10.1080/14786445108646819 . Проверено 26 июня 2012 г.
• Клаузиус, Р. (1854 г.). «О модифицированной форме второго закона механической теории теплоты» (PDF) . Анналы физики . xciii (12): 481–506. Бибкод : 1854АнП...169..481С . дои : 10.1002/andp.18541691202 . Архивировано из оригинала (PDF) 24 марта 2014 года . Проверено 24 марта 2014 г. В переводе на английский: Клаузиус, Р. (июль 1856 г.). «О модифицированной форме второй основной теоремы механической теории теплоты» . Философский журнал и журнал науки Лондона, Эдинбурга и Дублина . 4-й. 2:86 ​ . Проверено 24 марта 2014 г. Перепечатано в: Клаузиус, Р. (1867). Механическая теория тепла - с ее приложениями к паровому двигателю и физическим свойствам тел . Лондон: Джон ван Ворст . Проверено 19 июня 2012 г. редакции: PwR_Sbkwa8IC.
• Денби, К. (1954/1981). Принципы химического равновесия. С приложениями в химии и химической инженерии , четвертое издание, издательство Кембриджского университета, Кембридж, Великобритания, ISBN   0-521-23682-7 .
• Эу, Британская Колумбия (2002). Обобщенная термодинамика. Термодинамика необратимых процессов и обобщенная гидродинамика , Kluwer Academic Publishers, Дордрехт, ISBN   1-4020-0788-4 .
• Гиббс, Дж.В. (1876/1878). О равновесии гетерогенных веществ, Пер. конн. акад. , 3 : 108–248, 343–524, перепечатано в «Собрании сочинений Дж. Уилларда Гиббса, доктора философии, магистра права». D. , под редакцией WR Longley, RG Van Name, Longmans, Green & Co., Нью-Йорк, 1928, том 1, стр. 55–353.
• Грим, HR (2005). Принципы плазменной спектроскопии (Кембриджские монографии по физике плазмы) , издательство Кембриджского университета, Нью-Йорк ISBN   0-521-61941-6 .
• Глансдорф П., Пригожин И. (1971). Термодинамическая теория структуры, стабильности и флуктуаций , Wiley-Interscience, Лондон, 1971, ISBN   0-471-30280-5 .
• Гранди, Уолтер Т. (2008). Энтропия и временная эволюция макроскопических систем . Оксфорд, Нью-Йорк: Издательство Оксфордского университета. ISBN  978-0-19-954617-6 . OCLC   190843367 .
• Гревен А., Келлер Г., Варнеке (редакторы) (2003). Энтропия , Издательство Принстонского университета, Принстон, Нью-Джерси, ISBN   0-691-11338-6 .
• Гуггенхайм, Э.А. (1949). «Статистические основы термодинамики», Исследования , 2 : 450–454.
• Гуггенхайм, Э.А. (1967). Термодинамика. Расширенное лечение для химиков и физиков , пятое исправленное издание, Северная Голландия, Амстердам.
• Дьярмати, И. (1967/1970) Неравновесная термодинамика. Теория поля и вариационные принципы , перевод Э. Дьярмати и В. Ф. Хайнца, Спрингер, Нью-Йорк.
• Киттель, К. , Кремер, Х. (1969/1980). Теплофизика , второе издание, Фриман, Сан-Франциско, Калифорния, ISBN   0-7167-1088-9 .
• Кондепуди Д., Пригожин И. (1998). Современная термодинамика: от тепловых двигателей к диссипативным структурам , John Wiley & Sons, Чичестер, ISBN   0-471-97393-9 .
• Лебон Г., Жу Д., Касас-Васкес Дж. (2008). Понимание неравновесной термодинамики: основы, приложения, границы , Springer-Verlag, Берлин, ISBN   978-3-540-74252-4 .
• Либ, Э.Х.; Ингвасон, Дж. (1999). «Физика и математика второго закона термодинамики». Отчеты по физике . 310 (1): 1–96. arXiv : cond-mat/9708200 . Бибкод : 1999PhR...310....1L . дои : 10.1016/S0370-1573(98)00082-9 . S2CID   119620408 .
• Либ Э.Х., Ингвасон Дж. (2003). Энтропия классической термодинамики, стр. 147–195, глава 8 книги «Энтропия» , Гревен А., Келлер Г., Варнеке (редакторы) (2003).
• Мандл, Ф. (1988). Статистическая физика (второе изд.). Уайли и сыновья . ISBN  978-0-471-91533-1 .
• Максвелл, Дж. К. (1867). «К динамической теории газов». Фил. Пер. Р. Сок. Лонд . 157 : 49–88. дои : 10.1098/rstl.1867.0004 . S2CID   96568430 .
• Мюллер, И. (1985). Термодинамика , Питман, Лондон, ISBN   0-273-08577-8 .
• Мюллер, И. (2003). Энтропия в неравновесии, стр. 79–109, глава 5 книги «Энтропия» , Гревен А., Келлер Г., Варнеке (редакторы) (2003).
• Мюнстер, А. (1970), Классическая термодинамика , перевод Э. С. Хальберштадта, Wiley – Interscience, Лондон, ISBN   0-471-62430-6 .
• Пиппард, AB (1957/1966). Элементы классической термодинамики для студентов-физиков , оригинальная публикация 1957 г., переиздание 1966 г., Cambridge University Press, Кембридж, Великобритания.
• Планк, М. (1897/1903). Трактат по термодинамике , перевод А. Огга, Лонгманс Грин, Лондон, с. 100.
• Планк. М. (1914). Теория теплового излучения , перевод Масиуса М. второго немецкого издания, P. Blakiston's Son & Co., Филадельфия.
• Планк, М. (1926). Об обосновании второго закона термодинамики, Труды Прусской академии наук: Физико-математический класс : 453–463.
• Покровский В.Н. (2005) Расширенная термодинамика в дискретно-системном подходе, Евр. Дж. Физ. том. 26, 769–781.
• Покровский, Владимир Н. (2013). «Вывод основных соотношений неравновесной термодинамики» . ISRN Термодинамика . 2013 : 1–9. дои : 10.1155/2013/906136 .
• Куинн, Ти Джей (1983). Температура , Academic Press, Лондон, ISBN   0-12-569680-9 .
• Рао, YVC (2004). Введение в термодинамику . Университетская пресса. п. 213. ИСБН  978-81-7371-461-0 .
• Робертс, Дж. К., Миллер, А. Р. (1928/1960). Тепло и термодинамика (первое издание, 1928 г.), пятое издание, Blackie & Son Limited, Глазго.
• Шредингер, Э. (1950). Необратимость, Учеб. Р. Ир. акад. , А53 : 189–195.
• тер Хаар, Д. , Вергеланд, Х. (1966). Элементы термодинамики , издательство Addison-Wesley Publishing, Reading MA.
• Томсон, В. (1851). «О динамической теории тепла с численными результатами, полученными на основе эквивалента тепловой единицы г-на Джоуля, и наблюдений г-на Рено над паром» . Труды Королевского общества Эдинбурга . XX (часть II): 261–268, 289–298. Также опубликовано в Томсон, В. (декабрь 1852 г.). «О динамической теории тепла с численными результатами, полученными на основе эквивалента тепловой единицы г-на Джоуля, и наблюдений г-на Рено над паром» . Филос. Маг . 4. IV (22): 13 . Проверено 25 июня 2012 г.
• Томсон, В. (1852 г.). О всеобщей тенденции в природе к рассеянию механической энергии Философский журнал, сер. 4, с. 304.
• Тиса, Л. (1966). Обобщенная термодинамика , MIT Press, Кембридж, Массачусетс.
• Трусделл, К. (1980). Трагикомическая история термодинамики 1822–1854 гг. , Спрингер, Нью-Йорк, ISBN   0-387-90403-4 .
• Уффинк, Дж. (2001). Блефуйте во втором законе термодинамики, Стад. Хист. Фил. Мод. Физ. , 32 (3): 305–394.
• Уффинк, Дж. (2003). Необратимость и второй закон термодинамики, Глава 7 книги «Энтропия» , Гревен А., Келлер Г., Варнеке (редакторы) (2003), Princeton University Press, Принстон, Нью-Джерси, ISBN   0-691-11338-6 .
• Уленбек, Дж. Э. , Форд, Г. В. (1963). Лекции по статистической механике , Американское математическое общество, Провиденс, Род-Айленд.
• Земанский, М.В. (1968). Тепло и термодинамика. Учебник для среднего уровня , пятое издание, McGraw-Hill Book Company, Нью-Йорк.

Дальнейшее чтение

• Гольдштейн, Мартин и Инге Ф., 1993. Холодильник и Вселенная . Гарвардский университет. Нажимать. Глава. 4–9 содержат введение ко Второму закону, немного менее техническое, чем эта статья. ISBN   978-0-674-75324-2
• Лефф, Харви С. и Рекс, Эндрю Ф. (ред.) 2003. Демон Максвелла 2: Энтропия, классическая и квантовая информация, вычисления . Бристоль Великобритания; Филадельфия, Пенсильвания: Институт физики . ISBN   978-0-585-49237-7
• Холливелл, Джей-Джей (1994). Физические причины асимметрии времени . Кембридж. ISBN  978-0-521-56837-1 . (технический).
• Карно, Сади (1890). Терстон, Роберт Генри (ред.). Размышления о движущей силе тепла и о машинах, способных развивать эту силу . Нью-Йорк: Дж. Уайли и сыновья. ( полный текст изд. 1897 г. ) ( html. Архивировано 18 августа 2007 г. в Wayback Machine )
• Стивен Джей Клайн (1999). Краткие сведения об энтропии и интерпретационная термодинамика , Ла-Каньяда, Калифорния: DCW Industries. ISBN   1-928729-01-0 .
• Костич, М (2011). Возвращаясь ко второму закону деградации энергии и генерации энтропии: от гениальных рассуждений Сади Карно к целостному обобщению . Материалы конференции AIP. Том. 1411. стр. 327–350. Бибкод : 2011AIPC.1411..327K . CiteSeerX   10.1.1.405.1945 . дои : 10.1063/1.3665247 . ISBN  978-0-7354-0985-9 . {{cite book}}: |journal= игнорируется ( помощь ) также в [1] .

Внешние ссылки

• Стэнфордская энциклопедия философии : « Философия статистической механики » - Лоуренс Склар.
• Второй закон термодинамики в курсе Массачусетского технологического института «Единая термодинамика и движение» от профессора З.С. Спаковского
• ET Jaynes , 1988, « Эволюция принципа Карно », в книге GJ Erickson и CR Smith (ред.) «Максимальная энтропия и байесовские методы в науке и технике» , Vol.1: p. 267.
• Каратеодори, К., «Исследование основ термодинамики», пер. от Д. Х. Дельфениха
• Второй закон термодинамики , обсуждение BBC Radio 4 с Джоном Гриббином, Питером Аткинсом и Моникой Грейди ( «В наше время» , 16 декабря 2004 г.)
• Журнал Международного общества истории философии науки, 2012 г.