Фермент, ограниченный диффузией
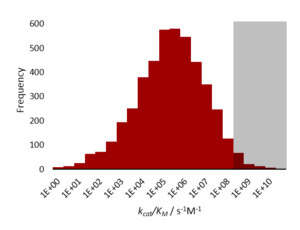
Фермент , ограниченный диффузией, катализирует реакцию настолько эффективно, что стадией, лимитирующей скорость, является субстрата диффузия в активный центр или диффузия продукта наружу. [ 2 ] Это также известно как кинетическое совершенство или каталитическое совершенство . Поскольку скорость катализа таких ферментов определяется реакцией, контролируемой диффузией , она представляет собой внутреннее физическое ограничение эволюции (максимальная высота пика в ландшафте приспособленности ). Совершенные ферменты, ограниченные диффузией, встречаются очень редко. Большинство ферментов катализируют свои реакции со скоростью, которая в 1 000–10 000 раз медленнее этого предела. Это связано как с химическими ограничениями сложных реакций, так и с эволюционными ограничениями, заключающимися в том, что такие высокие скорости реакций не придают никакой дополнительной приспособленности . [ 1 ]
История
[ редактировать ]
Теория реакции, контролируемой диффузией, первоначально использовалась Р. А. Альберти, Гордоном Хаммесом и Манфредом Эйгеном для оценки верхнего предела фермент-субстратной реакции. [ 3 ] [ 4 ] По их оценке, [ 3 ] [ 4 ] верхний предел фермент-субстратной реакции составлял 10 9 М −1 с −1 .
В 1972 году было замечено, что при дегидратации H 2 CO 3 , катализируемой карбоангидразой , константа скорости второго порядка, полученная экспериментально, составила около 1,5×10. 10 М −1 с −1 , [ 5 ] что на порядок выше верхнего предела, оцененного Альберти, Хаммесом и Эйгеном на основе упрощенной модели. [ 3 ] [ 4 ]
Чтобы разрешить такой парадокс, Куо-Чен Чоу и его коллеги предложили модель, учитывающую пространственный фактор и фактор силового поля между ферментом и его субстратом, и обнаружили, что верхний предел может достигать 10 10 М −1 с −1 , [ 6 ] [ 7 ] [ 8 ] и может быть использован для объяснения некоторых удивительно высоких скоростей реакций в молекулярной биологии. [ 5 ] [ 9 ] [ 10 ]
Новый верхний предел, найденный Chou et al. Фермент-субстратная реакция была дополнительно обсуждена и проанализирована в серии последующих исследований. [ 11 ] [ 12 ] [ 13 ]
Подробное сравнение упрощенной модели Альберти-Хаммеса-Эйгена ( а ) и модели Чжоу ( б ) при расчете скорости диффузионно-контролируемой реакции фермента с его субстратом, или верхнего предела фермент-субстратной реакции, было подробно рассмотрено в работе бумага. [ 14 ]
Механизм
[ редактировать ]совершенные ферменты имеют специфичности kcat . / Кинетически Km константу порядка 10 8 до 10 9 М −1 с −1 . Скорость катализируемой ферментом реакции ограничена диффузией , поэтому фермент «обрабатывает» субстрат задолго до того, как он встретит другую молекулу. [ 1 ]
Некоторые ферменты действуют с кинетикой, превышающей скорость диффузии, что кажется невозможным. Для объяснения этого явления было задействовано несколько механизмов. Считается, что некоторые белки ускоряют катализ, втягивая субстрат и предварительно ориентируя его с помощью диполярных электрических полей. Некоторые ссылаются на квантово-механическое объяснение туннелирования , согласно которому протон или электрон могут туннелировать через активационные барьеры. Если теория туннелирования протонов оставалась спорной идеей, [ 15 ] [ 16 ] Было доказано, что это единственно возможный механизм в случае липоксигеназы сои. [ 17 ]
Эволюция
[ редактировать ]Стоит отметить, что кинетически совершенных ферментов не так много. Это можно объяснить с точки зрения естественного отбора . Увеличение каталитической скорости может быть предпочтительным, поскольку оно может дать организму некоторые преимущества. Однако когда каталитическая скорость превышает скорость диффузии (т. е. субстраты входят в активный центр и покидают его, а также сталкиваются с субстратами), нет больше смысла увеличивать скорость еще больше. Предел диффузии представляет собой абсолютное физическое ограничение эволюции. [ 1 ] Увеличение каталитической скорости сверх скорости диффузии никоим образом не поможет организму и поэтому представляет собой глобальный максимум в фитнес-ландшафте . Следовательно, эти совершенные ферменты, должно быть, возникли в результате «счастливой» случайной мутации , которая случайно распространилась, или потому, что более высокая скорость когда-то была полезна как часть другой реакции в предках фермента. [ нужна ссылка ]
Примеры
[ редактировать ]- Ацетилхолинэстераза
- β-лактамаза
- Каталаза
- Карбоангидраза
- Дегидрогеназа угарного газа [ 18 ]
- Цитохром с пероксидаза
- Фумараза
- Супероксиддисмутаза
- Триозофосфат-изомераза
См. также
[ редактировать ]Ссылки
[ редактировать ]- ^ Jump up to: а б с д Бар-Эвен, Аррен; Нур, Элад; Савир, Йонатан; Либермейстер, Вольфрам; Давиди, Дэн; Тауфик, Дэн С; Майло, Рон (2011). «Умеренно эффективный фермент: эволюционные и физико-химические тенденции, определяющие параметры фермента». Биохимия . 50 (21): 4402–10. дои : 10.1021/bi2002289 . ПМИД 21506553 .
- ^ Берг, Джереми М.; Тимочко, Дж.Л.; Страйер, Л. (2006). «Окислительное фосфорилирование». Биохимия (5-е изд.). стр. 491–526. ISBN 978-0716787242 .
- ^ Jump up to: а б с Альберти, Роберт А.; Хаммес, Гордон Г. (1958). «Применение теории диффузионно-контролируемых реакций к кинетике ферментов». Журнал физической химии . 62 (2): 154–9. дои : 10.1021/j150560a005 .
- ^ Jump up to: а б с Эйген, Манфред; Хаммес, Гордон Г. (2006). «Элементарные этапы ферментативных реакций (по данным релаксационной спектрометрии)». В Норде, FF (ред.). Достижения энзимологии и смежных областей молекулярной биологии . Том. 25. стр. 1–38. дои : 10.1002/9780470122709.ch1 . ISBN 978-0-470-12270-9 . OCLC 777630506 . ПМИД 14149678 .
{{cite book}}:|journal=игнорируется ( помогите ) - ^ Jump up to: а б Кениг, Сеймур Х.; Браун, Родни Д. (1972). «H 2 CO 3 как субстрат карбоангидразы при дегидратации HCO 3 − " . Proceedings of the National Academy of Sciences of the United States of America . 69 (9): 2422–5. Бибкод : ...69.2422K . doi : 10.1073/pnas.69.9.2422 . JSTOR 61783. 1972PNAS PMC 426955 . ПМИД 4627028 .
- ^ Чжоу, Го-Чен; Цзян, Шоу-Пин (1974). «Исследование скорости диффузионно-контролируемых реакций ферментов. Пространственный фактор и фактор силового поля». Scientia Sinica . 27 (5): 664–80. ПМИД 4219062 .
- ^ Чоу, Го-Чен (1976). «Кинетика реакции сочетания фермента и субстрата». Scientia Sinica . 19 (4): 505–28. ПМИД 824728 .
- ^ Ли, ТТ; Чоу, К.К. (1976). «Количественные связи между скоростью диффузионно-контролируемой реакции и характеристическими параметрами в фермент-субстратных реакционных системах. I. Нейтральные субстраты». Scientia Sinica . 19 (1): 117–36. ПМИД 1273571 .
- ^ Риггс, Артур Д.; Буржуа, Сюзанна; Кон, Мелвин (1970). «Взаимодействие лакового репрессора и оператора». Журнал молекулярной биологии . 53 (3): 401–17. дои : 10.1016/0022-2836(70)90074-4 . ПМИД 4924006 .
- ^ Киршнер, Каспер; Гальего, Эрнесто; Шустер, Инге; Гудолл, Дэвид (1971). «Кооперативное связывание никотинамидадениндинуклеотида с глицеральдегид-3-фосфатдегидрогеназой дрожжей». Журнал молекулярной биологии . 58 (1): 29–50. дои : 10.1016/0022-2836(71)90230-0 . ПМИД 4326080 .
- ^ Чжоу, Го Чен; Чжоу, Го Пин (1982). «Роль белка вне активного центра в реакции ферментов, контролируемой диффузией». Журнал Американского химического общества . 104 (5): 1409–1413. дои : 10.1021/ja00369a043 .
- ^ Пайенс, ТАД (1983). «Почему ферменты такие большие?». Тенденции биохимических наук . 8 (2): 46. дои : 10.1016/0968-0004(83)90382-1 .
- ^ Чжоу, Гожи; Вонг, Минг-Тат; Чжоу, Го-Цян (1983). «Диффузионно-контролируемые реакции ферментов». Биофизическая химия . 18 (2): 125–32. дои : 10.1016/0301-4622(83)85006-6 . ПМИД 6626685 .
- ^ Чжоу, Го-Цян; Чжун, Вэй-Чжу (1982). «Диффузионно-контролируемые реакции ферментов». Европейский журнал биохимии . 128 (2–3): 383–7. дои : 10.1111/j.1432-1033.1982.tb06976.x . ПМИД 7151785 .
- ^ Гарсиа-Вилока, М; Гао, Цзяли; Карплюс, Мартин; Трулар, Дональд Дж. (2004). «Как работают ферменты: анализ с помощью современной теории скорости и компьютерного моделирования». Наука . 303 (5655): 186–95. Бибкод : 2004Sci...303..186G . дои : 10.1126/science.1088172 . ПМИД 14716003 . S2CID 17498715 .
- ^ Олссон, Матс Х.М.; Зигбан, Пер EM; Варшел, Арье (2004). «Моделирование большого кинетического изотопного эффекта и температурной зависимости переноса атома водорода в липоксигеназе». Журнал Американского химического общества . 126 (9): 2820–8. дои : 10.1021/ja037233l . ПМИД 14995199 .
- ^ Евтич, С; Андерс, Дж (2017). «Качественная модель квантовой скорости переноса водорода в липоксигеназе сои». Журнал химической физики . 147 (11): 114108. arXiv : 1612.03773 . Бибкод : 2017JChPh.147k4108J . дои : 10.1063/1.4998941 . ПМИД 28938801 . S2CID 11202267 .
- ^ Домник, Лилит; Мерруш, Мерием; Гетцль, Себастьян; Чон, Джэ Хун; Леже, Кристоф; Дементен, Себастьен; Фурмонд, Винсент; Доббек, Хольгер (27 ноября 2017 г.). «CODH-IV: высокоэффективная CO-удаляющая CO-дегидрогеназа, устойчивая к O2» (PDF) . Angewandte Chemie, международное издание . 56 (48): 15466–15469. дои : 10.1002/anie.201709261 . ISSN 1521-3773 . ПМИД 29024326 .