Твердотельное моделирование

Геометрия при твердотельном моделировании полностью описывается в трехмерном пространстве; объекты можно рассматривать под любым углом.

Твердотельное моделирование (или твердотельное моделирование ) — это последовательный набор принципов математического и компьютерного моделирования трехмерных форм (твердых тел) . Твердотельное моделирование выделяется в более широких смежных областях геометрического моделирования и компьютерной графики , таких как 3D-моделирование , своим акцентом на физическую точность. ^[1] Вместе принципы геометрического и твердотельного моделирования составляют основу автоматизированного 3D-проектирования и в целом поддерживают создание, обмен, визуализацию, анимацию, опрос и аннотирование цифровых моделей физических объектов.

Обзор

Использование методов твердотельного моделирования позволяет автоматизировать процесс ряда сложных инженерных расчетов, выполняемых в рамках процесса проектирования. Моделирование, планирование и проверка таких процессов, как механическая обработка и сборка, были одними из основных катализаторов развития твердотельного моделирования. Совсем недавно диапазон поддерживаемых производственных приложений был значительно расширен и теперь включает листового металла производство , литье под давлением , сварку , прокладку труб и т. д. Помимо традиционного производства, методы твердотельного моделирования служат основой для быстрого прототипирования , архивирования цифровых данных и обратного проектирования. путем реконструкции твердых тел по выборочным точкам на физических объектах, механического анализа с использованием конечных элементов , планирования движения и проверки траектории ЧПУ, кинематического и динамического анализа и механизмов так далее. Центральной проблемой всех этих приложений является способность эффективно представлять трехмерную геометрию и манипулировать ею таким образом, чтобы это соответствовало физическому поведению реальных артефактов. Исследования и разработки твердотельного моделирования эффективно решили многие из этих проблем и продолжают оставаться в центре внимания компьютерное проектирование .

Математические основы

Понятие твердотельного моделирования, практикуемое сегодня, основано на конкретной потребности в информационной полноте в системах механического геометрического моделирования в том смысле, что любая компьютерная модель должна поддерживать все геометрические запросы, которые могут быть заданы к соответствующему физическому объекту. Это требование неявно признает возможность существования нескольких компьютерных представлений одного и того же физического объекта при условии, что любые два таких представления непротиворечивы. Невозможно вычислительно проверить информационную полноту представления, если понятие физического объекта не определено в терминах вычислимых математических свойств и не зависит от какого-либо конкретного представления. Такие рассуждения привели к развитию парадигмы моделирования, которая сформировала область твердотельного моделирования, какой мы ее знаем сегодня. ^[2]

Все производимые компоненты имеют конечный размер и хорошо управляемые границы , поэтому изначально основное внимание уделялось математическому моделированию жестких деталей из однородного изотропного материала, которые можно было добавлять или удалять. Эти постулированные свойства можно перевести в свойства регионов , подмножеств трехмерного евклидова пространства . Два распространенных подхода к определению «солидности» основаны на топологии множества точек и алгебраической топологии соответственно. Обе модели определяют, как твердые тела могут быть построены из простых частей или ячеек.

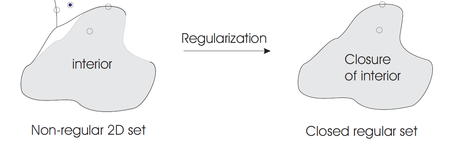
Регуляризация двумерного набора путем замыкания его внутренней части.

Согласно модели сплошности континуального множества точек, все точки любого X ⊂ ℝ ³ могут быть классифицированы в соответствии с их окрестностями относительно X как внутренние , внешние или граничные точки. Предполагая ℝ ³ наделена типичной евклидовой метрикой , окрестность точки p ∈ X принимает форму открытого шара . Чтобы X считалось твердым, каждая окрестность любого p ∈ X должна быть последовательно трехмерной; точки с окрестностями меньшей размерности указывают на отсутствие прочности. Размерная однородность окрестностей гарантируется для класса замкнутых регулярных множеств , определяемых как множества, равные замыканию их внутренности. Любой X ⊂ ℝ ³ может быть превращено в замкнутое регулярное множество или «регуляризовано», замыкая его внутреннюю часть, и, таким образом, пространство моделирования твердых тел математически определяется как пространство замкнутых регулярных подмножеств ℝ ³ (по теореме Гейне-Бореля подразумевается, что все тела являются компактами ). Кроме того, твердые тела должны быть замкнуты с помощью логических операций объединения, пересечения и разности множеств (чтобы гарантировать целостность после добавления и удаления материала). Применение стандартных логических операций к закрытым регулярным множествам может не привести к созданию замкнутого регулярного множества, но эту проблему можно решить путем регуляризации результата применения стандартных логических операций. ^[3] Регуляризованные операции над множествами обозначаются ∪ ^∗, ∩ ^∗, и — ^∗.

Комбинаторная характеризация множества X ⊂ ℝ ³ в качестве твердого тела предполагает представление X как ориентируемого комплекса ячеек , так что ячейки обеспечивают конечные пространственные адреса для точек в бесчисленном в противном случае континууме. ^[1] Класс полуаналитических ограниченных подмножеств евклидова пространства замкнут относительно булевых операций (стандартных и регуляризованных) и обладает дополнительным свойством, заключающимся в том, что каждое полуаналитическое множество можно расслоить на набор непересекающихся ячеек размерностей 0,1,2,3. . Триангуляция , полуаналитического набора в набор точек, отрезков линий треугольных граней и тетраэдрических элементов является примером часто используемой стратификации. Затем комбинаторную модель твердости резюмируют, говоря, что твердые тела не только являются полуаналитическими ограниченными подмножествами, но и представляют собой трехмерные топологические многогранники , а именно трехмерные ориентируемые многообразия с краем. ^[4] В частности, отсюда следует эйлерова характеристика комбинаторной границы ^[5] многогранника равно 2. Комбинаторная модель многообразия твердости также гарантирует, что граница твердого тела разделяет пространство ровно на два компонента как следствие теоремы Жордана-Брауэра , тем самым исключая множества с немногообразными окрестностями, которые считаются невозможными для изготовления.

Точечные и комбинаторные модели твердых тел полностью согласуются друг с другом, могут использоваться взаимозаменяемо, полагаясь при необходимости на континуальные или комбинаторные свойства, и могут быть расширены до n измерений. Ключевое свойство, обеспечивающее эту согласованность, состоит в том, что класс замкнутых регулярных подмножеств ℝ ^н в точности совпадает с однородно n -мерными топологическими многогранниками. Следовательно, каждое n -мерное тело может быть однозначно представлено своей границей, а граница имеет комбинаторную структуру n-1 -мерного многогранника, имеющего однородно n-1 -мерные окрестности.

Твердые схемы представления

Любая схема изображения твердых тел, основанная на предполагаемых математических свойствах, представляет собой метод сбора информации о классе полуаналитических подмножеств евклидова пространства. Это означает, что все представления представляют собой разные способы организации одних и тех же геометрических и топологических данных в форме структуры данных . Все схемы представления организованы с помощью конечного числа операций над множеством примитивов. Пространство моделирования любого конкретного представления конечно, и какой-либо одной схемы представления может быть недостаточно для представления всех типов твердых тел. Например, твердые тела, определенные с помощью комбинаций регуляризованных логических операций, не обязательно могут быть представлены как движение примитива, движущегося по пространственной траектории, за исключением очень простых случаев. Это вынуждает современные системы геометрического моделирования поддерживать несколько схем представления твердых тел, а также способствовать эффективному преобразованию между схемами представления.

techniques used to create or represent solid models.^[4] Modern modeling software may use a combination of these schemes to represent a solid.

Примитивное создание экземпляров

Эта схема основана на понятии семейств объектов, каждый член семейства отличается от другого по нескольким параметрам. Каждое семейство объектов называется универсальным примитивом , а отдельные объекты внутри семейства называются экземплярами примитива . Например, семейство болтов является универсальным примитивом, а отдельный болт, заданный определенным набором параметров, является экземпляром примитива. Отличительной характеристикой чисто параметризованных схем создания экземпляров является отсутствие средств для объединения экземпляров для создания новых структур, которые представляют новые и более сложные объекты. Другим основным недостатком этой схемы является сложность написания алгоритмов расчета свойств изображаемых тел. В алгоритмы должен быть встроен значительный объем информации, специфичной для семейства, и поэтому каждый общий примитив должен рассматриваться как особый случай, не допуская единой общей обработки.

Пространственный учет занятости

Эта схема по сути представляет собой список пространственных ячеек, занятых телом. Ячейки, также называемые вокселами, представляют собой кубы фиксированного размера и расположены в фиксированной пространственной сетке (возможны и другие многогранные расположения, но кубы являются самыми простыми). Каждая ячейка может быть представлена координатами одной точки, например центроида ячейки. Обычно устанавливается определенный порядок сканирования, и соответствующий упорядоченный набор координат называется пространственным массивом . Пространственные массивы представляют собой однозначные и уникальные твердотельные представления, но они слишком многословны для использования в качестве «основных» или определяющих представлений. Однако они могут представлять собой грубые аппроксимации деталей и могут использоваться для повышения производительности геометрических алгоритмов, особенно при использовании в сочетании с другими представлениями, такими как конструктивная твердотельная геометрия .

Разложение клеток

Эта схема следует из комбинаторного (алгебро-топологического) описания твердых тел, подробно описанного выше. Твердое тело можно представить его разложением на несколько ячеек. Схемы пространственного перечисления занятости представляют собой частный случай разложения ячеек, когда все ячейки имеют кубическую форму и лежат в регулярной сетке. Разложение ячеек предоставляет удобные способы вычисления определенных топологических свойств твердых тел, таких как их связность (количество частей) и род (количество дырок). Разложение ячеек в форме триангуляции — это представления, используемые в трехмерных конечных элементах для численного решения уравнений в частных производных. Другие разложения ячеек, такие как регулярная стратификация Уитни или разложение Морса, могут использоваться для приложений при планировании движения робота. ^[6]

Моделирование поверхностной сетки

Подобно представлению границ, отображается поверхность объекта. Однако вместо сложных структур данных и NURBS используется простая поверхностная сетка вершин и ребер. Поверхностные сетки могут быть структурированными (как треугольные сетки в файлах STL или четырехугольные сетки с горизонтальными и вертикальными кольцами четырехугольников) или неструктурированными сетками со случайно сгруппированными треугольниками и многоугольниками более высокого уровня.

Конструктивная сплошная геометрия

Конструктивная твердотельная геометрия (CSG) — это семейство схем представления твердых тел в виде булевых конструкций или комбинаций примитивов с помощью регуляризованных операций над множествами, обсуждавшихся выше. CSG и граничные представления в настоящее время являются наиболее важными схемами представления твердых тел. Представления CSG принимают форму упорядоченных двоичных деревьев , где нетерминальные узлы представляют собой либо жесткие преобразования ( ориентацию сохраняющие изометрии, ), либо регуляризованные операции над множествами. Конечные узлы — это примитивные листья, представляющие замкнутые регулярные множества. Семантика представлений CSG ясна. Каждое поддерево представляет собой набор, полученный в результате применения указанных преобразований/операций регуляризованного множества к множеству, представленному примитивными листьями поддерева. Представления CSG особенно полезны для отражения замысла проекта в виде элементов, соответствующих добавлению или удалению материала (выступы, отверстия, карманы и т. д.). Привлекательные свойства CSG включают краткость, гарантированную достоверность твердых тел, удобные в вычислительном отношении булевы алгебраические свойства и естественный контроль формы твердого тела с точки зрения параметров высокого уровня, определяющих примитивы твердого тела, их положение и ориентацию. Относительно простая структура данных и элегантный рекурсивные алгоритмы ^[7] еще больше способствовали популярности CSG.

Подметание

Основная идея, воплощенная в схемах развертки, проста. Множество, движущееся в пространстве, может отслеживать или сметать объем (твёрдое тело), который может быть представлен движущимся множеством и его траекторией. Такое представление важно в контексте таких приложений, как обнаружение материала, снятого с фрезы при его движении по заданной траектории, вычисление динамического взаимодействия двух твердых тел, испытывающих относительное движение, планирование движения и даже в приложениях компьютерной графики, таких как отслеживание движения кисти, перемещаемой по холсту. Большинство коммерческих САПР предоставляют (ограниченную) функциональность для построения подвижных тел, в основном в виде двумерного поперечного сечения, движущегося по пространственной траектории, поперечной сечению. Однако текущие исследования показали несколько аппроксимаций трехмерных фигур, движущихся по одному параметру, и даже многопараметрических движений.

Неявное представление

Очень общий метод определения набора точек X — указать предикат , который можно вычислить в любой точке пространства. Другими словами, X определяется неявно как состоящий из всех точек, удовлетворяющих условию, заданному предикатом. Простейшей формой предиката является условие на знак действительнозначной функции, приводящее к привычному представлению множеств равенствами и неравенствами. Например, если $f=ax+by+cz+d$ условия $f(p)=0$ , $f(p)>0$ , и $f(p)<0$ представляют собой соответственно плоскость и два открытых линейных полупространства . Более сложные функциональные примитивы могут определяться логическими комбинациями более простых предикатов. Более того, теория R-функций допускает преобразование таких представлений в одно функциональное неравенство для любого замкнутого полуаналитического множества. Такое представление можно преобразовать в граничное представление с помощью алгоритмов полигонизации, например алгоритма марширующих кубов .

Параметрическое и функциональное моделирование

Элементы определяются как параметрические формы, связанные с такими атрибутами , как внутренние геометрические параметры (длина, ширина, глубина и т. д.), положение и ориентация, геометрические допуски , свойства материала и ссылки на другие элементы. ^[8] Функции также обеспечивают доступ к соответствующим производственным процессам и моделям ресурсов. Таким образом, признаки имеют семантически более высокий уровень, чем примитивные замкнутые регулярные множества. Обычно ожидается, что функции станут основой для связи САПР с последующими производственными приложениями, а также для организации баз данных для повторного использования проектных данных. Параметрическое моделирование на основе признаков часто сочетается с конструктивной бинарной твердотельной геометрией (CSG) для полного описания систем сложных объектов в технике.

История твердотельных моделей

Историческое развитие средств твердотельного моделирования следует рассматривать в контексте всей истории САПР , ключевыми вехами которого являются разработка исследовательской системы BUILD, за которой последовало ее коммерческое подразделение Romulus , которое впоследствии повлияло на развитие Parasolid , ACIS и Решения для твердотельного моделирования . Компания АСКОН, один из первых разработчиков САПР в Содружестве Независимых Государств (СНГ), начала внутреннюю разработку собственного твердотельного моделирования в 1990-х годах. ^[9] В ноябре 2012 года математическое подразделение АСКОН выделилось в отдельную компанию и получило название C3D Labs . Была поставлена задача разработать C3D ядро геометрического моделирования как отдельный продукт — единственное коммерческое ядро 3D-моделирования в России. ^[10] Другие вклады поступили от Мянтюля с его GWB и от проекта GPM, который, среди прочего, внес вклад в методы гибридного моделирования в начале 1980-х годов. Именно тогда язык программирования твердотельного моделирования PLaSM в Римском университете был задуман .

Компьютерное проектирование

Моделирование твердых тел — это лишь минимальное требование к возможностям CAD-системы . За последние десять лет твердотельное моделирование стало обычным явлением в инженерных отделах. ^{[ когда? ]} благодаря более быстрым компьютерам и конкурентоспособным ценам на программное обеспечение. Программное обеспечение для твердотельного моделирования создает виртуальное трехмерное представление компонентов для проектирования и анализа машин. ^[11] Типичный графический интерфейс пользователя включает программируемые макросы, сочетания клавиш и манипуляции с динамической моделью. Способность динамически переориентировать модель в трехмерном режиме реального времени подчеркивается и помогает дизайнеру поддерживать мысленный трехмерный образ.

Модель твердотельной детали обычно состоит из группы элементов, добавляемых по одному, пока модель не будет завершена. Инженерные твердотельные модели создаются в основном с использованием функций эскизов; 2-D эскизы, которые перемещаются по траектории и становятся 3-D. Это могут быть, например, разрезы или выдавливания. Работа по проектированию компонентов обычно выполняется в контексте всего продукта с использованием методов моделирования сборки . Модель сборки включает ссылки на модели отдельных деталей, из которых состоит изделие. ^[12]

Другой тип техники моделирования — «поверхностное моделирование» ( Freeform Surface Modeling ). Здесь поверхности определяются, обрезаются, объединяются и заполняются, чтобы сделать их сплошными. Поверхности обычно определяются с помощью базовых кривых в пространстве и множества сложных команд. Наплавка сложнее, но ее лучше применять при некоторых технологиях производства, например при литье под давлением. Твердотельные модели для деталей, отлитых под давлением, обычно имеют функции как для наплавки, так и для эскизов.

Инженерные чертежи могут создаваться полуавтоматически и ссылаться на твердотельные модели.

Параметрическое моделирование

Параметрическое моделирование использует параметры для определения модели (например, размеры). Примерами параметров являются: размеры, используемые для создания элементов модели, плотность материала, формулы для описания элементов по траектории, импортированные данные (например, описывающие опорную поверхность). Параметр может быть изменен позже, и модель обновится, чтобы отразить это изменение. Обычно между деталями, сборками и чертежами существует связь. Деталь состоит из нескольких элементов, а сборка состоит из нескольких частей. Чертежи могут быть выполнены как из деталей, так и из сборок.

Пример: Вал создается путем вытягивания круга диаметром 100 мм. На конце вала установлена ступица. Позже длина вала будет изменена на 200 мм (нажмите на вал, выберите размер длины, измените его на 200). При обновлении модели длина вала составит 200 мм, ступица переместится на конец вала, на котором она была собрана, а все изменения будут автоматически отражены в технических чертежах и массовых характеристиках.

С параметрами связаны, но несколько отличаются ограничения . Ограничения — это отношения между сущностями, которые составляют определенную форму. Для окна стороны могут быть определены как параллельные и одинаковой длины. Параметрическое моделирование очевидно и интуитивно понятно. Но в течение первых трех десятилетий развития САПР это было не так. Модификация означала перерисовку или добавление нового выреза или выступа поверх старых. Размеры на чертежах были созданы , а не показаны . Параметрическое моделирование является очень мощным инструментом, но требует больше навыков в создании моделей. Сложная модель детали, отлитой под давлением, может иметь тысячу функций, и изменение ранней функции может привести к сбою последующих функций. Умело созданные параметрические модели легче поддерживать и модифицировать. Параметрическое моделирование также позволяет повторно использовать данные. целое семейство болтов Например, в одной модели может содержаться .

Медицинское твердотельное моделирование

Современные сканеры компьютерной аксиальной томографии и магнитно-резонансной томографии можно использовать для создания твердотельных моделей внутренних особенностей тела, называемых воксельными моделями, с изображениями, генерируемыми с использованием объемного рендеринга . Оптические 3D-сканеры можно использовать для создания облаков точек или полигональных сетчатых моделей внешних элементов тела.

Использование медицинского твердотельного моделирования;

Визуализация
Визуализация конкретных тканей тела (например, только кровеносных сосудов и опухоли)
Проектирование протезов , ортопедических изделий и других медицинских и стоматологических устройств (иногда это называют массовой кастомизацией )
Создание моделей полигональной сетки для быстрого прототипирования (например, в помощь хирургам при подготовке к сложным операциям)
Объединение моделей полигональной сетки с твердотельным моделированием САПР (например, проектирование запасных частей тазобедренного сустава)
Компьютерный анализ сложных биологических процессов, например, потока воздуха, кровотока.
Компьютерное моделирование новых медицинских изделий и имплантатов in vivo

Если использование выходит за рамки визуализации данных сканирования, такие процессы, как сегментация изображения и создание сетки на основе изображений для создания точного и реалистичного геометрического описания данных сканирования потребуются .

Инженерное дело

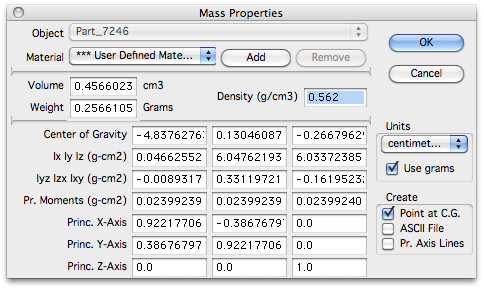
Окно свойств с описанием массовых свойств модели в Cobalt — Окно массовых свойств модели в Cobalt

Поскольку программы САПР, работающие на компьютерах, «понимают» истинную геометрию сложных форм, можно быстро рассчитать многие атрибуты трехмерного твердого тела, такие как его центр тяжести, объем и масса. Например, размер куба с закругленными краями, показанного вверху этой статьи, составляет 8,4 мм от плоскости до плоскости. Несмотря на множество радиусов и неглубокую пирамиду на каждой из шести граней, ее свойства легко рассчитываются дизайнером, как показано на скриншоте справа.

См. также

Каркасное моделирование
Моделирование свободной поверхности
Вычислительная геометрия
Компьютерная графика
Инженерный чертеж
Эйлера Граничное представление
Список компаний CAx
PLaSM – язык программирования твердотельного моделирования.
Технический чертеж

Ссылки

^ Перейти обратно: ^а ^б Шапиро, Вадим (2001). Твердотельное моделирование . Эльзевир . Проверено 20 апреля 2010 г.
^ Рекича, AAG и Фелькер, Х. (1983). «Твердотельное моделирование: современное состояние и направления исследований». IEEE Компьютерная графика и приложения . 3 (7). Компьютерная графика IEEE: 25–37. дои : 10.1109/MCG.1983.263271 . S2CID 14462567 .
^ Тилове, РБ; Рекича, AAG (1980), «Замыкание логических операций над геометрическими объектами», Компьютерное проектирование , 12 (5): 219–220, doi : 10.1016/0010-4485(80)90025-1
^ Перейти обратно: ^а ^б Рекича, AAG (1980). «Представления твердых тел: теория, методы и системы». Обзоры вычислительной техники ACM . 12 (4): 437–464. дои : 10.1145/356827.356833 . S2CID 207568300 .
^ Хэтчер, А. (2002). Алгебраическая топология . Издательство Кембриджского университета . Проверено 20 апреля 2010 г.
^ Кэнни, Джон Ф. (1987). Сложность планирования движения робота . MIT Press, награда за докторскую диссертацию ACM . Проверено 20 апреля 2010 г.
^ Зиглер, М. (2004). «Вычислимые операторы на регулярных множествах». Математическая логика Ежеквартальный журнал . 50 (45). Уайли: 392–404. дои : 10.1002/malq.200310107 . S2CID 17579181 .
^ Мантила М., Нау Д. и Шах Дж. (1996). «Проблемы в производственных исследованиях на основе функций» . Коммуникации АКМ . 39 (2): 77–85. дои : 10.1145/230798.230808 . S2CID 3340804 . {{cite journal}}: CS1 maint: несколько имен: список авторов ( ссылка )
^ Ярес, Эван (апрель 2013 г.). «Русский САПР» . Мир дизайна . 8 (4). ВТВХ Медиа, ООО. ISSN 1941-7217 . Архивировано из оригинала 30 января 2015 года.
^ Голованов, Николай (2014). Геометрическое моделирование: математика форм . Независимая издательская платформа CreateSpace (24 декабря 2014 г.). п. Задняя крышка. ISBN 978-1497473195 .
^ ЛаКурс, Дональд (1995). «2». Справочник по твердотельному моделированию . МакГроу Хилл. п. 2.5. ISBN 978-0-07-035788-4 .
^ ЛаКурс, Дональд (1995). «11». Справочник по твердотельному моделированию . МакГроу Хилл. п. 111.2. ISBN 978-0-07-035788-4 .

Внешние ссылки

[Solid_Modeling-1] Перейти обратно: ^а ^б Шапиро, Вадим (2001). Твердотельное моделирование . Эльзевир . Проверено 20 апреля 2010 г.

[First_Principles-2] Рекича, AAG и Фелькер, Х. (1983). «Твердотельное моделирование: современное состояние и направления исследований». IEEE Компьютерная графика и приложения . 3 (7). Компьютерная графика IEEE: 25–37. дои : 10.1109/MCG.1983.263271 . S2CID 14462567 .

[Regularized_operations-3] Тилове, РБ; Рекича, AAG (1980), «Замыкание логических операций над геометрическими объектами», Компьютерное проектирование , 12 (5): 219–220, doi : 10.1016/0010-4485(80)90025-1

[Representations-4] Перейти обратно: ^а ^б Рекича, AAG (1980). «Представления твердых тел: теория, методы и системы». Обзоры вычислительной техники ACM . 12 (4): 437–464. дои : 10.1145/356827.356833 . S2CID 207568300 .

[Hatcher-5] Хэтчер, А. (2002). Алгебраическая топология . Издательство Кембриджского университета . Проверено 20 апреля 2010 г.

[Complexity_planning-6] Кэнни, Джон Ф. (1987). Сложность планирования движения робота . MIT Press, награда за докторскую диссертацию ACM . Проверено 20 апреля 2010 г.

[Recursivity-7] Зиглер, М. (2004). «Вычислимые операторы на регулярных множествах». Математическая логика Ежеквартальный журнал . 50 (45). Уайли: 392–404. дои : 10.1002/malq.200310107 . S2CID 17579181 .

[Features-8] Мантила М., Нау Д. и Шах Дж. (1996). «Проблемы в производственных исследованиях на основе функций» . Коммуникации АКМ . 39 (2): 77–85. дои : 10.1145/230798.230808 . S2CID 3340804 . {{cite journal}}: CS1 maint: несколько имен: список авторов ( ссылка )

[9] Ярес, Эван (апрель 2013 г.). «Русский САПР» . Мир дизайна . 8 (4). ВТВХ Медиа, ООО. ISSN 1941-7217 . Архивировано из оригинала 30 января 2015 года.

[10] Голованов, Николай (2014). Геометрическое моделирование: математика форм . Независимая издательская платформа CreateSpace (24 декабря 2014 г.). п. Задняя крышка. ISBN 978-1497473195 .

[LaCourse_Handbook-11] ЛаКурс, Дональд (1995). «2». Справочник по твердотельному моделированию . МакГроу Хилл. п. 2.5. ISBN 978-0-07-035788-4 .

[LaCourse_Handbook_11.3-12] ЛаКурс, Дональд (1995). «11». Справочник по твердотельному моделированию . МакГроу Хилл. п. 111.2. ISBN 978-0-07-035788-4 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]