Сферическая тригонометрия

Сферическая тригонометрия — раздел сферической геометрии , изучающий метрические соотношения между сторонами и углами сферических треугольников , традиционно выражаемые с помощью тригонометрических функций . На сфере геодезические большие представляют собой круги . Сферическая тригонометрия имеет большое значение для расчетов в астрономии , геодезии и навигации .

Истоки сферической тригонометрии в греческой математике и основные достижения исламской математики подробно обсуждаются в « Истории тригонометрии и математики в средневековом исламе» . Эта тема получила свое развитие в раннее Новое время благодаря важным разработкам Джона Нэпьера , Деламбра и других и достигла практически завершенной формы к концу девятнадцатого века с публикацией учебника Тодхантера « Сферическая тригонометрия» для использования в колледжах и школах . ^[1]С тех пор значительными достижениями стали применение векторных методов, методов кватернионов и использование численных методов.

Предварительные сведения

Сферические многоугольники

— Сферический многоугольник это многоугольник на поверхности сферы. Его стороны представляют собой дуги больших кругов — сферическая геометрия, эквивалентная отрезкам прямой в плоской геометрии .

Такие многоугольники могут иметь любое количество сторон, превышающее 1. Двусторонние сферические многоугольники — луны , также называемые дигонами или двуугольниками — ограничены двумя дугами большого круга: знакомым примером является изогнутая обращенная наружу поверхность сегмента. апельсина. Три дуги определяют сферический треугольник, основной предмет этой статьи. Аналогичным образом определяются многоугольники с большим числом сторон (4-сторонние сферические четырехугольники, 5-сторонние сферические пятиугольники и т. д.). Аналогично своим плоским аналогам, сферические многоугольники с числом сторон более трех всегда можно рассматривать как композицию сферических треугольников.

Одним из сферических многоугольников с интересными свойствами является pentagramma mirificum , пятисторонний сферический многоугольник со звездой и прямым углом в каждой вершине.

С этого момента в статье обсуждение будет ограничиваться сферическими треугольниками, называемыми просто треугольниками .

Обозначения

и углы при вершинах треугольника обозначаются одинаковыми заглавными буквами $A$ , $B$ и $C.$ И вершины ,
Стороны обозначаются строчными буквами: $a$ , $b$ и $c$ . Радиус сферы равен 1, поэтому длины сторон и строчные углы эквивалентны (см. длину дуги).
Угол , либо, что $A$ (соответственно $B$ и $C$ ) можно рассматривать либо как угол между двумя плоскостями, пересекающими сферу в вершине $A$ то же самое, как угол между касательными дуг большого круга, где они встречаются в вершине A. вершина.
Углы выражаются в радианах . Углы правильных сферических треугольников (по соглашению) меньше $π$ , так что $\pi <A+B+C<3\pi$ (Тодхантер, ^[1] Ст.22,32).

В частности, сумма углов сферического треугольника строго больше суммы углов треугольника, определенного на евклидовой плоскости, которая всегда равна ровно $π$ радиан.

Стороны также выражаются в радианах. Сторона (рассматриваемая как дуга большого круга) измеряется углом, который она образует в центре. На единичной сфере эта радианная мера численно равна длине дуги. По соглашению стороны правильных сферических треугольников меньше $π$ , так что $0<a+b+c<2\pi$ (Тодхантер, ^[1] Ст.22,32).
Радиус сферы принят за единицу. Для конкретных практических задач на сфере радиуса $R$ измеренные длины сторон необходимо разделить на $R,$ прежде чем использовать приведенные ниже тождества. Аналогично, после расчета на единичной сфере стороны $a$ , $b$ и $c$ на $R.$ должны быть умножены

Полярные треугольники

Полярный треугольник , связанный с треугольником $△ ABC,$ определяется следующим образом. Рассмотрим большой круг, содержащий сторону $BC$ . Этот большой круг определяется пересечением диаметральной плоскости с поверхностью. Нарисуйте нормаль к этой плоскости в центре: она пересекает поверхность в двух точках, и точка, которая находится на той же стороне плоскости, что и $A$ , (условно) называется полюсом $A$ и обозначается $A'$ . Точки $B'$ и $C'$ определяются аналогично.

Треугольник $△ A'B'C'$ — это полярный треугольник, соответствующий треугольнику $△ ABC$ . Очень важная теорема (Тодхантер, ^[1] Ст.27) доказывает, что углы и стороны полярного треугольника равныданный ${\begin{alignedat}{3}A'&=\pi -a,&\qquad B'&=\pi -b,&\qquad C'&=\pi -c,\\a'&=\pi -A,&b'&=\pi -B,&c'&=\pi -C.\end{alignedat}}$ Следовательно, если какое-либо тождество доказано для $△ ABC$ , то мы можем немедленно вывести второе тождество, применив первое тождество к полярному треугольнику, сделав указанные выше замены. Вот как дополнительные уравнения косинуса получаются из уравнений косинуса. Точно так же тождества четырехугольного треугольника можно вывести из тождеств прямоугольного треугольника. Полярный треугольник полярного треугольника является исходным треугольником.

Правила косинуса и правила синуса

Косинусные правила

Правило косинуса является фундаментальным тождеством сферической тригонометрии: все остальные тождества, включая правило синуса, могут быть получены из правила косинуса: ${\begin{aligned}\cos a&=\cos b\cos c+\sin b\sin c\cos A,\\[2pt]\cos b&=\cos c\cos a+\sin c\sin a\cos B,\\[2pt]\cos c&=\cos a\cos b+\sin a\sin b\cos C.\end{aligned}}$

Эти тождества обобщают правило косинусов плоской тригонометрии , которому они асимптотически эквивалентны.в пределе малых внутренних углов. (На единичной сфере, если $a,b,c\rightarrow 0$ набор $\sin a\approx a$ и $(\cos a-\cos b)^{2}\approx 0$ и т. д.; см. Сферический закон косинусов .)

Синусоидальные правила

Сферический закон синусов задается формулой ${\frac {\sin A}{\sin a}}={\frac {\sin B}{\sin b}}={\frac {\sin C}{\sin c}}.$ Эти тождества аппроксимируют правило синуса плоской тригонометрии , когда стороны намного меньше радиуса сферы.

Вывод правила косинуса

Формулы сферических косинусов первоначально были доказаны с помощью элементарной геометрии и правила плоского косинуса (Тодхантер, ^[1] ст.37). Он также дает вывод, используя простую геометрию координат и правило плоского косинуса (ст. 60). Описанный здесь подход использует более простые векторные методы. (Эти методы также обсуждаются в разделе «Сферический закон косинусов ».)

Рассмотрим три единичных вектора $OA \to, OB \to, OC \to,$ проведенных из начала координат в вершины треугольника (на единичной сфере). Дуга $BC$ образует угол величины $a$ в центре и, следовательно, $OB \to \cdot OC \to = cos a$ . Введем декартов базис с $OA \to$ вдоль $оси z$ и $OB \to$ в $плоскости xz$ , составляющим угол $c$ с $осью z$ . Вектор $OC \to$ проецируется на $ON$ в $плоскости xy$ угол между $ON$ и $осью x$ равен $A.$ , а Следовательно, три вектора имеют компоненты:

${\begin{aligned}{\vec {OA}}:&\quad (0,\,0,\,1)\\{\vec {OB}}:&\quad (\sin c,\,0,\,\cos c)\\{\vec {OC}}:&\quad (\sin b\cos A,\,\sin b\sin A,\,\cos b).\end{aligned}}$

Скалярное произведение $OB \to \cdot OC \to$ через компоненты равно ${\vec {OB}}\cdot {\vec {OC}}=\sin c\sin b\cos A+\cos c\cos b.$ Приравнивание двух выражений для скалярного произведения дает $\cos a=\cos b\cos c+\sin b\sin c\cos A.$ Это уравнение можно перестроить, чтобы получить явные выражения для угла через стороны: $\cos A={\frac {\cos a-\cos b\cos c}{\sin b\sin c}}.$

Остальные правила косинусов получаются путем циклических перестановок.

Вывод правила синуса

Этот вывод дан в Todhunter, ^[1] (Статья 40). От личности $\sin ^{2}A=1-\cos ^{2}A$ и явное выражение для $cos A,$ данное непосредственно выше ${\begin{aligned}\sin ^{2}A&=1-\left({\frac {\cos a-\cos b\cos c}{\sin b\sin c}}\right)^{2}\\[5pt]&={\frac {(1-\cos ^{2}b)(1-\cos ^{2}c)-(\cos a-\cos b\cos c)^{2}}{\sin ^{2}\!b\,\sin ^{2}\!c}}\\[5pt]{\frac {\sin A}{\sin a}}&={\frac {\sqrt {1-\cos ^{2}\!a-\cos ^{2}\!b-\cos ^{2}\!c+2\cos a\cos b\cos c}}{\sin a\sin b\sin c}}.\end{aligned}}$ Поскольку правая часть инвариантна относительно циклической перестановки $a$ , $b$ и $c,$ немедленно следует правило сферического синуса.

Альтернативные выводы

Существует множество способов вывода фундаментальных правил косинуса и синуса, а также других правил, разработанных в следующих разделах. Например, Тодхантер ^[1] дает два доказательства правила косинуса (статьи 37 и 60) и два доказательства правила синуса (статьи 40 и 42). На странице сферического закона косинусов приведены четыре различных доказательства правила косинусов. Учебники по геодезии ^[2] и сферическая астрономия ^[3] дают разные доказательства, а онлайн-ресурсы MathWorld предоставляют еще больше. ^[4] Есть еще более экзотические варианты, например, Банерджи. ^[5] который выводит формулы, используя линейную алгебру матриц проекций, а также цитирует методы дифференциальной геометрии и групповой теории вращений.

Вывод правила косинуса, представленный выше, имеет преимущества простоты и прямоты, а вывод правила синуса подчеркивает тот факт, что не требуется никакого отдельного доказательства, кроме правила косинуса. Однако приведенная выше геометрия может быть использована для независимого доказательства правила синуса. Скалярное тройное произведение OA $\to \cdot (OB \to \times OC \to)$ оценивается как $sin b sin c sin A$ в показанном базисе. Аналогично, в базисе, ориентированном $z$ вдоль $OB \to$ , тройное произведение $OB \to \cdot (OC \to \times OA \to)$ оценивается как $sin c sin a sin B.$ осью Следовательно, инвариантность тройного произведения относительно циклических перестановок дает $sin b sin A = sin a sin B,$ что является первым из правил синуса. См. изогнутые варианты закона синусов, чтобы увидеть подробности этого вывода.

Личности

Дополнительные правила косинуса

Применение правил косинусов к полярному треугольнику дает (Тодхантер, ^[1] ст.47), т.е. замена $А$ на $π - a$ , $a$ на $π - A$ и т.д., ${\begin{aligned}\cos A&=-\cos B\,\cos C+\sin B\,\sin C\,\cos a,\\\cos B&=-\cos C\,\cos A+\sin C\,\sin A\,\cos b,\\\cos C&=-\cos A\,\cos B+\sin A\,\sin B\,\cos c.\end{aligned}}$

Котангенсные четырехчастные формулы

Шесть частей треугольника можно записать в циклическом порядке как ( $aCbAcB$ ). Формулы котангенса, или четырехчастных, связывают две стороны и два угла, образующие четыре последовательные части вокруг треугольника, например ( $aCbA$ ) или $BaCb$ ). В таком наборе есть внутренняя и внешняя части: например в наборе ( $BaCb$ ) внутренний угол — $C$ , внутренняя сторона — $a$ , внешний угол — $B$ , внешняя сторона — $b$ . Правило котангенса можно записать как (Тодхантер, ^[1] Ст.44) $\cos \!{\Bigl (}{\begin{smallmatrix}{\text{inner}}\\{\text{side}}\end{smallmatrix}}{\Bigr )}\cos \!{\Bigl (}{\begin{smallmatrix}{\text{inner}}\\{\text{angle}}\end{smallmatrix}}{\Bigr )}=\cot \!{\Bigl (}{\begin{smallmatrix}{\text{outer}}\\{\text{side}}\end{smallmatrix}}{\Bigr )}\sin \!{\Bigl (}{\begin{smallmatrix}{\text{inner}}\\{\text{side}}\end{smallmatrix}}{\Bigr )}-\cot \!{\Bigl (}{\begin{smallmatrix}{\text{outer}}\\{\text{angle}}\end{smallmatrix}}{\Bigr )}\sin \!{\Bigl (}{\begin{smallmatrix}{\text{inner}}\\{\text{angle}}\end{smallmatrix}}{\Bigr )},$ и шесть возможных уравнений (соответствующий набор показан справа): ${\begin{alignedat}{5}{\text{(CT1)}}&&\qquad \cos b\,\cos C&=\cot a\,\sin b-\cot A\,\sin C\qquad &&(aCbA)\\[0ex]{\text{(CT2)}}&&\cos b\,\cos A&=\cot c\,\sin b-\cot C\,\sin A&&(CbAc)\\[0ex]{\text{(CT3)}}&&\cos c\,\cos A&=\cot b\,\sin c-\cot B\,\sin A&&(bAcB)\\[0ex]{\text{(CT4)}}&&\cos c\,\cos B&=\cot a\,\sin c-\cot A\,\sin B&&(AcBa)\\[0ex]{\text{(CT5)}}&&\cos a\,\cos B&=\cot c\,\sin a-\cot C\,\sin B&&(cBaC)\\[0ex]{\text{(CT6)}}&&\cos a\,\cos C&=\cot b\,\sin a-\cot B\,\sin C&&(BaCb)\end{alignedat}}$ Чтобы доказать первую формулу, начните с первого правила косинуса и в правой части замените $cos c$ из третьего правила косинуса: ${\begin{aligned}\cos a&=\cos b\cos c+\sin b\sin c\cos A\\&=\cos b\ (\cos a\cos b+\sin a\sin b\cos C)+\sin b\sin C\sin a\cot A\\\cos a\sin ^{2}b&=\cos b\sin a\sin b\cos C+\sin b\sin C\sin a\cot A.\end{aligned}}$ Результат получается после деления на $sin a sin b$ . Подобные методыа два других правила косинуса дают CT3 и CT5. Остальные три уравнения получаются путем применения правил 1, 3 и 5 к полярному треугольнику.

Формулы половинного угла и полустороны

С $2s=(a+b+c)$ и $2S=(A+B+C),$ ${\begin{alignedat}{5}\sin {\tfrac {1}{2}}A&={\sqrt {\frac {\sin(s-b)\sin(s-c)}{\sin b\sin c}}}&\qquad \qquad \sin {\tfrac {1}{2}}a&={\sqrt {\frac {-\cos S\cos(S-A)}{\sin B\sin C}}}\\[2ex]\cos {\tfrac {1}{2}}A&={\sqrt {\frac {\sin s\sin(s-a)}{\sin b\sin c}}}&\cos {\tfrac {1}{2}}a&={\sqrt {\frac {\cos(S-B)\cos(S-C)}{\sin B\sin C}}}\\[2ex]\tan {\tfrac {1}{2}}A&={\sqrt {\frac {\sin(s-b)\sin(s-c)}{\sin s\sin(s-a)}}}&\tan {\tfrac {1}{2}}a&={\sqrt {\frac {-\cos S\cos(S-A)}{\cos(S-B)\cos(S-C)}}}\end{alignedat}}$

Еще двенадцать тождеств следуют циклической перестановке.

Доказательство (Тодхантер, ^[1] ст.49) первой формулы исходит из тождества $2\sin ^{2}\!{\tfrac {A}{2}}=1-\cos A,$ используя правило косинусов, чтобы выразить $A$ через стороны и заменяя сумму двух косинусов произведением. (См. тождества суммы и произведения .) Вторая формула начинается с тождества $2\cos ^{2}\!{\tfrac {A}{2}}=1+\cos A,$ третье является частным, а остаток получается путем применения результатов к полярному треугольнику.

Ветхие аналогии

Аналогии Деламбра (также называемые аналогиями Гаусса) были опубликованы независимо Деламбром, Гауссом и Молвейде в 1807–1809 годах. ^[6]

${\begin{aligned}{\frac {\sin {\tfrac {1}{2}}(A+B)}{\cos {\tfrac {1}{2}}C}}={\frac {\cos {\tfrac {1}{2}}(a-b)}{\cos {\tfrac {1}{2}}c}}&\qquad \qquad &{\frac {\sin {\tfrac {1}{2}}(A-B)}{\cos {\tfrac {1}{2}}C}}={\frac {\sin {\tfrac {1}{2}}(a-b)}{\sin {\tfrac {1}{2}}c}}\\[2ex]{\frac {\cos {\tfrac {1}{2}}(A+B)}{\sin {\tfrac {1}{2}}C}}={\frac {\cos {\tfrac {1}{2}}(a+b)}{\cos {\tfrac {1}{2}}c}}&\qquad &{\frac {\cos {\tfrac {1}{2}}(A-B)}{\sin {\tfrac {1}{2}}C}}={\frac {\sin {\tfrac {1}{2}}(a+b)}{\sin {\tfrac {1}{2}}c}}\end{aligned}}$ Еще восемь тождеств следуют циклической перестановке.

Доказано путем разложения числителей и использования формул половинного угла. (Тодхантер, ^[1] Статья 54 и Деламбре ^[7])

Аналогии Нейпира

${\begin{aligned}\tan {\tfrac {1}{2}}(A+B)={\frac {\cos {\tfrac {1}{2}}(a-b)}{\cos {\tfrac {1}{2}}(a+b)}}\cot {\tfrac {1}{2}}C&\qquad &\tan {\tfrac {1}{2}}(a+b)={\frac {\cos {\tfrac {1}{2}}(A-B)}{\cos {\tfrac {1}{2}}(A+B)}}\tan {\tfrac {1}{2}}c\\[2ex]\tan {\tfrac {1}{2}}(A-B)={\frac {\sin {\tfrac {1}{2}}(a-b)}{\sin {\tfrac {1}{2}}(a+b)}}\cot {\tfrac {1}{2}}C&\qquad &\tan {\tfrac {1}{2}}(a-b)={\frac {\sin {\tfrac {1}{2}}(A-B)}{\sin {\tfrac {1}{2}}(A+B)}}\tan {\tfrac {1}{2}}c\end{aligned}}$

Еще восемь тождеств следуют циклической перестановке.

Эти тождества следуют делением формул Деламбра. (Тодхантер, ^[1] Ст.52)

Взяв частное из них, получим закон тангенса , впервые сформулированный персидским математиком Насир ад-Дином ат-Туси (1201–1274):

${\frac {\tan {\tfrac {1}{2}}(A-B)}{\tan {\tfrac {1}{2}}(A+B)}}={\frac {\tan {\tfrac {1}{2}}(a-b)}{\tan {\tfrac {1}{2}}(a+b)}}$

Правила Непера для прямоугольных сферических треугольников.

Когда один из углов сферического треугольника, скажем, $C$ , равен $π$ /2, различные приведенные выше тождества значительно упрощаются. Существует десять тождеств, связывающих три элемента, выбранных из $a$ , $b$ , $c$ , $A$ и $B.$ множества

Нэпьер ^[8] предоставил элегантную мнемоническую помощь для десяти независимых уравнений: мнемоника называется кругом Непера или пятиугольником Непира (когда круг на рисунке выше справа заменяется пятиугольником).

Сначала напишите шесть частей треугольника (три угла при вершине, три угла дуги для сторон) в том порядке, в котором они встречаются вокруг любого контура треугольника: для треугольника, показанного выше слева, движение по часовой стрелке, начиная с $a$ , дает $aCbAcB$ . Затем замените части, не примыкающие к $C$ (то есть $A$ , $c$ и $B$ ), их дополнениями, а затем удалите угол $C$ из списка. Остальные части можно затем нарисовать в виде пяти упорядоченных равных частей пентаграммы или круга, как показано на рисунке выше (справа). При любом выборе трех смежных частей одна ( средняя часть) будет примыкать к двум частям и находиться напротив двух других частей. Десять правил Нейпира сформулированы следующим образом:

синус средней части = произведение тангенсов соседних частей
синус средней части = произведение косинусов противоположных частей

Чтобы запомнить, какая тригонометрическая функция с какой частью связана, нужно посмотреть на первую гласную вида части: средние части берут синус, соседние части - тангенс, а противоположные части - косинус.Например, начиная с сектора, содержащего $a,$ мы имеем: ${\begin{aligned}\sin a&=\tan({\tfrac {\pi }{2}}-B)\,\tan b\\[2pt]&=\cos({\tfrac {\pi }{2}}-c)\,\cos({\tfrac {\pi }{2}}-A)\\[2pt]&=\cot B\,\tan b\\[4pt]&=\sin c\,\sin A.\end{aligned}}$ Полный набор правил для правильного сферического треугольника (Тодхантер, ^[1] Ст.62) ${\begin{alignedat}{4}&{\text{(R1)}}&\qquad \cos c&=\cos a\,\cos b,&\qquad \qquad &{\text{(R6)}}&\qquad \tan b&=\cos A\,\tan c,\\&{\text{(R2)}}&\sin a&=\sin A\,\sin c,&&{\text{(R7)}}&\tan a&=\cos B\,\tan c,\\&{\text{(R3)}}&\sin b&=\sin B\,\sin c,&&{\text{(R8)}}&\cos A&=\sin B\,\cos a,\\&{\text{(R4)}}&\tan a&=\tan A\,\sin b,&&{\text{(R9)}}&\cos B&=\sin A\,\cos b,\\&{\text{(R5)}}&\tan b&=\tan B\,\sin a,&&{\text{(R10)}}&\cos c&=\cot A\,\cot B.\end{alignedat}}$

Правила Непера для четырехугольных треугольников.

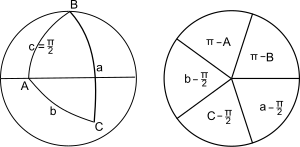
Квадрантный сферический треугольник определяется как сферический треугольник, в котором одна из сторон образует угол в $π$ /2 радиан в центре сферы: на единичной сфере сторона имеет длину $π$ /2. В случае, когда сторона $c$ имеет длину $π$ /2 на единичной сфере, уравнения, определяющие остальные стороны и углы, можно получить, применив правила для прямоугольного сферического треугольника из предыдущего раздела к полярному треугольнику $△ A'B'C '$ со сторонами $a', b', c'$ такими, что $A' = π - a$ , $a' = π - A$ и т. д. Результаты: ${\begin{alignedat}{4}&{\text{(Q1)}}&\qquad \cos C&=-\cos A\,\cos B,&\qquad \qquad &{\text{(Q6)}}&\qquad \tan B&=-\cos a\,\tan C,\\&{\text{(Q2)}}&\sin A&=\sin a\,\sin C,&&{\text{(Q7)}}&\tan A&=-\cos b\,\tan C,\\&{\text{(Q3)}}&\sin B&=\sin b\,\sin C,&&{\text{(Q8)}}&\cos a&=\sin b\,\cos A,\\&{\text{(Q4)}}&\tan A&=\tan a\,\sin B,&&{\text{(Q9)}}&\cos b&=\sin a\,\cos B,\\&{\text{(Q5)}}&\tan B&=\tan b\,\sin A,&&{\text{(Q10)}}&\cos C&=-\cot a\,\cot b.\end{alignedat}}$

Правила из пяти частей

Подстановка второго правила косинусов в первое и упрощение дает: ${\begin{aligned}\cos a&=(\cos a\,\cos c+\sin a\,\sin c\,\cos B)\cos c+\sin b\,\sin c\,\cos A\\[4pt]\cos a\,\sin ^{2}c&=\sin a\,\cos c\,\sin c\,\cos B+\sin b\,\sin c\,\cos A\end{aligned}}$ Отмена фактора $sin c$ дает $\cos a\sin c=\sin a\,\cos c\,\cos B+\sin b\,\cos A$

Подобные замены в других формулах косинуса и дополнительных косинусов дают большое разнообразие правил из 5 частей. Они используются редко.

Уравнение Каньоли

Умножение первого правила косинусов на $cos A$ дает $\cos a\cos A=\cos b\,\cos c\,\cos A+\sin b\,\sin c-\sin b\,\sin c\,\sin ^{2}A.$ Аналогично, умножив первое правило дополнительных косинусов на $cos a,$ получим $\cos a\cos A=-\cos B\,\cos C\,\cos a+\sin B\,\sin C-\sin B\,\sin C\,\sin ^{2}a.$ Вычитая два и отмечая, что из правил синуса следует, что $\sin b\,\sin c\,\sin ^{2}A=\sin B\,\sin C\,\sin ^{2}a$ дает уравнение Каньоли $\sin b\,\sin c+\cos b\,\cos c\,\cos A=\sin B\,\sin C-\cos B\,\cos C\,\cos a$ которое представляет собой соотношение между шестью частями сферического треугольника. ^[9]

Решение треугольников

Косые треугольники

Решение треугольников — основная цель сферической тригонометрии: по трем, четырем или пяти элементам треугольника определить остальные. Случай пяти заданных элементов тривиален и требует лишь однократного применения правила синуса. Для четырех заданных элементов существует один нетривиальный случай, который обсуждается ниже. Для трех данных элементов имеется шесть случаев: три стороны, две стороны и заключённый или противолежащий угол, два угла и заключённая или противолежащая сторона, или три угла. (Последний случай не имеет аналога в плоской тригонометрии.) Ни один метод не решает все случаи. На рисунке ниже показаны семь нетривиальных случаев: в каждом случае заданные стороны отмечены перекладиной, а заданные углы - дугой. (Данные элементы также указаны под треугольником). В сводных обозначениях здесь, таких как ASA, A относится к данному углу, а S относится к данной стороне, а последовательность букв A и S в обозначениях относится к соответствующей последовательности в треугольнике.

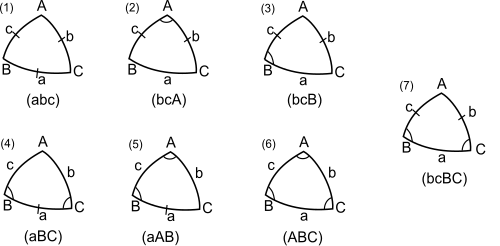
Случай 1: даны три стороны (SSS). Для определения углов $A$ , $B$ и $C$ можно использовать правило косинуса , но, чтобы избежать двусмысленности, предпочтительны формулы половинного угла.
Случай 2: заданы две стороны и прилежащий угол (SAS). Правило косинуса дает $a$ , и тогда мы возвращаемся к случаю 1.
Случай 3: даны две стороны и противоположный угол (SSA). Правило синуса дает $C$ , и тогда мы имеем случай 7. Существует либо одно, либо два решения.
Случай 4: даны два угла и включенная сторона (ASA). Четырехчастные формулы котангенса для множеств ( $cBaC$ ) и ( $BaCb$ ) дают $c$ и $b$ , тогда $A$ следует из правила синуса.
Случай 5: даны два угла и противолежащая сторона (ААС). Правило синуса дает $b$ , и тогда мы имеем случай 7 (повернутый). Есть одно или два решения.
Случай 6: даны три угла (ААА). Для определения сторон $a$ , $b$ и $c$ можно использовать правило дополнительного косинуса , но, чтобы избежать двусмысленности, предпочтительнее использовать формулы полусторон.
Случай 7: даны два угла и две противоположные стороны (SSAA). Используйте аналогии Нейпира для $a$ и $A$ ; или используйте вариант 3 (SSA) или вариант 5 (AAS).

Перечисленные здесь методы решения не являются единственно возможными вариантами: возможны многие другие. В общем, лучше выбирать методы, которые избегают использования обратного синуса из-за возможной неоднозначности между углом и его дополнением. Использование формул половинного угла часто целесообразно, поскольку половинные углы будут меньше $π$ /2 и, следовательно, не будут двусмысленными. В Тодхантере есть полное обсуждение. В статье Решение треугольников # Решение сферических треугольников представлены варианты этих методов с немного другими обозначениями.

В Тодхантере есть полное обсуждение решения косоугольных треугольников. ^[1]^{: Гл. МЫ} См. также обсуждение в Росс. ^[10] Насир ад-Дин ат-Туси был первым, кто перечислил шесть различных случаев (2–7 на диаграмме) прямоугольного треугольника в сферической тригонометрии. ^[11]

Решение прямоугольными треугольниками

Другой подход — разделить треугольник на два прямоугольных треугольника. Например, возьмем пример случая 3, где $b$ , $c$ и $B.$ заданы Постройте большой круг из $точки A$ перпендикулярной стороне $BC$ в точке $D.$ , Используйте правила Нейпира, чтобы решить треугольник $△ ABD$ : используйте $c$ и $B,$ чтобы найти стороны $AD$ и $BD$ и угол $∠ BAD$ . Затем используйте правила Нейпира, чтобы решить треугольник $△ ACD$ : то есть используйте $AD$ и $b$ , чтобы найти сторону $DC$ и углы $C$ и $∠ DAC$ . Угол $А$ и сторона $а$ следуют сложением.

Численные соображения

Не все полученные правила являются численно устойчивыми в крайних примерах, например, когда угол приближается к нулю или $π$ . Проблемы и решения, возможно, придется тщательно изучить, особенно при написании кода для решения произвольного треугольника.

Площадь и сферический избыток

Рассмотрим $N$ -сторонний сферический многоугольник и $An n$ обозначим через $-й$ внутренний угол. Площадь такого многоугольника определяется выражением (Todhunter, ^[1] Ст.99) ${{\text{Area of polygon}} \atop {\text{(on the unit sphere)}}}\equiv E_{N}=\left(\sum _{n=1}^{N}A_{n}\right)-(N-2)\pi .$

Для случая сферического треугольника с углами $A$ , $B$ и $C$ это сводится к теореме Жирара. ${{\text{Area of triangle}} \atop {\text{(on the unit sphere)}}}\equiv E=E_{3}=A+B+C-\pi ,$ где $E$ — величина, на которую сумма углов превышает $π$ радиан, называемая сферическим избытком треугольника. Эта теорема названа в честь ее автора Альбера Жирара . ^[12] Более раннее доказательство было получено, но не опубликовано английским математиком Томасом Хэрриотом . На сфере радиуса $R$ оба приведенных выше выражения площади умножаются на $R 2$ . Определение избытка не зависит от радиуса сферы.

Обратный результат можно записать как

$A+B+C=\pi +{\frac {4\pi \times {\text{Area of triangle}}}{\text{Area of the sphere}}}.$

Поскольку площадь треугольника не может быть отрицательной, сферический избыток всегда положителен. Оно не обязательно мало, поскольку сумма углов может достигать 5 $π$ (3 $π$ для собственных углов). Например,октант сферы — это сферический треугольник с тремя прямыми углами, так что избыток равен $π$ /2. В практических приложениях он часто невелик: например, треугольники геодезических съемок обычно имеют сферический избыток, составляющий намного меньше 1 фута дуги. ^[13] На Земле превышение равностороннего треугольника со сторонами 21,3 км (и площадью 393 км ²) составляет примерно 1 угловую секунду.

Существует множество формул для избытка. Например, Тодхантер, ^[1] (Статьи 101–103) приводят десять примеров, включая пример Л'Юилье : $\tan {\tfrac {1}{4}}E={\sqrt {\tan {\tfrac {1}{2}}s\,\tan {\tfrac {1}{2}}(s-a)\,\tan {\tfrac {1}{2}}(s-b)\,\tan {\tfrac {1}{2}}(s-c)}}$ где $s={\tfrac {1}{2}}(a+b+c)$

Поскольку некоторые треугольники плохо характеризуютсяих края (например, если ${\textstyle a=b\approx {\frac {1}{2}}c}$ ), часто лучше использоватьформула превышения через два ребра и прилежащий к ним угол $\tan {\tfrac {1}{2}}E={\frac {\tan {\frac {1}{2}}a\tan {\frac {1}{2}}b\sin C}{1+\tan {\frac {1}{2}}a\tan {\frac {1}{2}}b\cos C}}.$

Когда треугольник $△ ABC$ — прямоугольный треугольник с прямым углом в $C$ , тогда $cos C = 0$ и $sin C = 1$ , поэтому это сводится к $\tan {\tfrac {1}{2}}E=\tan {\tfrac {1}{2}}a\tan {\tfrac {1}{2}}b.$

Дефицит угла определяется аналогично для гиперболической геометрии .

От широты и долготы

Сферический избыток сферического четырехугольника, ограниченного экватором, двумя меридианами долгот. $\lambda _{1}$ и $\lambda _{2},$ и дуга большого круга между двумя точками с долготой и широтой $(\lambda _{1},\varphi _{1})$ и $(\lambda _{2},\varphi _{2})$ является $\tan {\tfrac {1}{2}}E_{4}={\frac {\sin {\tfrac {1}{2}}(\varphi _{2}+\varphi _{1})}{\cos {\tfrac {1}{2}}(\varphi _{2}-\varphi _{1})}}\tan {\tfrac {1}{2}}(\lambda _{2}-\lambda _{1}).$

Этот результат получен на основе одной из аналогий Непера. В пределе, где $\varphi _{1},\varphi _{2},\lambda _{2}-\lambda _{1}$ все маленькие, это сводится к привычной трапециевидной области, ${\textstyle E_{4}\approx {\frac {1}{2}}(\varphi _{2}+\varphi _{1})(\lambda _{2}-\lambda _{1})}$ .

Площадь многоугольника можно вычислить по отдельным четырехугольникам указанного выше типа, по (аналогично) отдельному треугольнику, ограниченному отрезком многоугольника и двумя меридианами, ^[14] линейным интегралом по теореме Грина , ^[15] или с помощью равновеликой проекции , как это обычно делается в ГИС. Другие алгоритмы по-прежнему можно использовать с длинами сторон, рассчитанными по формуле расстояния по большому кругу .

См. также

Ссылки

^ Перейти обратно: ^а ^б ^с ^д ^и ^ж ^г ^час ^я ^дж ^к ^л ^м ^н ^тот ^п Тодхантер, И. (1886). Сферическая тригонометрия (5-е изд.). Макмиллан. Архивировано из оригинала 14 апреля 2020 г. Проверено 28 июля 2013 г.
^ Кларк, Александр Росс (1880). Геодезия . Оксфорд: Кларендон Пресс. OCLC 2484948 — через Интернет-архив .
^ Смарт, WM (1977). Учебник по сферической астрономии (6-е изд.). Издательство Кембриджского университета. Глава 1 – через Интернет-архив .
^ Вайсштейн, Эрик В. «Сферическая тригонометрия» . Математический мир . Проверено 8 апреля 2018 г.
^ Банерджи, Судипто (2004), «Возвращаясь к сферической тригонометрии с ортогональными проекторами» , The College Mathematics Journal , 35 (5), Mathematical Association of America: 375–381, doi : 10.1080/07468342.2004.11922099 , JSTOR 4146847 , ID 122277398 , в архиве из оригинала от 22 июля 2020 г. , получено 10 января 2016 г.
^ Тодхантер, Исаак (1873). «Заметка об истории некоторых формул сферической тригонометрии». Лондонский, Эдинбургский и Дублинский философский журнал и научный журнал . 45 (298): 98–100. дои : 10.1080/14786447308640820 .
^ Деламбре, JBJ (1807). Connaissance des Temps 1809 . п. 445. Архивировано из оригинала 22 июля 2020 г. Проверено 14 мая 2016 г.
^ Нэпьер, Дж (1614). Мирифичи Логарифморум Канонис Конструкцио . п. 50. Архивировано из оригинала 30 апреля 2013 г. Проверено 14 мая 2016 г. Перевод 1889 года «Построение чудесного канона логарифмов» доступен в виде электронной книги в Abe Books, заархивировано 3 марта 2020 г. на Wayback Machine.
^ Шовене, Уильям (1867). Трактат о плоской и сферической тригонометрии . Филадельфия: JB Lippincott & Co. 165. Архивировано из оригинала 11 июля 2021 г. Проверено 11 июля 2021 г.
^ Росс, Дебра Энн. Магистр математики: тригонометрия , Career Press, 2002.
^ О'Коннор, Джон Дж.; Робертсон, Эдмунд Ф. , «Насир ад-Дин аль-Туси» , Архив истории математики MacTutor , Университет Сент-Эндрюса «Одним из наиболее важных математических вкладов аль-Туси было создание тригонометрии как самостоятельной математической дисциплины, а не чем просто инструмент для астрономических приложений. В «Трактате о четырехугольнике» ат-Туси дал первое дошедшее до нас изложение всей системы плоской и сферической тригонометрии. Эта работа действительно является первой в истории тригонометрией как самостоятельной отраслью чистой математики. первый, в котором изложены все шесть случаев прямоугольного сферического треугольника»
^ Еще одно доказательство теоремы Жирара можно найти по адресу [1]. Архивировано 31 октября 2012 г. в Wayback Machine .
^ Это следует из теоремы Лежандра о сферических треугольниках , когда площадь треугольника мала по сравнению с площадью поверхности всей Земли; видеть Кларк, Александр Росс (1880). Геодезия . Кларендон Пресс. (главы 2 и 9).
^ Чемберлен, Роберт Г.; Дюкетт, Уильям Х. (17 апреля 2007 г.). Некоторые алгоритмы для многоугольников на сфере . Ежегодное собрание Ассоциации американских географов. Лаборатория реактивного движения НАСА. Архивировано из оригинала 22 июля 2020 года . Проверено 7 августа 2020 г.
^ «Площадь многоугольника на сфере или эллипсоиде – MATLAB areaint» . www.mathworks.com . Архивировано из оригинала 1 мая 2021 г. Проверено 1 мая 2021 г.

Внешние ссылки

Вайсштейн, Эрик В. «Сферическая тригонометрия» . Математический мир . более подробный список личностей с некоторыми выводами
Вайсштейн, Эрик В. «Сферический треугольник» . Математический мир . более подробный список личностей с некоторыми выводами
TriSph Бесплатное программное обеспечение для решения сферических треугольников, настраиваемое для различных практических приложений и настроенное для гномонических вычислений.
«Возвращаясь к сферической тригонометрии с помощью ортогональных проекторов» Судипто Банерджи. В статье выводятся сферический закон косинусов и закон синусов с использованием элементарной линейной алгебры и матриц проекций.
«Наглядное доказательство теоремы Жирара» . Демонстрационный проект Wolfram . от Окей Арик
«Книга инструкций по отклонениям и простым плоскостям» , рукопись на арабском языке, датируемая 1740 годом и рассказывающая о сферической тригонометрии, с диаграммами.
Некоторые алгоритмы для многоугольников на сфере Роберт Г. Чемберлен, Уильям Х. Дюкетт, Лаборатория реактивного движения. В статье развиваются и объясняются многие полезные формулы, возможно, с упором на навигацию и картографию.
Онлайн расчет сферических треугольников

[todhunter-1] Перейти обратно: ^а ^б ^с ^д ^и ^ж ^г ^час ^я ^дж ^к ^л ^м ^н ^тот ^п Тодхантер, И. (1886). Сферическая тригонометрия (5-е изд.). Макмиллан. Архивировано из оригинала 14 апреля 2020 г. Проверено 28 июля 2013 г.

[2] Кларк, Александр Росс (1880). Геодезия . Оксфорд: Кларендон Пресс. OCLC 2484948 — через Интернет-архив .

[3] Смарт, WM (1977). Учебник по сферической астрономии (6-е изд.). Издательство Кембриджского университета. Глава 1 – через Интернет-архив .

[4] Вайсштейн, Эрик В. «Сферическая тригонометрия» . Математический мир . Проверено 8 апреля 2018 г.

[banerjee-5] Банерджи, Судипто (2004), «Возвращаясь к сферической тригонометрии с ортогональными проекторами» , The College Mathematics Journal , 35 (5), Mathematical Association of America: 375–381, doi : 10.1080/07468342.2004.11922099 , JSTOR 4146847 , ID 122277398 , в архиве из оригинала от 22 июля 2020 г. , получено 10 января 2016 г.

[6] Тодхантер, Исаак (1873). «Заметка об истории некоторых формул сферической тригонометрии». Лондонский, Эдинбургский и Дублинский философский журнал и научный журнал . 45 (298): 98–100. дои : 10.1080/14786447308640820 .

[7] Деламбре, JBJ (1807). Connaissance des Temps 1809 . п. 445. Архивировано из оригинала 22 июля 2020 г. Проверено 14 мая 2016 г.

[8] Нэпьер, Дж (1614). Мирифичи Логарифморум Канонис Конструкцио . п. 50. Архивировано из оригинала 30 апреля 2013 г. Проверено 14 мая 2016 г. Перевод 1889 года «Построение чудесного канона логарифмов» доступен в виде электронной книги в Abe Books, заархивировано 3 марта 2020 г. на Wayback Machine.

[9] Шовене, Уильям (1867). Трактат о плоской и сферической тригонометрии . Филадельфия: JB Lippincott & Co. 165. Архивировано из оригинала 11 июля 2021 г. Проверено 11 июля 2021 г.

[10] Росс, Дебра Энн. Магистр математики: тригонометрия , Career Press, 2002.

[11] О'Коннор, Джон Дж.; Робертсон, Эдмунд Ф. , «Насир ад-Дин аль-Туси» , Архив истории математики MacTutor , Университет Сент-Эндрюса «Одним из наиболее важных математических вкладов аль-Туси было создание тригонометрии как самостоятельной математической дисциплины, а не чем просто инструмент для астрономических приложений. В «Трактате о четырехугольнике» ат-Туси дал первое дошедшее до нас изложение всей системы плоской и сферической тригонометрии. Эта работа действительно является первой в истории тригонометрией как самостоятельной отраслью чистой математики. первый, в котором изложены все шесть случаев прямоугольного сферического треугольника»

[12] Еще одно доказательство теоремы Жирара можно найти по адресу [1]. Архивировано 31 октября 2012 г. в Wayback Machine .

[clarke-13] Это следует из теоремы Лежандра о сферических треугольниках , когда площадь треугольника мала по сравнению с площадью поверхности всей Земли; видеть Кларк, Александр Росс (1880). Геодезия . Кларендон Пресс. (главы 2 и 9).

[14] Чемберлен, Роберт Г.; Дюкетт, Уильям Х. (17 апреля 2007 г.). Некоторые алгоритмы для многоугольников на сфере . Ежегодное собрание Ассоциации американских географов. Лаборатория реактивного движения НАСА. Архивировано из оригинала 22 июля 2020 года . Проверено 7 августа 2020 г.

[15] «Площадь многоугольника на сфере или эллипсоиде – MATLAB areaint» . www.mathworks.com . Архивировано из оригинала 1 мая 2021 г. Проверено 1 мая 2021 г.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]