Правило фаз

«Правило Гиббса» перенаправляется сюда. Не путать с делом « Энтони Гиббс и сыновья против La Societe Industrielle et Commerciale des Metaux» .

В термодинамике правило фаз — это общий принцип, управляющий системами «pVT», термодинамические состояния которых полностью описываются переменными давлением ( p ), объемом ( V ) и температурой ( T ) в термодинамическом равновесии . Если F — количество степеней свободы , C — количество компонентов , а P — количество фаз , то

$F=C-P+2$

Его вывел американский физик Джозайя Уиллард Гиббс в своей знаковой статье « О равновесии гетерогенных веществ» , опубликованной частями между 1875 и 1878 годами. Правило предполагает, что компоненты не вступают в реакцию друг с другом.

Число степеней свободы — это количество независимых интенсивных переменных , т. е. наибольшее число термодинамических параметров, таких как температура или давление, которые можно изменять одновременно и произвольно, не определяя друг друга. Примером однокомпонентной системы является система, включающая одно чистое химическое вещество, тогда как двухкомпонентные системы, такие как смеси воды и этанола, имеют два химически независимых компонента и так далее. Типичными фазами являются твердые тела , жидкости и газы .

Фундаменты

• Фаза — это форма вещества, однородная по химическому составу и физическому состоянию . Типичными фазами являются твердая, жидкая и газообразная. Две несмешивающиеся жидкости (или смеси жидкостей разного состава), разделенные четкой границей, считаются двумя разными фазами, как и два несмешивающихся твердых вещества.
• Число компонентов ( C ) — это количество химически независимых составляющих системы, т.е. минимальное количество независимых частиц, необходимое для определения состава всех фаз системы.
  Примеры см. в компоненте (термодинамика) .
• Число степеней свободы ( F ) в данном контексте — это количество интенсивных переменных, независимых друг от друга.

Основа правила заключается в том, что равновесие между фазами накладывает ограничения на интенсивные переменные. Более строго, поскольку фазы находятся в термодинамическом равновесии друг с другом, химические потенциалы фаз должны быть равны. Количество отношений равенства определяет количество степеней свободы. Например, если химические потенциалы жидкости и ее пара зависят от температуры ( Т ) и давления ( р ), равенство химических потенциалов будет означать, что каждая из этих переменных будет зависеть от другой. Математически уравнение μ _liq ( T , p ) = μ _vap ( T , p ) , где μ , химический потенциал, определяет температуру как функцию давления или наоборот. (Внимание: не путайте p как давление с P как количество фаз.)

Более конкретно, состав каждой фазы определяется C - 1 интенсивными переменными (такими как мольные доли) в каждой фазе. Общее количество переменных равно ( C − 1) P + 2 , где дополнительные две — это температура T и давление p . Количество ограничений равно C ( P − 1) , поскольку химический потенциал каждого компонента должен быть одинаковым во всех фазах. Вычтите количество ограничений из количества переменных, чтобы получить количество степеней свободы как F = ( C - 1) P + 2 - C ( P - 1) = C - P + 2 .

Правило справедливо при условии, что на равновесие между фазами не влияют гравитационные, электрические или магнитные силы или площадь поверхности, а только температура, давление и концентрация.

Последствия и примеры

Чистые вещества (один компонент)

Для чистых веществ C = 1, так что F = 3 − P . В однофазном ( P = 1 ) состоянии чистой компонентной системы две переменные ( F = 2 ), такие как температура и давление, могут быть выбраны независимо и представлять собой любую пару значений, соответствующих фазе. Однако если сочетание температуры и давления доходит до точки, где чистый компонент подвергается разделению на две фазы ( P = 2 ), F уменьшается с 2 до 1. Когда система переходит в двухфазную область, это становится невозможным. самостоятельно контролировать температуру и давление.

Фазовая диаграмма давления и температуры диоксида углерода, показывающая тройную точку и критическую точку диоксида углерода.

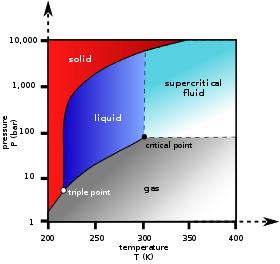
На фазовой диаграмме справа граничная кривая между областями жидкости и газа отображает ограничение между температурой и давлением, когда однокомпонентная система разделилась на жидкую и газовую фазы в равновесии. Единственный способ увеличить давление в двухфазной линии – это повышение температуры. Если температура снижается за счет охлаждения, часть газа конденсируется, снижая давление. На протяжении обоих процессов температура и давление остаются в зависимости, показанной этой граничной кривой, если только одна фаза не будет полностью поглощена испарением или конденсацией или пока не будет достигнута критическая точка . Пока существуют две фазы, существует только одна степень свободы, которая соответствует положению на фазовой граничной кривой.

Критической точкой является черная точка на конце границы жидкость–газ. По мере приближения к этой точке жидкая и газовая фазы становятся все более похожими, пока в критической точке больше не будет разделения на две фазы. Выше критической точки и вдали от кривой фазовой границы F = 2 , а температуру и давление можно контролировать независимо. Следовательно, существует только одна фаза, и она имеет физические свойства плотного газа, но ее также называют сверхкритической жидкостью .

Из других двухграничных кривых одна представляет собой границу твердого тела и жидкости или кривую температуры плавления , которая указывает на условия равновесия между этими двумя фазами, а другая, при более низких температуре и давлении, представляет собой границу твердого тела и газа.

Даже для чистого вещества возможно, что три фазы, такие как твердая, жидкая и пар, могут существовать вместе в равновесии ( P = 3 ). Если есть только один компонент, степеней свободы нет ( F = 0 ), когда есть три фазы. Следовательно, в однокомпонентной системе эта трехфазная смесь может существовать только при единых температуре и давлении, что известно как тройная точка . Здесь есть два уравнения µ _sol ( T , p ) = µ _liq ( T , p ) = µ _vap ( T , p ) , которых достаточно для определения двух переменных T и p. На диаграмме CO ₂ тройная точка — это точка, в которой соединяются твердая, жидкая и газовая фазы, при 5,2 бар и 217 К. Также возможно, что другие группы фаз образуют тройную точку, например, в В водной системе существует тройная точка, где лед I , лед III и жидкость могут сосуществовать.

Если бы четыре фазы чистого вещества находились в равновесии ( P = 4 ), правило фаз дало бы F = −1 , что бессмысленно, поскольку не может быть −1 независимых переменных. Этим объясняется тот факт, что четыре фазы чистого вещества (такие как лед I, лед III, жидкая вода и водяной пар) не находятся в равновесии ни при какой температуре и давлении. В терминах химических потенциалов теперь существуют три уравнения, которым вообще не могут быть удовлетворены никакие значения двух переменных Т и р , хотя в принципе они могут быть решены в частном случае, когда одно уравнение математически зависит от двух других. Однако на практике сосуществование большего количества фаз, чем разрешено правилом фаз, обычно означает, что не все фазы находятся в истинном равновесии.

Двухкомпонентные системы

Для бинарных смесей двух химически независимых компонентов C = 2 так что F = 4 - P. , Помимо температуры и давления, другой степенью свободы является состав каждой фазы, часто выражаемый мольной долей или массовой долей одного компонента.

Диаграмма точки кипения

В качестве примера рассмотрим систему двух полностью смешивающихся жидкостей, таких как толуол и бензол , находящихся в равновесии с их парами. Эту систему можно описать диаграммой температуры кипения , которая показывает состав (мольную долю) двух равновесных фаз в зависимости от температуры (при фиксированном давлении).

Четыре термодинамические переменные, которые могут описывать систему, включают температуру ( T ), давление ( p ), мольную долю компонента 1 (толуола) в жидкой фазе ( x _1L ) и мольную долю компонента 1 в паровой фазе ( x _1V ). . Однако, поскольку в равновесии присутствуют две фазы ( P = 2 ), только две из этих переменных могут быть независимыми ( F = 2 ). Это связано с тем, что четыре переменные ограничены двумя соотношениями: равенством химических потенциалов жидкого толуола и паров толуола и соответствующим равенством для бензола.

Для заданных T и p в равновесии будут две фазы, когда общий состав системы ( точка системы ) находится между двумя кривыми. Горизонтальная линия ( изотерма или соединительная линия) может быть проведена через любую такую ​​точку системы и пересекает кривую для каждой фазы при ее равновесном составе. Количество каждой фазы определяется правилом рычага (выраженным в переменной, соответствующей оси x , здесь мольная доля).

При анализе фракционной перегонки вместо этого рассматриваются две независимые переменные: состав жидкой фазы (x _1L ) и давление. равновесная температура ( температура кипения В этом случае правило фаз подразумевает, что определяются ) и состав паровой фазы.

жидкость–пар Фазовые диаграммы для других систем могут иметь азеотропы (максимумы или минимумы) на кривых состава, но применение правила фаз остается неизменным. Разница лишь в том, что составы двух фаз равны именно при азеотропном составе.

Водный раствор 4 видов солей

Рассмотрим водный раствор, содержащий хлорид натрия (NaCl), хлорид калия (KCl), бромид натрия (NaBr) и бромид калия (KBr), находящиеся в равновесии с соответствующими твердыми фазами. Каждая соль в твердой форме представляет собой отдельную фазу, поскольку каждая из них имеет различную кристаллическую структуру и состав. Водный раствор сам по себе является другой фазой, поскольку он образует гомогенную жидкую фазу, отдельную от твердых солей, со своим особым составом и физическими свойствами. Таким образом, мы имеем P = 5 фаз.

Присутствуют 6 элементов (H, O, Na, K, Cl, Br), но у нас есть 2 ограничения:

• Стехиометрия воды: n(H) = 2n(O).
• Баланс зарядов в растворе: n(Na) + n(K) = n(Cl) + n(Br).

давая C = 6 - 2 = 4 компонента. Правило фаз Гиббса гласит, что F = 1. Так, например, если мы построим фазовую диаграмму системы PT, существует только одна линия, на которой сосуществуют все фазы. Любое отклонение от линии приведет либо к полному растворению одной из солей, либо к полному осаждению одного из ионов из раствора.

фаз при

Для приложений в материаловедении, связанных с фазовыми изменениями между различными твердыми структурами, давление часто считается постоянным (например, при одной атмосфере) и игнорируется как степень свободы, поэтому формула принимает вид:

$F=C-P+1$

Иногда это неправильно называют «правилом конденсированной фазы», ​​но оно неприменимо к конденсированным системам , подверженным высоким давлениям (например, в геологии), поскольку влияние этих давлений важно.

Правило фаз в коллоидных смесях

В коллоидных смесях пятикратное и шесть очков были описаны с нарушением правила фаз Гиббса, но утверждается, что в этих системах это правило можно обобщить до $F=M+C-P+1$ где $M$ учитывает дополнительные параметры взаимодействия между компонентами, такие как диаметр одного типа частиц по отношению к диаметру других частиц в растворе.

Дальнейшее чтение

• Предель, Бруно; Хох, Майкл младший; Пул, Монте (14 сентября 2004 г.). Фазовые диаграммы и гетерогенные равновесия: Практическое введение . Спрингер. ISBN  3-540-14011-5 .
• Уайт, Мэри Энн (1999). Свойства материалов . Издательство Оксфордского университета (1999). ISBN  0-19-511331-4 . Глава 9. Термодинамические аспекты устойчивости.