Полуправильный многогранник

Фигуры Госсета

3D соты
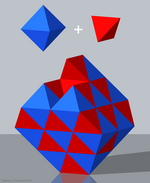Простая тетраоктаэдрическая проверка	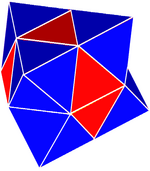Сложная тетраоктаэдрическая проверка
4D-многогранники
тетраоктаэдрический	Октикосаэдрический	Тетрикосаэдрический

В геометрии , по Торольда Госсета определению , полуправильный многогранник обычно считается многогранником , который является вершинно-транзитивным и все его грани которого являются правильными многогранниками . Э. Л. Эльте составил более длинный список в 1912 году под названием «Полуправильные многогранники гиперпространств», который включал более широкое определение.

Список Госсета

В трехмерном пространстве и ниже термины полуправильный многогранник и однородный многогранник имеют одинаковое значение, поскольку все однородные многоугольники должны быть правильными . Однако, поскольку не все однородные многогранники являются правильными , количество полуправильных многогранников в размерностях больше трех намного меньше, чем количество однородных многогранников в том же количестве измерений.

Три выпуклых полуправильных 4-многогранника — это выпрямленный 5-клеточный , курносый 24-клеточный и выпрямленный 600-ячеечный . Единственными полуправильными многогранниками в более высоких размерностях являются k ₂₁ многогранники , где выпрямленная 5-ячеечная клетка является частным случаем k = 0. Все они были перечислены Госсетом, но доказательство полноты этого списка не было опубликовано до тех пор, пока не была опубликована работа Макарова (1988) для четырех измерений и Blind & Blind (1991) для более высоких измерений.

4-многогранники Госсета (в скобках его имена)

Ректифицированный 5-клеточный (Тетроктаэдрический),

Ректифицированный 600-ячеечный (Октикосаэдрический),

Курносый 24-клеточный (Тетрикосаэдрический), , или

Полуправильные E-многогранники в более высоких размерностях

5-демикуб (5-ик полуправильный), 5-многогранник , ↔

2 ₂₁ многогранник (6-ic полуправильный), 6-многогранник , или

3 ₂₁ многогранник (7-ic полуправильный), 7-многогранник ,

4 ₂₁ многогранник (8-ic полуправильный), 8-многогранник ,

Евклидовы соты

Тетраэдрически -октаэдрические соты в евклидовом трехмерном пространстве имеют чередующиеся тетраэдрические и октаэдрические ячейки.

Полуправильные многогранники можно расширить до полуправильных сот . Полуправильные евклидовы соты представляют собой тетраэдрически-октаэдрические соты (3D), вращающиеся чередующиеся кубические соты (3D) и 5 ₂₁ соты (8D).

Госсета Соты :

1. Тетраэдрически-октаэдрические соты или чередующиеся кубические соты (Простая тетраоктаэдрическая проверка), ↔ (Также квазиправильный многогранник )
2. Закручивающиеся перемежающиеся кубические соты (сложная тетраоктаэдрическая клетка),

Полурегулярные электронные соты:

• 5 ₂₁ соты (проверка 9) (евклидовы соты 8D),

Госсет (1900) дополнительно допустил евклидовы соты как аспекты евклидовых сот более высокой размерности, дав следующие дополнительные цифры:

1. Гиперкубическая сотовая призма, названная Госсетом ( n – 1)-ной полупроверкой (аналог одного ряда или ряда шахматной доски).
2. Чередованные соты из шестиугольных плит (тетрооктаэдрическая полуклетка),

Гиперболические соты

Гиперболические тетраэдрически-октаэдрические соты имеют тетраэдрические и два типа октаэдрических ячеек.

Существуют также гиперболические однородные соты, состоящие только из правильных ячеек ( Coxeter & Whitrow 1950 ), в том числе:

• Гиперболические однородные соты , 3D соты:
  1. Чередованный порядок-5 кубических сот , ↔ (Также квазиправильный многогранник )
  2. Тетраэдрически-октаэдрические соты ,
  3. Соты тетраэдра-икосаэдра ,
• Паракомпактные однородные соты , 3D соты, которые включают в себя однородные мозаики в виде ячеек:
  1. Соты четырехгранные ректифицированные порядка 6 ,
  2. Ректифицированные квадратные соты для плитки ,
  3. Ректифицированные соты квадратной плитки порядка 4 , ↔
  4. Чередованный порядок-6 кубических сот , ↔ (также квазирегулярный)
  5. Перемежающиеся шестиугольные соты для плитки , ↔
  6. Шестиугольные соты чередующегося порядка 4 , ↔
  7. Шестиугольные соты чередующегося порядка 5 , ↔
  8. Шестиугольные соты чередующегося порядка 6 , ↔
  9. Чередованные квадратные соты для плитки , ↔ (также квазирегулярный)
  10. Кубическая плитка в виде сот ,
  11. Заказ-4 квадратных сотовых плитки , =
  12. Четырёхгранно-треугольная черепица-соты ,
• 9D гиперболические паракомпактные соты:
  1. 6 ₂₁ сот (проверка 10),

См. также

• Полуправильный многогранник

Ссылки

• Слепой, Г.; Слепой, Р. (1991). «Полуправильные многогранники». математические комментарии Гельветийские 66 (1): 150–154. дои : 10.1007/BF02566640 . МР   1090169 . S2CID   119695696 .
• Коксетер, HSM (1973). Правильные многогранники (3-е изд.). Нью-Йорк: Dover Publications. ISBN  0-486-61480-8 .
• Коксетер, HSM ; Уитроу, Дж.Дж. (1950). «Мировая структура и неевклидовы соты». Труды Королевского общества . 201 (1066): 417–437. Бибкод : 1950RSPSA.201..417C . дои : 10.1098/rspa.1950.0070 . МР   0041576 . S2CID   120322123 .
• Эльте, ЭЛ (1912). Полуправильные многогранники гиперпространств . Гронинген: Гронингенский университет. ISBN  1-4181-7968-Х .
• Госсет, Торольд (1900). «О правильных и полуправильных фигурах в пространстве n измерений». Вестник математики . 29 : 43–48.
• Макаров, П.В. (1988). «О выводе четырехмерных полуправильных многогранников». Вопросы Дискрет. Геом. Мат. Исслед. Акад. Наук. Форма . 103 : 139–150, 177. МР   0958024 .