Квантовая турбулентность

Квантовая турбулентность — это название турбулентного потока — хаотического движения жидкости при высоких скоростях потока — квантовых жидкостей , таких как сверхтекучие жидкости . Идея о том, что в сверхтекучей жидкости возможна некая форма турбулентности посредством квантованных вихревых линий, была впервые предложена Ричардом Фейнманом . Динамика квантовых жидкостей регулируется квантовой механикой , а не классической физикой, которая управляет классическими (обычными) жидкостями . Некоторые примеры квантовых жидкостей включают сверхтекучий гелий ( ⁴ Он и Купер пары ³ Он ), конденсаты Бозе-Эйнштейна (БЭК), поляритонные конденсаты и ядерные макароны , которые теоретически существуют внутри нейтронных звезд . Квантовые жидкости существуют при температурах ниже критической температуры. $T_{c}$ при котором конденсация Бозе-Эйнштейна имеет место.

Общие свойства сверхтекучих жидкостей

Рис. 1. Принципиальная схема жидкости (синего цвета) в цилиндрическом контейнере. Слева: кривая $C$ прослеживает замкнутый путь в односвязной области. Путь можно сократить до точки $P$, и поэтому можно применить теорему Стокса. Для квантовой жидкости это означает, что циркуляция исчезает. Справа: кривая $C$ прослеживает замкнутый путь в многосвязной области (т.е. с дырками). Путь не может быть сокращен из-за дыры, и поэтому теорема Стокса не выполняется, что приводит к ненулевой квантованной циркуляции. Для квантовой жидкости это предполагает, что вихревые структуры действуют как «дыры».

Рис. 2. Слева: Простая схема прямой вихревой линии в трехмерном пространстве с положительной циркуляцией. В центре: азимутальная скорость относительно радиуса. (i) показывает скорость жидкости при вращении твердого тела. (ii) показывает скорость вихря как в классической, так и в квантовой жидкости. (iii) сочетание (i) и (ii) для формирования модели вихря Ренкина для торнадо с ядром размером $a_{0}$. Справа: числовая плотность в зависимости от радиуса квантовой жидкости с вихрем. $a_{0}$. Уменьшение плотности можно наблюдать на небольшом радиусе. $r<a_{0}$. Количество $n_{s}$ представляет плотность жидкости достаточно далеко от ядра вихря $r>a_{0}$.

Рис. 3. Слева: Схема вихревого кольца радиуса. $R$ двигаясь со скоростью $v_{R}$. В центре: трехмерная схема квантового вихревого кольца. Скорость кольца создается самим кольцом, которое движется со скоростью, обратно пропорциональной радиусу кольца. Толщина кольца сильно преувеличена, чтобы можно было рассмотреть форму тора. В действительности для гелия II толщина составляет примерно $10^{-10}{\text{m}}$ . Справа: профиль скорости вихревого кольца в зависимости от его размера. Можно наблюдать обратную зависимость. Это говорит о том, что кольца меньшего размера движутся с гораздо большей скоростью, а кольца большего размера - с гораздо меньшей скоростью.

Турбулентность квантовых жидкостей изучалась в основном в двух квантовых жидкостях: жидком гелии и атомных конденсатах. Экспериментальные наблюдения были сделаны для двух стабильных изотопов гелия, обычного ⁴ Он и редкий ³ Он. Последний изотоп имеет две фазы, называемые A-фазой и B-фазой. А-фаза сильно анизотропна , и хотя она обладает очень интересными гидродинамическими свойствами, эксперименты по турбулентности проводились почти исключительно в В-фазе. Гелий сжижается при температуре примерно 4К. При этой температуре жидкость ведет себя как классическая жидкость с необычайно малой вязкостью, называемая гелием I. После дальнейшего охлаждения гелий I подвергается конденсации Бозе-Эйнштейна с образованием сверхтекучей жидкости, называемой гелием II. Критическая температура $T_{c}$ для бозе-эйнштейновской конденсации гелия равна 2,17К (при давлении насыщенного пара ), тогда как для ³ Он-Б.

Хотя в атомных конденсатах не так много экспериментальных подтверждений турбулентности, как в гелии, эксперименты проводились с рубидием , натрием , цезием , литием и другими элементами. Критическая температура для этих систем порядка микрокельвина.

Есть два фундаментальных свойства квантовых жидкостей, которые отличают их от классических жидкостей: сверхтекучесть и квантованная циркуляция.

Сверхтекучесть

Сверхтекучесть возникает как следствие закона дисперсии элементарных возбуждений, и жидкости, демонстрирующие такое поведение, текут без вязкости . Это жизненно важное свойство квантовой турбулентности, поскольку вязкость классических жидкостей вызывает рассеивание кинетической энергии в тепло, гася движение жидкости. Ландау предсказал, что если сверхтекучая жидкость течет быстрее определенной критической скорости, $v_{c}$ (или, альтернативно, объект движется быстрее, чем $v_{c}$ в статической жидкости) тепловые возбуждения (ротоны) испускаются, когда становится энергетически выгодно генерировать квазичастицы, в результате чего жидкость больше не проявляет сверхтекучих свойств. Для гелия II эта критическая скорость равна $v_{c}\approx 60{\text{m/s}}$.

Квантованный тираж

Свойство квантованной циркуляции возникает как следствие существования и единственности сложной макроскопической волновой функции. $\Psi$, что завихренность очень сильно влияет на (локальное вращение), что делает его решающим для квантовой турбулентности.

Скорость и плотность жидкости можно восстановить по волновой функции $\Psi (\mathbf {x} ,t)$ написав это в полярной форме $\Psi (\mathbf {x} ,t)=|\Psi (\mathbf {x} ,t)|e^{i\phi (\mathbf {x} ,t)}$, где $|\Psi |$ это величина $\Psi$ и $\phi$ это фаза. Тогда скорость жидкости равна $\mathbf {v} (\mathbf {x} ,t)=(\hbar /m)\nabla \phi$, а плотность числа равна $n(\mathbf {x} ,t)=|\Psi |^{2}$. Плотность массы связана с плотностью числа соотношением $\rho (\mathbf {x} ,t)=mn$, где $m$ — масса одного бозона .

Тираж ​ $\Gamma$ определяется как линейный интеграл по простому замкнутому пути $C$ внутри жидкости

$\Gamma =\oint _{C}\mathbf {v} \cdot \mathbf {dr}$

Для односвязной поверхности $S$, теорема Стокса справедлива, и циркуляция исчезает, поскольку скорость можно выразить как градиент фазы. Для многосвязной поверхности разность фаз между произвольной начальной точкой кривой $C$ и конечная точка (то же, что и начальная точка, как $C$ закрыто) должно быть $2\pi q$, где $q=0,1,2,\cdots$ для того, чтобы волновая функция была однозначной. Это приводит к квантованному значению циркуляции

$\Gamma ={\frac {\hbar }{m}}\oint _{C}\nabla S\cdot \mathbf {dr} =q\kappa$

где $\kappa =h/m$ – квант обращения , а целое число $q$ - заряд (или число витков) вихря. Многозарядные вихри ( $q>1$) в гелии II нестабильны и по этой причине в большинстве практических приложений $q=1$. Для жидкости энергетически выгодно образование $q$ однозарядные вихри, а не одиночный вихрь заряда $q$, и поэтому многозарядный вихрь разделится на однозарядные вихри. При определенных условиях можно генерировать определенные вихри с зарядом выше 1.

Свойства вихревых линий

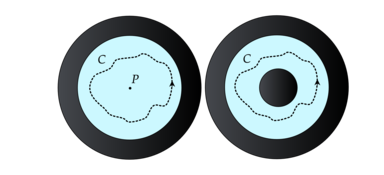
Вихревые линии представляют собой дефекты топологических линий фазы. Их зарождение превращает область квантовой жидкости в многосвязную область. Как показано на рис. 2, вблизи оси можно наблюдать обеднение плотности, при этом $\rho =0$ на вихревой линии. Размер ядра вихря варьируется в зависимости от квантовой жидкости. Размер ядра вихря составляет около $a_{0}=10^{-10}{\text{m}}$ для гелия II, $a_{0}=10^{-8}{\text{m}}$ для ³ He-B и для типичных атомных конденсатов $a_{0}=10^{-4}{\text{m}}$. Простейшая вихревая система в квантовой жидкости состоит из одной прямой вихревой линии; поле скорости такой конфигурации чисто азимутальное, определяемое выражением $v_{\theta }=\kappa /{2\pi r}$. Это та же формула, что и для классического решения вихревой линии уравнения Эйлера, однако классически эта модель физически нереалистична, поскольку скорость расходится как $r\rightarrow 0$. Это приводит к идее вихря Ренкина , показанного на рис. 2, который сочетает в себе вращение твердого тела для малых $r$ и вихревое движение при больших значениях $r$, и является более реалистичной моделью обычных классических вихрей.

Можно провести много общего с вихрями в классических жидкостях, например тот факт, что вихревые линии подчиняются классической теореме о циркуляции Кельвина : циркуляция сохраняется, и вихревые линии должны заканчиваться на границах или существовать в форме замкнутых петель. В пределе нулевой температуры точка вихревой линии будет двигаться соответственно полю скорости, которое создается в этой точке другими частями вихревой линии, при условии, что вихревая линия не является прямой (изолированный прямой вихрь не движется). ). Скорость также может создаваться любыми другими вихревыми линиями в жидкости - явление, также присутствующее в классических жидкостях. Простым примером этого является вихревое кольцо (вихрь в форме тора), которое движется с самоиндуцированной скоростью. $v_{R}$ обратно пропорциональна радиусу кольца $R$, где $R>>a_{0}$. Все кольцо движется со скоростью

$v_{R}={\frac {\kappa }{4\pi R}}\left[\ln {\left({\frac {8R}{a_{0}}}\right)}-{\frac {1}{2}}\right]$

Волны Кельвина

Рис. 4. Слева: Схема волны Кельвина с амплитудой. $A$ и длина волны $\lambda$. Справа: прямая вихревая конфигурация, преобразованная в изогнутую вихревую конфигурацию.

Рис. 5. Схема вихревого пересоединения двух вихрей. Стрелки на вихрях показывают направление завихренности в вихревой линии. Слева: До переподключения. В центре: происходит пересоединение вихрей. Справа: после переподключения.

Вихри в квантовых жидкостях поддерживают волны Кельвина, которые представляют собой спиральные возмущения вихревой линии, отличающиеся от ее прямой конфигурации и вращающиеся с угловой скоростью. $\omega$, с

$\omega \approx {\frac {\kappa k^{2}}{4\pi }}\ln {\left({\frac {1}{ka_{0}}}\right)}$

Здесь $k=2\pi /\lambda$ где $\lambda$ длина волны и $k$ волновой вектор.

Путешествующие вихри в квантовых жидкостях могут взаимодействовать друг с другом, что приводит к пересоединению вихревых линий и, в конечном итоге, к изменению топологии вихревой конфигурации при их столкновении, как предположил Ричард Фейнман. При отличных от нуля температурах вихревые линии рассеивают тепловые возбуждения, что создает силу трения с нормальной жидкой составляющей (тепловым облаком для атомных конденсатов). Это явление приводит к диссипации кинетической энергии. Например, вихревые кольца сожмутся, а волны Кельвина уменьшатся в амплитуде.

Вихревая решетка

Рис. 6. Схема цилиндрического контейнера, вращающегося со скоростью $\Omega$, образующая вихревую решетку из шести прямых вихревых линий.

Вихревые решетки представляют собой ламинарные (упорядоченные) конфигурации вихревых линий, которые можно создать путем вращения системы. Для цилиндрического сосуда радиуса $R$, то условие образования вихревой решетки можно получить, минимизировав выражение $F'=F-\mathbf {L} _{v}\cdot \mathbf {\Omega }$, где $F$ это свободная энергия, $\mathbf {L} _{v}$ - угловой момент жидкости и $\mathbf {\Omega }$ это вращение с величиной $\Omega$ и осевом направлении. Тогда критическая скорость возникновения вихревой решетки равна $\Omega _{c}^{1}={\frac {\kappa }{R^{2}}}\ln {\left({\frac {R}{a_{0}}}\right)}$.

Превышение этой скорости приводит к образованию вихря в жидкости. Состояния с большим количеством вихрей могут быть сформированы за счет дальнейшего увеличения вращения после следующих критических скоростей. $\Omega _{c}^{2},\,\Omega _{c}^{3},\cdots$. Вихри образуют упорядоченные конфигурации, называемые вихревыми решетками.

Две текучие природы

Рис. 7. График зависимости долей компонентов от температуры, показывающий смесь нормальной жидкости и сверхтекучей жидкости в гелии II, где $\rho _{s}/\rho$ – сверхтекучая фракция, а $\rho _{n}/\rho$ это нормальная фракция жидкости. При температурах выше критической температура вся жидкость составляет нормальную жидкость.

При ненулевой температуре $T$необходимо учитывать тепловые эффекты. Для атомарных газов при ненулевых температурах часть атомов не входит в состав конденсата, а образует разреженное (с большой длиной свободного пробега) тепловое облако, сосуществующее с конденсатом (которое в первом приближении может отождествляться со сверхтекучей составляющей). Поскольку гелий — это жидкость, а не разбавленный газ, как атомные конденсаты, между атомами существует гораздо более сильное взаимодействие, и конденсат — это лишь часть сверхтекучей компоненты. Тепловые возбуждения (состоящие из фононов и ротонов) образуют компонент вязкой жидкости (очень короткий средний путь свободного пробега, аналог классической вязкой жидкости, определяемой уравнением Навье-Стокса ), называемый нормальной жидкостью, который сосуществует со сверхтекучим компонентом. Это составляет основу теории двух жидкостей Тисы и Ландау , описывающей гелий II как смесь совместно проникающих компонентов сверхтекучей и нормальной жидкости с общей плотностью, определяемой уравнением $\rho =\rho _{n}+\rho _{s}$. В таблице представлены основные свойства компонентов сверхтекучей и нормальной жидкости:

Компонент	скорость	плотность	энтропия	вязкость
сверхтекучий	$\mathbf {v} _{s}$	$\rho _{s}$	ноль	ноль
классическая жидкость	$\mathbf {v} _{n}$	$\rho _{n}$	$S$	$\mu$

Относительные пропорции двух компонентов изменяются с температурой, от нормального потока жидкости при температуре перехода. $T_{c}$ ( $\rho _{n}/\rho \rightarrow 1$ и $\rho _{s}/\rho \rightarrow 0$), до полного сверхтекучего течения в пределе нулевой температуры ( $\rho _{s}/\rho \rightarrow 1$ и $\rho _{n}/\rho \rightarrow 0$). При малых скоростях уравнения двух жидкостей имеют вид

${\frac {\partial \rho }{\partial t}}+\nabla \cdot (\rho _{s}\mathbf {v} _{s}+\rho _{n}\mathbf {v} _{n})=0$

${\frac {\partial (\rho S)}{\partial t}}+\nabla \cdot (\rho S\mathbf {v} _{n})=0$

$\rho _{s}\left[{\frac {\partial \mathbf {v} _{s}}{\partial t}}+(\mathbf {v} _{s}\cdot \nabla )\mathbf {v} _{s}\right]=-{\frac {\rho _{s}}{\rho }}\nabla P+\rho _{s}S\nabla T$

$\rho _{n}\left[{\frac {\partial \mathbf {v} _{n}}{\partial t}}+(\mathbf {v} _{n}\cdot \nabla )\mathbf {v} _{n}\right]=-{\frac {\rho _{n}}{\rho }}\nabla P-\rho _{s}S\nabla T+\mu \nabla ^{2}\mathbf {v} _{n}$

где здесь $P$ это давление, $S$ - энтропия на единицу массы и $\mu$ — вязкость обычного жидкого компонента, как указано в таблице выше. Первое из этих уравнений можно определить как уравнение сохранения массы , а второе уравнение — как сохранение энтропии. Результаты этих уравнений приводят к явлениям второго звука и теплового противотока. При больших скоростях сверхтекучая жидкость становится турбулентной и появляются вихревые линии; при еще больших скоростях как нормальная жидкость, так и сверхтекучая жидкость становятся турбулентными.

Классическая

Рис. 8. Принципиальная схема колмогоровского энергетического каскада внутри аэродинамической трубы. Нагнетание воздуха происходит при $k_{D}=2\pi /D$ где $D$ размер аэродинамической трубы. Количество $k_{\eta }$, волновое число Колмогорова, — это значение в k-пространстве, связанное с колмогоровским масштабом длины , точкой, в которой турбулентная кинетическая энергия рассеивается в тепло.

Эксперименты и численные решения показывают, что квантовая турбулентность представляет собой, по-видимому, случайный клубок вихревых линий внутри квантовой жидкости. Изучение квантовой турбулентности направлено на изучение двух основных вопросов:

1. Действительно ли вихревые клубки случайны или содержат в себе какие-то характерные свойства или организованные структуры?
2. Чем квантовая турбулентность отличается от классической турбулентности?

Чтобы понять квантовую турбулентность, полезно установить связь с турбулентностью классических жидкостей. Турбулентность классических жидкостей — обычное явление, которое легко наблюдать в течении ручья или реки, как это впервые сделал Леонардо да Винчи в своих знаменитых зарисовках. При включении водопроводного крана можно заметить, что сначала вода вытекает равномерно (так называемый ламинарный поток), но если кран повернуть на большую скорость, то поток украшается неравномерными выпуклостями, непредсказуемо распадающимися на множество пряди, когда они разбрызгиваются постоянно меняющимся потоком, известным как турбулентный поток. Леонардо да Винчи впервые заметил и отметил в своих личных записных книжках, что турбулентные потоки классических жидкостей включают области циркулирующей жидкости, называемые вихрями (или водоворотами).

Простейшим случаем классической турбулентности является гомогенная изотропная турбулентность (HIT), находящаяся в статистическом устойчивом состоянии. Такая турбулентность может быть создана внутри аэродинамической трубы , например канала, в котором поток воздуха перемещается вентилятором с одной стороны на другую. Его часто оснащают сеткой для создания турбулентного потока воздуха. Статистически устойчивое состояние обеспечивает стабилизацию основных свойств потока, даже если они локально колеблются. Из-за наличия вязкости без непрерывного подвода энергии турбулентность потока будет затухать из-за сил трения. В аэродинамической трубе энергия постоянно подается вентилятором. Полезно ввести понятие распределения энергии по масштабам длины волнового вектора $\mathbf {k} =(k_{x},k_{y},k_{z})$и волновое число $k=|\mathbf {k} |$. В одном измерении волновое число можно связать с длиной волны, просто используя $k=2\pi /\lambda$. Полная энергия $E_{tot}$ на единицу массы определяется выражением

$E_{tot}={\frac {1}{\mathcal {V}}}\int _{\mathcal {V}}{\frac {\mathbf {v} ^{2}}{2}}\,\mathrm {d} ^{3}\mathbf {r} =\int _{0}^{\infty }E(k)\,\mathrm {d} k$

где $E(k)$ — энергетический спектр , по существу представляющий распределение турбулентной кинетической энергии по волновым числам. Идея каскада энергии , при которой происходит передача энергии от крупномасштабных вихрей к вихрям меньшего масштаба, что в конечном итоге приводит к вязкой диссипации, была замечательно отмечена Льюисом Фраем Ричардсоном . Диссипация происходит на масштабах длины диссипации $\eta$ (называемый масштабом длины Колмогорова), где $\eta =(\nu ^{3}/\varepsilon )^{1/4}$ где $\nu$ – кинематическая вязкость. Пионерской работой Андрея Колмогорова был найден энергетический спектр, имеющий вид

$E(k)=C\varepsilon ^{\frac {2}{3}}k^{-{\frac {5}{3}}}$

где $\varepsilon$ - скорость диссипации энергии на единицу объема $-\mathrm {d} E/\mathrm {d} t$. Константа $C$ – безразмерная константа, принимающая значение $C\approx 1.5$. В k-пространстве значение, связанное с масштабом длины Колмогорова, представляет собой волновое число Колмогорова. $k_{\eta }$, где происходит вязкая диссипация.

в квантовых

Рис 9а. Численно смоделированный вихревой клубок, представляющий колмогоровскую квантовую турбулентность. Тонкие линии представляют собой вихревые линии внутри кубического контейнера. Цветовая полоса представляет собой величину нелокального взаимодействия, т.е. степень влияния на участок вихревой линии других окружающих его вихревых линий. (Кредит AW Baggaley)

Рис. 9. Принципиальная схема энергетического спектра колмогоровской турбулентности при очень малых температурах. $k^{-5/3}$ энергетический каскад присутствует на больших масштабах длины, а волновой каскад Кельвина можно наблюдать на очень малых масштабах длины, который подвергается излучению звука. Накопление узких мест происходит в масштабе квантовой длины. $\ell$.

При температурах, достаточно низких для того, чтобы квантово-механические эффекты управляли жидкостью, квантовая турбулентность представляет собой, казалось бы, хаотичный клубок вихревых линий с сильно запутанной топологией, которые перемещают друг друга и воссоединяются при столкновении. В чистой сверхтекучей жидкости нет нормального компонента, несущего энтропию системы, и поэтому жидкость течет без вязкости, что приводит к отсутствию масштаба диссипации. $\eta$. Аналогично классическим жидкостям, квантовая шкала длин $\ell$ (и соответствующее значение в k-пространстве $k_{\ell }$) можно ввести, заменив в колмогоровской шкале длин кинематическую вязкость квантом циркуляции $\kappa$. Для масштабов более $\ell$, небольшая поляризация вихревых линий обеспечивает растяжение, необходимое для поддержания колмогоровского энергетического каскада.

В сверхтекучем гелии II были проведены эксперименты по созданию турбулентности, ведущей себя в соответствии с каскадом Колмогорова. Одним из таких примеров является случай двух пропеллеров, вращающихся в противоположных направлениях. где как выше, так и ниже критической температуры $T_{c}$ наблюдался колмогоровский энергетический спектр, неотличимый от спектров, наблюдаемых при турбулентности классических жидкостей. При более высоких температурах существование нормального жидкого компонента приводит к появлению сил вязкости и возможному рассеянию тепла, которое нагревает систему. В результате этого трения вихри становятся более гладкими, а волны Кельвина, возникающие в результате пересоединения вихрей, более гладкими, чем в низкотемпературной квантовой турбулентности. Колмогоровская турбулентность возникает в квантовых жидкостях при подводе энергии на больших масштабах длины, где энергетический спектр соответствует $k^{-5/3}$ в инерционном диапазоне $k_{D}<k<k_{\ell }$. Для масштабов длины менее $\ell$, вместо этого энергетический спектр следует $k^{-1}$ режим.

При температурах в нулевом пределе незатухающие волны Кельвина приводят к появлению большего количества изломов в форме вихрей. Для больших масштабов длины квантовая турбулентность проявляется как каскад колмогоровской энергии (численное моделирование с использованием уравнения Гросса-Питаевского и модель вихревой нити подтвердила этот эффект ), с энергетическим спектром, следующим $k^{-5/3}$. В отсутствие тепловыделения интуитивно понятно предположить, что квантовая турбулентность в пределе низких температур не затухает, как при более высоких температурах, однако экспериментальные данные показали, что это не так: квантовая турбулентность затухает даже при очень низких температурах. Волны Кельвина взаимодействуют и создают более короткие волны Кельвина, пока они не станут достаточно короткими, чтобы испускать звук (фононы), что приводит к преобразованию кинетической энергии в тепло и, таким образом, к рассеянию энергии. Этот процесс, который смещает энергию во все меньшие и меньшие масштабы длины при волновых числах, больших $k_{\ell }$ называется волновым каскадом Кельвина и протекает на отдельных вихрях. Таким образом, низкотемпературная квантовая турбулентность должна состоять из двойного каскада: колмогоровского режима (каскада вихрей) в инерционном диапазоне $k_{D}<k<k_{\ell }$, за которым следует узкое плато, за которым следует волновой каскад Кельвина (каскад волн), подчиняющийся тому же $k^{-5/3}$ закон, но с другим физическим происхождением. В настоящее время это общепринятое мнение, но следует подчеркнуть, что оно вытекает только из теории и численного моделирования: в настоящее время нет прямых экспериментальных доказательств волнового каскада Кельвина из-за сложности наблюдения и измерения на таких малых масштабах длины.

Винная турбулентность

Рис 9б. Численно смоделированный вихревой клубок, представляющий квантовую турбулентность Винена. Тонкие линии представляют собой вихревые линии внутри кубического контейнера. Цветовая полоса представляет собой величину нелокального взаимодействия, т.е. степень влияния на участок вихревой линии других окружающих его вихревых линий. (Кредит AW Baggaley)

Рис. 10. Принципиальная схема энергетического спектра винной турбулентности. А $k^{-1}$ Режим можно наблюдать для очень больших волновых чисел, при этом пик энергетического спектра приходится на волновое число $k_{\ell }$ связанный с масштабом квантовой длины $\ell$. Зеленая линия представляет собой $k^{-5/3}$ режим для сравнения.

Турбулентность Винена может быть создана в квантовой жидкости путем введения вихревых колец в систему, что наблюдалось как численно, так и экспериментально. Это наблюдалось также при численном моделировании турбулентного гелия II, движимого небольшим тепловым потоком, и при численном моделировании захваченных атомных конденсатов Бозе-Эйнштейна; оно было обнаружено даже при численных исследованиях сверхтекучих моделей ранней Вселенной. В отличие от режима Колмогорова, который, по-видимому, имеет классический аналог, турбулентность Винена не была обнаружена в классической турбулентности.

Турбулентность Винена возникает при очень низких энерговложениях в систему, что предотвращает образование крупномасштабных частично поляризованных структур, которые преобладают в колмогоровской турбулентности, как показано на рис. 9а. Частичная поляризация вносит большой вклад в количество нелокальных взаимодействий между вихревыми линиями, которые можно видеть на рисунке. Напротив, на рис. 9б показан режим турбулентности Винена, в котором нелокальное взаимодействие очень незначительное. Энергетический спектр пиков турбулентности Винена на промежуточных масштабах около $k_{\ell }$, а не на больших масштабах длины $k_{D}$. Из рис. 10 видно, что для малых масштабов турбулентность следует типичному типу. $k^{-1}$ поведение изолированного вихря. В результате этих свойств турбулентность Винена выглядит как почти полностью случайный поток с очень слабым или незначительным каскадом энергии.

Распад

Исходя из разных сигнатур, турбулентность Колмогорова и Винена подчиняется степенным законам, связанным с их временным затуханием. Для режима Колмогорова после устранения воздействия, поддерживающего турбулентность в статистическом установившемся состоянии, затухание $E(t)\sim t^{-2}$ для энергии и $L(t)\sim t^{-3/2}$ для плотности вихревых линий (определяемой как длина вихря в единице объема). Турбулентность Винена затухает во времени медленнее, чем турбулентность Колмогорова: энергия затухает по мере $E(t)\sim t^{-1}$ а плотность вихревых линий как $L(t)\sim t^{-1}$.

Турбулентность в атомных конденсатах

Компьютерное моделирование сыграло особенно важную роль в развитии теоретического понимания квантовой турбулентности.

Турбулентность в атомных конденсатах изучалась совсем недавно, а это означает, что доступной информации меньше. Турбулентные атомные конденсаты содержат гораздо меньшее количество вихрей по сравнению с турбулентностью в гелии. Из-за небольшого размера типичных атомных конденсатов не существует большого разделения по длине между размером системы и размером между вихрями, и поэтому k-пространство ограничено. Численное моделирование показывает, что турбулентность с большей вероятностью появится в режиме Винена. Эксперименты, проведенные в Кембридже, также обнаружили появление масштабирования волновой турбулентности.

Генерация и обнаружение квантовой турбулентности

генерация

Рис. 11. Смоделированный вихревой клубок, представляющий квантовую турбулентность в кубическом объеме и показывающий квантованные вихри.

Существует множество методов, которые можно использовать для создания вихревого клубка (показанного на рис. 11) в лаборатории. Здесь они перечислены по квантовой жидкости, в которой они могут быть созданы.

QT в гелии II

• Внезапное буксирование сетки в образце покоящейся жидкости.
• Перемещение жидкости по трубам или каналам с помощью сильфонов или насосов, создание сверхтекучей аэродинамической трубы (эксперимент TOUPIE в Гренобле )
• Вращение одного или двух пропеллеров внутри контейнера; конфигурация двух пропеллеров, вращающихся в противоположных направлениях, называется «поток Кармана» (например, эксперимент ШРЕК в Гренобле).
• Создание ударных волн и кавитации за счет локальной фокусировки ультразвука (это позволяет генерировать квантовую турбулентность вдали от границ)
• Колеблющиеся/вибрирующие вилки или провода
• Применение теплового потока (также называемого «тепловым противотоком »). ): прототип эксперимента представляет собой канал, который с одного конца открыт для гелиевой ванны, а противоположный конец закрыт и имеет резистор . Электрический ток проходит через резистор и генерирует омическое тепло ; тепло переносится от нагревателя к ванне обычным жидким компонентом, в то время как сверхтекучий движется к нагревателю, так что чистый массовый поток равен нулю, поскольку канал закрыт. Относительная скорость $v_{ns}=|v_{n}-v_{s}|$ (Противоток) двух компонентов жидкости устанавливается таким образом, который пропорционален приложенному теплу. Выше малого критического значения скорости противотока формируется турбулентный вихревой клубок.
• Инжектирование вихревых колец (кольца генерируются путем инжекции электронов, которые образуют небольшой пузырь размером около 16 Ангстрем , который ускоряется электрическим полем до тех пор, пока при превышении критической скорости не зародится вихревое кольцо)

QT в ³ He-B

В ³ He-B, квантовая турбулентность может создаваться вибрацией проводов. В атомных конденсатах квантовая турбулентность может создаваться встряхиванием или колебанием ловушки, удерживающей БЭК. и путем фазового импринтинга квантовых вихрей.

Обнаружение

В классической турбулентности обычно измеряют скорость либо в фиксированном положении в зависимости от времени (типично для физических экспериментов), либо одновременно во многих положениях (типично для численного моделирования). Квантовая турбулентность характеризуется неупорядоченным клубком дискретных (индивидуальных) вихревых линий.

В гелии II существует методика измерения плотности вихревых линий. $L$ (длина вихревых линий на единицу объема, основанная на обнаружении второго затухания звука. Среднее расстояние между вихревыми линиями, $\ell$, можно найти через плотность вихревых линий как $\ell =1/{\sqrt {L}}$ .

Обнаружение в гелии II

• Измерение затухания вторых звуковых волн
• Измерение градиентов температуры или давления
• Измерение ионов, захваченных вихрями
• Использование частиц-индикаторов (небольших стеклянных или пластиковых сфер/твердых водородных снежков) размером порядка микрона, а затем их визуализация с помощью лазеров. Можно использовать следующие методы: PIV (скорость изображения частиц) или PTV (скорость отслеживания частиц). Совсем недавно стали использовать эксимерные молекулы гелия.
• Использование колеблющихся вилок
• Использование консолей
• Использование криогенных горячих проводов

Обнаружение в ³ He-B

Квантовую турбулентность можно обнаружить в ³ He-B двумя способами: ядерный магнитный резонанс (ЯМР). и андреевское рассеяние тепловых квазичастиц. Для атомных конденсатов типично, что конденсат необходимо расширить (путем отключения потенциала захвата) так, чтобы он стал достаточно большим, чтобы можно было получить изображение. Недостаток этой процедуры заключается в том, что она приводит к разрушению конденсата. В результате получается двумерное изображение, которое позволяет изучать двумерную квантовую турбулентность, но накладывает ограничения на изучение трехмерной квантовой турбулентности с использованием этого метода. Отдельные квантовые вихри наблюдались в трех измерениях, перемещаясь и воссоединяясь с использованием метода, который извлекает небольшие доли конденсата за раз, что позволяет наблюдать временную последовательность одной и той же конфигурации вихрей.

См. также

• Сверхтекучий гелий-4
• Макроскопические квантовые явления
• Квантовый вихрь
• Квантовая гидродинамика
• 2D квантовая турбулентность