Динамика неидеальной сжимаемой жидкости

Динамика неидеальной сжимаемой жидкости ( NICFD ), или динамика неидеального газа , — это раздел механики жидкости , изучающий динамическое поведение жидкостей, не подчиняющихся термодинамике идеального газа . Это, например, случай плотных паров , сверхкритических потоков и сжимаемых двухфазных потоков . Термином «плотные пары» мы обозначаем все жидкости в газообразном состоянии, характеризующиеся термодинамическими условиями, близкими к насыщению и критической точке . ^[1] Вместо этого сверхкритические жидкости имеют значения давления и температуры, превышающие их критические значения. ^[2] тогда как двухфазные потоки характеризуются одновременным присутствием как жидкой, так и газовой фаз. ^[3]

Во всех этих случаях жидкость необходимо моделировать как реальный газ , поскольку ее термодинамическое поведение значительно отличается от поведения идеального газа, которое, напротив, проявляется в разбавленных термодинамических условиях. Закон идеального газа в целом можно использовать как разумное приближение термодинамики жидкости при низких давлениях и высоких температурах. В противном случае межмолекулярные силы и размеры частиц жидкости, которыми пренебрегают в приближении идеального газа, становятся актуальными и могут существенно повлиять на поведение жидкости. ^[4] Это чрезвычайно справедливо для газов, состоящих из сложных и тяжелых молекул, которые имеют тенденцию больше отклоняться от идеальной модели. ^[5]

Хотя гидродинамика сжимаемых потоков в идеальных условиях хорошо известна и характеризуется несколькими аналитическими результатами, ^[6] при рассмотрении неидеальных термодинамических условий возможно возникновение своеобразных явлений. Это особенно справедливо в сверхзвуковых условиях, а именно при скоростях потока, превышающих скорость звука в рассматриваемой жидкости. На все типичные особенности сверхзвуковых течений влияет неидеальная термодинамика, что приводит как к количественным, так и к качественным отличиям от динамики идеального газа. ^[7]

Неидеальная термодинамика

идеального газа Для разбавленных термодинамических условий уравнение состояния (EoS) обеспечивает достаточно точные результаты при моделировании термодинамики жидкости. Обычно это происходит при низких значениях приведенного давления и высоких значениях приведенной температуры, где термин «приведенная» относится к отношению определенной термодинамической величины и ее критического значения. Для некоторых жидкостей, таких как воздух, предположение об идеальных условиях вполне разумно и широко используется. ^[6]

С другой стороны, когда термодинамические условия приближаются к конденсации и критической точке или когда задействованы высокие давления, необходимы модели реального газа, чтобы отразить реальное поведение жидкости. Фактически в этих условиях в игру вступают межмолекулярные силы и эффекты сжимаемости. ^[4]

Мерой неидеальности жидкости является коэффициент сжимаемости. $Z$ , ^[8] определяется как

Z={\frac {Pv}{RT}}

где

$P$ – давление [Па];
$v$ - удельный объем [м ³/кг];
$R$ - удельная газовая постоянная [Дж/(кг К)], а именно универсальная газовая постоянная, деленная на молекулярную массу жидкости;
$T$ — абсолютная температура [К].

Коэффициент сжимаемости — безразмерная величина , равная 1 для идеальных газов и отклоняющаяся от единицы с увеличением степени неидеальности. ^[9]

Существует несколько неидеальных моделей, основанных на простейших кубических уравнениях состояния (таких как уравнение Ван-дер-Ваальса). ^[4]^[10] и Пэн-Робинсон ^[11] модели) до сложных многопараметрических, включая уравнение состояния Спана-Вагнера. ^[12]^[13]

Современные уравнения состояния легко доступны через термодинамические библиотеки, такие как FluidProp или программное обеспечение с открытым исходным кодом CoolProp. ^[14]

Неидеальные газодинамические режимы

Динамическое поведение сжимаемых течений определяется безразмерной термодинамической величиной $\Gamma$ , которая известна как производная Ландау или фундаментальная производная газовой динамики. ^[15]^[16] и определяется как

\Gamma ={\frac {v^{3}}{2c^{2}}}\left({\frac {\partial ^{2}P}{\partial v^{2}}}\right)_{s}=1+{\frac {c}{v}}\left({\frac {\partial c}{\partial P}}\right)_{s}

где

$c$ – скорость звука [м/с];
$s$ — удельная энтропия на единицу массы [Дж/(кг К)].

С математической точки зрения производная Ландау представляет собой безразмерную меру кривизны изэнтроп в термодинамической плоскости давление-объем . С физической точки зрения определение $\Gamma$ говорит о том, что скорость звука увеличивается с давлением при изэнтропических преобразованиях для значений $\Gamma >1$ , тогда как она, напротив, уменьшается с давлением для $\Gamma <1$ .

На основании стоимости $\Gamma$ можно определить три газодинамических режима: ^[16]

идеальный газодинамический режим для $\Gamma >1$ ;
неидеальный классический газодинамический режим для $0<\Gamma <1$ ;
неклассический газодинамический режим для $\Gamma <0$ .

Идеальный газодинамический режим

В идеальном режиме качественно восстанавливается обычное поведение идеального газа. Фактически для идеального газа значение производной Ландау сводится к постоянному значению $\Gamma ={\frac {\gamma +1}{2}}$ , где $\gamma$ - коэффициент теплоемкости . По определению, $\gamma$ - это отношение между постоянным давлением и удельной теплоемкостью постоянного объема , поэтому оно больше 1, что приводит к значению $\Gamma$ тоже больше 1. ^[6]

В этом режиме встречаются только количественные различия по отношению к идеальной модели. Эволюция потока фактически зависит от полных, или стагнационных , термодинамических условий. Например, эволюция числа Маха идеального газа в сверхзвуковом сопле зависит только от соотношения теплоемкостей (а именно жидкости) и от соотношения давлений выхлопа и торможения. ^[6] Вместо этого, учитывая эффекты реального газа, даже при фиксировании жидкости и соотношения давлений, разные полные состояния дают разные профили Маха. ^[17]

Обычно для однофазных жидкостей, состоящих из простых молекул, можно достичь только идеального газодинамического режима, даже для термодинамических условий, очень близких к насыщению. Это, например, случай двухатомных или трехатомных молекул, таких как азот или углекислый газ , поведение которых может лишь незначительно отклоняться от идеального. ^[5]

Неидеальный классический газодинамический режим

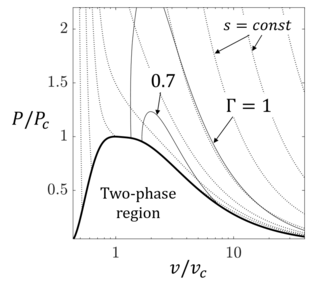
Для жидкостей с высокой молекулярной сложностью современные термодинамические модели предсказывают значения $0<\Gamma <1$ в однофазной области, близкой к кривой насыщения, где скорость звука в значительной степени чувствительна к изменению плотности вдоль изэнтроп. ^[18] Такие жидкости относятся к разным классам химических соединений , включая углеводороды , силоксаны и хладагенты . ^[5]^[18]

В неидеальном режиме могут быть обнаружены даже качественные различия по сравнению с идеальной газодинамикой, а это означает, что эволюция потока может сильно отличаться при различных общих условиях. Наиболее своеобразным явлением неидеального режима является уменьшение числа Маха при изэнтропических расширениях, происходящих в сверхзвуковом режиме, а именно процессы, при которых плотность жидкости уменьшается. ^[19] Действительно, для идеального газа, расширяющегося изэнтропически в сужающемся-расширяющемся сопле, число Маха монотонно возрастает с уменьшением плотности. ^[6] Напротив, для течений, развивающихся в неидеальном режиме, на расширяющемся участке возможна немонотонная эволюция числа Маха, тогда как уменьшение плотности остается монотонным (см. рисунок в заглавном разделе). Это частное явление определяется величиной $J$ , которая является безразмерной мерой производной числа Маха по плотности в изэнтропических процессах: ^[19]

J={\frac {\rho }{M}}{\frac {dM}{d\rho }}=1-\Gamma -{\frac {1}{M^{2}}}

где

$M$ – число Маха;
$\rho$ плотность [кг/м ³].

Из определения $J$ , число Маха увеличивается с увеличением плотности для условий течения со значениями $J>0$ . Действительно, это возможно только для значений $\Gamma <1$ , то есть в неидеальном режиме. Однако это не является достаточным условием появления немонотонного числа Маха, поскольку достаточно большое значение $M$ также требуется. В частности, сверхзвуковые условия ( $M>1$ ) необходимы. ^[19]

Аналогичный эффект наблюдается при расширении вокруг разреженных пандусов : для подходящих термодинамических условий число Маха после пандуса может быть меньше, чем перед ним. ^[20] Напротив, в косых ударных волнах число Маха после удара может быть больше, чем до удара. ^[21]

Неклассический газодинамический режим

Наконец, жидкости с еще более высокой молекулярной сложностью могут демонстрировать неклассическое поведение в области однофазного пара вблизи насыщения. Их называют жидкостями Бете-Зельдовича-Томпсона (БЗТ), по имени физика Ганса Бете , ^[22] Yakov Zel'dovich , ^[23] и Филип Томпсон, ^[24]^[25] который первым работал с такими жидкостями.

Для термодинамических условий, лежащих в неклассическом режиме, немонотонная эволюция числа Маха в изэнтропических расширениях может быть обнаружена даже в дозвуковых условиях. Фактически, для значений $\Gamma <0$ , положительные значения $J$ может быть достигнута и в дозвуковых потоках ( $M<1$ ). Другими словами, немонотонная эволюция числа Маха возможна и в сужающемся сечении изэнтропического сопла. ^[25]

Более того, своеобразным явлением неклассического режима является так называемая обращенная газодинамика . В классическом режиме расширения представляют собой плавные изэнтропические процессы, а сжатия происходят за счет ударных волн , представляющих собой разрывы потока. Если обратить газовую динамику, происходит обратное: физически допустимы ударные волны разрежения, а сжатия происходят за счет плавных изэнтропических процессов. ^[24]

В результате отрицательного значения $\Gamma$ Для жидкостей BZT могут возникать еще два необычных явления: ударное расщепление и сложные волны. Расщепление ударной волны происходит, когда недопустимый разрыв давления развивается во времени за счет генерации двух более слабых ударных волн. ^[26]^[27] Вместо этого составные волны называются явлениями, в которых две элементарные волны распространяются как единое целое. ^[7]^[28]

Экспериментальных подтверждений неклассического газодинамического режима пока нет. Основными причинами являются сложность проведения экспериментов в таких сложных термодинамических условиях и термическая стабильность этих очень сложных молекул. ^[29]

Приложения

Сжимаемые течения в неидеальных условиях встречаются в ряде промышленных и аэрокосмических приложений. Они используются, например, в органических циклах Ренкина (ORC). ^[30] и системы со сверхкритическим диоксидом углерода (sCO ₂ ) ^[31] для производства электроэнергии . В аэрокосмической сфере жидкости в условиях, близких к насыщению, могут использоваться в качестве окислителей в гибридных ракетных двигателях или для поверхностного охлаждения сопел ракет . ^[32] Газы, состоящие из молекул с высокой молекулярной массой, можно использовать в сверхзвуковых аэродинамических трубах вместо воздуха для получения более высоких чисел Рейнольдса . ^[33] Наконец, неидеальные потоки находят применение при топлива высокоскоростной транспортировке _{и в быстром расширении сверхкритических растворов (RESS) CO 2} для генерации частиц или извлечения химических веществ. ^[34]

Органические циклы Ренкина

Обычные циклы Ренкина представляют собой термодинамические циклы , в которых вода используется в качестве рабочего тела для производства электроэнергии из тепловых источников. ^[36] В органических циклах Ренкина, напротив, вода заменяется молекулярно сложными органическими соединениями . Поскольку температура испарения этих видов жидкостей ниже, чем у воды при атмосферном давлении, можно использовать источники с низкой и средней температурой, позволяющие рекуперировать тепло , например, от биомассы сжигания , тепла промышленных отходов или геотермального тепла . ^[37] По этим причинам технология ORC относится к классу возобновляемых источников энергии .

При проектировании механических узлов, например турбин , работающих на установках ОРК, принципиальным является учет типичных неидеальных газодинамических явлений. Фактически однофазный пар на входе в статор турбины ORC обычно развивается в неидеальной термодинамической области вблизи кривой насыщения пар-жидкость и критической точки. Более того, из-за высокой молекулярной массы используемых сложных органических соединений скорость звука в этих жидкостях мала по сравнению со скоростью звука в воздухе и других простых газах. Следовательно, в статорах турбин весьма вероятно возникновение сверхзвуковых потоков, даже если достигаются довольно низкие скорости потока. ^[38] Высокие сверхзвуковые потоки могут вызывать большие потери и механические напряжения в лопатках турбины из-за возникновения ударных волн, вызывающих сильный подъем давления. ^[39] Однако при использовании рабочих жидкостей класса BZT характеристики детандера можно улучшить, используя некоторые неклассические явления. ^[40]^[41]

Сверхкритические циклы углекислого газа

Когда углекислый газ удерживается выше критического давления (73,773 бар) ^[42] и температура (30,9780 °С), ^[42] он может вести себя как газ, так и как жидкость, то есть он расширяется, полностью заполняя свой контейнер, как газ, но имеет плотность, аналогичную плотности жидкости.

Сверхкритический CO ₂ , химически стабилен очень дешев и негорюч , что делает его пригодным в качестве рабочей жидкости для транскритических циклов . ^[43] Например, он используется в бытовых водяных тепловых насосах , которые могут достигать высокой эффективности . ^[43]

Более того, при использовании на электростанциях, использующих циклы Брайтона и Ренкина, он может повысить эффективность и выходную мощность. Его высокая плотность позволяет значительно уменьшить габариты турбомашин, сохраняя при этом высокий КПД этих компонентов. Поэтому можно использовать более простые конструкции, в то время как паровые турбины требуют нескольких ступеней турбины, что неизбежно приводит к увеличению размеров и затрат. ^[44]

Напротив, механические компоненты в циклах Брайтона sCO ₂ , особенно турбомашины и теплообменники, страдают от коррозии . ^[45]

См. также

Ссылки

^ Каллен, Герберт Б. (1985). Термодинамика и введение в термостатистику (2-е изд.). Нью-Йорк: Дж. Уайли и сыновья. стр. 255–261. ISBN 978-0-471-86256-7 .
^ Шлоски, Кевин М. (1989). «Сверхкритические фазовые переходы при очень высоком давлении» . Журнал химического образования . 66 (12): 989. Бибкод : 1989ЖЧЭд..66..989С . дои : 10.1021/ed066p989 . ISSN 0021-9584 .
^ Фагри, Амир; Чжан, Ювэнь (1 января 2006 г.), Фагри, Амир; Чжан, Ювэнь (ред.), «Двухфазный поток и теплопередача» , «Явления переноса в многофазных системах» , Бостон: Academic Press, стр. 853–949, doi : 10.1016/b978-0-12-370610-2.50016-7 , ISBN 978-0-12-370610-2 , S2CID 98384899 , получено 6 июля 2023 г.
^ Jump up to: ^а ^б ^с Ваальс, Дж. Д. ван дер; Роулинсон, Джон Шипли (1988). О непрерывности газообразного и жидкого состояний . Исследования по статистической механике. Амстердам: Северная Голландия. ISBN 978-0-444-87077-3 .
^ Jump up to: ^а ^б ^с Колонна, П.; Гуардоне, А. (2006). «Молекулярная интерпретация неклассической газовой динамики плотных паров в рамках модели Ван-дер-Ваальса» . Физика жидкостей . 18 (5): 056101–056101–14. Бибкод : 2006PhFl...18e6101C . дои : 10.1063/1.2196095 . ISSN 1070-6631 .
^ Jump up to: ^а ^б ^с ^д ^и Томпсон, Филип А. (1972). Динамика сжимаемой жидкости . Передовая инженерная серия. Нью-Йорк: МакГроу-Хилл. стр. 76–99. ISBN 978-0-07-064405-2 .
^ Jump up to: ^а ^б Меникофф, Ральф; Плор, Брэдли Дж. (1 января 1989 г.). «Задача Римана для течения жидкости реальных материалов» . Обзоры современной физики . 61 (1): 75–130. Бибкод : 1989РвМП...61...75М . дои : 10.1103/revmodphys.61.75 . ISSN 0034-6861 .
^ Цукер, Роберт Д.; Библарц, Оскар (2002). Основы газовой динамики (2-е изд.). Хобокен, Нью-Джерси: Уайли. п. 327. ИСБН 978-0-471-05967-7 .
^ Томпсон, Филип А. (1972). Динамика сжимаемой жидкости . Передовая инженерная серия. Нью-Йорк: МакГроу-Хилл. стр. 99–101. ISBN 978-0-07-064405-2 .
^ Парсегян, В. Адриан (2005). Силы Ван дер Ваальса: Справочник для биологов, химиков, инженеров и физиков . Кембридж: Издательство Кембриджского университета. дои : 10.1017/cbo9780511614606 . ISBN 978-0-521-83906-8 .
^ Пэн, Дин-Юй; Робинсон, Дональд Б. (февраль 1976 г.). «Новое двухконстантное уравнение состояния» . Основы промышленной и инженерной химии . 15 (1): 59–64. дои : 10.1021/i160057a011 . ISSN 0196-4313 . S2CID 98225845 .
^ Спан, Р.; Вагнер, В. (1 января 2003 г.). «Уравнения состояния для технических приложений. I. Одновременно оптимизированные функциональные формы для неполярных и полярных жидкостей» . Международный журнал теплофизики . 24 (1): 1–39. дои : 10.1023/А:1022390430888 . ISSN 1572-9567 . S2CID 116961558 .
^ Спан, Роланд (2000), «Описание смесей с помощью многопараметрических уравнений состояния» , Многопараметрические уравнения состояния , Берлин, Гейдельберг: Springer Berlin Heidelberg, стр. 319–340, doi : 10.1007/978-3-662-04092-8_8 , ISBN 978-3-642-08671-7 , получено 5 июля 2023 г.
^ Белл, Ян Х.; Вронский, Йоррит; Куойлин, Сильвен; Леморт, Винсент (27 января 2014 г.). «Оценка теплофизических свойств чистых и псевдочистых жидкостей и открытая библиотека теплофизических свойств CoolProp» . Исследования в области промышленной и инженерной химии . 53 (6): 2498–2508. дои : 10.1021/ie4033999 . ISSN 0888-5885 . ПМЦ 3944605 . ПМИД 24623957 .
^ 1942, Ландау, Л.Д. «Об ударных волнах» J. Phys. СССР 6 229-230
^ Jump up to: ^а ^б Томпсон, Филип А. (1971). «Фундаментальная производная в газодинамике» . Физика жидкостей . 14 (9): 1843–1849. Бибкод : 1971PhFl...14.1843T . дои : 10.1063/1.1693693 . ISSN 0031-9171 .
^ Цянь, Сюэ-Шен (1946). «Одномерные потоки газа, характеризуемые уравнением состояния Вандера Ваала» . Журнал математики и физики . 25 (1–4): 301–324. дои : 10.1002/sapm1946251301 . ISSN 0097-1421 .
^ Jump up to: ^а ^б Клювик, Альфред (1 мая 2004 г.). «Внутренние течения плотных газов» . Акта Механика . 169 (1–4): 123–143. дои : 10.1007/s00707-004-0096-z . ISSN 0001-5970 . S2CID 121634296 .
^ Jump up to: ^а ^б ^с Крамер, MS; Бест, LM (1991). «Установившиеся изэнтропические течения плотных газов» . Физика жидкостей A: Гидродинамика . 3 (1): 219–226. Бибкод : 1991PhFlA...3..219C . дои : 10.1063/1.857855 . ISSN 0899-8213 .
^ Крамер, MS; Крикенбергер, AB (1992). «Функция Прандтля-Мейера для плотных газов» . Журнал АИАА . 30 (2): 561–564. Бибкод : 1992AIAAJ..30..561C . дои : 10.2514/3.10956 . ISSN 0001-1452 .
^ Вимеркати, Давиде; Гори, Джулио; Гуардоне, Альберто (21 мая 2018 г.). «Неидеальные косые ударные волны» . Журнал механики жидкости . 847 : 266–285. Бибкод : 2018JFM...847..266V . дои : 10.1017/jfm.2018.328 . hdl : 11311/1063005 . ISSN 0022-1120 . S2CID 125447693 .
^ Бете, Х.А. (1998), «К теории ударных волн для произвольного уравнения состояния» , Классические статьи по науке об ударном сжатии , Нью-Йорк, Нью-Йорк: Springer New York, стр. 421–495, doi : 10.1007/978- 1-4612-2218-7_11 , ISBN 978-1-4612-7461-2 , получено 5 июля 2023 г.
^ «14. О возможности ударных волн разрежения» , Избранные работы Якова Борисовича Зельдовича, Том I , Princeton University Press, стр. 152–154, 1992-12-31, doi : 10.1515/9781400862979.152 , ISBN 9781400862979 , получено 5 июля 2023 г.
^ Jump up to: ^а ^б Томпсон, Пенсильвания; Ламбракис, КЦ (21 августа 1973 г.). «Негативные ударные волны» . Журнал механики жидкости . 60 (1): 187–208. Бибкод : 1973JFM....60..187T . дои : 10.1017/s002211207300011x . ISSN 0022-1120 . S2CID 123608377 .
^ Jump up to: ^а ^б Ламбракис, Константин К. (1972). «Существование реальных жидкостей с отрицательной фундаментальной производной Γ» . Физика жидкостей . 15 (5): 933–935. Бибкод : 1972PhFl...15..933L . дои : 10.1063/1.1694004 . ISSN 0031-9171 .
^ Крамер, М.С. (февраль 1989 г.). «Ударное расщепление в однофазных газах» . Журнал механики жидкости . 199 : 281–296. Бибкод : 1989JFM...199..281C . дои : 10.1017/s0022112089000388 . ISSN 0022-1120 . S2CID 124690578 .
^ Крамер, MS (1991), «Неклассическая динамика классических газов» , Нелинейные волны в реальных жидкостях , Вена: Springer Vienna, стр. 91–145, doi : 10.1007/978-3-7091-2608-0_5 , ISBN 978-3-211-82277-7 , получено 5 июля 2023 г.
^ ЛЮВИК, АЛЬФРЕД (2001), «Удары разрежения» , Справочник по ударным волнам , Elsevier, стр. 339–411, doi : 10.1016/b978-012086430-0/50008-7 , ISBN 9780120864300
^ Борисов А.А.; Борисов, Ал. А.; Кутателадзе, С.С.; Накоряков В.Е. (январь 1983 г.). «Ударная волна разрежения вблизи критической точки жидкость–пар» . Журнал механики жидкости . 126 : 59–73. Бибкод : 1983JFM...126...59B . дои : 10.1017/s002211208300004x . ISSN 0022-1120 . S2CID 123399921 .
^ Анджелино, Г.; Инверницци, К.; Макки, Э. (1991), «Оптимизация органической рабочей жидкости для космических энергетических циклов» , Современные темы исследований в области аэрокосмических двигателей , Нью-Йорк, штат Нью-Йорк: Springer New York, стр. 297–326, номер документа : 10.1007/978-1-4612. -0945-4_16 , ISBN 978-1-4612-6956-4 , получено 5 июля 2023 г.
^ Фехер, Э.Г. (1968). «Сверхкритический термодинамический энергетический цикл» . Преобразование энергии . 8 (2): 85–90. дои : 10.1016/0013-7480(68)90105-8 . ISSN 0013-7480 .
^ «Элементы ракетного движения. 2-е издание. Джордж П. Саттон. J. Wiley and Sons Inc., Нью-Йорк, 1956. 483 стр. Иллюстрировано. 82 с» . Журнал Королевского авиационного общества . 61 (559): 503. 1957. doi : 10.1017/s0368393100128512 . ISSN 0368-3931 .
^ Санье, П.; Веран, Ж.-Л. (1998). «О валидации моделирования высокоэнтальпийной аэродинамической трубы» . Аэрокосмическая наука и технология . 2 (7): 425–437. дои : 10.1016/s1270-9638(99)80002-9 . ISSN 1270-9638 .
^ Хельфген, Б.; Тюрк, М.; Шабер, К. (2003). «Гидродинамическое и аэрозольное моделирование быстрого расширения сверхкритических растворов (RESS-процесс)» . Журнал сверхкритических жидкостей . 26 (3): 225–242. дои : 10.1016/s0896-8446(02)00159-6 . ISSN 0896-8446 .
^ Турунен-Саарешти, Теему; Ууситало, Антти; Хонкатукиа, Юха (2017). «Проектирование и испытания высокотемпературного испытательного стенда микро-ORC с использованием силоксана в качестве рабочей жидкости» . Физический журнал: серия конференций . 821 (1): 012024. Бибкод : 2017JPhCS.821a2024T . дои : 10.1088/1742-6596/821/1/012024 . ISSN 1742-6588 . S2CID 114806415 .
^ Сайто, ТС; Хоши, А. (2004). «Предлагаемая солнечная система с циклом Ренкина с паровым аккумулятором с фазовым переходом и солнечным коллектором CPC» . МЭКЕС '02. 2002 г. 37-я Межобщественная конференция по вопросам преобразования энергии, 2002 г. IEEE. стр. 725–730. дои : 10.1109/iecec.2002.1392137 . ISBN 0-7803-7296-4 . S2CID 110987716 .
^ Куойлин, Сильвен; Брук, Мартин Ван Ден; Деклей, Себастьен; Деваллеф, Пьер; Леморт, Винсент (2013). «Технико-экономическое обследование систем органического цикла Ренкина (ОРЦ)» . Обзоры возобновляемой и устойчивой энергетики . 22 : 168–186. дои : 10.1016/j.rser.2013.01.028 . ISSN 1364-0321 .
^ Браун, Брэди; Эргроу, Брайан (11 января 1999 г.). «Применение жидкостей Бете-Зельдовича-Томпсона в двигателях с органическим циклом Ренкина» . 37-е совещание и выставка по аэрокосмическим наукам . Рестон, Вириджина: Американский институт аэронавтики и астронавтики. дои : 10.2514/6.1999-462 .
^ Дентон, доктор медицинских наук; Сюй, Л. (4 июня 1989 г.). «Потеря задней кромки околозвуковых турбинных лопаток» . Материалы Международного конгресса и выставки газовых турбин и авиационных двигателей ASME 1989 г. Том 1: Турбомашины . Американское общество инженеров-механиков. дои : 10.1115/89-gt-278 . ISBN 978-0-7918-7913-9 . S2CID 111017969 .
^ Клювик, А. (1994), «Взаимодействующие ламинарные пограничные слои плотных газов» , Гидродинамика и газодинамика , Вена: Springer Vienna, стр. 335–349, doi : 10.1007/978-3-7091-9310-5_37 , ISBN 978-3-211-82495-5 , получено 6 июля 2023 г.
^ КРЕМЕР, М.С.; ПАРК, С. (1999). «О подавлении ударной сепарации в жидкостях Бете–Зельдовича–Томпсона» . Журнал механики жидкости . 393 (1): 1–21. Бибкод : 1999JFM...393....1C . дои : 10.1017/s0022112099005479 . ISSN 0022-1120 . S2CID 122254018 .
^ Jump up to: ^а ^б Спан, Роланд; Вагнер, Вольфганг (1 ноября 1996 г.). «Новое уравнение состояния углекислого газа, охватывающее область жидкости от температуры тройной точки до 1100 К при давлениях до 800 МПа» . Журнал физических и химических справочных данных . 25 (6): 1509–1596. дои : 10.1063/1.555991 . ISSN 0047-2689 .
^ Jump up to: ^а ^б Ма, Итай; Лю, Чжунъянь; Тянь, Хуа (2013). «Обзор транскритических углекислотных тепловых насосов и холодильных циклов» . Энергия . 55 : 156–172. дои : 10.1016/j.energy.2013.03.030 . ISSN 0360-5442 .
^ Флеминг, Дэррин; Паш, Джим; Конбой, Томас; Карлсон, Мэтт (3 июня 2013 г.). «Платформа для испытаний и план коммерциализации систем теплообмена для энергетических циклов SCO2» . Материалы ASME Turbo Expo 2013: Техническая конференция и выставка турбин. Том 8: Энергетические циклы сверхкритического CO2; ветроэнергетика; Почести и награды . Американское общество инженеров-механиков. дои : 10.1115/gt2013-95125 . ISBN 978-0-7918-5529-4 . ОСТИ 1115493 .
^ Флеминг, Дэррин; Круизенга, Алан; Паш, Джеймс; Конбой, Том; Карлсон, Мэтт (16 июня 2014 г.). «Коррозия и эрозия в сверхкритических энергетических циклах с CO2» . Материалы ASME Turbo Expo 2014: Техническая конференция и выставка турбин. Том 3B: Применение в нефтегазовой отрасли; Органические энергетические системы с циклом Ренкина; Сверхкритические энергетические циклы CO2; Ветроэнергетика . дои : 10.1115/gt2014-25136 . ISBN 978-0-7918-4566-0 . ОСТИ 1221554 .

Дальнейшее чтение

Андерсон, Джон Дэвид (2003). Современные сжимаемые течения: в исторической перспективе . МакГроу-Хилл.
ди Маре, Франческа; Спинелли, Андреа; Пини, Маттео (2018). Динамика неидеальной сжимаемой жидкости для движения и мощности . Спрингер Линк.
Фехер, Э.Г. (1968). «Сверхкритический термодинамический энергетический цикл» . Преобразование энергии . 8 (2): 85–90. дои : 10.1016/0013-7480(68)90105-8 .
Клювик, Альфред (2017). «Динамика неидеальной сжимаемой жидкости: вызов теории» . Журнал физики . 821 (1): 012001. Бибкод : 2017JPhCS.821a2001K . дои : 10.1088/1742-6596/821/1/012001 . S2CID 125325704 .
Макки, Эннио; Астольфи, Марко (2016). Энергетические системы органического цикла Ренкина (ORC) (1-е изд.). Эльзевир. ISBN 9780081005101 .

Внешние ссылки

[1] Каллен, Герберт Б. (1985). Термодинамика и введение в термостатистику (2-е изд.). Нью-Йорк: Дж. Уайли и сыновья. стр. 255–261. ISBN 978-0-471-86256-7 .

[2] Шлоски, Кевин М. (1989). «Сверхкритические фазовые переходы при очень высоком давлении» . Журнал химического образования . 66 (12): 989. Бибкод : 1989ЖЧЭд..66..989С . дои : 10.1021/ed066p989 . ISSN 0021-9584 .

[3] Фагри, Амир; Чжан, Ювэнь (1 января 2006 г.), Фагри, Амир; Чжан, Ювэнь (ред.), «Двухфазный поток и теплопередача» , «Явления переноса в многофазных системах» , Бостон: Academic Press, стр. 853–949, doi : 10.1016/b978-0-12-370610-2.50016-7 , ISBN 978-0-12-370610-2 , S2CID 98384899 , получено 6 июля 2023 г.

[:0-4] Jump up to: ^а ^б ^с Ваальс, Дж. Д. ван дер; Роулинсон, Джон Шипли (1988). О непрерывности газообразного и жидкого состояний . Исследования по статистической механике. Амстердам: Северная Голландия. ISBN 978-0-444-87077-3 .

[:3-5] Jump up to: ^а ^б ^с Колонна, П.; Гуардоне, А. (2006). «Молекулярная интерпретация неклассической газовой динамики плотных паров в рамках модели Ван-дер-Ваальса» . Физика жидкостей . 18 (5): 056101–056101–14. Бибкод : 2006PhFl...18e6101C . дои : 10.1063/1.2196095 . ISSN 1070-6631 .

[:4-6] Jump up to: ^а ^б ^с ^д ^и Томпсон, Филип А. (1972). Динамика сжимаемой жидкости . Передовая инженерная серия. Нью-Йорк: МакГроу-Хилл. стр. 76–99. ISBN 978-0-07-064405-2 .

[:1-7] Jump up to: ^а ^б Меникофф, Ральф; Плор, Брэдли Дж. (1 января 1989 г.). «Задача Римана для течения жидкости реальных материалов» . Обзоры современной физики . 61 (1): 75–130. Бибкод : 1989РвМП...61...75М . дои : 10.1103/revmodphys.61.75 . ISSN 0034-6861 .

[8] Цукер, Роберт Д.; Библарц, Оскар (2002). Основы газовой динамики (2-е изд.). Хобокен, Нью-Джерси: Уайли. п. 327. ИСБН 978-0-471-05967-7 .

[9] Томпсон, Филип А. (1972). Динамика сжимаемой жидкости . Передовая инженерная серия. Нью-Йорк: МакГроу-Хилл. стр. 99–101. ISBN 978-0-07-064405-2 .

[10] Парсегян, В. Адриан (2005). Силы Ван дер Ваальса: Справочник для биологов, химиков, инженеров и физиков . Кембридж: Издательство Кембриджского университета. дои : 10.1017/cbo9780511614606 . ISBN 978-0-521-83906-8 .

[11] Пэн, Дин-Юй; Робинсон, Дональд Б. (февраль 1976 г.). «Новое двухконстантное уравнение состояния» . Основы промышленной и инженерной химии . 15 (1): 59–64. дои : 10.1021/i160057a011 . ISSN 0196-4313 . S2CID 98225845 .

[12] Спан, Р.; Вагнер, В. (1 января 2003 г.). «Уравнения состояния для технических приложений. I. Одновременно оптимизированные функциональные формы для неполярных и полярных жидкостей» . Международный журнал теплофизики . 24 (1): 1–39. дои : 10.1023/А:1022390430888 . ISSN 1572-9567 . S2CID 116961558 .

[13] Спан, Роланд (2000), «Описание смесей с помощью многопараметрических уравнений состояния» , Многопараметрические уравнения состояния , Берлин, Гейдельберг: Springer Berlin Heidelberg, стр. 319–340, doi : 10.1007/978-3-662-04092-8_8 , ISBN 978-3-642-08671-7 , получено 5 июля 2023 г.

[:5-14] Белл, Ян Х.; Вронский, Йоррит; Куойлин, Сильвен; Леморт, Винсент (27 января 2014 г.). «Оценка теплофизических свойств чистых и псевдочистых жидкостей и открытая библиотека теплофизических свойств CoolProp» . Исследования в области промышленной и инженерной химии . 53 (6): 2498–2508. дои : 10.1021/ie4033999 . ISSN 0888-5885 . ПМЦ 3944605 . ПМИД 24623957 .

[15] 1942, Ландау, Л.Д. «Об ударных волнах» J. Phys. СССР 6 229-230

[:6-16] Jump up to: ^а ^б Томпсон, Филип А. (1971). «Фундаментальная производная в газодинамике» . Физика жидкостей . 14 (9): 1843–1849. Бибкод : 1971PhFl...14.1843T . дои : 10.1063/1.1693693 . ISSN 0031-9171 .

[17] Цянь, Сюэ-Шен (1946). «Одномерные потоки газа, характеризуемые уравнением состояния Вандера Ваала» . Журнал математики и физики . 25 (1–4): 301–324. дои : 10.1002/sapm1946251301 . ISSN 0097-1421 .

[:7-18] Jump up to: ^а ^б Клювик, Альфред (1 мая 2004 г.). «Внутренние течения плотных газов» . Акта Механика . 169 (1–4): 123–143. дои : 10.1007/s00707-004-0096-z . ISSN 0001-5970 . S2CID 121634296 .

[:8-19] Jump up to: ^а ^б ^с Крамер, MS; Бест, LM (1991). «Установившиеся изэнтропические течения плотных газов» . Физика жидкостей A: Гидродинамика . 3 (1): 219–226. Бибкод : 1991PhFlA...3..219C . дои : 10.1063/1.857855 . ISSN 0899-8213 .

[20] Крамер, MS; Крикенбергер, AB (1992). «Функция Прандтля-Мейера для плотных газов» . Журнал АИАА . 30 (2): 561–564. Бибкод : 1992AIAAJ..30..561C . дои : 10.2514/3.10956 . ISSN 0001-1452 .

[21] Вимеркати, Давиде; Гори, Джулио; Гуардоне, Альберто (21 мая 2018 г.). «Неидеальные косые ударные волны» . Журнал механики жидкости . 847 : 266–285. Бибкод : 2018JFM...847..266V . дои : 10.1017/jfm.2018.328 . hdl : 11311/1063005 . ISSN 0022-1120 . S2CID 125447693 .

[22] Бете, Х.А. (1998), «К теории ударных волн для произвольного уравнения состояния» , Классические статьи по науке об ударном сжатии , Нью-Йорк, Нью-Йорк: Springer New York, стр. 421–495, doi : 10.1007/978- 1-4612-2218-7_11 , ISBN 978-1-4612-7461-2 , получено 5 июля 2023 г.

[23] «14. О возможности ударных волн разрежения» , Избранные работы Якова Борисовича Зельдовича, Том I , Princeton University Press, стр. 152–154, 1992-12-31, doi : 10.1515/9781400862979.152 , ISBN 9781400862979 , получено 5 июля 2023 г.

[:2-24] Jump up to: ^а ^б Томпсон, Пенсильвания; Ламбракис, КЦ (21 августа 1973 г.). «Негативные ударные волны» . Журнал механики жидкости . 60 (1): 187–208. Бибкод : 1973JFM....60..187T . дои : 10.1017/s002211207300011x . ISSN 0022-1120 . S2CID 123608377 .

[:9-25] Jump up to: ^а ^б Ламбракис, Константин К. (1972). «Существование реальных жидкостей с отрицательной фундаментальной производной Γ» . Физика жидкостей . 15 (5): 933–935. Бибкод : 1972PhFl...15..933L . дои : 10.1063/1.1694004 . ISSN 0031-9171 .

[26] Крамер, М.С. (февраль 1989 г.). «Ударное расщепление в однофазных газах» . Журнал механики жидкости . 199 : 281–296. Бибкод : 1989JFM...199..281C . дои : 10.1017/s0022112089000388 . ISSN 0022-1120 . S2CID 124690578 .

[27] Крамер, MS (1991), «Неклассическая динамика классических газов» , Нелинейные волны в реальных жидкостях , Вена: Springer Vienna, стр. 91–145, doi : 10.1007/978-3-7091-2608-0_5 , ISBN 978-3-211-82277-7 , получено 5 июля 2023 г.

[28] ЛЮВИК, АЛЬФРЕД (2001), «Удары разрежения» , Справочник по ударным волнам , Elsevier, стр. 339–411, doi : 10.1016/b978-012086430-0/50008-7 , ISBN 9780120864300

[29] Борисов А.А.; Борисов, Ал. А.; Кутателадзе, С.С.; Накоряков В.Е. (январь 1983 г.). «Ударная волна разрежения вблизи критической точки жидкость–пар» . Журнал механики жидкости . 126 : 59–73. Бибкод : 1983JFM...126...59B . дои : 10.1017/s002211208300004x . ISSN 0022-1120 . S2CID 123399921 .

[30] Анджелино, Г.; Инверницци, К.; Макки, Э. (1991), «Оптимизация органической рабочей жидкости для космических энергетических циклов» , Современные темы исследований в области аэрокосмических двигателей , Нью-Йорк, штат Нью-Йорк: Springer New York, стр. 297–326, номер документа : 10.1007/978-1-4612. -0945-4_16 , ISBN 978-1-4612-6956-4 , получено 5 июля 2023 г.

[31] Фехер, Э.Г. (1968). «Сверхкритический термодинамический энергетический цикл» . Преобразование энергии . 8 (2): 85–90. дои : 10.1016/0013-7480(68)90105-8 . ISSN 0013-7480 .

[32] «Элементы ракетного движения. 2-е издание. Джордж П. Саттон. J. Wiley and Sons Inc., Нью-Йорк, 1956. 483 стр. Иллюстрировано. 82 с» . Журнал Королевского авиационного общества . 61 (559): 503. 1957. doi : 10.1017/s0368393100128512 . ISSN 0368-3931 .

[33] Санье, П.; Веран, Ж.-Л. (1998). «О валидации моделирования высокоэнтальпийной аэродинамической трубы» . Аэрокосмическая наука и технология . 2 (7): 425–437. дои : 10.1016/s1270-9638(99)80002-9 . ISSN 1270-9638 .

[34] Хельфген, Б.; Тюрк, М.; Шабер, К. (2003). «Гидродинамическое и аэрозольное моделирование быстрого расширения сверхкритических растворов (RESS-процесс)» . Журнал сверхкритических жидкостей . 26 (3): 225–242. дои : 10.1016/s0896-8446(02)00159-6 . ISSN 0896-8446 .

[35] Турунен-Саарешти, Теему; Ууситало, Антти; Хонкатукиа, Юха (2017). «Проектирование и испытания высокотемпературного испытательного стенда микро-ORC с использованием силоксана в качестве рабочей жидкости» . Физический журнал: серия конференций . 821 (1): 012024. Бибкод : 2017JPhCS.821a2024T . дои : 10.1088/1742-6596/821/1/012024 . ISSN 1742-6588 . S2CID 114806415 .

[36] Сайто, ТС; Хоши, А. (2004). «Предлагаемая солнечная система с циклом Ренкина с паровым аккумулятором с фазовым переходом и солнечным коллектором CPC» . МЭКЕС '02. 2002 г. 37-я Межобщественная конференция по вопросам преобразования энергии, 2002 г. IEEE. стр. 725–730. дои : 10.1109/iecec.2002.1392137 . ISBN 0-7803-7296-4 . S2CID 110987716 .

[37] Куойлин, Сильвен; Брук, Мартин Ван Ден; Деклей, Себастьен; Деваллеф, Пьер; Леморт, Винсент (2013). «Технико-экономическое обследование систем органического цикла Ренкина (ОРЦ)» . Обзоры возобновляемой и устойчивой энергетики . 22 : 168–186. дои : 10.1016/j.rser.2013.01.028 . ISSN 1364-0321 .

[38] Браун, Брэди; Эргроу, Брайан (11 января 1999 г.). «Применение жидкостей Бете-Зельдовича-Томпсона в двигателях с органическим циклом Ренкина» . 37-е совещание и выставка по аэрокосмическим наукам . Рестон, Вириджина: Американский институт аэронавтики и астронавтики. дои : 10.2514/6.1999-462 .

[39] Дентон, доктор медицинских наук; Сюй, Л. (4 июня 1989 г.). «Потеря задней кромки околозвуковых турбинных лопаток» . Материалы Международного конгресса и выставки газовых турбин и авиационных двигателей ASME 1989 г. Том 1: Турбомашины . Американское общество инженеров-механиков. дои : 10.1115/89-gt-278 . ISBN 978-0-7918-7913-9 . S2CID 111017969 .

[40] Клювик, А. (1994), «Взаимодействующие ламинарные пограничные слои плотных газов» , Гидродинамика и газодинамика , Вена: Springer Vienna, стр. 335–349, doi : 10.1007/978-3-7091-9310-5_37 , ISBN 978-3-211-82495-5 , получено 6 июля 2023 г.

[41] КРЕМЕР, М.С.; ПАРК, С. (1999). «О подавлении ударной сепарации в жидкостях Бете–Зельдовича–Томпсона» . Журнал механики жидкости . 393 (1): 1–21. Бибкод : 1999JFM...393....1C . дои : 10.1017/s0022112099005479 . ISSN 0022-1120 . S2CID 122254018 .

[:10-42] Jump up to: ^а ^б Спан, Роланд; Вагнер, Вольфганг (1 ноября 1996 г.). «Новое уравнение состояния углекислого газа, охватывающее область жидкости от температуры тройной точки до 1100 К при давлениях до 800 МПа» . Журнал физических и химических справочных данных . 25 (6): 1509–1596. дои : 10.1063/1.555991 . ISSN 0047-2689 .

[:11-43] Jump up to: ^а ^б Ма, Итай; Лю, Чжунъянь; Тянь, Хуа (2013). «Обзор транскритических углекислотных тепловых насосов и холодильных циклов» . Энергия . 55 : 156–172. дои : 10.1016/j.energy.2013.03.030 . ISSN 0360-5442 .

[44] Флеминг, Дэррин; Паш, Джим; Конбой, Томас; Карлсон, Мэтт (3 июня 2013 г.). «Платформа для испытаний и план коммерциализации систем теплообмена для энергетических циклов SCO2» . Материалы ASME Turbo Expo 2013: Техническая конференция и выставка турбин. Том 8: Энергетические циклы сверхкритического CO2; ветроэнергетика; Почести и награды . Американское общество инженеров-механиков. дои : 10.1115/gt2013-95125 . ISBN 978-0-7918-5529-4 . ОСТИ 1115493 .

[45] Флеминг, Дэррин; Круизенга, Алан; Паш, Джеймс; Конбой, Том; Карлсон, Мэтт (16 июня 2014 г.). «Коррозия и эрозия в сверхкритических энергетических циклах с CO2» . Материалы ASME Turbo Expo 2014: Техническая конференция и выставка турбин. Том 3B: Применение в нефтегазовой отрасли; Органические энергетические системы с циклом Ренкина; Сверхкритические энергетические циклы CO2; Ветроэнергетика . дои : 10.1115/gt2014-25136 . ISBN 978-0-7918-4566-0 . ОСТИ 1221554 .

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

[30]

[31]

[32]

[33]

[34]

[35]

[36]

[37]

[38]

[39]

[40]

[41]

[42]

[43]

[44]

[45]