Биологическое малоугловое рассеяние

Схематическое изображение эксперимента SAS: кривые рассеяния раствора приводят к грубым структурам, в которые можно встроить более тонкие модели, чтобы выявить детали сборки.

Охват диапазона разрешения SAXS по сравнению с другими методами определения структуры

Биологическое малоугловое рассеяние - это метод малоуглового рассеяния для анализа структуры биологических материалов. Малоугловое рассеяние используется для изучения структуры различных объектов, таких как растворы биологических макромолекул, нанокомпозиты, сплавы и синтетические полимеры. Малоугловое рассеяние рентгеновских лучей ( SAXS ) и малоугловое рассеяние нейтронов ( SANS ) — это два взаимодополняющих метода, известные под общим названием малоугловое рассеяние (SAS). SAS — это метод, аналогичный дифракции рентгеновских лучей и нейтронов , широкоугольному рассеянию рентгеновских лучей , а также статическому рассеянию света . В отличие от других методов рассеяния рентгеновских лучей и нейтронов, SAS дает информацию о размерах и форме как кристаллических, так и некристаллических частиц. При исследовании биологических материалов, которые очень часто находятся в водных растворах, картина рассеяния является ориентационно-усредненной.

Шаблоны SAS собираются под небольшими углами в несколько градусов. SAS способен передавать структурную информацию в диапазоне разрешения от 1 до 25 нм , а также о расстояниях повторения в частично упорядоченных системах размером до 150 нм. Сверхмалое угловое рассеяние (USAS) может разрешить даже большие размеры. ( Малоугловое рассеяние скользящего падения GISAS) — мощный метод изучения слоев биологических молекул на поверхностях.

В биологических приложениях SAS используется для определения структуры частицы с точки зрения среднего размера и формы частиц. Также можно получить информацию об отношении поверхности к объему . Обычно биологические макромолекулы диспергированы в жидкости. Метод является точным, в основном неразрушающим и обычно требует лишь минимальной подготовки проб. Однако биологические молекулы всегда подвержены радиационному повреждению .

По сравнению с другими методами определения структуры, такими как ЯМР раствора или рентгеновская кристаллография , SAS позволяет преодолеть некоторые ограничения. Например, ЯМР раствора ограничен размером белка, тогда как SAS можно использовать как для небольших молекул, так и для больших мультимолекулярных ансамблей. ЯМР твердого тела по-прежнему является незаменимым инструментом для определения информации на атомном уровне макромолекул размером более 40 кДа или некристаллических образцов, таких как амилоидные фибриллы. Определение структуры методом рентгеновской кристаллографии может занять несколько недель или даже лет, тогда как измерения SAS занимают дни. SAS также можно сочетать с другими аналитическими методами, такими как эксклюзионная хроматография, для изучения гетерогенных образцов. Однако с помощью SAS невозможно измерить положение атомов внутри молекулы.

Метод

Кривые рассеяния рентгеновских лучей в растворе, рассчитанные на основе атомных моделей двадцати пяти различных белков с молекулярной массой от 10 до 300 кДа.

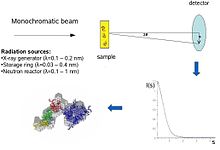
Концептуально эксперименты по малоугловому рассеянию просты: образец подвергается воздействию рентгеновских лучей или нейтронов , а рассеянное излучение регистрируется детектором. Поскольку измерения SAS выполняются очень близко к первичному лучу («малые углы»), для этого метода требуется сильно коллимированный или сфокусированный рентгеновский или нейтронный луч. Биологическое малоугловое рассеяние рентгеновских лучей часто проводят на источниках синхротронного излучения , поскольку биологические молекулы обычно рассеиваются слабо и измеряемые растворы разбавлены . Биологический метод SAXS основан на высокой интенсивности пучков рентгеновских фотонов, обеспечиваемых синхротронными накопителями . Кривая рассеяния рентгеновских лучей или нейтронов ( интенсивность в зависимости от угла рассеяния ) используется для создания модели белка с низким разрешением, показанной здесь, на правом рисунке. Далее можно использовать данные рассеяния рентгеновских лучей или нейтронов и поместить отдельные домены (рентгеновские или ЯМР- структуры) в «оболочку SAXS».

В эксперименте по рассеянию раствор макромолекул подвергается воздействию рентгеновских лучей (с длиной волны λ обычно около 0,15 нм) или тепловых нейтронов ( λ ≈ 0,5 нм). Рассеянная интенсивность I(s) регистрируется как функция переданного импульса s ( s=4πsinθ/λ , где 2θ — угол между падающим и рассеянным излучением). Из интенсивности раствора вычитают рассеяние только от растворителя. Случайные положения и ориентации частиц приводят к изотропному распределению интенсивности, которое для монодисперсных невзаимодействующих частиц пропорционально рассеянию от одной частицы, усредненному по всем ориентациям. Чистое рассеяние частиц пропорционально квадрату разницы плотности длины рассеяния ( электронная плотность для рентгеновских лучей и ядерная/спиновая плотность для нейтронов) между частицей и растворителем – так называемый контраст. Контраст можно варьировать путем рассеяния нейтронов с использованием смесей H ₂ O/ D ₂ O или селективного дейтерирования для получения дополнительной информации. Информативность данных SAS проиллюстрирована здесь на рисунке справа, на котором показаны картины рассеяния рентгеновских лучей от белков с разными складками и молекулярными массами . При малых углах (разрешение 2-3 нм) кривые представляют собой быстро затухающие функции s , существенно определяемые формой частиц, которые явно различаются. При среднем разрешении (от 2 до 0,5 нм) различия уже менее выражены, а при разрешении выше 0,5 нм все кривые очень похожи. Таким образом, SAS содержит информацию об общих структурных особенностях – форме, четвертичной и третичной структуре – но не подходит для анализа атомной структуры.

История

Первые применения относятся к концу 1930-х годов, когда основные принципы SAXS были разработаны в фундаментальной работе Гинье, последовавшей за его исследованиями металлических сплавов. В первой монографии Гинье и Фурне по МУРЭ уже было показано, что этот метод дает информацию не только о размерах и форме частиц, но и о внутренней структуре неупорядоченных и частично упорядоченных систем.

В 1960-е годы этот метод стал приобретать все большее значение при изучении биологических макромолекул в растворах, поскольку позволял получать структурную информацию с низким разрешением об общей форме и внутренней структуре в отсутствие кристаллов. Прорыв в экспериментах SAXS и SANS произошел в 1970-х годах благодаря наличию синхротронного излучения и источников нейтронов, причем последние открыли путь к изменению контраста путем замены растворителя H ₂ O на D ₂ O и специфических методов дейтерирования. Стало понятно, что исследования рассеяния на растворе при минимальных затратах времени и усилий дают полезную информацию о структуре некристаллических биохимических систем. Более того, SAXS/SANS также сделал возможным исследование в реальном времени межмолекулярных взаимодействий, включая сборку и крупномасштабные конформационные изменения в макромолекулярных ансамблях .

Основная трудность SAS как структурного метода заключается в извлечении трехмерной структурной информации объекта из одномерных экспериментальных данных. Раньше непосредственно из экспериментальных данных определялись только общие параметры частиц (например, объем, радиус вращения) макромолекул, тогда как анализ с использованием трехмерных моделей ограничивался простыми геометрическими телами (например, эллипсоидами, цилиндрами и т. д.). .) или выполнялось на основе метода проб и ошибок. Электронная микроскопия часто использовалась в качестве ограничения при построении консенсусных моделей. В 1980-х годах прогресс в других структурных методах привел к падению интереса биохимиков к исследованиям SAS, которые делали структурные выводы всего лишь на основе нескольких общих параметров или основывались на моделях проб и ошибок.

1990-е годы принесли прорыв в методах анализа данных SAXS/SANS, который открыл путь к надежному ab initio моделированию макромолекулярных комплексов, включая детальное определение формы и доменной структуры, а также применение методов уточнения твердого тела. Этот прогресс сопровождался дальнейшим развитием аппаратуры, позволяющей достигать временного разрешения менее миллисекунды на источниках СИ третьего поколения при исследованиях сворачивания белков и нуклеиновых кислот.

В 2005 году стартовал четырехлетний проект. малоугловому по рентгеновских рассеянию лучей данных Инициатива для Европы объемов . (SAXIER) с целью объединить методы SAXS с другими аналитическими методами и создать автоматизированное программное обеспечение для быстрого анализа больших В рамках проекта была создана единая европейская инфраструктура SAXS с использованием самых передовых доступных методов.

Анализ данных

В эксперименте SAS хорошего качества измеряются несколько растворов с разными концентрациями исследуемой макромолекулы. Экстраполируя кривые рассеяния, измеренные при различных концентрациях, до нулевой концентрации, можно получить кривую рассеяния, которая представляет бесконечное разбавление. Тогда эффекты концентрации не должны влиять на кривую рассеяния. Анализ данных экстраполированной кривой рассеяния начинается с проверки начала кривой рассеяния в области около s = 0 . Если регион соответствует приближению Гинье (также известному как закон Гинье ), выборка не агрегируется . Тогда форму рассматриваемой частицы можно определить различными методами, некоторые из которых описаны в следующей ссылке.

Косвенное преобразование Фурье

Первым шагом обычно является вычисление преобразования Фурье кривой рассеяния. Преобразованную кривую можно интерпретировать как функцию распределения по расстояниям внутри частицы. Это преобразование также дает преимущество регуляризации входных данных.

Модели с низким разрешением

Модели лизоцима, построенные разными методами. Слева - общий вид, реконструированный САШОЙ ; посередине — модель фиктивного остатка, построенная DAMMIN ; ДАММИФ ; совместимая с правой цепью GASBOR, Модель

Одной из проблем анализа данных SAS является получение трехмерной структуры из одномерной картины рассеяния. Данные SAS не предполагают единого решения. Например, многие разные белки могут иметь одну и ту же кривую рассеяния. Реконструкция 3D-структуры может привести к созданию большого количества различных моделей. Чтобы избежать этой проблемы, необходимо принять во внимание ряд упрощений.

Дополнительный подход заключается в объединении данных и модели малоуглового рентгеновского и нейтронного рассеяния с программой MONSA.

интенсивно разрабатываются свободно доступные компьютерные программы для анализа SAS В EMBL . В первом общем ab initio подходе угловая огибающая частицы r=F(ω) , где ( r,ω ) — сферические координаты, описывается рядом сферических гармоник . Таким образом, форма низкого разрешения определяется несколькими параметрами – коэффициентами этого ряда – которые соответствуют данным рассеяния. Подход получил дальнейшее развитие и был реализован в компьютерной программе SASHA ( Small Angle Scattering Shape Determination ). Было продемонстрировано, что при определенных обстоятельствах из данных рассеяния можно выделить уникальную огибающую. Этот метод применим только к глобулярным частицам относительно простой формы и без значительных внутренних полостей. Чтобы преодолеть эти ограничения, был разработан другой подход, использующий различные типы поиска Монте-Карло. DALAI_GA — элегантная программа, которая берет сферу диаметром, равным максимальному размеру частиц Dmax, который определяется из данных рассеяния, и заполняет ее шариками. Каждая бусина принадлежит либо частице (индекс=1), либо растворителю (индекс=0). Таким образом, форма описывается двоичной строкой длины M. Начиная со случайной строки, генетический алгоритм ищет модель, соответствующую данным. При поиске, реализованном в программе DAMMIN , накладываются ограничения на компактность и связность . Если симметрия частицы известна, САША и ДАММИН могут использовать ее в качестве полезных ограничений. Процедура «дай-бери» SAXS3D и программа SASMODEL , основанная на взаимосвязанных эллипсоидах, представляют собой ab initio подходы Монте-Карло без ограничений в пространстве поиска.

Подход, который использует ансамбль фиктивных остатков (DR) и моделирует отжиг для построения локально «цепочесовместимой» DR-модели внутри сферы диаметром Dmax, позволяет извлечь больше деталей из данных SAXS. Этот метод реализован в программе GASBOR .

Картина рассеяния раствора многодоменных белков и макромолекулярных комплексов также может быть подобрана с использованием моделей, построенных на основе структур высокого разрешения ( ЯМР или рентгеновские лучи ) отдельных доменов или субъединиц при условии, что их третичная структура сохранена. В зависимости от сложности объекта применяются разные подходы для глобального поиска оптимальной конфигурации субъединиц, соответствующей экспериментальным данным.

Консенсусная модель

Модели, основанные на методе Монте-Карло, содержат сотни или тысячи параметров, поэтому необходимо проявлять осторожность, чтобы избежать чрезмерной интерпретации. Распространенный подход заключается в согласовании набора моделей, полученных в результате независимых прогонов реконструкции формы, для получения средней модели, сохраняющей наиболее устойчивые и, возможно, также наиболее надежные функции (например, с использованием программы SUPCOMB ).

Добавление недостающих петель

Неупорядоченные поверхностные аминокислоты (« петли ») часто не наблюдаются при ЯМР и кристаллографических исследованиях и могут отсутствовать в известных моделях. Такие неупорядоченные элементы вносят вклад в интенсивность рассеяния, и их вероятные местоположения можно найти, зафиксировав известную часть структуры и добавив недостающие части, чтобы соответствовать картине SAS всей частицы. Подход Dummy Residue был расширен и алгоритмы добавления недостающих петель или доменов были реализованы в программном комплексе CREDO .

Гибридные методы

Недавно было предложено несколько методов, использующих данные SAXS в качестве ограничений. Авторы стремились улучшить результаты распознавания складок. и предсказание структуры белка de novo методы. Данные SAXS обеспечивают преобразование Фурье гистограммы расстояний пар атомов (функция распределения пар) для данного белка. Это может служить структурным ограничением для методов, используемых для определения нативной конформационной складки белка. Распознавание нитей или складок предполагает, что трехмерная структура более консервативна, чем последовательность. Таким образом, очень расходящиеся последовательности могут иметь сходную структуру. С другой стороны, методы ab initio решают одну из самых больших проблем молекулярной биологии, а именно: предсказать сворачивание белка «с нуля», не используя гомологичных последовательностей или структур. Используя «фильтр SAXS», авторы смогли значительно очистить набор моделей белков de novo. Это было дополнительно подтверждено поиском структурной гомологии . Также было показано, что сочетание оценок SAXS с оценками, используемыми в методах многопоточности, значительно улучшает производительность распознавания складок. На одном примере было продемонстрировано, как приблизительная третичная структура модульных белков может быть собрана из структур доменов ЯМР высокого разрешения с использованием данных SAXS, ограничивающих трансляционные степени свободы. Другой пример показывает, как данные SAXS можно объединить с ЯМР, рентгеновской кристаллографией и электронной микроскопией для реконструкции четвертичной структуры многодоменного белка.

Гибкие системы

См. Также: Динамика белковых доменов.

Недавно был предложен элегантный метод решения проблемы внутренне неупорядоченных или многодоменных белков с гибкими линкерами . Это позволяет сосуществовать различные конформации белка, которые вместе вносят вклад в среднюю экспериментальную картину рассеяния. Первоначально EOM (метод оптимизации ансамбля) генерирует пул моделей, охватывающий пространство конфигурации белка. Затем для каждой модели рассчитывается кривая рассеяния. На втором этапе программа выбирает подмножества моделей белков. Среднее экспериментальное рассеяние рассчитывается для каждого подмножества и подгоняется к экспериментальным данным SAXS. Если наилучшее соответствие не найдено, модели перетасовываются между различными подмножествами и выполняется новый расчет среднего рассеяния и подгонка к экспериментальным данным. Этот метод был протестирован на двух белках – денатурированном лизоциме Брутона и протеинкиназе . Это дало некоторые интересные и многообещающие результаты.

Слои биологических молекул и GISAS

Покрытия биомолекул можно изучать с помощью рентгеновских лучей скользящего падения и рассеяния нейтронов. IsGISAXS ( малоугловое рассеяние рентгеновских лучей при скользящем падении ) — это программное обеспечение, предназначенное для моделирования и анализа GISAXS из наноструктур. IsGISAXS охватывает только рассеяние частицами нанометрового размера, которые похоронены в недрах матрицы, закреплены на подложке или похоронены тонким слоем на подложке. Также рассматривается случай с отверстиями. Геометрия ограничена плоскостью частиц. Сечение рассеяния разлагается по интерференционной функции и форм-фактору частицы . Акцент делается на скользящей геометрии падения, которая вызывает «эффект преломления луча». Форм-фактор частицы рассчитывается в рамках борновского приближения искаженной волны (DWBA), начиная с невозмущенного состояния с острыми границами раздела или с фактического перпендикулярного профиля показателя преломления . Доступны различные виды простых геометрических форм с полным учетом распределения размеров и форм в приближении развязки (DA), в локальном монодисперсном приближении (LMA), а также в приближении корреляции между размерами (SSCA). Обе - неупорядоченные системы частиц, определяемые их парой частица-частица. рассматриваются корреляционная функция и двумерный кристалл или паракристалл.

См. также

• Антон Паар
• Пользователь
• Электронная микроскопия
• Флуктуационное рентгеновское рассеяние (FXS)
• Малоугловое рассеяние рентгеновских лучей со скользящим падением ( GISAXS )
• Гомологическое моделирование
• Нейтронное спиновое эхо
• Банк данных по белкам
• Динамика белка
• Складывание белка
• Белковая нить
• Ригаку
• Розетта@дома
• Рентгеновская кристаллография

Ссылки

Дальнейшее чтение

• Кох М.Х., Вачетт П., Свергун Д.И. (май 2003 г.). «Малоугловое рассеяние: взгляд на свойства, структуру и структурные изменения биологических макромолекул в растворе». Ежеквартальные обзоры биофизики . 36 (2): 147–227. дои : 10.1017/S0033583503003871 . ПМИД   14686102 . S2CID   5432509 .
• Петухов М.В., Свергун Д.И. (август 2005 г.). «Глобальное моделирование макромолекулярных комплексов твердым телом на основе данных малоуглового рассеяния» . Биофизический журнал . 89 (2): 1237–50. Бибкод : 2005BpJ....89.1237P . дои : 10.1529/biophysj.105.064154 . ПМК   1366608 . ПМИД   15923225 .
• Бернадо П., Блэкледж М. (декабрь 2010 г.). «Структурная биология: Белки в динамическом равновесии» . Природа . 468 (7327): 1046–8. Бибкод : 2010Natur.468.1046B . дои : 10.1038/4681046а . ПМИД   21179158 .

Внешние ссылки

• SAXS/WAXS Beamline Австралийский синхротрон , Мельбурн, Австралия
• SIBYLS – линия луча в Advanced Light Source , Беркли, США
• SAXS – линия луча в Лаборатории синхротронного света ELETTRA , Триест, Италия
• X33 – линия луча в DESY , Гамбург, Германия
• Д11А – линия луча в Бразильской лаборатории синхротронного света , Кампинас, Бразилия
• X21 и X9 – линии луча национального источника синхротронного света в Брукхейвенской национальной лаборатории , Аптон, США.
• F2 и G1 – линии луча в Корнельской лаборатории ускорительных наук и образования , Итака, США
• Bio-SANS – линия луча в изотопном реакторе с высоким потоком в Национальной лаборатории Ок-Ридж , Ок-Ридж, Теннесси, США