Волатильная улыбка
Улыбки волатильности – это модели подразумеваемой волатильности , которые возникают при ценообразовании финансовых опционов . Это параметр (подразумеваемая волатильность), который необходимо изменить, чтобы формула Блэка-Шоулза соответствовала рыночным ценам. В частности, в течение определенного срока действия опционы, цена исполнения которых существенно отличается от цены базового актива, имеют более высокие цены (и, следовательно, подразумеваемую волатильность), чем предполагают стандартные модели ценообразования опционов. Эти опционы называются либо «глубоко в деньгах» , либо «вне денег» .
Построение графика подразумеваемой волатильности относительно цен исполнения для данного срока действия дает искаженную «улыбку» вместо ожидаемой ровной поверхности. Модель различается на разных рынках. Опционы на акции, торгуемые на американских рынках, не демонстрировали улыбку волатильности до краха 1987 года, но начали проявлять ее после. [1] Считается, что переоценка инвесторами вероятности «толстого хвоста» привела к повышению цен на опционы «вне денег». Эта аномалия подразумевает недостатки стандартной модели ценообразования опционов Блэка-Шоулза , которая предполагает постоянную волатильность и логарифмически нормальное распределение доходности базового актива. Однако эмпирические распределения доходности активов имеют тенденцию иметь «жирные хвосты» ( эксцесс ) и асимметрию. Моделирование улыбки волатильности является активной областью исследований в области количественных финансов , и более совершенные модели ценообразования, такие как модель стохастической волатильности, частично решают эту проблему.
Связанной с этим концепцией является концепция временной структуры волатильности , которая описывает, как (подразумеваемая) волатильность различается для связанных опционов с разными сроками погашения. Поверхность подразумеваемой волатильности представляет собой трехмерный график, который отображает улыбку волатильности и временную структуру волатильности на консолидированной трехмерной поверхности для всех опционов на данный базовый актив.
Подразумеваемая волатильность
[ редактировать ]В модели Блэка-Шоулза теоретическая стоимость ванильного опциона представляет собой монотонно возрастающую функцию волатильности базового актива. Это означает, что обычно можно вычислить уникальную подразумеваемую волатильность на основе заданной рыночной цены опциона. Эту подразумеваемую волатильность лучше всего рассматривать как изменение масштаба цен опционов, которое делает сравнение между различными страйками, сроками действия и базовыми активами более простым и интуитивным.
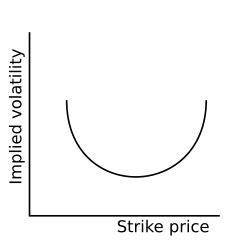
Когда подразумеваемая волатильность отображается в зависимости от цены исполнения , результирующий график обычно имеет нисходящий наклон для фондовых рынков или в форме долины для валютных рынков. Для рынков, где график имеет нисходящий наклон, например, для опционов на акции, термин « перекос волатильности часто используется ». Для других рынков, таких как валютные опционы или опционы на индексы акций, где типичный график располагается на обоих концах, более знакомый термин « улыбка волатильности используется ». Например, подразумеваемая волатильность для опционов на акции с потенциалом роста (т.е. с высоким страйком) обычно ниже, чем для опционов на акции «при деньгах». Однако подразумеваемая волатильность опционов на валютные контракты имеет тенденцию расти как в сторону снижения, так и в сторону повышения. На фондовых рынках возле денег часто можно наблюдать небольшую наклоненную улыбку как излом на общем нисходящем графике скрытой волатильности. Иногда термин «ухмылка» используется для описания кривой улыбки.
Участники рынка используют термин подразумеваемая волатильность для обозначения параметра волатильности для опциона ATM (при деньгах). Корректировки этого значения осуществляются путем включения значений разворота риска и разворота (перекосов) для определения фактической меры волатильности, которая может использоваться для опционов с дельтой, отличной от 50.
Формула
[ редактировать ]где:
- — это подразумеваемая волатильность, при которой x %-delta. на рынке торгуется колл
- — подразумеваемая волатильность опциона x %-дельта-пут
- ATM — это форвардный объем «при деньгах», при котором на рынке торгуются опционы «колл» и «пут» банкомата.
Развороты риска обычно обозначаются как развороты риска дельты x % и, по сути, представляют собой длинный колл-опцион x % дельты и короткий дельта-пут x %.
С другой стороны, Butterfly — это стратегия, состоящая из:− y % delta fly, что означает длинный y % дельта-колл, длинный y % дельта-пут, короткий колл-банкомат и короткий пут-банкомат (форма маленькой шляпы).
Подразумеваемая волатильность и историческая волатильность
[ редактировать ]Полезно отметить, что подразумеваемая волатильность связана с исторической волатильностью , но они различны. Историческая волатильность – это прямая мера движения цены базового актива (реализованная волатильность) за недавнюю историю (например, за 21-дневный период). Подразумеваемая волатильность, напротив, определяется рыночной ценой самого производного контракта, а не базового актива. Таким образом, разные производные контракты на один и тот же базовый актив имеют разную подразумеваемую волатильность в зависимости от собственной динамики спроса и предложения . Например, опцион колл IBM со страйком 100 долларов США и сроком действия 6 месяцев может иметь подразумеваемую волатильность 18%, тогда как опцион пут со страйком 105 долларов США и сроком действия 1 месяц может иметь подразумеваемую волатильность 21%. В то же время историческая волатильность акций IBM за предыдущий 21-дневный период могла составлять 17% (все волатильности выражены в процентных изменениях в годовом исчислении).
Временная структура волатильности
[ редактировать ]Для опционов с разными сроками погашения мы также видим характерные различия в подразумеваемой волатильности. Однако в этом случае доминирующий эффект связан с подразумеваемым влиянием рынка на предстоящие события. Например, хорошо известно, что реализованная волатильность цен на акции значительно возрастает в тот день, когда компания сообщает о своих доходах. Соответственно, мы видим, что подразумеваемая волатильность опционов будет расти в течение периода, предшествующего объявлению о прибылях и убытках, а затем снова падать, как только цена акций воспримет новую информацию. Опционы с более ранним сроком погашения демонстрируют большие колебания подразумеваемой волатильности (иногда называемые «объемом от волатильности»), чем опционы с более длительными сроками погашения.
Другие опционные рынки демонстрируют иное поведение. Например, опционы на товарные фьючерсы обычно демонстрируют повышенную подразумеваемую волатильность непосредственно перед объявлением прогнозов урожая. Опционы на фьючерсы на казначейские векселя США демонстрируют повышенную подразумеваемую волатильность непосредственно перед заседаниями Совета Федеральной резервной системы (когда объявляются изменения в краткосрочных процентных ставках).
Рынок включает в себя множество других типов событий во временную структуру волатильности. Например, влияние предстоящих результатов испытаний лекарства может вызвать подразумеваемые колебания волатильности акций фармацевтических компаний. Ожидаемая дата разрешения патентного спора может повлиять на акции технологических компаний и т. д.
Временные структуры волатильности отражают взаимосвязь между подразумеваемой волатильностью и временем до истечения срока действия. Временные структуры предоставляют трейдерам еще один метод оценки дешевых или дорогих опционов.
Поверхность подразумеваемой волатильности
[ редактировать ]Часто бывает полезно построить график подразумеваемой волатильности как функции цены исполнения и времени до погашения. [2] В результате получается двумерная кривая поверхность, построенная в трех измерениях, на которой текущая рыночная подразумеваемая волатильность ( ось z ) для всех опционов на базовый актив отображается в зависимости от цены ( ось y ) и времени до погашения ( ось x ) "). Это определяет абсолютную поверхность подразумеваемой волатильности ; изменение координат так, что цена заменяется дельтой, дает относительную поверхность подразумеваемой волатильности .
Поверхность подразумеваемой волатильности одновременно показывает и улыбку волатильности, и временную структуру волатильности. Трейдеры опционов используют график подразумеваемой волатильности, чтобы быстро определить форму поверхности подразумеваемой волатильности и выявить любые области, где наклон графика (и, следовательно, относительная подразумеваемая волатильность) выходит за рамки нормы.
На графике показана поверхность подразумеваемой волатильности для всех опционов пут на конкретную цену базовой акции. Ось z представляет подразумеваемую волатильность в процентах, а оси x и y представляют дельту опциона и количество дней до погашения. Обратите внимание, что для поддержания паритета пут-колл дельта-пут 20 должен иметь ту же подразумеваемую волатильность, что и дельта-колл 80. На этой поверхности мы видим, что базовый символ имеет как перекос волатильности (наклон вдоль оси дельты), так и временную структуру волатильности, указывающую на ожидаемое событие в ближайшем будущем.
Эволюция: Липкий
[ редактировать ]Поверхность подразумеваемой волатильности статична : она описывает подразумеваемую волатильность в данный момент времени. То, как меняется поверхность по мере изменения пятна, называется эволюцией поверхности подразумеваемой волатильности .
Общие эвристики включают в себя:
- «липкий страйк» (или «липкий страйк», или «прилипающий страйк»): если спот меняется, подразумеваемая волатильность опциона с заданным абсолютным страйком не меняется.
- «липкая денежность » (также известная как «липкая дельта»; см. « денежность », чтобы узнать, почему это эквивалентные термины): если спот меняется, подразумеваемая волатильность опциона с заданной денежностью (дельтой) не меняется. (Здесь «Дельта» означает «коррекция дельта-волатильности», а не «Дельта» в переводе с греческого языка. Другими словами, относительная поправка волатильности к волатильности страйка банкоматов, которая всегда равна 100% денежности, как можно ближе к текущей цене базового актива, и 0 для корректировки дельта-волатильности.)
Таким образом, если спот-опцион переместится со 100 до 120 долларов, «липкий страйк» будет предсказывать, что подразумеваемая волатильность опциона «страйк» в 120 долларов будет такой же, какой она была до изменения (хотя он и перешел от OTM к ATM), в то время как «липкая дельта» будет предсказывать, что волатильность опциона «страйк» на 120 долларов будет такой же, как и подразумеваемая волатильность опциона «страйк» на 100 долларов до движения (поскольку оба они являются банкоматами в то время).
Моделирование волатильности
[ редактировать ]Методы моделирования улыбки волатильности включают модели стохастической волатильности и модели локальной волатильности . Обсуждение различных альтернативных подходов, разработанных здесь, см. в разделах «Финансовая экономика § Проблемы и критика» и «Модель Блэка – Шоулза § Волатильность» .
См. также
[ редактировать ]- Волатильность (финансы)
- Стохастическая волатильность
- Модель волатильности SABR
- Метод Ванна Волга
- Модель Хестона
- Подразумеваемое биномиальное дерево
- Подразумеваемое трехчленное дерево
- Биномиальное дерево Эджворта
- Финансовая экономика § Отклонения от нормальности
- Риск волатильности
Ссылки
[ редактировать ]- ^ Халл, Джон К. (2003). Опционы, фьючерсы и другие деривативы (5-е изд.). Прентис-Холл. п. 335. ИСБН 0-13-046592-5 .
- ^ Махдави Дамгани, Бабак (2013). «Деарбитраж со слабой улыбкой: применение для снижения риска». Уилмотт . 2013 (1): 40–49. дои : 10.1002/wilm.10201 .
Внешние ссылки
[ редактировать ]- Эмануэль Дерман, Улыбка волатильности и ее подразумеваемое дерево (РИСК, 7–2 февраля 1994 г., стр. 139–145, стр. 32–39) (PDF)
- Марк Рубинштейн, Неявные биномиальные деревья (PDF)
- Дамиано Бриго, Фабио Меркурио, Франческо Раписарда и Джулио Сарторелли, Моделирование улыбки волатильности с помощью смешанных стохастических дифференциальных уравнений (PDF)
- Визуализация улыбки волатильности
- К. Грунспен, «Асимптотические разложения для подразумеваемой логнормальной волатильности: подход без модели»
- Ю. Ли, «Финансовая модель с привязкой к среднему значению и ценообразование опционов»
- примеры улыбок/перекосов волатильности сырьевых товаров






