Текущая статистика

Статистика Каниадакиса (также известная как κ-статистика ) представляет собой обобщение статистической механики Больцмана-Гиббса . основанный на релятивистском обобщение классической энтропии Больцмана-Гиббса-Шеннона (обычно называемой энтропией Каниадакиса или κ-энтропией). Представлен греко-итальянским физиком Джорджио Каниадакисом в 2001 году. κ-статистическая механика сохраняет основные черты обычной статистической механики и в последние годы привлекла интерес многих исследователей. κ-распределение в настоящее время считается одним из наиболее жизнеспособных кандидатов для объяснения сложных физических , естественные или искусственные системы, включающие статистические степенные распределения . Статистика Каниадакиса успешно применяется при описании множества систем в области космологии , астрофизики , конденсированное вещество , квантовая физика , сейсмология , геномика , экономика , эпидемиология , и многие другие.

Математический формализм

Математический формализм κ-статистики порождается κ-деформированными функциями, особенно κ-экспоненциальной функцией.

κ-экспоненциальная функция

График κ-экспоненциальной функции $\exp _{\kappa }(x)$ для трех разных значений κ. Сплошная черная кривая, соответствующая обычной показательной функции. $\exp(x)$ ( $\kappa =0$).

Экспоненциальная (или κ-экспоненциальная) функция Каниадакиса представляет собой однопараметрическое обобщение экспоненциальной функции, определяемое формулой:

$\exp _{\kappa }(x)={\begin{cases}{\Big (}{\sqrt {1+\kappa ^{2}x^{2}}}+\kappa x{\Big )}^{\frac {1}{\kappa }}&{\text{if }}0<\kappa <1.\\[6pt]\exp(x)&{\text{if }}\kappa =0,\\[8pt]\end{cases}}$

с $\exp _{-\kappa }(x)=\exp _{\kappa }(x)$.

κ-экспонента для $0<\kappa <1$ также можно записать в виде:

$\exp _{\kappa }(x)=\exp {\Bigg (}{\frac {1}{\kappa }}{\text{arcsinh}}(\kappa x){\Bigg )}.$

Первые пять членов Тейлора разложения $\exp _{\kappa }(x)$ даны:

$\exp _{\kappa }(x)=1+x+{\frac {x^{2}}{2}}+(1-\kappa ^{2}){\frac {x^{3}}{3!}}+(1-4\kappa ^{2}){\frac {x^{4}}{4!}}+\cdots$

где первые три такие же, как типичная показательная функция .

Основные свойства

κ-экспоненциальная функция обладает следующими свойствами показательной функции:

$\exp _{\kappa }(x)\in \mathbb {C} ^{\infty }(\mathbb {R} )$

${\frac {d}{dx}}\exp _{\kappa }(x)>0$

${\frac {d^{2}}{dx^{2}}}\exp _{\kappa }(x)>0$

$\exp _{\kappa }(-\infty )=0^{+}$

$\exp _{\kappa }(0)=1$

$\exp _{\kappa }(+\infty )=+\infty$

$\exp _{\kappa }(x)\exp _{\kappa }(-x)=-1$

Для реального числа $r$, κ-экспонента обладает свойством:

${\Big [}\exp _{\kappa }(x){\Big ]}^{r}=\exp _{\kappa /r}(rx)$.

κ-логарифмическая функция

График κ-логарифмической функции $\ln _{\kappa }(x)$ для трех разных значений κ. Сплошная черная кривая, соответствующая обычной логарифмической функции. $\ln(x)$ ( $\kappa =0$).

Логарифм Каниадакиса (или κ-логарифм) представляет собой релятивистское однопараметрическое обобщение обычной функции логарифма:

$\ln _{\kappa }(x)={\begin{cases}{\frac {x^{\kappa }-x^{-\kappa }}{2\kappa }}&{\text{if }}0<\kappa <1,\\[8pt]\ln(x)&{\text{if }}\kappa =0,\\[8pt]\end{cases}}$

с $\ln _{-\kappa }(x)=\ln _{\kappa }(x)$, которая является обратной функцией κ-экспоненты:

$\ln _{\kappa }{\Big (}\exp _{\kappa }(x){\Big )}=\exp _{\kappa }{\Big (}\ln _{\kappa }(x){\Big )}=x.$

κ-логарифм для $0<\kappa <1$ также можно записать в виде:

$\ln _{\kappa }(x)={\frac {1}{\kappa }}\sinh {\Big (}\kappa \ln(x){\Big )}$

Первые три члена Тейлора разложения $\ln _{\kappa }(x)$ даны:

$\ln _{\kappa }(1+x)=x-{\frac {x^{2}}{2}}+\left(1+{\frac {\kappa ^{2}}{2}}\right){\frac {x^{3}}{3}}-\cdots$

следуя правилу

$\ln _{\kappa }(1+x)=\sum _{n=1}^{\infty }b_{n}(\kappa )\,(-1)^{n-1}\,{\frac {x^{n}}{n}}$

с $b_{1}(\kappa )=1$, и

$b_{n}(\kappa )(x)={\begin{cases}1&{\text{if }}n=1,\\[8pt]{\frac {1}{2}}{\Big (}1-\kappa {\Big )}{\Big (}1-{\frac {\kappa }{2}}{\Big )}...{\Big (}1-{\frac {\kappa }{n-1}}{\Big )},\,+\,{\frac {1}{2}}{\Big (}1+\kappa {\Big )}{\Big (}1+{\frac {\kappa }{2}}{\Big )}...{\Big (}1+{\frac {\kappa }{n-1}}{\Big )}&{\text{for }}n>1,\\[8pt]\end{cases}}$

где $b_{n}(0)=1$ и $b_{n}(-\kappa )=b_{n}(\kappa )$. Два первых члена Тейлора разложения $\ln _{\kappa }(x)$ аналогичны обычной логарифмической функции .

Основные свойства

κ-логарифмическая функция обладает следующими свойствами логарифмической функции:

$\ln _{\kappa }(x)\in \mathbb {C} ^{\infty }(\mathbb {R} ^{+})$

${\frac {d}{dx}}\ln _{\kappa }(x)>0$

${\frac {d^{2}}{dx^{2}}}\ln _{\kappa }(x)<0$

$\ln _{\kappa }(0^{+})=-\infty$

$\ln _{\kappa }(1)=0$

$\ln _{\kappa }(+\infty )=+\infty$

$\ln _{\kappa }(1/x)=-\ln _{\kappa }(x)$

Для реального числа $r$, κ-логарифм обладает свойством:

$\ln _{\kappa }(x^{r})=r\ln _{r\kappa }(x)$

κ-Алгебра

я κ

Для любого $x,y\in \mathbb {R}$ и $|\kappa |<1$, сумма Каниадакиса (или κ-сумма) определяется следующим законом композиции:

$x{\stackrel {\kappa }{\oplus }}y=x{\sqrt {1+\kappa ^{2}y^{2}}}+y{\sqrt {1+\kappa ^{2}x^{2}}}$,

это также можно записать в форме:

$x{\stackrel {\kappa }{\oplus }}y={1 \over \kappa }\,\sinh \left({\rm {arcsinh}}\,(\kappa x)\,+\,{\rm {arcsinh}}\,(\kappa y)\,\right)$,

где обычная сумма является частным случаем классического предела $\kappa \rightarrow 0$: $x{\stackrel {0}{\oplus }}y=x+y$.

κ-сумма, как и обычная сумма, обладает следующими свойствами:

${\text{1. associativity:}}\quad (x{\stackrel {\kappa }{\oplus }}y){\stackrel {\kappa }{\oplus }}z=x{\stackrel {\kappa }{\oplus }}(y{\stackrel {\kappa }{\oplus }}z)$

${\text{2. neutral element:}}\quad x{\stackrel {\kappa }{\oplus }}0=0{\stackrel {\kappa }{\oplus }}x=x$

${\text{3. opposite element:}}\quad x{\stackrel {\kappa }{\oplus }}(-x)=(-x){\stackrel {\kappa }{\oplus }}x=0$

${\text{4. commutativity:}}\quad x{\stackrel {\kappa }{\oplus }}y=y{\stackrel {\kappa }{\oplus }}x$

κ-разница ${\stackrel {\kappa }{\ominus }}$ дается $x{\stackrel {\kappa }{\ominus }}y=x{\stackrel {\kappa }{\oplus }}(-y)$.

Фундаментальное свойство $\exp _{\kappa }(-x)\exp _{\kappa }(x)=1$ возникает как частный случай более общего выражения, приведенного ниже: $\exp _{\kappa }(x)\exp _{\kappa }(y)=exp_{\kappa }(x{\stackrel {\kappa }{\oplus }}y)$

Кроме того, κ-функции и κ-сумма представляют собой следующие соотношения:

$\ln _{\kappa }(x\,y)=\ln _{\kappa }(x){\stackrel {\kappa }{\oplus }}\ln _{\kappa }(y)$

κ-продукт

Для любого $x,y\in \mathbb {R}$ и $|\kappa |<1$, произведение Каниадакиса (или κ-произведение) определяется следующим законом композиции:

$x{\stackrel {\kappa }{\otimes }}y={1 \over \kappa }\,\sinh \left(\,{1 \over \kappa }\,\,{\rm {arcsinh}}\,(\kappa x)\,\,{\rm {arcsinh}}\,(\kappa y)\,\right)$,

где обычное произведение является частным случаем классического предела $\kappa \rightarrow 0$: $x{\stackrel {0}{\otimes }}y=x\times y=xy$.

κ-произведение, как и обычное произведение, обладает следующими свойствами:

${\text{1. associativity:}}\quad (x{\stackrel {\kappa }{\otimes }}y){\stackrel {\kappa }{\otimes }}z=x{\stackrel {\kappa }{\otimes }}(y{\stackrel {\kappa }{\otimes }}z)$

${\text{2. neutral element:}}\quad x{\stackrel {\kappa }{\otimes }}I=I{\stackrel {\kappa }{\otimes }}x=x\quad {\text{for}}\quad I=\kappa ^{-1}\sinh \kappa {\stackrel {\kappa }{\oplus }}x=x$

${\text{3. inverse element:}}\quad x{\stackrel {\kappa }{\otimes }}{\overline {x}}={\overline {x}}{\stackrel {\kappa }{\otimes }}x=I\quad {\text{for}}\quad {\overline {x}}=\kappa ^{-1}\sinh(\kappa ^{2}/{\rm {arcsinh}}\,(\kappa x))$

${\text{4. commutativity:}}\quad x{\stackrel {\kappa }{\otimes }}y=y{\stackrel {\kappa }{\otimes }}x$

κ-деление ${\stackrel {\kappa }{\oslash }}$ дается $x{\stackrel {\kappa }{\oslash }}y=x{\stackrel {\kappa }{\otimes }}{\overline {y}}$.

κ-сумма ${\stackrel {\kappa }{\oplus }}$ и κ-произведение ${\stackrel {\kappa }{\otimes }}$ подчиняются распределительному закону: $z{\stackrel {\kappa }{\otimes }}(x{\stackrel {\kappa }{\oplus }}y)=(z{\stackrel {\kappa }{\otimes }}x){\stackrel {\kappa }{\oplus }}(z{\stackrel {\kappa }{\otimes }}y)$.

Фундаментальное свойство $\ln _{\kappa }(1/x)=-\ln _{\kappa }(x)$ возникает как частный случай более общего выражения, приведенного ниже:

$\ln _{\kappa }(x\,y)=\ln _{\kappa }(x){\stackrel {\kappa }{\oplus }}\ln _{\kappa }(y)$

Кроме того, κ-функции и κ-произведение представляют следующие отношения:

$\exp _{\kappa }(x){\stackrel {\kappa }{\otimes }}\exp _{\kappa }(y)=\exp _{\kappa }(x\,+\,y)$

$\ln _{\kappa }(x\,{\stackrel {\kappa }{\otimes }}\,y)=\ln _{\kappa }(x)+\ln _{\kappa }(y)$

κ-исчисление

κ-Дифференциал

Дифференциал Каниадакиса (или κ-дифференциал) $x$ определяется:

$\mathrm {d} _{\kappa }x={\frac {\mathrm {d} \,x}{\displaystyle {\sqrt {1+\kappa ^{2}\,x^{2}}}}}$.

Итак, κ-производная функции $f(x)$ связана с производной Лейбница через:

${\frac {\mathrm {d} f(x)}{\mathrm {d} _{\kappa }x}}=\gamma _{\kappa }(x){\frac {\mathrm {d} f(x)}{\mathrm {d} x}}$,

где $\gamma _{\kappa }(x)={\sqrt {1+\kappa ^{2}x^{2}}}$ является фактором Лоренца. Обыкновенная производная ${\frac {\mathrm {d} f(x)}{\mathrm {d} x}}$ является частным случаем κ-производной ${\frac {\mathrm {d} f(x)}{\mathrm {d} _{\kappa }x}}$ в классическом пределе $\kappa \rightarrow 0$.

κ-Интеграл

Интеграл Каниадакиса (или κ-интеграл) — это обратный оператор κ-производной, определяемой через

$\int \mathrm {d} _{\kappa }x\,\,f(x)=\int {\frac {\mathrm {d} \,x}{\sqrt {1+\kappa ^{2}\,x^{2}}}}\,\,f(x)$,

который восстанавливает обычный интеграл в классическом пределе $\kappa \rightarrow 0$.

κ-Тригонометрия

κ-Циклическая тригонометрия

[нажмите на рисунок] График функций κ-синус и κ-косинус для $\kappa =0$ (черная кривая) и $\kappa =0.1$ (синяя кривая).

Циклическая тригонометрия Каниадакиса (или κ-циклическая тригонометрия) основана на функциях κ-циклического синуса (или κ-синуса) и κ-циклического косинуса (или κ-косинуса), определяемых следующим образом:

$\sin _{\kappa }(x)={\frac {\exp _{\kappa }(ix)-\exp _{\kappa }(-ix)}{2i}}$,

$\cos _{\kappa }(x)={\frac {\exp _{\kappa }(ix)+\exp _{\kappa }(-ix)}{2}}$,

где κ-обобщенная формула Эйлера имеет вид

$\exp _{\kappa }(\pm ix)=\cos _{\kappa }(x)\pm i\sin _{\kappa }(x)$.:

κ-циклическая тригонометрия сохраняет фундаментальные выражения обычной циклической тригонометрии, которая является частным случаем в пределе κ → 0, такие как:

$\cos _{\kappa }^{2}(x)+\sin _{\kappa }^{2}(x)=1$

$\sin _{\kappa }(x{\stackrel {\kappa }{\oplus }}y)=\sin _{\kappa }(x)\cos _{\kappa }(y)+\cos _{\kappa }(x)\sin _{\kappa }(y)$.

κ-циклический касательный и κ-циклический котангенс задаются формулами:

$\tan _{\kappa }(x)={\frac {\sin _{\kappa }(x)}{\cos _{\kappa }(x)}}$

$\cot _{\kappa }(x)={\frac {\cos _{\kappa }(x)}{\sin _{\kappa }(x)}}$.

κ-циклические тригонометрические функции становятся обычной тригонометрической функцией в классическом пределе $\kappa \rightarrow 0$.

κ-обратная циклическая функция

Обратные циклические функции Каниадакиса (или κ-обратные циклические функции) связаны с κ-логарифмом:

${\rm {arcsin}}_{\kappa }(x)=-i\ln _{\kappa }\left({\sqrt {1-x^{2}}}+ix\right)$,

${\rm {arccos}}_{\kappa }(x)=-i\ln _{\kappa }\left({\sqrt {x^{2}-1}}+x\right)$,

${\rm {arctan}}_{\kappa }(x)=i\ln _{\kappa }\left({\sqrt {\frac {1-ix}{1+ix}}}\right)$,

${\rm {arccot}}_{\kappa }(x)=i\ln _{\kappa }\left({\sqrt {\frac {ix+1}{ix-1}}}\right)$.

κ-Гиперболическая тригонометрия

Гиперболическая тригонометрия Каниадакиса (или κ-гиперболическая тригонометрия) основана на κ-гиперболическом синусе и κ-гиперболическом косинусе, определяемых формулой:

$\sinh _{\kappa }(x)={\frac {\exp _{\kappa }(x)-\exp _{\kappa }(-x)}{2}}$,

$\cosh _{\kappa }(x)={\frac {\exp _{\kappa }(x)+\exp _{\kappa }(-x)}{2}}$,

где формула κ-Эйлера

$\exp _{\kappa }(\pm x)=\cosh _{\kappa }(x)\pm \sinh _{\kappa }(x)$.

κ-гиперболический тангенс и κ-гиперболический котангенс определяются формулами:

$\tanh _{\kappa }(x)={\frac {\sinh _{\kappa }(x)}{\cosh _{\kappa }(x)}}$

$\coth _{\kappa }(x)={\frac {\cosh _{\kappa }(x)}{\sinh _{\kappa }(x)}}$.

κ-гиперболические тригонометрические функции становятся обычными гиперболическими тригонометрическими функциями в классическом пределе $\kappa \rightarrow 0$.

Из формулы κ-Эйлера и свойства $\exp _{\kappa }(-x)\exp _{\kappa }(x)=1$ основное выражение κ-гиперболической тригонометрии задается следующим образом:

$\cosh _{\kappa }^{2}(x)-\sinh _{\kappa }^{2}(x)=1$

κ-обратная гиперболическая функция

Обратные гиперболические функции Каниадакиса (или κ-обратные гиперболические функции) связаны с κ-логарифмом:

${\rm {arcsinh}}_{\kappa }(x)=\ln _{\kappa }\left({\sqrt {1+x^{2}}}+x\right)$,

${\rm {arccosh}}_{\kappa }(x)=\ln _{\kappa }\left({\sqrt {x^{2}-1}}+x\right)$,

${\rm {arctanh}}_{\kappa }(x)=\ln _{\kappa }\left({\sqrt {\frac {1+x}{1-x}}}\right)$,

${\rm {arccoth}}_{\kappa }(x)=\ln _{\kappa }\left({\sqrt {\frac {1-x}{1+x}}}\right)$,

в котором справедливы следующие соотношения:

${\rm {arcsinh}}_{\kappa }(x)={\rm {sign}}(x){\rm {arccosh}}_{\kappa }\left({\sqrt {1+x^{2}}}\right)$,

${\rm {arcsinh}}_{\kappa }(x)={\rm {arctanh}}_{\kappa }\left({\frac {x}{\sqrt {1+x^{2}}}}\right)$,

${\rm {arcsinh}}_{\kappa }(x)={\rm {arccoth}}_{\kappa }\left({\frac {\sqrt {1+x^{2}}}{x}}\right)$.

κ-циклическая и κ-гиперболическая тригонометрические функции связаны следующими соотношениями:

${\rm {sin}}_{\kappa }(x)=-i{\rm {sinh}}_{\kappa }(ix)$,

${\rm {cos}}_{\kappa }(x)={\rm {cosh}}_{\kappa }(ix)$,

${\rm {tan}}_{\kappa }(x)=-i{\rm {tanh}}_{\kappa }(ix)$,

${\rm {cot}}_{\kappa }(x)=i{\rm {coth}}_{\kappa }(ix)$,

${\rm {arcsin}}_{\kappa }(x)=-i\,{\rm {arcsinh}}_{\kappa }(ix)$,

${\rm {arccos}}_{\kappa }(x)\neq -i\,{\rm {arccosh}}_{\kappa }(ix)$,

${\rm {arctan}}_{\kappa }(x)=-i\,{\rm {arctanh}}_{\kappa }(ix)$,

${\rm {arccot}}_{\kappa }(x)=i\,{\rm {arccoth}}_{\kappa }(ix)$.

Относительная энтропия

Статистика Каниадакиса основана на κ-энтропии Каниадакиса, которая определяется через:

$S_{\kappa }{\big (}p{\big )}=-\sum _{i}p_{i}\ln _{\kappa }{\big (}p_{i}{\big )}=\sum _{i}p_{i}\ln _{\kappa }{\bigg (}{\frac {1}{p_{i}}}{\bigg )}$

где $p=\{p_{i}=p(x_{i});x\in \mathbb {R} ;i=1,2,...,N;\sum _{i}p_{i}=1\}$ это функция распределения вероятностей, определенная для случайной величины $X$, и $0\leq |\kappa |<1$ является энтропийным индексом.

κ-энтропия Каниадакиса термодинамически стабильна и устойчива по Леше. и подчиняется аксиомам Шеннона-Хинчина непрерывности, максимальности, обобщенной аддитивности и расширяемости.

Распределения Каниадакиса

Основная статья: Распространение Каниадакиса

Распределение Каниадакиса (или κ -распределение ) — это распределение вероятностей, полученное в результате максимизации энтропии Каниадакиса при соответствующих ограничениях. В связи с этим появляется несколько вероятностных распределений для анализа широкого спектра феноменологии, связанной с экспериментальными степенными статистическими распределениями.

κ-Экспоненциальное распределение

Основная статья: Каниадакис Экспоненциальное распределение

κ-гауссово распределение

Основная статья: Гауссово распределение Каниадакиса

κ-гамма-распределение

Основная статья: Гамма-распределение Каниадакиса

κ-распределение Вейбулла

Основная статья: Распределение Каниадакиса Вейбулла

κ-Логистическое распределение

Основная статья: Каниадакис Логистическое распределение

Интегральное преобразование Кианадакиса

κ-преобразование Лапласа

Преобразование Каниадакиса Лапласа (или κ-преобразование Лапласа) представляет собой κ-деформированное интегральное преобразование обычного преобразования Лапласа . Преобразование κ-Лапласа преобразует функцию $f$ действительной переменной $t$ к новой функции $F_{\kappa }(s)$ в комплексной частотной области, представленной комплексной переменной $s$. Это κ-интегральное преобразование определяется как:

$F_{\kappa }(s)={\cal {L}}_{\kappa }\{f(t)\}(s)=\int _{\,0}^{\infty }\!f(t)\,[\exp _{\kappa }(-t)]^{s}\,dt$

Обратное κ-преобразование Лапласа определяется формулой:

$f(t)={\cal {L}}_{\kappa }^{-1}\{F_{\kappa }(s)\}(t)={{\frac {1}{2\pi i}}\int _{c-i\infty }^{c+i\infty }\!F_{\kappa }(s)\,{\frac {[\exp _{\kappa }(t)]^{s}}{\sqrt {1+\kappa ^{2}t^{2}}}}\,ds}$

Обычное преобразование Лапласа и его обратное преобразование восстанавливаются как $\kappa \rightarrow 0$.

Характеристики

Пусть две функции $f(t)={\cal {L}}_{\kappa }^{-1}\{F_{\kappa }(s)\}(t)$ и $g(t)={\cal {L}}_{\kappa }^{-1}\{G_{\kappa }(s)\}(t)$и соответствующие им κ-преобразования Лапласа $F_{\kappa }(s)$ и $G_{\kappa }(s)$В следующей таблице представлены основные свойства преобразования κ-Лапласа:

Свойства преобразования κ-Лапласа

Свойство	$f(t)$	$F_{\kappa }(s)$
Линейность	$a\,f(t)+b\,g(t)$	$a\,F_{\kappa }(s)+b\,G_{\kappa }(s)$
Масштабирование времени	$f(at)$	${\frac {1}{a}}\,F_{\kappa /a}({\frac {s}{a}})$
Сдвиг частоты	$f(t)\,[\exp _{\kappa }(-t)]^{a}$	$F_{\kappa }(s-a)$
Производная	${\frac {d\,f(t)}{dt}}$	$s\,{\cal {L}}_{\kappa }\left\{{\frac {f(t)}{\sqrt {1+\kappa ^{2}t^{2}}}}\right\}(s)-f(0)$
Производная	${\frac {d}{dt}}\,{\sqrt {1+\kappa ^{2}t^{2}}}\,f(t)$	$s\,F_{\kappa }(s)-f(0)$
во временной области Интеграция	${\frac {1}{\sqrt {1+\kappa ^{2}t^{2}}}}\,\int _{0}^{t}f(w)dw$	${\frac {1}{s}}\,F_{\kappa }(s)$
	$f(t)\,[\ln(\exp _{\kappa }(t))]^{n}$	$(-1)^{n}{\frac {d^{n}F_{\kappa }(s)}{ds^{n}}}$
	$f(t)\,[\ln(\exp _{\kappa }(t))]^{-n}$	$\int _{s}^{+\infty }dw_{n}\int _{w_{n}}^{+\infty }dw_{n-1}...\int _{w_{3}}^{+\infty }dw_{2}\int _{w_{2}}^{+\infty }dw_{1}\,F_{\kappa }(w_{1})$
Дельта-функция Дирака	$\delta (t-\tau )$	$[\exp _{\kappa }(-\tau )]^{s}$
Функция единицы Хевисайда	$u(t-\tau )$	${\frac {s{\sqrt {1+\kappa ^{2}\tau ^{2}}}+\kappa ^{2}\tau }{s^{2}-\kappa ^{2}}}\,[\exp _{\kappa }(-\tau )]^{s}$
Функция мощности	$t^{\nu -1}$	${\frac {s^{2}}{s^{2}-\kappa ^{2}\nu ^{2}}}\,{\frac {\Gamma _{\frac {\kappa }{s}}(\nu +1)}{\nu \,s^{\nu }}}={\frac {s}{s+|\kappa |\nu }}\,{\frac {\Gamma (\nu )}{|2\kappa |^{\nu }}}\,{\frac {\Gamma \left({\frac {s}{|2\kappa |}}-{\frac {\nu }{2}}\right)}{\Gamma \left({\frac {s}{|2\kappa |}}+{\frac {\nu }{2}}\right)}}$
Функция мощности	$t^{2m-1},\ \ m\in Z^{+}$	${\frac {(2m-1)!}{\prod _{j=1}^{m}\left[s^{2}-(2j)^{2}\kappa ^{2}\right]}}$
Функция мощности	$t^{2m},\ \ m\in Z^{+}$	${\frac {(2m)!\,s}{\prod _{j=1}^{m+1}\left[s^{2}-(2j-1)^{2}\kappa ^{2}\right]}}$

Преобразования κ-Лапласа, представленные в последней таблице, сводятся к соответствующим обычным преобразованиям Лапласа в классическом пределе $\kappa \rightarrow 0$.

κ-преобразование Фурье

Преобразование Фурье Каниадакиса (или κ-преобразование Фурье) представляет собой κ-деформированное интегральное преобразование обычного преобразования Фурье , которое согласуется с κ-алгеброй и κ-исчислением. κ-преобразование Фурье определяется как:

${\cal {F}}_{\kappa }[f(x)](\omega )={1 \over {\sqrt {2\,\pi }}}\int \limits _{-\infty }\limits ^{+\infty }f(x)\,\exp _{\kappa }(-x\otimes _{\kappa }\omega )^{i}\,d_{\kappa }x$

который можно переписать как

${\cal {F}}_{\kappa }[f(x)](\omega )={1 \over {\sqrt {2\,\pi }}}\int \limits _{-\infty }\limits ^{+\infty }f(x)\,{\exp(-i\,x_{\{\kappa \}}\,\omega _{\{\kappa \}}) \over {\sqrt {1+\kappa ^{2}\,x^{2}}}}\,dx$

где $x_{\{\kappa \}}={\frac {1}{\kappa }}\,{\rm {arcsinh}}\,(\kappa \,x)$ и $\omega _{\{\kappa \}}={\frac {1}{\kappa }}\,{\rm {arcsinh}}\,(\kappa \,\omega )$. κ-преобразование Фурье обеспечивает асимптотически логарифмически периодическое поведение, деформируя параметры $x$ и $\omega$ в дополнение к коэффициенту демпфирования, а именно ${\sqrt {1+\kappa ^{2}\,x^{2}}}$.

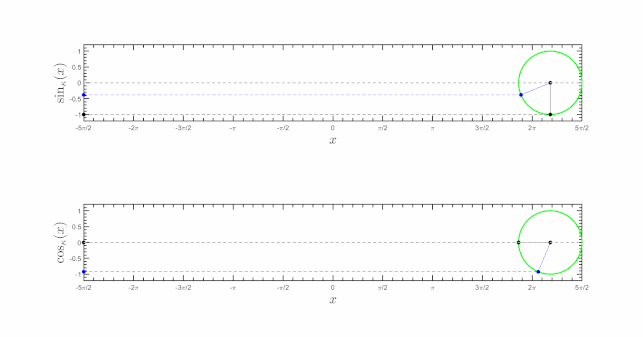
Реальная (верхняя панель) и мнимая (нижняя панель) части ядра. $h_{\kappa }(x,\omega )$ для типичного $\kappa$-ценности и $\omega =1$.

Ядро κ-преобразования Фурье задается формулой:

$h_{\kappa }(x,\omega )={\frac {\exp(-i\,x_{\{\kappa \}}\,\omega _{\{\kappa \}})}{\sqrt {1+\kappa ^{2}\,x^{2}}}}$

Обратное κ-преобразование Фурье определяется как:

${\cal {F}}_{\kappa }[{\hat {f}}(\omega )](x)={1 \over {\sqrt {2\,\pi }}}\int \limits _{-\infty }\limits ^{+\infty }{\hat {f}}(\omega )\,\exp _{\kappa }(\omega \otimes _{\kappa }x)^{i}\,d_{\kappa }\omega$

Позволять $u_{\kappa }(x)={\frac {1}{\kappa }}\cosh {\Big (}\kappa \ln(x){\Big )}$, в следующей таблице показаны κ-преобразования Фурье нескольких известных функций:

κ-преобразование Фурье нескольких функций

	$f(x)$	${\cal {F}}_{\kappa }[f(x)](\omega )$
Ступенчатая функция	$\theta (x)$	${\sqrt {2\,\pi }}\,\delta (\omega )+{1 \over {\sqrt {2\,\pi }}\,i\,\omega _{\{\kappa \}}}$
Модуляция	$\cos _{\kappa }(a{\stackrel {\kappa }{\oplus }}x)$	${\sqrt {\pi \over 2}}\,u_{\kappa }(\exp _{\kappa }(a))\,\left(\delta (\omega +a)+\delta (\omega -a)\right)$
Причинно-следственный $\kappa$-экспоненциальный	$\theta (x)\,\exp _{\kappa }(-a{\stackrel {\kappa }{\otimes }}x)$	${1 \over {\sqrt {2\,\pi }}}{1 \over a_{\{\kappa \}}+i\,\omega _{\{\kappa \}}}$
Симметричный $\kappa$-экспоненциальный	$\exp _{\kappa }(-a{\stackrel {\kappa }{\otimes }}|x|)$	${\sqrt {2 \over \pi }}\,{a_{\{\kappa \}} \over a_{\{\kappa \}}^{2}+\omega _{\{\kappa \}}^{2}}$
Постоянный	$1$	${\sqrt {2\,\pi }}\,\delta (\omega )$
$\kappa$-Фазор	$\exp _{\kappa }\,(a{\stackrel {\kappa }{\otimes }}x)^{i}$	${\sqrt {2\,\pi }}\,u_{\kappa }(\exp _{\kappa }(a))\,\delta (\omega -a)$
Импульс	$\delta (x-a)$	${1 \over {\sqrt {2\,\pi }}}{\exp _{\kappa }\,(\omega {\stackrel {\kappa }{\otimes }}a)^{i} \over u_{\kappa }\left(\exp _{\kappa }\,(a)\right)}$
Знак	Знак $(x)$	${\sqrt {2 \over \pi }}\,\,{1 \over i\,\omega _{\{\kappa \}}}$
Прямоугольный	$\Pi \left({x \over a}\right)$	${\sqrt {2 \over \pi }}\,\,a_{\{\kappa \}}\,{\rm {sinc}}_{\kappa }(\omega {\stackrel {\kappa }{\otimes }}a)$

κ-деформированная версия преобразования Фурье сохраняет основные свойства обычного преобразования Фурье, как показано в следующей таблице.

κ-свойства Фурье

$f(x)$	${\cal {F}}_{\kappa }[f(x)](\omega )$
Линейность	${\cal {F}}_{\kappa }[\alpha \,f(x)+\beta \,g(x)](\omega )=\alpha \,{\cal {F}}_{\kappa }[f(x)](\omega )+\beta \,{\cal {F}}_{\kappa }[g(x)](\omega )$
Масштабирование	${\cal {F}}_{\kappa }\left[f(\alpha \,x)\right](\omega )={1 \over \alpha }\,{\cal {F}}_{\kappa ^{\prime }}\left[f(x)\right](\omega ^{\prime })$ где $\kappa ^{\prime }=\kappa /\alpha$ и $\omega ^{\prime }=(a/\kappa )\,\sinh \left({\rm {arcsinh}}(\kappa \,\omega )/a^{2}\right)$
$\kappa$-Масштабирование	${\cal {F}}_{\kappa }\left[f(\alpha {\stackrel {\kappa }{\otimes }}x)\right](\omega )={1 \over \alpha _{\{\kappa \}}}\,{\cal {F}}_{\kappa }[f(x)]\left({\frac {1}{\alpha }}{\stackrel {\kappa }{\otimes }}\omega \right)$
Комплексное сопряжение	${\cal {F}}_{\kappa }{\big [}f(x){\big ]}^{\ast }(\omega )={\cal {F}}_{\kappa }{\big [}f(x){\big ]}(-\omega )$
Двойственность	${\cal {F}}_{\kappa }{\Big [}{\cal {F}}_{\kappa }{\big [}f(x){\big ]}(\nu ){\Big ]}(\omega )=f(-\omega )$
Обеспечить регресс	${\cal {F}}_{\kappa }\left[f(-x)\right](\omega )={\cal {F}}_{\kappa }[f(x)](-\omega )$
$\kappa$-Сдвиг частоты	${\cal {F}}_{\kappa }\left[\exp _{\kappa }(\omega _{0}{\stackrel {\kappa }{\otimes }}x)^{i}f(x)\right](\omega )={\cal {F}}_{\kappa }[f(x)](\omega {\stackrel {\kappa }{\ominus }}\omega _{0})$
$\kappa$-Сдвиг времени	${\cal {F}}_{\kappa }\left[f(x\,{\stackrel {\kappa }{\oplus }}\,x_{0})\right](\omega )=\exp _{\kappa }(\omega \,{\stackrel {\kappa }{\otimes }}\,x_{0})^{i}\,{\cal {F}}_{\kappa }[f(x)](\omega )$
Преобразование $\kappa$-производная	${\cal {F}}_{\kappa }\left[{\frac {d\,f(x)}{d_{\kappa }x}}\right](\omega )=i\,\omega _{\{\kappa \}}\,{\cal {F}}_{\kappa }[f(x)](\omega )$
$\kappa$-Производная преобразования	${\frac {d}{d_{\kappa }\omega }}\,{\cal {F}}_{\kappa }[f(x)](\omega )=-i\,\omega _{\{\kappa \}}\,{\cal {F}}_{\kappa }\left[x_{\{\kappa \}}\,f(x)\right](\omega )$
Преобразование интеграла	${\cal {F}}_{\kappa }\left[\int \limits _{-\infty }\limits ^{x}f(y)\,dy\right](\omega )={1 \over i\,\omega _{\{\kappa \}}}{\cal {F}}_{\kappa }[f(x)](\omega )+2\,\pi \,{\cal {F}}_{\kappa }[f(x)](0)\,\delta (\omega )$
$\kappa$-Свертка	${\cal {F}}_{\kappa }\left[(f\,{\stackrel {\kappa }{\circledast }}\,g)(x)\right](\omega )={\sqrt {2\,\pi }}\,{\cal {F}}_{\kappa }[f(x)](\omega )\,{\cal {F}}_{\kappa }[g(x)](\omega )$ где $(f\,{\stackrel {\kappa }{\circledast }}\,g)(x)=\int \limits _{-\infty }\limits ^{+\infty }f(y)\,g(x\,{\stackrel {\kappa }{\ominus }}\,y)\,d_{\kappa }y$
Модуляция	${\cal {F}}_{\kappa }\left[f(x)\,g(x)\right](\omega )={1 \over {\sqrt {2\,\pi }}}\left({\cal {F}}_{\kappa }\left[f(x)\right]\,{\stackrel {\kappa }{\circledast }}\,{\cal {F}}_{\kappa }\left[g(x)\right]\right)(\omega )$

Свойства κ-преобразования Фурье, представленные в последней таблице, сводятся к соответствующим обычным преобразованиям Фурье в классическом пределе $\kappa \rightarrow 0$.

См. также

• Джорджио Каниадакис
• Распространение Каниадакиса
• κ-Экспоненциальное распределение Каниадакиса
• κ-гауссово распределение Каниадакиса
• κ-гамма-распределение Каниадакиса
• Распределение Каниадакиса κ-Вейбулла
• Каниадакис κ-Логистическое распределение
• Распределение Кианадакиса κ-Эрланга

Ссылки

• В эту статью включен текст , доступный по лицензии CC BY 3.0 .

Внешние ссылки

• Страница Джорджио Каниадакиса в Google Scholar
• Статистика Каниадакиса на arXiv.org