Постоянная времени

В физике и технике , постоянная времени обычно обозначаемая греческой буквой τ (тау), является параметром, характеризующим реакцию на входной сигнал линейной нестационарной (LTI) системы первого порядка. Постоянная времени является основной характеристической единицей системы LTI первого порядка. Это дает скорость реакции.

Во временной области обычный выбор для изучения временной характеристики — это переходная характеристика на входной сигнал шага или импульсная характеристика на входной сигнал дельта-функции Дирака . В частотной области (например, рассматривая преобразование Фурье переходного процесса или используя входные данные, представляющие собой простую синусоидальную функцию времени) постоянная времени также определяет полосу пропускания нестационарной системы первого порядка, то есть , частота, на которой мощность выходного сигнала падает до половины значения, которое она имеет на низких частотах.

Постоянная времени также используется для характеристики частотной характеристики различных систем обработки сигналов — магнитных лент , радиопередатчиков и приемников , оборудования для резки и воспроизведения записей, а также цифровых фильтров — которые могут быть смоделированы или аппроксимированы системами LTI первого порядка. Другие примеры включают постоянную времени, используемую в системах управления для контроллеров интегрального и дифференциального действия, которые часто являются пневматическими , а не электрическими.

Постоянные времени являются особенностью анализа сосредоточенных систем (метода анализа сосредоточенной мощности) для тепловых систем, используемого, когда объекты охлаждаются или нагреваются равномерно под влиянием конвективного охлаждения или потепления.

Физически постоянная времени представляет собой время, необходимое для того, чтобы реакция системы затухала до нуля, если бы система продолжала распадаться с начальной скоростью, из-за постепенного изменения скорости затухания значение реакции фактически уменьшится до 1. / e ≈ 36,8% за это время (скажем, со ступенчатого уменьшения). системы В возрастающей системе постоянная времени — это время, в течение которого переходная реакция достигает 1 - 1 / e ≈ 63,2% от ее конечного (асимптотического) значения (скажем, при ступенчатом увеличении). При радиоактивном распаде постоянная времени связана с постоянной распада ( λ ) и представляет собой как среднее время жизни распадающейся системы (например, атома) до ее распада, так и время, которое требуется для всех атомов, кроме 36,8%. распадаться. По этой причине постоянная времени больше, чем период полураспада , за который распадается только 50% атомов.

Дифференциальное уравнение

Основная статья: Линейная нестационарная система

Системы LTI первого порядка характеризуются дифференциальным уравнением $$\tau {\frac {dV}{dt}}+V=f(t)$$

где τ представляет собой константу экспоненциального затухания , а V является функцией времени t $$V=V(t).$$Правая часть — это вынуждающая функция f ( t ), описывающая внешнюю движущую функцию времени, которую можно рассматривать как вход системы , на которую V ( t ) является ответом , или выход системы. Классическими примерами f ( t ) являются:

Ступенчатая функция Хевисайда , часто обозначаемая u ( t ) : $$u(t)={\begin{cases}0,&t<0\\1,&t\geq 0\end{cases}}$$импульсная функция , часто обозначаемая δ ( t ) , а также синусоидальная входная функция: $$f(t)=A\sin(2\pi ft)$$или $$f(t)=Ae^{j\omega t},$$где A — амплитуда вынуждающей функции, f — частота в герцах, а ω = 2 π f — частота в радианах в секунду.

Пример решения

Пример решения дифференциального уравнения с начальным значением V ₀ и без вынуждающей функции: $$V(t)=V_{0}e^{-t/\tau }$$

где $$V_{0}=V(t=0)$$

начальное значение V. — Таким образом, ответ представляет собой экспоненциальное затухание с постоянной времени τ .

Обсуждение

Предполагать $$V(t)=V_{0}e^{-t/\tau }.$$

Такое поведение называется «затухающей» экспоненциальной функцией. Время τ (тау) называется «постоянной времени» и может использоваться (как в этом случае) для указания того, насколько быстро затухает экспоненциальная функция.

Здесь:

• t - время (обычно t > 0 в технике управления)
• V ₀ — начальное значение (см. «особые случаи» ниже).

Конкретные случаи

1. Позволять $t=0$; затем $V=V_{0}e^{0}$, и так $V=V_{0}$
2. Позволять $t=\tau$; затем $V=V_{0}e^{-1}\approx 0.37V_{0}$
3. Позволять $V=f(t)=V_{0}e^{-t/\tau }$, и так ${\textstyle \lim _{t\to \infty }f(t)=0}$
4. Позволять $t=5\tau$; затем $V=V_{0}e^{-5}\approx 0.0067V_{0}$

По прошествии периода одной постоянной времени функция достигает e ⁻¹ = примерно 37% от первоначального значения. В случае 4 после пяти постоянных времени функция достигает значения менее 1% от исходного. В большинстве случаев этот порог в 1% считается достаточным, чтобы предположить, что функция затухала до нуля - как правило, в технике управления устойчивой системой является та, которая демонстрирует такое общее затухающее поведение.

Связь постоянной времени с полосой пропускания

Пример реакции системы на функцию синусоидального воздействия. Ось времени в единицах постоянной времени τ . Отклик затухает и превращается в простую синусоидальную волну.

Частотная характеристика системы в зависимости от частоты в единицах полосы пропускания f _{3 дБ} . Отклик нормализуется до значения нулевой частоты, равного единице, и падает до 1/√2 в полосе пропускания.

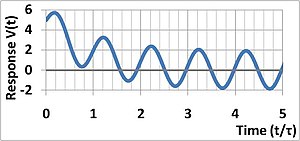
Предположим, что вынуждающая функция выбрана синусоидальной, поэтому:

$$\tau {\frac {dV}{dt}}+V=f(t)=Ae^{j\omega t}.$$

(Отклик на входной сигнал действительного косинуса или синусоидальной волны можно получить, взяв действительную или мнимую часть конечного результата на основании формулы Эйлера .) Общее решение этого уравнения для времен t ≥ 0 с , предполагая V ( t = 0 ) = V ₀ это:

$${\begin{aligned}V(t)&=V_{0}e^{-t/\tau }+{\frac {Ae^{-t/\tau }}{\tau }}\int _{0}^{t}\,dt'\ e^{t'/\tau }e^{j\omega t'}\\[1ex]&=V_{0}e^{-t/\tau }+{\frac {\frac {1}{\tau }}{j\omega +{\frac {1}{\tau }}}}A\left(e^{j\omega t}-e^{-t/\tau }\right).\end{aligned}}$$

В течение длительного времени затухающие экспоненты становятся незначительными, и стационарное решение или долговременное решение имеет вид:

$$V_{\infty }(t)={\frac {1/\tau }{j\omega +1/\tau }}Ae^{j\omega t}.$$

Величина этого ответа: $$|V_{\infty }(t)|=A{\frac {1}{\tau \left(\omega ^{2}+(1/\tau )^{2}\right)^{1/2}}}=A{\frac {1}{\sqrt {1+(\omega \tau )^{2}}}}.$$По соглашению, полоса пропускания этой системы — это частота, где | В _∞ | ² падает до половины значения, или где ωτ = 1 . Это обычное соглашение о полосе пропускания , определяемое как диапазон частот, в котором мощность падает менее чем наполовину (максимум –3 дБ). Используя частоту в герцах, а не радианах/с ( ω = 2 πf ):

$$f_{\mathrm {3dB} }={\frac {1}{2\pi \tau }}.$$

Обозначение f _3dB связано с выражением мощности в децибелах и наблюдением, что половинная мощность соответствует падению значения | В _∞ | на коэффициент 1/2 или на 3 децибела.

Таким образом, постоянная времени определяет пропускную способность этой системы.

Переходный процесс с произвольными начальными условиями

Переходная реакция системы для двух разных начальных значений V ₀ , одного выше конечного значения и одного при нуле. Долговременный отклик является константой V _∞ . Ось времени в единицах постоянной времени $\tau$.

Предположим, что принудительная функция выбрана в качестве входного шага, поэтому:

$${\frac {dV}{dt}}+{\frac {1}{\tau }}V=f(t)=Au(t),$$

где u ( t ) — единичная ступенчатая функция . Общее решение этого уравнения для времени t ≥ 0 с , предполагая, что V ( t = 0) = V _0, выглядит следующим образом:

$$V(t)=V_{0}e^{-t/\tau }+A\tau \left(1-e^{-t/\tau }\right).$$

(Можно заметить, что этот отклик представляет собой предел ω → 0 вышеуказанного ответа на синусоидальный входной сигнал.)

Долгосрочное решение не зависит от времени и начальных условий: $$V_{\infty }=A\tau .$$

Постоянная времени остается неизменной для одной и той же системы независимо от начальных условий. Проще говоря, система приближается к своему окончательному, установившемуся состоянию с постоянной скоростью, независимо от того, насколько близко она находится к этому значению в любой произвольной начальной точке.

Например, рассмотрим электродвигатель, запуск которого хорошо моделируется системой LTI первого порядка. Предположим, что при запуске из состояния двигателя двигатель принимает ⁠ 1/8 мин ⁠ . секунды для достижения 63% номинальной скорости в 100 об/мин или 63 об/мин — недостаток в 37 об/ Тогда окажется, что после следующего ⁠ 1/8 . ⁠ За секунды двигатель ускорился еще на 23 об/мин, что составляет 63% от разницы в 37 об/мин Это доводит его до 86 об/мин — все еще на 14 об/мин ниже. После третьего За 1/8 мин секунды . двигатель наберет дополнительные 9 об/мин (63% от разницы в 14 об/мин), что соответствует 95 об/

Фактически, при любой начальной скорости s ≤ 100 об/мин ⁠ 1/8 ) ⁠ 0,63 × секунды спустя этот конкретный двигатель наберет дополнительные (100 − с об/мин.

Примеры

Постоянные времени в электрических цепях

Переходная характеристика напряжения конденсатора.

Переходная характеристика напряжения индуктора.

В цепи RL, состоящей из одного резистора и катушки индуктивности, постоянная времени $\tau$ (в секундах ) $$\tau ={\frac {L}{R}}$$

где R — сопротивление (в Омах ), а L — индуктивность (в генри ).

Аналогично, в RC-цепи , состоящей из одного резистора и конденсатора, постоянная времени $\tau$ (в секундах): $$\tau =RC$$

где R — сопротивление (в Омах ), а C — емкость (в фарадах ).

Электрические цепи часто более сложны, чем эти примеры, и могут иметь несколько постоянных времени (некоторые примеры см. в разделе « Переходная характеристика и разделение полюсов »). В случае наличия обратной связи система может демонстрировать нестабильные, возрастающие колебания. Кроме того, физические электрические цепи редко являются по-настоящему линейными системами, за исключением возбуждений с очень низкой амплитудой; однако широко используется приближение линейности.

В цифровых электронных схемах еще одна мера - FO4 часто используется . Это можно преобразовать в единицы постоянной времени с помощью уравнения $5\tau ={\text{FO4}}$.

Термическая постоянная времени

Постоянные времени являются особенностью анализа сосредоточенных систем (метода анализа сосредоточенной мощности) для тепловых систем, используемого, когда объекты охлаждаются или нагреваются равномерно под влиянием конвективного охлаждения или нагревания . При этом передача тепла от тела к окружающей среде в данный момент времени пропорциональна разности температур тела и окружающей среды:

$$F=hA_{s}\left(T(t)-T_{a}\right),$$

где h — коэффициент теплопередачи , а As _— площадь поверхности, T — температурная функция, т. е. T ( t ) — температура тела в момент времени t , а T _a — постоянная температура окружающей среды. Положительный знак указывает на то, что F является положительным, когда тепло покидает тело, поскольку его температура выше температуры окружающей среды ( F — поток наружу). Поскольку тепло теряется в окружающую среду, эта передача тепла приводит к падению температуры тела, определяемой:

$$\rho c_{p}V{\frac {dT}{dt}}=-F,$$

где ρ = плотность, c _p = удельная теплоемкость и V – объем тела. Знак минус указывает на падение температуры при передаче тепла наружу от тела (т. е. при F > 0). Приравнивая эти два выражения для теплопередачи,

$$\rho c_{p}V{\frac {dT}{dt}}=-hA_{s}\left(T(t)-T_{a}\right).$$

Очевидно, что это система LTI первого порядка, которую можно представить в виде:

$${\frac {dT}{dt}}+{\frac {1}{\tau }}T={\frac {1}{\tau }}T_{a},$$

с

$$\tau ={\frac {\rho c_{p}V}{hA_{s}}}.$$

Другими словами, большие массы ρV с более высокими теплоемкостями c _p приводят к более медленному изменению температуры (большая постоянная времени τ ), а большие площади поверхности A _s с большей теплоотдачей h приводят к более быстрому изменению температуры (меньшая постоянная времени τ ).

Сравнение с вводным дифференциальным уравнением предполагает возможное обобщение на случай изменяющихся во времени температур окружающей среды T _a . Однако, сохраняя простой пример с постоянной средой, подставляя переменную Δ T ≡ ( T - T _a ), можно найти:

$${\frac {d\Delta T}{dt}}+{\frac {1}{\tau }}\Delta T=0.$$

Говорят, что системы, для которых охлаждение удовлетворяет приведенному выше экспоненциальному уравнению, удовлетворяют закону охлаждения Ньютона . Решение этого уравнения предполагает, что в таких системах разница между температурой системы и ее окружения Δ T как функция времени t определяется выражением:

$\Delta T(t)=\Delta T_{0}e^{-t/\tau },$

где Δ T ₀ — начальная разница температур в момент времени t = 0. Другими словами, тело принимает ту же температуру, что и окружающая среда, с экспоненциально медленной скоростью, определяемой постоянной времени.

Постоянные времени в биофизике

В возбудимой клетке, такой как мышца или нейрон , постоянная времени мембранного потенциала $\tau$ является $$\tau =r_{m}c_{m}$$

где r _m — сопротивление мембраны, а c _m — емкость мембраны.

Сопротивление мембраны является функцией количества открытых ионных каналов , а емкость — функцией свойств липидного бислоя .

Постоянная времени используется для описания подъема и падения мембранного напряжения, где подъем описывается выражением $$V(t)=V_{\textrm {max}}\left(1-e^{-t/\tau }\right)$$

и падение описывается $$V(t)=V_{\textrm {max}}e^{-t/\tau }$$

где напряжение указано в милливольтах, время — в секундах, а $\tau$ это в секундах.

V _max определяется как максимальное изменение напряжения от потенциала покоя , где $$V_{\textrm {max}}=r_{m}I$$

где r _m — сопротивление мембраны, а I — мембранный ток.

Настройка для t = $\tau$ для подъема устанавливают V ( t ) равным 0,63 В _max . Это означает, что постоянная времени — это время, прошедшее после 63 % от V _max. достижения

Настройка для t = $\tau$ для падения устанавливает V ( t ) равным 0,37 В _max , что означает, что константа времени — это время, прошедшее после того, как оно упало до 37% от V _max .

Чем больше постоянная времени, тем медленнее нарастает или падает потенциал нейрона. Большая постоянная времени может привести к временному суммированию или алгебраическому суммированию повторяющихся потенциалов. Короткая постоянная времени скорее создает детектор совпадений посредством пространственного суммирования .

Экспоненциальный распад

Дополнительная информация: Экспоненциальный распад.

При экспоненциальном распаде , например, радиоактивного изотопа, постоянную времени можно интерпретировать как среднее время жизни . Период полураспада T _HL или T _1/2 связан с константой экспоненциального распада. $\tau$ к $$T_{1/2}=T_{\text{HL}}=\tau \ln 2.$$Обратная константа времени называется постоянной затухания и обозначается $\lambda =1/\tau$.

Метеорологические датчики

Постоянная времени — это количество времени, которое требуется метеорологическому датчику, чтобы отреагировать на быстрое изменение показателя, и до тех пор, пока он не начнет измерять значения в пределах допуска точности, обычно ожидаемого от датчика.

Чаще всего это касается измерений температуры, температуры точки росы, влажности и давления воздуха. радиозонды Особенно страдают из-за их быстрого увеличения высоты.

См. также

• Постоянная времени RC
• Частота среза
• Экспоненциальный распад
• Компенсатор опережения-запаздывания
• Постоянная длина
• Время подъема
• Время падения
• Частотная характеристика
• Импульсный отклик
• Шаговый отклик
• Время урегулирования

Внешние ссылки

• Преобразование постоянной времени τ в частоту среза fc и наоборот
• Все о схемах - Расчеты напряжения и тока
• Энергетическая и тепловая постоянная времени зданий