Гемореология

Гемореология , также пишется как гемореология ( гемо от греческого αἷμα, haima « кровь »; и реология от греческого ῥέω rhéō , « поток » и -λoγία, -logia «изучение»), или реология крови — это изучение свойств текучести. крови и ее элементов плазмы и клеток . тканей Правильная перфузия свойства крови может произойти только тогда, когда реологические находятся в пределах определенных уровней. Изменения этих свойств играют важную роль в болезненных процессах. ^{[ 1 ]} крови Вязкость определяется вязкостью плазмы, гематокритом (объемная доля эритроцитов, составляющих 99,9% клеточных элементов) и механическими свойствами эритроцитов . Эритроциты обладают уникальным механическим поведением, которое можно рассматривать как деформируемость эритроцитов и агрегацию эритроцитов . ^{[ 2 ]} Из-за этого кровь ведет себя как неньютоновская жидкость . Таким образом, вязкость крови зависит от скорости сдвига . Кровь становится менее вязкой при высоких скоростях сдвига, как при повышенном потоке, например, во время физических упражнений или в пиковую систолу . Следовательно, кровь представляет собой разжижающуюся при сдвиге жидкость. И наоборот, вязкость крови увеличивается, когда скорость сдвига снижается при увеличении диаметра сосуда или при низком потоке, например, после обструкции или в диастолу . Вязкость крови также увеличивается с увеличением агрегации эритроцитов.

Вязкость крови

Вязкость крови является мерой сопротивления крови течению. Его также можно охарактеризовать как густоту и липкость крови. Это биофизическое свойство делает его решающим фактором, определяющим трение о стенки сосудов , скорость венозного возврата , работу, необходимую сердцу для перекачивания крови, а также количество кислорода, транспортируемого к тканям и органам. Эти функции сердечно-сосудистой системы напрямую связаны с сосудистым сопротивлением , преднагрузкой , постнагрузкой и перфузией соответственно. ^{[ нужна ссылка ]}

Основными детерминантами вязкости крови являются гематокрит , деформируемость эритроцитов , агрегация эритроцитов и вязкость плазмы . Вязкость плазмы определяется содержанием воды и макромолекулярными компонентами, поэтому факторами, влияющими на вязкость крови, являются концентрация белков плазмы и типы белков в плазме. ^{[ 3 ]} Тем не менее, гематокрит оказывает наиболее сильное влияние на вязкость цельной крови. Увеличение гематокрита на одну единицу может вызвать увеличение вязкости крови до 4%. ^{[ 2 ]} Эта связь становится все более чувствительной по мере увеличения гематокрита. Когда гематокрит повышается до 60 или 70%, что часто бывает при полицитемии , ^{[ 4 ]} вязкость крови может в 10 раз превышать вязкость воды, а ее течение по кровеносным сосудам значительно замедляется из-за повышенного сопротивления потоку. ^{[ 5 ]} Это приведет к снижению доставки кислорода . ^{[ 6 ]} Другие факторы, влияющие на вязкость крови, включают температуру : повышение температуры приводит к снижению вязкости. Это особенно важно при переохлаждении , когда повышение вязкости крови вызывает проблемы с кровообращением.

Клиническое значение

Многие традиционные факторы риска сердечно-сосудистых заболеваний независимо связаны с вязкостью цельной крови.

Факторы риска сердечно-сосудистых заболеваний, независимо связанные с вязкостью цельной крови ^{[ 7 ]}
Гипертония
Общий холестерин
ЛПОНП-холестерин
ЛПНП-холестерин
ЛПВП-холестерин (отрицательная корреляция)
Триглицериды
Хиломикроны
Сахарный диабет и инсулинорезистентность
Метаболический синдром
Ожирение
Курение сигарет
мужской пол
Возраст

Анемия может снизить вязкость крови, что может привести к сердечной недостаточности . ^{[ 7 ]} Кроме того, повышение вязкости плазмы коррелирует с прогрессированием заболеваний коронарных и периферических артерий . ^{[ 3 ]}^{[ 4 ]}

Нормальный уровень

В паскалях – секундах (Па·с), вязкость $\mu$ крови при 37 °C обычно составляет 3 × 10 ⁻³ до 4 × 10 ⁻³, ^{[ 8 ]} соответственно 3–4 сантипуаз (сП) в системе единиц сантиметр-грамм-секунда .

$\mu =(3\sim 4)\cdot 10^{-3}\,Pa\cdot s$

$\nu ={\frac {\mu }{\rho }}={\frac {(3\sim 4)\cdot 10^{-3}Pa\cdot s}{1.06\cdot 10^{3}{\frac {kg}{m^{3}}}}}=(2.8\sim 3.8)\cdot 10^{-6}\,{\frac {m^{2}}{s}}$ ,

где $\rho$ это плотность. Вязкость крови можно измерить с помощью вискозиметров, способных проводить измерения при различных скоростях сдвига, например, ротационного вискозиметра . ^{[ 9 ]}

Вязкоэластичность крови

Кровь представляет собой вязкоупругую жидкость, а это означает, что она обладает как вязкими, так и жидкими характеристиками. Вязкая составляющая возникает преимущественно за счет вязкости плазмы крови, а эластическая — за счет деформации эритроцитов . Когда сердце сокращается, механическая энергия передается от сердца к крови; небольшая часть энергии рассеивается за счет вязкости суспензии , другая часть сохраняется в виде упругой энергии в красных кровяных тельцах, а оставшаяся энергия используется для управления кровообращением и, таким образом, преобразуется в кинетическую энергию . Вязкоупругие жидкости составляют более широкий класс жидкостей, называемый неньютоновскими жидкостями .

Эритроциты занимают около половины объема крови и обладают эластическими свойствами. Это эластичное свойство является основным фактором, способствующим вязкоупругому поведению крови. Большой объемный процент эритроцитов при нормальном уровне гематокрита оставляет мало места для движения и деформации клеток без взаимодействия с соседней клеткой. Расчеты показали, что максимальный объемный процент эритроцитов без деформации составляет 58%, что находится в пределах нормально встречающихся уровней. ^{[ 10 ]} Из-за ограниченного пространства между эритроцитами очевидно, что для кровотока ключевую роль будет играть значительное межклеточное взаимодействие. Это взаимодействие и тенденция клеток к агрегации вносят основной вклад в вязкоупругое поведение крови. Деформация и агрегация эритроцитов также сочетаются с вызванными потоком изменениями в расположении и ориентации, что является третьим основным фактором их вязкоупругого поведения. ^{[ 11 ]}^{[ 12 ]} Другими факторами, способствующими вязкоупругим свойствам крови, являются вязкость плазмы, состав плазмы, температура и скорость потока или скорость сдвига. Вместе эти факторы делают человеческую кровь вязкоупругой , неньютоновской и тиксотропной . ^{[ 13 ]}

Когда эритроциты находятся в состоянии покоя или при очень малых скоростях сдвига, они имеют тенденцию агрегироваться и складываться вместе энергетически выгодным образом. Притяжение объясняется заряженными группами на поверхности клеток и наличием фибриногена и глобулинов. ^{[ 14 ]} Эта агрегированная конфигурация представляет собой расположение ячеек с наименьшей степенью деформации. При очень низких скоростях сдвига в вязкоупругих свойствах крови преобладает агрегация, а деформируемость клеток относительно незначительна. По мере увеличения скорости сдвига размер агрегатов начинает уменьшаться. При дальнейшем увеличении скорости сдвига клетки будут перестраиваться и ориентироваться, создавая каналы для прохождения плазмы и скольжения клеток. В этом диапазоне скоростей сдвига от низкой до средней клетки покачиваются относительно соседних клеток, обеспечивая поток. Влияние агрегативных свойств на вязкоупругость уменьшается и начинает возрастать влияние деформируемости эритроцитов. Когда скорость сдвига становится большой, эритроциты растягиваются или деформируются и выравниваются по потоку. Образуются слои клеток, разделенные плазмой, и поток теперь приписывается слоям клеток, скользящим по слоям плазмы. Слой клеток обеспечивает более легкий поток крови, что приводит к снижению вязкости и эластичности. В вязкоупругости крови преобладает деформируемость эритроцитов.

Модель Максвелла

Модель Максвелла касается жидкостей Максвелла или материала Максвелла . Материал в модели Максвелла представляет собой жидкость , что означает, что он учитывает свойства непрерывности для консервативных уравнений: жидкости представляют собой подмножество фаз материи и включают жидкости, газы, плазму и, в некоторой степени, твердые пластмассы. Модель Максвелла создана для оценки локальных консервативных значений вязкоупругости с помощью глобальной меры в интегральном объеме модели, которая может быть перенесена на различные ситуации потока. Кровь представляет собой сложный материал, в котором различные клетки, такие как эритроциты, находятся в плазме неоднородно. Их размер и форма также неправильны, поскольку они не являются идеальными сферами. Кроме того, усложняя форму объема крови, эритроциты не одинаково распределяются в объеме образца крови, поскольку они мигрируют с градиентами скорости в направлении к областям с наибольшей скоростью, что вызывает знаменитое представление эффекта Фареуса-Линдквиста , агрегируя или разделяя в описанных оболочках или пробковых потоках. от Терстона. ^{[ 15 ]} Как правило, модель Максвелла, описанная ниже, единообразно рассматривает материал (однородный синий цвет) как идеально распределенные частицы, жидкие повсюду в объеме (синий цвет), но Терстон показывает, что пакеты красных клеток, пробки, больше присутствуют в области высоких скоростей. , если y — направление высоты на рисунке модели Максвелла, ( y ~ 0) имеется слой свободных ячеек, ~ H) и в области более низких скоростей ( y что означает, что фаза плазменной жидкости, которая деформируется в соответствии с моделью Максвелла, напряжена в соответствии с внутренними условиями. подкладки, совершенно выходящие за рамки аналитической модели Максвелла. ^{[ нужна ссылка ]}

Теоретически жидкость в модели Максвелла ведет себя точно так же в любой другой геометрии потока, например, в трубах, вращающихся ячейках или в состоянии покоя. Но на практике свойства крови различаются в зависимости от геометрии, и кровь оказалась неподходящим материалом для изучения как жидкости в здравом смысле. Итак, модель Максвелла дает тенденции, которые должны быть реализованы в реальной ситуации, а затем модель Терстона. ^{[ 15 ]} в сосуде относительно распределения клеток в оболочках и пробковом течении. ^{[ нужна ссылка ]}

Если рассматривать небольшой кубический объем крови, на который действуют силы сердечного ритма и силы сдвига от границ. Изменение формы куба будет иметь 2 компонента:

Эластическая деформация, поддающаяся восстановлению и сохраняющаяся в структуре крови.
Проскальзывание, которое связано с непрерывным подводом вязкой энергии .

Когда сила будет снята, куб частично восстановится. Упругая деформация обратима, а проскальзывание — нет. Это объясняет, почему упругая часть заметна только при нестационарном потоке. В установившемся потоке проскальзывание будет продолжать увеличиваться, и при измерении не меняющейся во времени силы вклад упругости будет пренебрегаться.

Рисунок 1 можно использовать для расчета следующих параметров, необходимых для оценки крови при приложении силы.

Напряжение сдвига:

\tau ={\frac {F}{A}}

Сдвиговая деформация:

\gamma ={\frac {D}{H}}

Скорость сдвига:

{\dot {\gamma }}={\frac {V}{H}}

Синусоидальный изменяющийся во времени поток используется для имитации пульсации сердца. Вязкоэластичный материал, подвергающийся изменяющемуся во времени потоку, приведет к изменению фазы между $\tau$ и $\gamma$ в лице $\phi$ . Если $\phi =0$ Материал является чисто упругим, поскольку напряжение и деформация находятся в фазе, поэтому реакция одного на другое происходит мгновенно. Если $\phi$ = 90°, материал является чисто вязким, поскольку деформация отстает от напряжения на 90 градусов. Вязкоэластичный материал будет где-то между 0 и 90 градусами.

Синусоидальное изменение во времени пропорционально $e^{i\omega t}$ . Следовательно, размерное и фазовое соотношение между напряжением, деформацией и скоростью сдвига описывается с использованием этого соотношения и радианской частоты: $\omega =2\pi f$ были $f$ это частота в Герцах .

Напряжение сдвига:

\tau ^{*}=\tau e^{-i\phi }

Сдвиговая деформация:

\gamma ^{*}=\gamma e^{-i{\frac {\pi }{2}}}

Скорость сдвига:

{\dot {\gamma }}^{*}={\dot {\gamma }}e^{-i0}

Компоненты комплексного касательного напряжения можно записать как:

\tau ^{*}=\tau '-i\tau ''

Где $\tau '$ вязкое напряжение и $\tau ''$ – упругое напряжение. Комплексный коэффициент вязкости $\eta ^{*}$ можно найти, взяв отношение комплексного напряжения сдвига и комплексной скорости сдвига: ^{[ 16 ]}

\eta ^{*}={\frac {\tau ^{*}}{{\dot {\gamma }}^{*}}}=({\frac {\tau '}{\dot {\gamma }}}+i{\frac {\tau ''}{\dot {\gamma }}})=\eta '+i\eta ''

Аналогичным образом, комплексный динамический модуль G можно получить, взяв отношение комплексного напряжения сдвига к комплексной деформации сдвига.

G={\frac {\tau ^{*}}{\gamma ^{*}}}=({\frac {\tau ''}{\gamma }}+i{\frac {\tau '}{\gamma }})

Связывая уравнения с общими вязкоупругими терминами, мы получаем модуль упругости G' и модуль потерь G".

G=G'+iG''

Модель вязкоупругого материала Максвелла обычно используется для представления вязкоупругих свойств крови . В нем используется чисто вязкостный демпфер и чисто упругая пружина, соединенные последовательно. Анализ этой модели дает комплексную вязкость с точки зрения постоянной демпфера и жесткости пружины.

\eta ^{*}={\frac {\eta _{dash}}{1+i\omega ({\frac {\eta _{dash}}{E_{spring}}})}}=\eta '-i\eta ''

Модель Олдройд-Б

Одной из наиболее часто используемых конститутивных моделей вязкоупругости крови является модель Олдройда-Б. Существует несколько вариантов неньютоновской модели Олдройда-Б, характеризующей поведение истончения при сдвиге из-за агрегации и дисперсии эритроцитов при низкой скорости сдвига. Здесь мы рассматриваем трехмерную модель Олдройда-Б в сочетании с уравнением количества движения и тензором полного напряжения. ^{[ 17 ]} Используется неньютоновский поток, который гарантирует, что вязкость крови $\mu (h,d)$ является функцией диаметра сосуда d и гематокрита h. В модели Олдройда-Б связь между тензором касательных напряжений B и тензором ориентационных напряжений A определяется выражением:

$S+\gamma \left[{\frac {DS}{Dt}}-\Delta V\cdot S-S\cdot {(\Delta V)}^{T}\right]=\mu (h,d)\left[B+\gamma \left({\frac {DB}{Dt}}-\Delta V\cdot B-B\cdot {(\Delta V)}^{T}\right)\right]-gA+C_{1}\left(gA-{\frac {C_{2}I}{\mu (h,d)^{2}}}\right)$

где D/Dt — производная материала, V — скорость жидкости, C1, C2, g, $\gamma$ являются константами. S и B определяются следующим образом:

S=\mu B+gA

B=\Delta V+(\Delta V)^{T}

Вязкоэластичность эритроцитов

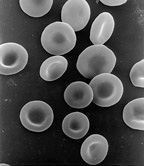
Эритроциты подвергаются интенсивной механической стимуляции как со стороны кровотока, так и со стороны стенок сосудов, и их реологические свойства важны для эффективности выполнения ими биологических функций в микроциркуляции. ^{[ 18 ]} Было показано, что эритроциты сами по себе обладают вязкоупругими свойствами. Существует несколько методов исследования механических свойств эритроцитов, таких как:

аспирация микропипеткой ^{[ 19 ]}
микроотступ
оптический пинцет
испытания на высокочастотную электрическую деформацию

Эти методы позволили охарактеризовать деформируемость эритроцитов с точки зрения сдвига, изгиба, модулей расширения площади и времени релаксации. ^{[ 20 ]} Однако им не удалось изучить вязкоупругие свойства. Были реализованы и другие методы, такие как фотоакустические измерения. В этом методе используется одноимпульсный лазерный луч для генерации фотоакустического сигнала в тканях и измеряется время затухания сигнала. Согласно теории линейной вязкоупругости, время затухания равно соотношению вязкоупругости, и поэтому можно получить характеристики вязкоупругости эритроцитов. ^{[ 21 ]}

Другой экспериментальный метод, используемый для оценки вязкоупругости, заключался в использовании ферромагнетических шариков, прикрепленных к поверхности клеток. Затем к магнитному шарику прикладывают силы с помощью оптической магнитно-скручивающей цитометрии, что позволило исследователям изучить зависящие от времени реакции эритроцитов. ^{[ 22 ]}

$T_{s}(t)$ представляет собой механический крутящий момент на единицу объема борта (единицы напряжения) и определяется по формуле:

T_{s}(t)=cH\cos \theta

где H — приложенное магнитное скручивающее поле, ${\theta }$ - угол магнитного момента шарика относительно исходного направления намагничивания, а c - постоянная шарика, которая определяется в ходе экспериментов, проводимых путем помещения шарика в жидкость известной вязкости и приложения скручивающего поля.

Комплексный динамический модуль G можно использовать для представления зависимости между осциллирующим напряжением и деформацией:

G=G'+iG''

где $G'$ модуль упругости и $G''$ модуль потерь :

G'={\frac {\sigma _{0}}{\varepsilon _{0}}}\cos \phi

G''={\frac {\sigma _{0}}{\varepsilon _{0}}}\sin \phi

где $\sigma _{0}$ и $\varepsilon _{0}$ - амплитуды напряжений и деформаций и $\phi$ фазовый сдвиг между ними.

Рисунок 3. График зависимости крутящего момента от смещения, показывающий вязкоупругое поведение.

Из приведенных выше соотношений компоненты комплексного модуля определяются из петли, которая создается путем сравнения изменения крутящего момента с изменением во времени, которая образует петлю при графическом представлении. Пределы $T_{s}(t)$ - петля d(t) и площадь A, ограниченная $T_{s}(t)$ - В расчетах используется петля d(t), которая представляет собой рассеяние энергии за цикл. Фазовый угол $\phi$ , модуль упругости G' и модуль потерь G тогда станут:

\phi =\sin ^{-1}{\frac {4A}{\pi \Delta T_{s}\Delta d}}

G'={\frac {\Delta T_{s}}{\Delta d}}\cos \phi

G''={\frac {\Delta T_{s}}{\Delta d}}\sin \phi ={\frac {4A}{\pi \omega \Delta d^{2}}}

где d — перемещение.

Гистерезис, показанный на рисунке 3, представляет собой вязкоупругость, присутствующую в эритроцитах. Неясно, связано ли это с мембранными молекулярными колебаниями или метаболической активностью, контролируемой внутриклеточными концентрациями АТФ . Необходимы дальнейшие исследования, чтобы полностью изучить это взаимодействие и пролить свет на основные характеристики вязкоупругой деформации эритроцитов.

Влияние кровеносных сосудов

При рассмотрении вязкоупругого поведения крови in vivo необходимо также учитывать влияние артерий , капилляров и вен . Вязкость крови оказывает основное влияние на кровоток в крупных артериях, тогда как эластичность, заключающаяся в упругой деформируемости эритроцитов, оказывает основное влияние на артериолы и капилляры. ^{[ 23 ]} Понимание распространения волн в стенках артерий, местной гемодинамики и градиента напряжения сдвига стенок важно для понимания механизмов сердечно-сосудистой функции. Стенки артерий анизотропны и неоднородны, состоят из слоев с различными биомеханическими характеристиками, что затрудняет понимание механических влияний, которые артерии оказывают на кровоток. ^{[ 24 ]}

Медицинские причины для лучшего понимания

С медицинской точки зрения становится очевидной важность изучения вязкоупругих свойств крови. С развитием сердечно-сосудистых протезов, таких как сердечные клапаны и насосы крови, требуется понимание пульсирующего потока крови в сложной геометрии. Несколькими конкретными примерами являются эффекты вязкоупругости крови и ее значение для испытаний пульсирующих насосов крови. ^{[ 25 ]} Были документально подтверждены сильные корреляции между вязкоэластичностью крови и региональным и глобальным мозговым кровотоком во время искусственного кровообращения. ^{[ 26 ]}

Это также проложило путь к разработке аналога крови для изучения и испытаний протезов. Классический аналог глицерина и воды хорошо отображает вязкость и инерционные эффекты, но ему не хватает эластичных свойств настоящей крови. Одним из таких аналогов крови является водный раствор ксантановой камеди и глицерина, разработанный для соответствия как вязким, так и эластичным компонентам комплексной вязкости крови. ^{[ 27 ]}

Нормальные эритроциты деформируются, но многие состояния, такие как серповидноклеточная анемия , снижают их эластичность, что делает их менее деформируемыми. Эритроциты с пониженной деформируемостью имеют увеличивающееся сопротивление потоку, что приводит к увеличению агрегации эритроцитов и снижению насыщения кислородом, что может привести к дальнейшим осложнениям. Присутствие клеток с пониженной деформируемостью, как в случае серповидноклеточной анемии, имеет тенденцию ингибировать образование слоев плазмы, и путем измерения вязкоэластичности можно определить степень ингибирования. ^{[ 28 ]}

История

В ранних теоретических работах кровь рассматривалась как неньютоновская вязкая жидкость. Первоначальные исследования оценивали кровь при постоянном потоке, а затем при использовании осциллирующего потока. ^{[ 29 ]} Профессор Джордж Б. Терстон из Техасского университета впервые представил идею о том, что кровь является вязкоупругой в 1972 году. Предыдущие исследования, в которых изучалась кровь в устойчивом потоке, показали незначительные эластические свойства, поскольку эластичный режим сохраняется в крови во время начала кровотока и поэтому его присутствие скрыто, когда поток достигает устойчивого состояния. В ранних исследованиях использовались свойства, обнаруженные в установившемся потоке, для получения свойств для ситуаций нестационарного потока. ^{[ 30 ]}^{[ 31 ]} Развитие медицинских процедур и устройств потребовало лучшего понимания механических свойств крови. ^{[ нужна ссылка ]}

Определяющие уравнения

Взаимосвязь между напряжением сдвига и скоростью сдвига для крови должна быть определена экспериментально и выражена определяющими уравнениями . Учитывая сложное макрореологическое поведение крови, неудивительно, что одно уравнение не может полностью описать влияние различных реологических переменных (например, гематокрита , скорости сдвига). Таким образом, существует несколько подходов к определению этих уравнений, некоторые из которых являются результатом аппроксимации экспериментальных данных, а другие основаны на конкретной реологической модели.

Модель ньютоновской жидкости , имеющая постоянную вязкость при всех скоростях сдвига. Этот подход справедлив для высоких скоростей сдвига ( ${\dot {\gamma }}>700\,s^{-1}$ ), где диаметр сосуда намного больше, чем клетки крови. ^{[ 32 ]}
Модель жидкости Бингама учитывает агрегацию эритроцитов при низких скоростях сдвига. Следовательно, он действует как упругое твердое тело при пороговом уровне напряжения сдвига, известного как предел текучести .
Модель Эйнштейна, где η ₀ — ньютоновская вязкость суспендирующей жидкости, «k» — константа, зависящая от формы частиц, а H — объемная доля суспензии, занятая частицами. Это уравнение применимо для суспензий с низкой объемной долей частиц. Эйнштейн показал k=2,5 для сферических частиц.

\mu _{a}={{\mu _{0}}\times {(1+kH)}}

Модель Кассона, где «a» и «b» являются константами; при очень низких скоростях сдвига b — напряжение текучести при сдвиге. Однако для крови экспериментальные данные не могут быть подогнаны ко всем скоростям сдвига только с одним набором констант «a» и «b», тогда как достаточно хорошее соответствие возможно, если применить уравнение к нескольким диапазонам скоростей сдвига и получить, таким образом, несколько наборов констант.

{\tau }^{0.5}={{a}{|\gamma |}^{0.5}+b^{0.5}}

Модель Кемады, где k ₀ , k _∞ и γ _c — константы. Это уравнение точно соответствует данным крови в очень широком диапазоне скоростей сдвига.

\mu _{a}={{\mu _{0}}{{(1-0.5kH)}^{-2}}}

k={{k_{0}+k_{\inf }{\gamma ^{0.5}}_{r}} \over {1+{\gamma ^{0.5}}_{r}}}

\gamma _{r}={{\gamma } \over {\gamma _{c}}}

Другие характеристики

Эффект Фореуса

Открытие о том, что при постоянном течении крови в трубках диаметром менее 300 микрометров средний гематокрит крови в трубке меньше гематокрита крови в резервуаре, питающем трубку, известно как эффект Фареуса. Этот эффект возникает на длине входа концентрации в трубку, при которой эритроциты движутся к центральной части трубки по мере движения вниз по течению. По оценкам, эта длина входа равна расстоянию, которое кровь проходит за четверть секунды для крови, где агрегация эритроцитов незначительна, а диаметр сосуда превышает примерно 20 микрометров. ^{[ 1 ]}

Эффект Фареуса-Линдквиста

Поскольку характерный размер канала потока приближается к размеру частиц в суспензии; следует ожидать, что простая континуальная модель подвески окажется неприменимой. Часто этот предел применимости модели континуума начинает проявляться при характерных размерах каналов, которые примерно в 30 раз превышают диаметр частиц: в случае крови с характерным размером эритроцитов 8 мкм кажущийся отказ происходит на расстоянии около 300 микрометров. . Это было продемонстрировано Фореусом и Линдквистом, которые обнаружили, что кажущаяся вязкость крови зависит от диаметра трубки для диаметров 300 микрометров и меньше, когда через трубку текла кровь с постоянным гематокритом из хорошо перемешиваемого резервуара. Открытие о том, что для небольших трубок диаметром менее 300 микрометров и для более высоких скоростей потока, которые не допускают заметной агрегации эритроцитов, эффективная вязкость крови зависит от диаметра трубок, известно как эффект Фареуса-Линдквиста. ^{[ 1 ]}

См. также

Альфред Л. Копли
Кровавый молот
Биореология , изучение свойств течения (реологии) биологических жидкостей.
Гемодинамика
Синдром гипервязкости
Rouleaux — это конфигурация, которую принимают агрегаты RBC.

Ссылки

^ Jump up to: ^а ^б ^с Баскурт, ок; Хардеман М; Рэмплинг МВт; Мейзельман HJ (2007). Справочник по гемореологии и гемодинамике . Амстердам, Нидерланды: IOS Press. стр. 455 . ISBN 978-1586037710 . ISSN 0929-6743 . {{cite book}}: |journal= игнорируется ( помогите )
^ Jump up to: ^а ^б Баскурт ОК, Мейзельман Х.Ю. (2003). «Реология крови и гемодинамика». Семинары по тромбозам и гемостазу . 29 (5): 435–450. дои : 10.1055/s-2003-44551 . ПМИД 14631543 . S2CID 17873138 .
^ Jump up to: ^а ^б Кесмарки Г., Кеньерес П., Рабай М., Тот К. (2008). «Вязкость плазмы: забытая переменная» . Клин. Гемореол. Микроциркулятор . 39 (1–4): 243–6. дои : 10.3233/CH-2008-1088 . ПМИД 18503132 . Архивировано из оригинала 14 мая 2016 г.
^ Jump up to: ^а ^б Теффери А. (май 2003 г.). «Современный подход к диагностике и лечению истинной полицитемии». Курс. Гематол. Представитель . 2 (3): 237–41. ПМИД 12901345 .
^ Ленц С., Ребел А., Вашке К.Ф., Келер Р.К., Фрич Т. (2008). «Вязкость крови модулирует перфузию тканей: иногда и где-то» . Трансфус Альтерн Трансфус Мед . 9 (4): 265–272. дои : 10.1111/j.1778-428X.2007.00080.x . ПМК 2519874 . ПМИД 19122878 .
^ Квон О., Кришнамурти М., Чо Й.И., Санкович Дж.М., Банерджи Р.К. (февраль 2008 г.). «Влияние вязкости крови на транспорт кислорода в остаточной стенозированной артерии после ангиопластики». Журнал биомеханической инженерии . 130 (1): 011003. дои : 10.1115/1.2838029 . ПМИД 18298179 . S2CID 40266740 .
^ Jump up to: ^а ^б Чон, Сыль Ки; и др. (апрель 2010 г.). «Сердечно-сосудистые риски коррекции анемии препаратами, стимулирующими эритроциты: нужно ли контролировать вязкость крови для оценки риска?». Сердечно-сосудистые препараты и терапия . 24 (2): 151–60. дои : 10.1007/s10557-010-6239-7 . ПМИД 20514513 . S2CID 6366788 .
^ Элерт, Гленн (27 ноября 2021 г.). «Вязкость» . Гиперучебник по физике – через Physics.info.
^ Баскурт О.К., Бойнард М., Кокелет Г.К. и др. (2009). «Новые рекомендации по гемореологическим лабораторным методам» . Клиническая гемореология и микроциркуляция . 42 (2): 75–97. дои : 10.3233/CH-2009-1202 . ПМИД 19433882 . S2CID 15866651 .
^ А. Бертон (1965). Физиология и биофизика кровообращения . Чикаго (США): Year Book Medical Publisher Inc., с. 53.
^ Г. Терстон; Нэнси М. Хендерсон (2006). «Влияние геометрии потока на вязкоупругость крови». Биореология . 43 (6): 729–746. ПМИД 17148856 .
^ Г. Терстон (1989). «Высвобождение плазмы - теория наслоения клеток для кровотока». Биореология . 26 (2): 199–214. дои : 10.3233/бир-1989-26208 . ПМИД 2605328 .
^ Г. Терстон (1979). «Реологические параметры вязкости, вязкоупругости и тиксотропии крови». Биореология . 16 (3): 149–162. дои : 10.3233/бир-1979-16303 . ПМИД 508925 .
^ Л. Пиркл и Т. Боднар, Численное моделирование кровотока с использованием обобщенной модели Олдройда-Б, Европейская конференция по вычислительной гидродинамике, 2010 г.
^ Jump up to: ^а ^б Терстон Г., Хендерсон Нэнси М. (2006). «Влияние геометрии потока на вязкоупругость крови». Биореология . 43 (6): 729–746. ПМИД 17148856 .
^ Т. Как, Достижения в гемодинамике и гемореологии Том. 1, JAI Press LTD., 1996, 1-32.
^ Р. Берд, Р. Армстронг, О. Хассагер, Динамика полимерных жидкостей; Механик жидкости, 1987, 2, 493 – 496.
^ М. Мофрад, Х. Керхер и Р. Камм, Цитоскелетная механика: модели и измерения, 2006, 71-83.
^ В. Лубарда и А. Марцани, Вязкоупругая реакция тонких мембран при применении. к эритроцитам, Acta Mechanica, 2009, 202, 1–16.
^ Д. Федосов, Б. Касвелл и Г. Карниадакис, Модель крупнозернистых эритроцитов с точными механическими свойствами, реологией и динамикой, 31-я ежегодная международная конференция IEEE EMBS, Миннеаполис, Миннесота, 2009 г.
^ Дж. Ли, З. Тан, Ю. Ся, Ю. Лу и Г. Ли, Характеристика вязкоупругих клеток с использованием фотоакустических измерений, Журнал прикладной физики, 2008, 104
^ М. Маринкович, К. Тернер, Дж. Батлер, Дж. Фредберг и С. Суреш, Вязкоэластичность эритроцитов человека, Американский журнал физиологии. Клеточная физиология 2007, 293, 597-605.
^ А. Юндар, В. Вон и Дж. Калхун, Влияние искусственного кровообращения и глубокой гипотермической остановки кровообращения на вязкоэластичность крови и мозговой кровоток в модели неонатального поросенка, Perfusion 2000, 15, 121–128
^ С. Каник , Дж. Тамбака, Г. Гвидобони, А. Микелич, К. Хартли и Д. Розенштраух, Моделирование вязкоупругого поведения артериальных стенок и их взаимодействия с пульсирующим потоком крови, Журнал прикладной математики, 2006, 67, 164–193
^ Дж. Лонг, А. Ундар, К. Мэннинг и С. Дойч, Вязкоэластичность педиатрической крови и ее значение для тестирования пульсирующего педиатрического насоса крови, Американское общество внутренних органов, 2005, 563–566.
^ А. Ундар и В. Вон, Влияние легкого гипотермического искусственного кровообращения на вязкоэластичность крови у пациентов с аортокоронарным шунтированием, Искусственные органы 26 (11), 964–966
^ К. Брукшир и Дж. Тарбелл, Оценка прозрачной жидкости-аналога крови: водная ксантановая камедь/глицерин, Биореология, 1993, 2, 107-16.
^ Г. Терстон, Н. Хендерсон и М. Дженг, Влияние переливания эритроцитафереза на вязкоупругость серповидноклеточной крови, Клиническая гемореология и микроциркуляция 30 (2004) 61–75
^ Дж. Уомерсли, Метод расчета скорости, скорости потока и вязкого сопротивления в артериях, когда известен градиент давления, Amer. Журнал Физиол. 1955, 127, 553–563.
^ Г. Терстон, Вязкоупругость человеческой крови, Биофизический журнал, 1972, 12, 1205–1217.
^ Г. Терстон, Вязкость и вязкоупругость крови в трубках малого диаметра, Микрососудистые исследования, 1975, 11, 133-146.
^ Фунг, ЮК (1993). Биомеханика: механические свойства живых тканей (2-е изд.). Нью-Йорк, штат Нью-Йорк: Спрингер. ISBN 9780387979472 .

[handbookBaskurt-1] Jump up to: ^а ^б ^с Баскурт, ок; Хардеман М; Рэмплинг МВт; Мейзельман HJ (2007). Справочник по гемореологии и гемодинамике . Амстердам, Нидерланды: IOS Press. стр. 455 . ISBN 978-1586037710 . ISSN 0929-6743 . {{cite book}}: |journal= игнорируется ( помогите )

[Baskurt2003-2] Jump up to: ^а ^б Баскурт ОК, Мейзельман Х.Ю. (2003). «Реология крови и гемодинамика». Семинары по тромбозам и гемостазу . 29 (5): 435–450. дои : 10.1055/s-2003-44551 . ПМИД 14631543 . S2CID 17873138 .

[pmid18503132-3] Jump up to: ^а ^б Кесмарки Г., Кеньерес П., Рабай М., Тот К. (2008). «Вязкость плазмы: забытая переменная» . Клин. Гемореол. Микроциркулятор . 39 (1–4): 243–6. дои : 10.3233/CH-2008-1088 . ПМИД 18503132 . Архивировано из оригинала 14 мая 2016 г.

[pmid12901345-4] Jump up to: ^а ^б Теффери А. (май 2003 г.). «Современный подход к диагностике и лечению истинной полицитемии». Курс. Гематол. Представитель . 2 (3): 237–41. ПМИД 12901345 .

[pmid19122878-5] Ленц С., Ребел А., Вашке К.Ф., Келер Р.К., Фрич Т. (2008). «Вязкость крови модулирует перфузию тканей: иногда и где-то» . Трансфус Альтерн Трансфус Мед . 9 (4): 265–272. дои : 10.1111/j.1778-428X.2007.00080.x . ПМК 2519874 . ПМИД 19122878 .

[pmid18298179-6] Квон О., Кришнамурти М., Чо Й.И., Санкович Дж.М., Банерджи Р.К. (февраль 2008 г.). «Влияние вязкости крови на транспорт кислорода в остаточной стенозированной артерии после ангиопластики». Журнал биомеханической инженерии . 130 (1): 011003. дои : 10.1115/1.2838029 . ПМИД 18298179 . S2CID 40266740 .

[Jeong,_Seul-Ki,_et_al._151–60-7] Jump up to: ^а ^б Чон, Сыль Ки; и др. (апрель 2010 г.). «Сердечно-сосудистые риски коррекции анемии препаратами, стимулирующими эритроциты: нужно ли контролировать вязкость крови для оценки риска?». Сердечно-сосудистые препараты и терапия . 24 (2): 151–60. дои : 10.1007/s10557-010-6239-7 . ПМИД 20514513 . S2CID 6366788 .

[8] Элерт, Гленн (27 ноября 2021 г.). «Вязкость» . Гиперучебник по физике – через Physics.info.

[9] Баскурт О.К., Бойнард М., Кокелет Г.К. и др. (2009). «Новые рекомендации по гемореологическим лабораторным методам» . Клиническая гемореология и микроциркуляция . 42 (2): 75–97. дои : 10.3233/CH-2009-1202 . ПМИД 19433882 . S2CID 15866651 .

[10] А. Бертон (1965). Физиология и биофизика кровообращения . Чикаго (США): Year Book Medical Publisher Inc., с. 53.

[11] Г. Терстон; Нэнси М. Хендерсон (2006). «Влияние геометрии потока на вязкоупругость крови». Биореология . 43 (6): 729–746. ПМИД 17148856 .

[12] Г. Терстон (1989). «Высвобождение плазмы - теория наслоения клеток для кровотока». Биореология . 26 (2): 199–214. дои : 10.3233/бир-1989-26208 . ПМИД 2605328 .

[13] Г. Терстон (1979). «Реологические параметры вязкости, вязкоупругости и тиксотропии крови». Биореология . 16 (3): 149–162. дои : 10.3233/бир-1979-16303 . ПМИД 508925 .

[14] Л. Пиркл и Т. Боднар, Численное моделирование кровотока с использованием обобщенной модели Олдройда-Б, Европейская конференция по вычислительной гидродинамике, 2010 г.

[Thurston-15] Jump up to: ^а ^б Терстон Г., Хендерсон Нэнси М. (2006). «Влияние геометрии потока на вязкоупругость крови». Биореология . 43 (6): 729–746. ПМИД 17148856 .

[16] Т. Как, Достижения в гемодинамике и гемореологии Том. 1, JAI Press LTD., 1996, 1-32.

[17] Р. Берд, Р. Армстронг, О. Хассагер, Динамика полимерных жидкостей; Механик жидкости, 1987, 2, 493 – 496.

[18] М. Мофрад, Х. Керхер и Р. Камм, Цитоскелетная механика: модели и измерения, 2006, 71-83.

[19] В. Лубарда и А. Марцани, Вязкоупругая реакция тонких мембран при применении. к эритроцитам, Acta Mechanica, 2009, 202, 1–16.

[20] Д. Федосов, Б. Касвелл и Г. Карниадакис, Модель крупнозернистых эритроцитов с точными механическими свойствами, реологией и динамикой, 31-я ежегодная международная конференция IEEE EMBS, Миннеаполис, Миннесота, 2009 г.

[21] Дж. Ли, З. Тан, Ю. Ся, Ю. Лу и Г. Ли, Характеристика вязкоупругих клеток с использованием фотоакустических измерений, Журнал прикладной физики, 2008, 104

[22] М. Маринкович, К. Тернер, Дж. Батлер, Дж. Фредберг и С. Суреш, Вязкоэластичность эритроцитов человека, Американский журнал физиологии. Клеточная физиология 2007, 293, 597-605.

[23] А. Юндар, В. Вон и Дж. Калхун, Влияние искусственного кровообращения и глубокой гипотермической остановки кровообращения на вязкоэластичность крови и мозговой кровоток в модели неонатального поросенка, Perfusion 2000, 15, 121–128

[24] С. Каник , Дж. Тамбака, Г. Гвидобони, А. Микелич, К. Хартли и Д. Розенштраух, Моделирование вязкоупругого поведения артериальных стенок и их взаимодействия с пульсирующим потоком крови, Журнал прикладной математики, 2006, 67, 164–193

[25] Дж. Лонг, А. Ундар, К. Мэннинг и С. Дойч, Вязкоэластичность педиатрической крови и ее значение для тестирования пульсирующего педиатрического насоса крови, Американское общество внутренних органов, 2005, 563–566.

[26] А. Ундар и В. Вон, Влияние легкого гипотермического искусственного кровообращения на вязкоэластичность крови у пациентов с аортокоронарным шунтированием, Искусственные органы 26 (11), 964–966

[27] К. Брукшир и Дж. Тарбелл, Оценка прозрачной жидкости-аналога крови: водная ксантановая камедь/глицерин, Биореология, 1993, 2, 107-16.

[28] Г. Терстон, Н. Хендерсон и М. Дженг, Влияние переливания эритроцитафереза на вязкоупругость серповидноклеточной крови, Клиническая гемореология и микроциркуляция 30 (2004) 61–75

[29] Дж. Уомерсли, Метод расчета скорости, скорости потока и вязкого сопротивления в артериях, когда известен градиент давления, Amer. Журнал Физиол. 1955, 127, 553–563.

[30] Г. Терстон, Вязкоупругость человеческой крови, Биофизический журнал, 1972, 12, 1205–1217.

[31] Г. Терстон, Вязкость и вязкоупругость крови в трубках малого диаметра, Микрососудистые исследования, 1975, 11, 133-146.

[Fung-MechProps-32] Фунг, ЮК (1993). Биомеханика: механические свойства живых тканей (2-е изд.). Нью-Йорк, штат Нью-Йорк: Спрингер. ISBN 9780387979472 .

[ 1 ]

[ 2 ]

[ 3 ]

[ 4 ]

[ 5 ]

[ 6 ]

[ 7 ]

[ 8 ]

[ 9 ]

[ 10 ]

[ 11 ]

[ 12 ]

[ 13 ]

[ 14 ]

[ 15 ]

[ 16 ]

[ 17 ]

[ 18 ]

[ 19 ]

[ 20 ]

[ 21 ]

[ 22 ]

[ 23 ]

[ 24 ]

[ 25 ]

[ 26 ]

[ 27 ]

[ 28 ]

[ 29 ]

[ 30 ]

[ 31 ]

[ 32 ]