Рэй-кастинг

Лучевое изображение идеализированного универсального шарнира с тенью

Лучевое литье является методологической основой твердотельного моделирования и рендеринга изображений в 3D CAD/CAM. По сути, это то же самое, что трассировка лучей для компьютерной графики, где виртуальные световые лучи «отбрасываются» или «отслеживаются» на пути от фокусной точки камеры через каждый пиксель в датчике камеры, чтобы определить, что видно вдоль луча в кадре. 3D сцена. Термин «Ray Casting» был введен Скоттом Ротом, когда он работал в исследовательских лабораториях General Motors в 1978–1980 годах. Его статья «Ray Casting для моделирования твердых тел». описывает смоделированные твердые объекты путем объединения примитивных твердых тел, таких как блоки и цилиндры, с использованием операторов множества объединение (+), пересечение (&) и разность (-). Общая идея использования этих бинарных операторов для твердотельного моделирования во многом принадлежит группе геометрического моделирования Фелькера и Рекичи в Рочестерском университете. См. «Твердотельное моделирование» для получения широкого обзора методов твердотельного моделирования. На этом рисунке справа показано U-образное соединение, смоделированное из цилиндров и блоков в бинарном дереве с использованием системы преобразования лучей Рота в 1979 году.

До создания лучей (и трассировки лучей) алгоритмы компьютерной графики проецировали поверхности или края (например, линии) из трехмерного мира на плоскость изображения, где нужно было применять логику видимости. Проекция плоскости мира на изображение — это трехмерное преобразование однородной системы координат (также известное как трехмерная проекция , аффинное преобразование или проективное преобразование ( гомография )). Рендеринга изображения таким способом сложно добиться, удалив скрытую поверхность/край. Кроме того, силуэты изогнутых поверхностей должны быть явно решены, поскольку это неявный побочный продукт преобразования лучей, поэтому нет необходимости явно решать их при каждом изменении вида.

Приведение лучей значительно упростило рендеринг изображений трехмерных объектов и сцен, поскольку линия преобразуется в линию. Таким образом, вместо того, чтобы проецировать изогнутые края и поверхности 3D-сцены на плоскость 2D-изображения, преобразованные линии (лучи) пересекаются с объектами на сцене. Однородное преобразование координат представляется матрицей 4х4. Математический метод является общим для компьютерной графики и геометрического моделирования. Преобразование включает в себя повороты вокруг трех осей, независимое масштабирование по осям, перемещение в 3D и даже наклон. Преобразования легко объединяются с помощью матричной арифметики. При использовании с матрицей 4x4 точка представляется как [X, Y, Z, 1], а вектор направления — как [D _x , D _y , D _z , 0]. (Четвертый термин предназначен для перевода и не применим к векторам направления.)

Концепция

Приведение лучей — самый простой из многих компьютерной графики алгоритмов рендеринга , использующих геометрический алгоритм трассировки лучей . Алгоритмы рендеринга на основе трассировки лучей работают в порядке изображения, преобразуя трехмерные сцены в двухмерные изображения. Геометрические лучи прослеживаются от глаза наблюдателя для отбора проб света ( излучения ), идущего к наблюдателю в направлении луча. Скорость и простота распределения лучей достигается за счет вычисления цвета света без рекурсивного отслеживания дополнительных лучей, которые измеряют яркость, падающую на точку попадания луча. Это исключает возможность точной визуализации отражений , преломлений или естественного затухания теней ; однако все эти элементы можно в некоторой степени подделать, творчески используя карты текстур или другие методы. Высокая скорость вычислений сделала метод raycasting удобным методом рендеринга в первых 3D-видеоиграх в реальном времени .

Идея метода луча заключается в том, чтобы проследить лучи из глаза, по одному на пиксель, и найти ближайший объект, блокирующий путь этого луча. Представьте себе изображение как дверь-ширму, где каждый квадрат на экране представляет собой пиксель. Это объект, который глаз видит через этот пиксель. Используя свойства материала и эффект освещения в сцене, этот алгоритм может определить затенение этого объекта. Делается упрощающее предположение, что если поверхность обращена к источнику света, свет достигнет этой поверхности и не будет блокироваться или находиться в тени. Затенение поверхности рассчитывается с использованием традиционных моделей затенения трехмерной компьютерной графики. Одним из важных преимуществ raycasting по сравнению со старыми алгоритмами развертки была его способность легко обрабатывать неплоские поверхности и твердые тела, такие как конусы и сферы . Если математическую поверхность можно пересечь лучом, ее можно визуализировать с помощью метода преобразования лучей. Сложные объекты можно создавать с помощью методов твердотельного моделирования и легко визуализировать.

Из аннотации к статье «Лучевое моделирование для моделирования твердых тел»: Для визуализации и анализа смоделированных составных твердых тел в качестве зондов используются виртуальные световые лучи. Благодаря своей простоте, метод ray casting надежен и расширяем. Самая сложная математическая задача — найти точки пересечения линии и поверхности. Таким образом, поверхности в виде плоскостей, квадрик, торов и, возможно, даже параметрических участков поверхности могут ограничивать примитивные твердые тела. Здесь рассматриваются адекватность и эффективность рейкастинга. Возможность быстрой генерации изображений для интерактивного моделирования является самой большой проблемой.

Camera models

Лучи света и геометрия камеры составляют основу всех геометрических рассуждений. На этом рисунке показана модель камеры-обскуры для эффекта перспективы при обработке изображений и модель параллельной камеры для массового анализа. Простая модель камеры-обскуры состоит из фокусной точки (или точки глаза) и квадратной матрицы пикселей (или экрана). Прямые лучи света проходят через матрицу пикселей, соединяя точку фокуса со сценой, по одному лучу на пиксель. Чтобы затенить изображения, интенсивность лучей измеряется и сохраняется в пикселях. Отражающая поверхность, отвечающая за значение пикселя, пересекает луч пикселя.

Когда фокусное расстояние, расстояние между фокусной точкой и экраном, бесконечно, тогда вид называется «параллельным», потому что все лучи света параллельны друг другу и перпендикулярны экрану. Хотя перспективный вид является естественным для создания изображений, в некоторых приложениях необходимы лучи, которые можно равномерно распределить в пространстве.

Для удобства моделирования типичная стандартная система координат камеры имеет экран в плоскости XY, сцену в полупространстве +Z и точку фокуса на оси -Z.

Локальная система координат камеры с «экраном» в плоскости Z=0.

Луч — это просто прямая линия в трехмерном пространстве модели камеры. Его лучше всего определить как вектор направления в параметризованной форме как точку (X ₀ , Y ₀ , Z ₀ ) и вектор направления (D _x , D _y , D _z ). В этой форме точки на линии упорядочиваются и доступны через один параметр t. Для каждого значения t определяется соответствующая точка (X, Y, Z) на линии:

X = X0 + t · Dx
Y = Y0 + t · Dy
Z = Z0 + t · Dz

Если вектор нормализован, то параметр t — это расстояние вдоль линии. Вектор можно легко нормализовать с помощью следующих вычислений:

Dist = √(Dx2 + Dy2 + Dz2)
Dx = Dx / Dist
Dy = Dy / Dist
Dz = Dz / Dist

Учитывая геометрические определения объектов, каждый из которых ограничен одной или несколькими поверхностями, результат вычисления пересечения одного луча со всеми ограниченными поверхностями на экране определяется двумя массивами:

Ray parameters:    t[1], t[2], ..., t[n]
Surface pointers:  S[1], S[2], ..., S[n]

где n — количество пересечений луча с поверхностью. Упорядоченный список параметров луча t [i] обозначает точки входа-выхода. Луч входит в тело в точке t [1], выходит в точку t [2], входит в тело в точке t [3] и т. д. Точка t [1] находится ближе всего к камере, а точка t [n] — дальше всего. В сочетании с параметрами лучей указатели поверхности содержат уникальный адрес для информации о пересекаемой поверхности. Поверхность может иметь различные свойства, такие как цвет, зеркальность, прозрачность с преломлением или без него, полупрозрачность и т. д. Твердое вещество, связанное с поверхностью, может иметь свои собственные физические свойства, такие как плотность. Это может быть полезно, например, когда объект состоит из совокупности различных материалов и интерес представляют общий центр масс и моменты инерции.

Применение информации

Три алгоритма, использующие приведение лучей, предназначены для рисования линий, создания затененных изображений и вычисления объемов и других физических свойств. Каждый алгоритм, учитывая модель камеры, излучает один луч на пиксель экрана. Для объема вычислений разрешение используемого пиксельного экрана зависит от желаемой точности решения. Для штриховых рисунков и затенения изображения разрешение определяет качество изображения.

Примеры рисунков линий, выполненных методом отбрасывания лучей. Два из них — стандартные виды в плане. На одном скрытые края показаны пунктирными линиями.

ЛИНЕЙНЫЕ ЧЕРТЕЖИ . Чтобы нарисовать видимые края твердого тела, сгенерируйте один луч на пиксель, перемещаясь сверху вниз, влево-вправо по экрану. Оцените каждый луч, чтобы идентифицировать видимую поверхность S[1], первый указатель поверхности в отсортированном списке пересечений луча и поверхности. Если видимая поверхность в месте пикселя (X, Y) отличается от видимой поверхности в пикселе (X-1, Y), отобразите вертикальную линию длиной в один пиксель с центром в точке (X-½, Y). Аналогично, если видимая поверхность в точке (X, Y) отличается от видимой поверхности в точке (X, Y-1), отобразите горизонтальную линию длиной в один пиксель с центром в точке (X, Y-½). Полученный рисунок будет состоять только из горизонтальных и вертикальных краев и будет выглядеть неровным в разрешении курса.

Система распределения лучей Рота генерировала изображения твердых объектов справа. Для оптимизации использовались коробчатые вложения, динамическое ограничение и когерентность. Для каждого изображения экран был выбран с плотностью около 100x100 (например, 10 000) лучей, и новые края были обнаружены с помощью двоичного поиска. Затем все края сопровождались отбрасыванием дополнительных лучей с шагом в один пиксель с двух сторон краев. Каждая картинка была нарисована на трубке Tektronix с разрешением 780x780.

ЗАТЕНЕННЫЕ ИЗОБРАЖЕНИЯ . Чтобы получить затененное изображение, снова наведите один луч на пиксель экрана. Однако на этот раз используйте указатель видимой поверхности S[1] в каждом пикселе, чтобы получить доступ к описанию поверхности. Исходя из этого, вычислите нормаль к поверхности в видимой точке t [1]. Значение пикселя, отображаемая интенсивность света, пропорционально косинусу угла, образованного нормалью к поверхности и вектором источника света к поверхности. Обработка всех пикселей таким образом дает изображение сцены растрового типа.

ВЫЧИСЛЕНИЕ ОБЪЕМА И МОМЕНТОВ ИНЕРЦИИ . Объем (и подобные свойства) твердого тела, ограниченного искривленными поверхностями, легко вычисляется методом интегрирования «приближающих сумм» путем аппроксимации твердого тела набором прямоугольных параллелепипедов. Это достигается путем получения «углубленного» изображения твердого тела в параллельном виде. Пропускание лучей через экран в тело разделяет тело на элементы объема. Два измерения параллелепипедов постоянны и определяются двумерным расстоянием между лучами на экране. Третье измерение является переменным и определяется вычисленной точкой входа-выхода. В частности, если горизонтальное и вертикальное расстояния между лучами на экране равны S, то объем, «обнаруженный» каждым лучом, равен

S × S ×  (t[2]-t[1]  +  t[4]-t[3]  +  ∙∙∙ + t[n]-t[n-1]) / L

где L определяется как длина вектора направления. (Если оно уже нормализовано, оно равно 1.)

L = √(Dx2 + Dy2 + Dz2)

Каждый ( t [ i ]- t [ i -1])/L представляет собой длину отрезка луча, находящегося внутри твердого тела.

На этом рисунке показаны параллелепипеды твердого тела, смоделированного с помощью метода лучевого литья. Это использование модели камеры с параллельной проекцией.

Твердое тело, моделируемое параллелепипедами

Классификация входных лучей

Рэй в бинарной твердотельной конструкции

На этом рисунке показан пример бинарных операторов в дереве композиции с использованием + и –, где оценивается один луч.

Процедура преобразования лучей начинается с вершины дерева композиции твердого тела, рекурсивно спускается вниз, классифицирует луч относительно примитивных твердых тел, а затем возвращается вверх по дереву, объединяя классификации левого и правого поддеревьев.

На этом рисунке показано объединение левой и правой классификаций для всех трех бинарных операторов.

Три бинарные операции: объединение (+), пересечение (&) и разность (-).

Реалистичные затененные изображения

Приведение лучей — это естественный инструмент моделирования для создания затененных изображений. Система преобразования лучей в оттенках серого, разработанная Скоттом Ротом и Дэниелом Бассом из GM Research Labs, создавала изображения на цветном растровом дисплее Ramtek примерно в 1979 году. Для составления изображений система предоставляла пользователю следующие элементы управления:

• Вид
  • Направление и положение просмотра
  • Фокусное расстояние: перспектива по ширине и углу до параллельности
  • Коэффициент масштабирования
• Освещение
  • Количество источников света
  • Расположение и интенсивность света
  • Опционально тень
  • Интенсивность окружающего света и фона
• Отражательная способность поверхности
  • % отражается диффузно
  • % отражено зеркально
  • % передано

Два точечных источника света создают тени.

На этом рисунке показана настольная сцена с тенями от двух точечных источников света.

Алгоритмы затенения, реализующие все реалистичные эффекты, требуют больших вычислительных затрат, но относительно просты. Например, на следующем рисунке показаны дополнительные лучи, которые могут быть отброшены от одного источника света.

Follow up rays for effects

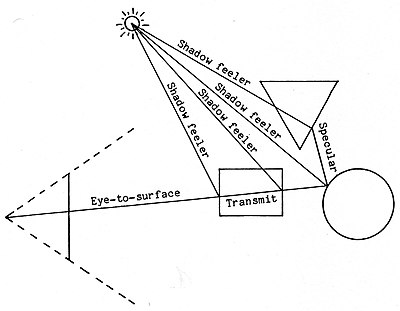
Для одного пикселя изображения, подлежащего рендерингу, алгоритм рисует луч, начинающийся с фокусной точки, и определяет, что он пересекает полупрозрачный прямоугольник и блестящий круг. Затем необходимо пропустить дополнительный луч, начиная с этой точки, в направлении, симметрично противоположном нормали к поверхности в точке пересечения луча и поверхности, чтобы определить, что видно в зеркальном отражении. Этот луч пересекает непрозрачный треугольник. Наконец, каждая точка пересечения луча и поверхности проверяется, чтобы определить, находится ли она в тени. Луч «щупа тени» направляется из точки пересечения луча и поверхности к источнику света, чтобы определить, не блокирует ли какая-либо другая поверхность этот путь.

Тернер Уиттед называет вторичные и дополнительные лучи «рекурсивной трассировкой лучей». [Рендеринг комнаты с зеркалами будет дорогостоящим, поэтому разумно ограничить количество рекурсий.] Уиттед смоделировал преломление для прозрачных пленок, создав вторичный луч из точки видимой поверхности под углом, определяемым показателем преломления твердого тела. Вторичный луч затем обрабатывается как зеркальный луч. Формулу преломления и графические примеры см. в статье Уиттеда.

Корпуса и эффективность

Приведение лучей квалифицируется как метод грубой силы для решения проблем. Минимальный алгоритм прост, особенно с учетом его многочисленных применений и простоты использования, но приложения обычно излучают много лучей. Миллионы лучей могут быть использованы для визуализации одного кадра анимационного фильма. Время компьютерной обработки увеличивается с увеличением разрешения экрана и количества примитивных тел/поверхностей в композиции.

Дерево вольеров

Благодаря использованию минимальных ограничивающих рамок вокруг тел в дереве композиции исчерпывающий поиск пересечения лучей и тел напоминает эффективный бинарный поиск. Алгоритм грубой силы выполняет исчерпывающий поиск, поскольку он всегда посещает все узлы дерева — преобразуя луч в локальные системы координат примитивов, проверяя пересечения луча с поверхностью и комбинируя классификации — даже если луч явно не попадает в твердое тело. Чтобы обнаружить «явный промах», более быстрый алгоритм использует дерево двоичной композиции как иерархическое представление пространства, которое занимает твердая композиция. Но вся информация о положении, форме и размере хранится в листьях дерева, где находятся примитивные твердые тела. Верхние и промежуточные узлы дерева определяют только операторы объединения.

Характеризация пространства, которое заполняют все твердые тела, с помощью вложений дает всем узлам дерева абстрактную сводку информации о положении и размере. Затем быстрые тесты «луч пересекает вложение» направляют поиск в иерархии. Если тест не пройден в промежуточном узле дерева, луч гарантированно классифицируется как не составной, поэтому рекурсия вниз по его поддеревьям для дальнейшего исследования не требуется.

Точно оценить экономию средств от использования вложений сложно, поскольку она зависит от пространственного распределения примитивов (распределения сложности) и организации дерева композиции. Оптимальные условия:

• Никакие примитивные ограждения не перекрываются в пространстве
• Дерево композиции сбалансировано и организовано таким образом, что субтела, расположенные рядом в пространстве, также находятся рядом в дереве.

Напротив, худшее состояние:

• Все примитивные вложения взаимно перекрываются

Ниже приведены различные улучшения производительности, сделанные в статье Рота о распределении лучей, но впоследствии были внесены значительные улучшения и другими авторами.

• Ранние выходы . Если оператор в составном узле дерева — или & и луч классифицируется как находящийся вне левого субтела составного тела, то луч будет классифицироваться как вне составного тела независимо от классификации луча по отношению к правому субтелу. твердый. Таким образом, классификация луча по правому субтелу не является необходимой, и ее следует избегать из соображений эффективности.
• Преобразования . Путем первоначального объединения преобразования экрана в сцену с преобразованием сцены в локальную примитива и сохранения результирующих преобразований экрана в локальную структуру в структурах данных примитива можно исключить одно лучевое преобразование на каждое пересечение луча и поверхности.
• Рекурсия . Учитывая глубокое дерево композиции, рекурсия может быть дорогостоящей в сочетании с выделением и освобождением памяти. Рекурсию можно моделировать, используя статические массивы в виде стеков.
• Динамическое ограничение . Если должны отображаться только видимые края твердого тела, алгоритм преобразования лучей может динамически связывать луч, чтобы пресечь поиск. То есть, обнаружив, что луч пересекает субтело, алгоритм может использовать точку пересечения, ближайшую к экрану, чтобы ужесточить границу глубины для теста «поле пересечений лучей». Это работает только для + части дерева, начиная сверху. С – и & близлежащие «внутренние» части луча позже могут стать «внешними».
• Согласованность . Принцип когерентности заключается в том, что поверхности, видимые в двух соседних пикселях, скорее всего, будут одинаковыми, а не разными. Разработчики компьютерной графики и систем машинного зрения применили эту эмпирическую истину для повышения эффективности и производительности. Для линейных рисунков область изображения, содержащая края, обычно намного меньше общей площади изображения, поэтому распределение лучей должно быть сосредоточено вокруг краев, а не в открытых областях. Это можно эффективно реализовать, разрежая выборку экрана лучами, а затем определяя края, когда соседние лучи идентифицируют разные видимые поверхности, с помощью двоичного поиска.

Сглаживание

Неровные края, вызванные сглаживанием, являются нежелательным эффектом методов выборки точек и являются классической проблемой алгоритмов растрового отображения. Линейные или плавно изогнутые края будут выглядеть неровными и особенно нежелательны в анимации, поскольку при движении изображения края кажутся размытыми или похожими на маленькие движущиеся эскалаторы. Кроме того, могут быть потеряны детали сцены, меньшие, чем расстояние между лучами. Неровные края линейного рисунка можно сгладить, следуя за краем. Цель такого алгоритма — минимизировать количество строк, необходимых для рисования изображения, с точностью до одного пикселя. В результате края становятся гладкими. Линейные рисунки выше были нарисованы таким образом.

Чтобы сгладить неровные края затененного изображения с точностью до субпикселя, необходимо отбросить дополнительные лучи для получения информации о краях. (Общий подход см . в разделе «Суперсэмплинг» .) Края образуются в результате пересечения поверхностей или профиля изогнутой поверхности. Применяя «когерентность», как описано выше, посредством двоичного поиска, если видимая поверхность в пикселе (X,Y) отличается от видимой поверхности в пикселе (X+1,Y), то луч может быть сгенерирован посередине их в (X+ ½,Y) и видимая поверхность там идентифицирована. Расстояние между точками выборки может быть дополнительно разделено, но поиск не обязательно должен быть глубоким. Основная глубина поиска для сглаживания неровных краев является функцией градиента интенсивности по краю. Поскольку (1) область изображения, содержащая края, обычно составляет небольшой процент от общей площади и (2) дополнительные лучи, отбрасываемые при бинарном поиске, могут быть ограничены по глубине (глубина видимых примитивов, образующих края), стоимость сглаживание неровных краев доступно по цене.

История лучевого кастинга

Историю создания лучей см. в разделе «Трассировка лучей (графика)», поскольку обе они, по сути, представляют собой одну и ту же технику под разными названиями. Скотт Рот изобрел термин «кастинг лучей» еще до того, как услышал о «трассировке лучей». Кроме того, разработка Скоттом Ротом метода распределения лучей в GM Research Labs происходила одновременно с работой Тернера Уиттеда по трассировке лучей в Bell Labs.

Приведение лучей в ранних компьютерных играх

Игра использует рендеринг ray casting, используя передовые методы для рендеринга пола на нескольких уровнях высоты.

В ранних играх от первого лица рейкастинг использовался для эффективной визуализации трехмерного мира из двухмерного игрового поля с использованием простого одномерного сканирования по горизонтальной ширине экрана. Ранние шутеры от первого лица использовали 2D-рейтинг как метод создания 3D-эффекта из 2D-мира. Хотя мир выглядит трехмерным, игрок не может смотреть вверх или вниз или только под ограниченными углами с сдвиговым искажением. Этот стиль рендеринга устраняет необходимость запускать луч для каждого пикселя кадра, как в случае с современными движками; как только точка попадания найдена, к текстуре поверхности применяется проекционное искажение, и из результата в кадр копируется весь вертикальный столбец. Этот стиль рендеринга также накладывает ограничения на тип рендеринга, который может быть выполнен, например, сортировка по глубине , но буферизация глубины не . То есть полигоны должны быть сплошными друг перед другом или позади друг друга, они не могут частично перекрываться или пересекаться.

Вольфенштейн 3D

Видеоигра Wolfenstein 3D была построена на основе квадратной сетки стен одинаковой высоты, сочетающихся с однотонными полами и потолками. Чтобы нарисовать мир, для каждого столбца пикселей экрана трассировался один луч , а вертикальный фрагмент текстуры стены выбирался и масштабировался в зависимости от того, где в мире луч достигает стены и как далеко он проходит перед этим.

Уровни на основе сетки преследовали двойную цель: столкновения со стенками лучей можно обнаружить быстрее, поскольку потенциальные попадания становятся более предсказуемыми, а затраты памяти уменьшаются. Однако кодирование открытых пространств требует дополнительного места.

Заклинатель теней

В от Raven Software игре ShadowCaster используется улучшенный движок на основе Wolfenstein с добавленными текстурами полов и потолков и переменной высотой стен.

команчей Серия

Движок Voxel Space , разработанный NovaLogic для Comanche игр , прослеживал луч через каждый столбец пикселей экрана и сравнивал каждый луч с точками на карте высот . Затем он преобразовывал каждый элемент карты высот в столбец пикселей, определял, какие из них видимы (то есть не перекрыты пикселями, нарисованными спереди), и рисовал их соответствующим цветом из карты текстуры.

За пределами рейкастинга

Более поздние для DOS игры , такие как DOOM от id Software, сохранили многие ограничения скорости 2.5D для raycasting, но перешли на альтернативные методы рендеринга (например, BSP ), что лишило их движков raycasting.

Настройка вычислительной геометрии

В вычислительной геометрии проблема распределения лучей также известна как проблема стрельбы лучами и может быть сформулирована как следующая задача запроса: задан набор объектов в d -мерном пространстве, предварительно обработайте их в структуру данных так, чтобы для каждого луча запроса первоначальный объект, на который попал луч, можно быстро найти. Проблема исследовалась для различных настроек: размерность пространства, типы объектов, ограничения на лучи запроса и т.д. Один из методов — использование разреженного октодерева вокселей .

См. также

• Трассировка лучей (графика). Более сложный алгоритм преобразования лучей, учитывающий глобальное освещение.
• Фотонное картирование
• Радиосити (компьютерная графика)
• Отслеживание пути
• Объемный луч
• 2.5D

Внешние ссылки

• Пример рейкастинга в браузере. (недоступно)
• Плоскости Raycasting в WebGL с исходным кодом
• Интерактивный рейкастер для Commodore 64 размером 254 байта (с исходным кодом)
• Интерактивный рейкастер для MSDOS размером 64 байта (с исходным кодом)