Изометрическая графика видеоигр

Изометрическая графика видеоигр — это графика, используемая в видеоиграх и пиксельной графике , в которой используется параллельная проекция , но которая наклоняет точку обзора , чтобы раскрыть грани окружающей среды, которые в противном случае не были бы видны с точки зрения сверху вниз или вида сбоку , создавая тем самым трехмерное изображение . -мерный (3D) эффект . Несмотря на название, изометрическая компьютерная графика не обязательно является истинно изометрической — т. е. $оси x$ , $y$ и $z$ не обязательно ориентированы под углом 120° друг к другу. Вместо этого используются различные углы, диметрическая проекция наиболее распространенными из которых являются и соотношение пикселей 2:1. Термины «перспектива 3/4», «вид 3/4», « 2,5D » и «псевдо3D» также иногда используются, хотя в других контекстах эти термины могут иметь несколько иное значение.

Когда-то изометрическая проекция стала менее распространенной с появлением более мощных систем трехмерной графики , а также по мере того, как видеоигры стали больше фокусироваться на действиях и отдельных персонажах. ^[1] Однако видеоигры, использующие изометрическую проекцию, особенно компьютерные ролевые игры , в последние годы возродились на инди-игровой сцене. ^[1]^[2]

Обзор [ править ]

Преимущества [ править ]

Соответствующие углы поворота 3D-камеры для истинной изометрической проекции (слева) и формы диметрической проекции, обычно встречающейся в видеоиграх и пиксельной графике (справа). ^[3] Выражение

arctan(sin(45°))

равно ≈35,264°.

Настоящий изометрический рисунок куба. Обратите внимание на углы в 120°, разделяющие оси x , y и z , а также на равные длины каждого из ребер куба. Выражение

arctan(sin(\approx35,264°))

или

arctan(sin(arctan(sin(45°))))

равно 30° и формирует соотношение пикселей ≈1,732:1.

Форма диметрической проекции, обычно используемая в видеоиграх и пиксельной графике. Только два угла, разделяющие оси x , y и z, одинаковы, и только некоторые длины ребер куба равны. Выражение

arctan(sin(30°))

равно ≈26,565° и формирует соотношение пикселей 2:1.

Хорошо реализованная изометрическая система никогда не должна заставлять игрока думать о камере. Вы должны иметь возможность быстро и интуитивно перемещать взгляд на то, на что вам нужно смотреть, и никогда не учитывать механику камеры. Попытка использовать полноценную 3D-камеру во время тактического сражения в реальном времени наверняка вызовет возгорание шлема у новых игроков, поскольку они быстро перегружены механикой.

Трент Остер, соучредитель BioWare и основатель Beamdog ^[1]

В области компьютерных, видеоигр и пиксельной графики этот метод стал популярным из-за простоты, с которой 2D - спрайтовую и тайловую можно создать графику для представления 3D- игровой среды. Поскольку параллельно проецируемые объекты не изменяются в размере при перемещении по области, компьютеру не требуется масштабировать спрайты или выполнять сложные вычисления, необходимые для имитации визуальной перспективы . Это позволило 8-битным и 16-битным игровым системам (а в последнее время и портативным и мобильным системам) быстро и легко отображать большие игровые области. И хотя проблемы с путаницей глубины при параллельном проецировании иногда могут быть проблемой, хорошая игра и дизайн уровней могут облегчить эту проблему.

Кроме того, хотя это и не ограничивается строго изометрической графикой видеоигр, предварительно визуализированная 2D-графика может обладать более высокой точностью и использовать более совершенные графические методы, чем это возможно на общедоступном компьютерном оборудовании, даже с аппаратным 3D-ускорением . ^[4] Подобно современной компьютерной графике , используемой в кино , графика может быть визуализирована один раз на мощном суперкомпьютере или ферме рендеринга , а затем многократно отображена на менее мощном потребительском оборудовании, например, на телевизорах , планшетных компьютерах и смартфонах . Это означает, что статическая предварительно отрисованная изометрическая графика часто выглядит лучше по сравнению с ее современными аналогами, визуализируемыми в реальном времени, и может со временем стареть лучше по сравнению с аналогами. ^[2] Однако сегодня это преимущество может быть менее выраженным, чем в прошлом, поскольку развитие графических технологий уравнивает или приводит к уменьшению отдачи , а нынешний уровень графической точности становится «достаточно хорошим» для многих людей. ^{[ нужна ссылка ]}

Наконец, использование изометрической или почти изометрической перспективы в видеоиграх также дает игровые преимущества. Например, по сравнению с игрой с видом сверху , они добавляют третье измерение, открывая новые возможности для прицеливания и платформера . ^[1] Во-вторых, по сравнению с видеоиграми от первого или третьего лица , они позволяют вам легче выставлять на поле и управлять большим количеством юнитов, например, полной группой персонажей в компьютерной ролевой игре или армией миньонов в стратегическая игра в реальном времени . ^[1] игры Кроме того, они могут облегчить ситуации, когда игрок может отвлечься от основной механики из-за необходимости постоянно управлять громоздкой 3D-камерой. ^[1] Т.е. игрок может сосредоточиться на самой игре, а не на манипулировании игровой камерой. ^[1]

В наши дни возрождение изометрической проекции является не просто источником ностальгии, а результатом реальных, ощутимых преимуществ дизайна. ^[1]

Недостатки [ править ]

Некоторые недостатки предварительно визуализированной изометрической графики заключаются в том, что по мере того, как разрешения дисплея и соотношения сторон дисплея продолжают меняться, статические 2D-изображения необходимо каждый раз перерисовывать, чтобы идти в ногу со временем, иначе они могут пострадать от эффектов пикселизации и потребовать анти- -алиасинг . Однако повторный рендеринг игровой графики не всегда возможен; как это было в 2012 году, когда Beamdog переделала (1998) от BioWare Baldur's Gate . В Beamdog не хватало творческих ресурсов исходных разработчиков (исходные данные были потеряны в результате наводнения). ^[5]) и выбрал простое масштабирование 2D-графики со «сглаживанием» без повторного рендеринга спрайтов игры. Результатом стала определенная «размытость» или отсутствие «четкости» по сравнению с графикой оригинальной игры. ^{[ нужна ссылка ]} Однако это не влияет на полигональные изометрические видеоигры, отображаемые в реальном времени, поскольку изменение их разрешения экрана или соотношения сторон по сравнению с этим тривиально.

от «настоящей» проекции Отличия изометрической

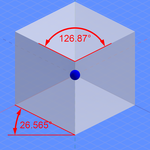
Проекция, обычно используемая в видеоиграх, немного отличается от «истинной» изометрии из-за ограничений растровой графики . Линии в $направлениях x$ и $y$ не будут следовать аккуратному рисунку пикселей, если нарисованы под необходимым углом 30° к горизонтали. Хотя современные компьютеры могут устранить эту проблему с помощью сглаживания , более ранняя компьютерная графика не поддерживала достаточное количество цветов и не обладала достаточной мощностью процессора для этого. будет использоваться соотношение шаблонов пикселей 2:1 $Вместо этого для рисования линий осей x$ и $y$ , в результате чего эти оси будут следовать под углом ≈26,565° ( $arctan(1/2)$ ) к горизонтали. (Однако игровые системы, в которых не используются квадратные пиксели , могут выдавать разные углы, включая «истинную» изометрию.) Следовательно, эту форму проекции точнее описать как вариант диметрической проекции , поскольку только два из трех углов между оси равны между собой, т.е. $(\approx116,565°, \approx116,565°, \approx126,870°)$ .

История изометрических видеоигр [ править ]

Некоторые трехмерные игры были выпущены еще в 1970-х годах, но первыми видеоиграми, в которых использовался особый визуальный стиль изометрической проекции в описанном выше значении, были аркадные игры начала 1980-х годов.

1980-е годы [ править ]

Использование изометрической графики в видеоиграх началось с Data East от DECO Cassette System аркадной игры Treasure Island . ^[6] выпущен в Японии в сентябре 1981 года, ^[7] но он не был выпущен на международном уровне до июня 1982 года. ^[8] Первой изометрической игрой, выпущенной на международном уровне, была Sega от Zaxxon , которая была значительно более популярной и влиятельной; ^[9]^[10] он был выпущен в Японии в декабре 1981 года. ^[11] и на международном уровне в апреле 1982 года. ^[8] Zaxxon — изометрический шутер , в котором игрок управляет космическим самолетом и проходит уровни с прокруткой . Это также одна из первых видеоигр, в которых отображаются тени. ^[9]

Еще одна ранняя изометрическая игра — Q*bert . ^[12] Уоррен Дэвис и Джефф Ли начали программировать концепцию примерно в апреле 1982 года. Производство игры началось летом, а затем было выпущено в октябре или ноябре 1982 года. ^[13] Q*bert показывает статическую пирамиду в изометрической перспективе, где игрок управляет персонажем, который может прыгать по пирамиде. ^[9]

В феврале 1983 года ^[8] Была выпущена изометрическая аркадная платформерная игра Congo Bongo , работающая на том же оборудовании, что и Zaxxon . ^[14] Это позволяет персонажу игрока перемещаться по изометрическим уровням без прокрутки, включая трехмерное восхождение и падение. То же самое возможно и в аркадной игре Marble Madness , вышедшей в 1984 году.

2D (слева) и 3D (справа) координаты типичного диметрического спрайта видеоигры.

В 1983 году изометрические игры больше не были эксклюзивом для рынка аркад и также проникли на домашние компьютеры с выпуском Blue Max для 8-битных компьютеров Atari и Ant Attack для ZX Spectrum . В Ant Attack игрок может двигаться вперед в любом направлении прокрутки игры, предлагая полное свободное движение, а не фиксированное на одной оси, как в Zaxxon . Виды также можно изменить вокруг оси 90 градусов . ^[15] Журнал ZX Spectrum Crash присвоил ему 100% награду в категории графики за эту новую технику, известную как «Soft Solid 3-D». ^[16]

Годом позже игра Knight Lore вышла для ZX Spectrum. Обычно это считалось революционным титулом. ^[17] что определило последующий жанр изометрических приключенческих игр. ^[18] После Knight Lore на домашних компьютерах появилось множество изометрических игр — до такой степени, что когда-то она считалась второй по популярности частью программного обеспечения после WordStar , по словам исследователя Яна Крикке. ^[19] Другими примерами из них были «Встреча на шоссе» (1985), «Бэтмен» (1986), «По уши» (1987). ^[20] и Ла Абадия дель Кримен (1987). Однако изометрическая перспектива не ограничивалась аркадными/приключенческими играми; например, в стратегической игре Populous 1989 года использовалась изометрическая перспектива.

1990-е годы [ править ]

Телевизор, нарисованный в почти изометрической пиксельной графике 2:1 (увеличен, чтобы показать структуру пикселей) ^[21]

3D-рендеринг, в видеоигре Fallout . имитирующий использование триметрической проекции и шестиугольной сетки

На протяжении 1990-х годов в нескольких успешных играх, таких как Syndicate (1993), SimCity 2000 (1994), Civilization II (1996), X-COM (1994) и Diablo (1996), использовалась фиксированная изометрическая перспектива. Но с появлением 3D-ускорения на персональных компьютерах и игровых консолях игры, ранее использовавшие 2D-перспективу, обычно вместо этого начали переключаться на истинное 3D (и перспективную проекцию ). Это можно увидеть в преемниках вышеупомянутых игр: например, SimCity (2013), Civilization VI (2016), XCOM: Enemy Unknown (2012) и Diablo III (2012) используют трехмерную полигональную графику; и хотя в Diablo II (2000) использовалась 2D-перспектива с фиксированной перспективой, как и в его предшественнике, она опционально допускала перспективное масштабирование спрайтов на расстоянии, чтобы придать им «псевдо-3D» вид. ^[22]

Также в 1990-х годах изометрическая графика начала использоваться в японских ролевых видеоиграх (JRPG) для консольных систем , особенно в тактических ролевых играх , многие из которых до сих пор используют изометрическую графику. Примеры включают Front Mission (1995), Tactics Ogre (1995) и Final Fantasy Tactics (1997), последняя из которых использовала 3D-графику для создания среды, в которой игрок мог свободно вращать камеру. Другие игры, такие как Vandal Hearts (1996) и Breath of Fire III (1997), тщательно имитировали изометрический или параллельный вид, но на самом деле использовали перспективную проекцию.

Изометрические или подобные им перспективы становятся популярными в ролевых видеоиграх , таких как Fallout и Baldur’s Gate . В некоторых случаях эти ролевые игры стали определяться их изометрической перспективой, которая позволяет вести более масштабные сражения. ^[1]

2010-е [ править ]

Изометрическая проекция продолжает оставаться актуальной в новом тысячелетии после выпуска финансируемых краудфандингом нескольких новых ролевых игр, на Kickstarter . ^[1] К ним относятся серия Shadowrun Returns (2013-2015) от Harebrained Schemes ; сериалы Pillars of Eternity (2015–2018) и Tyranny (2016) от Obsidian Entertainment ; и Torment: Tides of Numenera (2017) от inXile Entertainment . ^{[ нужна ссылка ]} И Obsidian Entertainment, и inXile Entertainment наняли или были основаны бывшими членами Black Isle Studios и Interplay Entertainment. Obsidian Entertainment, в частности, хотела «вернуть внешний вид игр на Infinity Engine, таких как Baldur's Gate , Icewind Dale и Planescape: Torment ». ^[1] Наконец, несколько псевдоизометрических 3D-ролевых игр, таких как Divinity: Original Sin (2014), Wasteland 2 (2014) и Dead State (2014), были профинансированы с помощью Kickstarter. Однако эти игры отличаются от вышеупомянутых игр тем, что в них используется перспективная проекция вместо параллельной проекции . ^{[ нужна ссылка ]}

Использование связанных прогнозов и методов [ править ]

Термин «изометрическая перспектива» часто неправильно применяется к любой игре с видом сверху — обычно с фиксированным углом, который на первый взгляд кажется «изометрическим». К ним относятся вышеупомянутые с диметрической проекцией видеоигры ; игры, использующие триметрическую проекцию , такие как Fallout (1997) ^[23] и SimCity 4 (2003 г.); ^[24] игры, использующие косую проекцию , такие как Ultima Online (1997) ^[25] и Божественная Божественность (2002); ^[26] и игры, в которых используется комбинация перспективной проекции и вида с высоты птичьего полета , такие как Silent Storm (2003), ^[27] Свет факела (2009) ^[28] и Божественность: Первородный грех (2014). ^[29]

Кроме того, не все «изометрические» видеоигры полагаются исключительно на предварительно отрендеренные 2D-спрайты. Есть, например, игры, которые полностью используют полигональную 3D-графику, но визуализируют свою графику с использованием параллельной проекции вместо перспективной, такие как Syndicate Wars (1996), Dungeon Keeper (1997) и Depths of Peril (2007); игры, в которых используется комбинация предварительно обработанных 2D-фонов и 3D-моделей персонажей, визуализированных в реальном времени, такие как The Temple of Elemental Evil (2003) и Torment: Tides of Numenera (2017); и игры, в которых трехмерный фон, визуализируемый в реальном времени, сочетается с нарисованными от руки двухмерными спрайтами персонажей, такие как Final Fantasy Tactics (1997) и Disgaea: Hour of Darkness (2003).

сверху вниз Одним из преимуществ наклонной проекции по сравнению с другими почти изометрическими перспективами является то, что объекты более плотно прилегают к неперекрывающимся квадратным графическим элементам, тем самым потенциально устраняя необходимость в дополнительном Z-порядке в вычислениях и требуя меньше пикселей.

Сопоставление экрана с мировыми координатами [ править ]

Одной из наиболее распространенных проблем при программировании игр, в которых используются изометрические (или, скорее, диметрические) проекции, является способность сопоставлять события, происходящие на 2D-плоскости экрана, и фактическое местоположение в изометрическом пространстве, называемом мировым пространством. Типичным примером является выбор плитки, которая находится прямо под курсором, когда пользователь щелкает мышью. Один из таких методов заключается в использовании тех же матриц вращения , которые изначально создавали изометрический вид в обратном порядке, чтобы превратить точку в экранных координатах в точку, которая лежала бы на поверхности игрового поля до ее поворота. Затем мировые значения x и y можно рассчитать путем деления на ширину и высоту плитки.

Другой способ, который требует меньше вычислительных затрат и может дать хорошие результаты, если метод вызывается для каждого кадра, основан на предположении, что квадратная доска была повернута на 45 градусов, а затем сжалась до половины своей первоначальной высоты. Виртуальная сетка накладывается на проекцию, как показано на схеме, с осями virtual-x и virtual-y. Нажатие на любую плитку на центральной оси доски, где (x, y) = (tileMapWidth / 2, y), приведет к созданию одинакового значения плитки как для world-x, так и для world-y, которое в этом примере равно 3 (индексировано 0). . Выбор плитки, лежащей на одну позицию справа в виртуальной сетке, фактически перемещает на одну плитку меньше в мире-y и на одну плитку больше в мире-x. Это формула, которая вычисляет мир-x, беря виртуальный-y и добавляя виртуальный-x из центра доски. Аналогично, world-y рассчитывается путем взятия виртуального-y и вычитания виртуального-x. Эти расчеты производятся от центральной оси, как показано на рисунке, поэтому результаты необходимо перевести на половину доски. Например, на языке программирования C:

float virtualTileX = screenx / virtualTileWidth;
float virtualTileY = screeny / virtualTileHeight;

// some display systems have their origin at the bottom left while the tile map at the top left, so we need to reverse y
float inverseTileY = numberOfTilesInY - virtualTileY;

float isoTileX = inverseTileY + (virtualTileX - numberOfTilesInX / 2);
float isoTileY = inverseTileY - (virtualTileX - numberOfTilesInY / 2);

На первый взгляд этот метод может показаться нелогичным, поскольку берутся координаты виртуальной сетки, а не исходного изометрического мира, и между виртуальными плитками и изометрическими плитками нет однозначного соответствия. Плитка в сетке будет содержать более одной изометрической плитки, и в зависимости от того, где на нее щелкнут, она должна отображаться в разных координатах. Ключевым моментом этого метода является то, что виртуальные координаты представляют собой числа с плавающей запятой, а не целые числа. Значение виртуальных x и y может быть (3,5, 3,5), что означает центр третьей плитки. На диаграмме слева это подробно показано на третьей плитке по оси y. Когда виртуальные x и y должны в сумме составлять 4, мир x также будет равен 4.

Примеры [ править ]

См. также [ править ]

Обрезка
Двигатель киносъемки
Категория:Видеоигры с изометрической графикой : список изометрических видеоигр
Категория:Видеоигры с наклонной графикой : список видеоигр с наклонной графикой
Commons:Категория:Изометрические скриншоты видеоигр : галерея изометрических скриншотов видеоигр

Ссылки [ править ]

↑ Перейти обратно: Перейти обратно: ^а ^б ^с ^д ^и ^ж ^г ^час ^я ^дж ^к Синьор, Джереми (19 декабря 2014 г.). «Ретронавты: сохраняющаяся актуальность изометрических игр» . usgamer.net . Геймерская сеть. Архивировано из оригинала 9 августа 2015 г. Проверено 1 апреля 2017 г.
↑ Перейти обратно: Перейти обратно: ^а ^б Вас, Герго (18 марта 2013 г.). «Самые красивые изометрические игры» . котаку.com . Медиагруппа Гизмодо . Проверено 1 апреля 2017 г.
^ Примечание: синие векторы указывают на положение камеры. Красные дуги обозначают вращение вокруг горизонтальной и вертикальной осей. Белые поля соответствуют тем, что показаны на изображениях вверху статьи. Обратите внимание, как на левом изображении вектор камеры проходит через две противоположные вершины куба.
^ Вас, Герго (10 мая 2013 г.). «Видеоигры с самым запоминающимся предварительно отрендеренным фоном» . Котаку.com . Медиагруппа Гизмодо . Проверено 1 апреля 2017 г.
^ Грейсон, Натан (01 апреля 2016 г.). «Борьба за возвращение Baldur’s Gate спустя 17 лет» . Котаку.com . Медиагруппа Гизмодо . Проверено 11 апреля 2017 г. Это была большая проблема, потому что все оригинальные ресурсы Baldur’s Gate, такие как 3D-модели, из которых состоят эти спрайты, 3D-модели уровней оригинальной игры и эти архивы, были утеряны.
^ Остров сокровищ в списке убийц видеоигр
^ «Остров сокровищ (регистрационный номер PA0000187784)» . Бюро авторских прав США . Проверено 5 мая 2021 г.
↑ Перейти обратно: Перейти обратно: ^а ^б ^с Акаги, Масуми (13 октября 2006 г.). телеигр Список аркадных : внутреннее • зарубежное издание (1971–2005 гг .) (на японском языке: Агентство новостей развлечений, стр. 35, 115, 131. ISBN) . 978-4990251215 .
↑ Перейти обратно: Перейти обратно: ^а ^б ^с Перрон, Бернар; Вольф, Марк Дж. П. (12 ноября 2008 г.). Читатель теории видеоигр 2 . Тейлор и Фрэнсис. п. 158. ИСБН 978-0-415-96282-7 . Проверено 13 ноября 2022 г.
^ Zaxxon в убийственном списке видеоигр
^ «Zaxxon (регистрационный номер PA0000135301)» . Бюро авторских прав США . Проверено 5 мая 2021 г.
^ Q*bert в убийственном списке видеоигр
^ Дэвис, Уоррен . «Создание Q*Bert» . Coinop.org . Проверено 26 сентября 2011 г.
^ Конго Бонго в убийственном списке видеоигр
^ «Придайте новую форму спектрумовским играм» . Пользователь Синклера (21). Декабрь 1983 года . Проверено 2 марта 2009 г.
^ «Мягкая твердая 3D атака муравьев» . АВАРИЯ (1). Февраль 1984 года . Проверено 29 сентября 2008 г.
^ «Идеальная игра в игру - обзор компании». Ретро-микроигры Action – Лучшие игрыTM Retro Volume 1 . Хайбери Развлечения. 2006. с. 25.
^ Стивен Коллинз. «Игровая графика в эпоху 8-битных компьютеров» . Информационные бюллетени по компьютерной графике . СИГГРАФ. Архивировано из оригинала 9 сентября 2012 г. Проверено 16 августа 2007 г.
^ Крикке, Дж. (июль – август 2000 г.). «Аксонометрия: вопрос перспективы». IEEE Компьютерная графика и приложения . 20 (4): 7–11. дои : 10.1109/38.851742 . « Говорят, что Knight Lore является второй по количеству клонов программой после программы обработки текста Word Star ».
^ «В поисках старого ракурса» . АВАРИЯ (51). Апрель 1988 года . Проверено 29 сентября 2008 г.
^ Примечание. Шаблон пикселей 2:1 на почти изометрическом изображении обеспечивает более плавные линии, чем на изометрическом.
^ «Diablo II близок к завершению, поскольку Blizzard готовится к заключительной фазе бета-тестирования» . Найти статьи . Деловая сеть БНЕТ . Маркетвайр . Май 2000 г. Архивировано из оригинала 10 июля 2012 г. Проверено 29 сентября 2008 г.
^ Грин, Джефф (29 февраля 2000 г.). «Предварительный просмотр GameSpot: Arcanum» . ГеймСпот . CNET Networks, Inc. Проверено 10 января 2008 г.
^ Баттс, Стив (9 сентября 2003 г.). «SimCity 4: Обзор часа пик» . ИГН ПК . ИГН Энтертейнмент, Инк . Архивировано из оригинала 20 сентября 2003 года . Проверено 10 января 2008 г.
^ Грили, Дэйв; Бен Сойер (19 августа 1997 г.). «Создала ли Origin первый настоящий мир онлайн-игр?» . Гамасутра . ООО «СМП Медиа» . Проверено 17 декабря 2007 г.
^ Уокер, Трей (12 июля 2002 г.). «Divine Divinity становится золотом» . ГеймСпот . CBS Интерактив . Проверено 11 апреля 2017 г.
^ О'Хаган, Стив (7 августа 2008 г.). «Превью ПК: Silent Storm» . ComputerAndVideoGames.com . Фьючер Паблишинг Лимитед . Проверено 13 декабря 2007 г.
^ Макдугалл, Джаз (4 ноября 2009 г.). «Обзор Факела» . Игровой радар . Проверено 6 ноября 2009 г.
^ Гамильтон, Кирк (3 июля 2014 г.). «Я рад, что они все еще делают такие игры, как Divinity: Original Sin» . Котаку . Медиагруппа Гизмодо . Проверено 11 апреля 2017 г.

Внешние ссылки [ править ]

Классические 8-битные изометрические игры, пытавшиеся сломать стереотипы на Eurogamer.com.
Самые красивые изометрические игры на Kotaku.com
Лучшие изометрические видеоигры на Kotaku.com

[usgamer-1] Перейти обратно: Перейти обратно: ^а ^б ^с ^д ^и ^ж ^г ^час ^я ^дж ^к Синьор, Джереми (19 декабря 2014 г.). «Ретронавты: сохраняющаяся актуальность изометрических игр» . usgamer.net . Геймерская сеть. Архивировано из оригинала 9 августа 2015 г. Проверено 1 апреля 2017 г.

[bestlooking-2] Перейти обратно: Перейти обратно: ^а ^б Вас, Герго (18 марта 2013 г.). «Самые красивые изометрические игры» . котаку.com . Медиагруппа Гизмодо . Проверено 1 апреля 2017 г.

[3] Примечание: синие векторы указывают на положение камеры. Красные дуги обозначают вращение вокруг горизонтальной и вертикальной осей. Белые поля соответствуют тем, что показаны на изображениях вверху статьи. Обратите внимание, как на левом изображении вектор камеры проходит через две противоположные вершины куба.

[prerend-4] Вас, Герго (10 мая 2013 г.). «Видеоигры с самым запоминающимся предварительно отрендеренным фоном» . Котаку.com . Медиагруппа Гизмодо . Проверено 1 апреля 2017 г.

[kotakusprites-5] Грейсон, Натан (01 апреля 2016 г.). «Борьба за возвращение Baldur’s Gate спустя 17 лет» . Котаку.com . Медиагруппа Гизмодо . Проверено 11 апреля 2017 г. Это была большая проблема, потому что все оригинальные ресурсы Baldur’s Gate, такие как 3D-модели, из которых состоят эти спрайты, 3D-модели уровней оригинальной игры и эти архивы, были утеряны.

[6] Остров сокровищ в списке убийц видеоигр

[7] «Остров сокровищ (регистрационный номер PA0000187784)» . Бюро авторских прав США . Проверено 5 мая 2021 г.

[Akagi-8] Перейти обратно: Перейти обратно: ^а ^б ^с Акаги, Масуми (13 октября 2006 г.). телеигр Список аркадных : внутреннее • зарубежное издание (1971–2005 гг .) (на японском языке: Агентство новостей развлечений, стр. 35, 115, 131. ISBN) . 978-4990251215 .

[Perron-9] Перейти обратно: Перейти обратно: ^а ^б ^с Перрон, Бернар; Вольф, Марк Дж. П. (12 ноября 2008 г.). Читатель теории видеоигр 2 . Тейлор и Фрэнсис. п. 158. ИСБН 978-0-415-96282-7 . Проверено 13 ноября 2022 г.

[10] Zaxxon в убийственном списке видеоигр

[US-11] «Zaxxon (регистрационный номер PA0000135301)» . Бюро авторских прав США . Проверено 5 мая 2021 г.

[12] Q*bert в убийственном списке видеоигр

[13] Дэвис, Уоррен . «Создание Q*Bert» . Coinop.org . Проверено 26 сентября 2011 г.

[14] Конго Бонго в убийственном списке видеоигр

[15] «Придайте новую форму спектрумовским играм» . Пользователь Синклера (21). Декабрь 1983 года . Проверено 2 марта 2009 г.

[16] «Мягкая твердая 3D атака муравьев» . АВАРИЯ (1). Февраль 1984 года . Проверено 29 сентября 2008 г.

[GamesTM-17] «Идеальная игра в игру - обзор компании». Ретро-микроигры Action – Лучшие игрыTM Retro Volume 1 . Хайбери Развлечения. 2006. с. 25.

[SIGGRAPH-18] Стивен Коллинз. «Игровая графика в эпоху 8-битных компьютеров» . Информационные бюллетени по компьютерной графике . СИГГРАФ. Архивировано из оригинала 9 сентября 2012 г. Проверено 16 августа 2007 г.

[19] Крикке, Дж. (июль – август 2000 г.). «Аксонометрия: вопрос перспективы». IEEE Компьютерная графика и приложения . 20 (4): 7–11. дои : 10.1109/38.851742 . « Говорят, что Knight Lore является второй по количеству клонов программой после программы обработки текста Word Star ».

[20] «В поисках старого ракурса» . АВАРИЯ (51). Апрель 1988 года . Проверено 29 сентября 2008 г.

[21] Примечание. Шаблон пикселей 2:1 на почти изометрическом изображении обеспечивает более плавные линии, чем на изометрическом.

[22] «Diablo II близок к завершению, поскольку Blizzard готовится к заключительной фазе бета-тестирования» . Найти статьи . Деловая сеть БНЕТ . Маркетвайр . Май 2000 г. Архивировано из оригинала 10 июля 2012 г. Проверено 29 сентября 2008 г.

[gspot_fo-23] Грин, Джефф (29 февраля 2000 г.). «Предварительный просмотр GameSpot: Arcanum» . ГеймСпот . CNET Networks, Inc. Проверено 10 января 2008 г.

[ign_sc4-24] Баттс, Стив (9 сентября 2003 г.). «SimCity 4: Обзор часа пик» . ИГН ПК . ИГН Энтертейнмент, Инк . Архивировано из оригинала 20 сентября 2003 года . Проверено 10 января 2008 г.

[gamasutra_uol-25] Грили, Дэйв; Бен Сойер (19 августа 1997 г.). «Создала ли Origin первый настоящий мир онлайн-игр?» . Гамасутра . ООО «СМП Медиа» . Проверено 17 декабря 2007 г.

[26] Уокер, Трей (12 июля 2002 г.). «Divine Divinity становится золотом» . ГеймСпот . CBS Интерактив . Проверено 11 апреля 2017 г.

[cvg_ss-27] О'Хаган, Стив (7 августа 2008 г.). «Превью ПК: Silent Storm» . ComputerAndVideoGames.com . Фьючер Паблишинг Лимитед . Проверено 13 декабря 2007 г.

[tlight_gr-28] Макдугалл, Джаз (4 ноября 2009 г.). «Обзор Факела» . Игровой радар . Проверено 6 ноября 2009 г.

[29] Гамильтон, Кирк (3 июля 2014 г.). «Я рад, что они все еще делают такие игры, как Divinity: Original Sin» . Котаку . Медиагруппа Гизмодо . Проверено 11 апреля 2017 г.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]