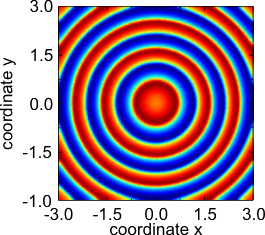
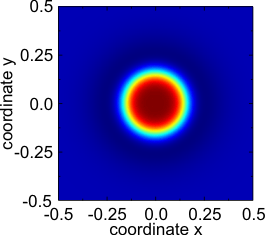
Реакционно-диффузионная система

Моделирование двух виртуальных химических веществ, реагирующих и диффундирующих на торе, с использованием модели Грея – Скотта.

Реакционно-диффузионные системы представляют собой математические модели, соответствующие нескольким физическим явлениям. Наиболее распространенным является изменение в пространстве и времени концентрации одного или нескольких химических веществ: локальные химические реакции, при которых вещества превращаются друг в друга, и диффузия , вызывающая распространение веществ по поверхности в пространстве.

Реакционно-диффузионные системы естественным образом применяются в химии . Однако система может описывать и динамические процессы нехимической природы. Примеры можно найти в биологии , геологии и физике (теория диффузии нейтронов) и экологии . Математически системы реакция-диффузия принимают форму полулинейных параболических уравнений в частных производных . Их можно представить в общем виде

\partial _{t}{\boldsymbol {q}}={\underline {\underline {\boldsymbol {D}}}}\,\nabla ^{2}{\boldsymbol {q}}+{\boldsymbol {R}}({\boldsymbol {q}}),

где $q (x, t)$ представляет собой неизвестную векторную функцию, $D$ - диагональная матрица коэффициентов диффузии , а $R$ учитывает все локальные реакции. Решения уравнений реакции-диффузии демонстрируют широкий спектр поведения, включая образование бегущих волн и волнообразных явлений, а также других самоорганизующихся структур, таких как полосы, шестиугольники или более сложные структуры, такие как диссипативные солитоны . Такие закономерности получили название « паттерны Тьюринга ». ^[1] Каждая функция, для которой выполняется дифференциальное уравнение реакции-диффузии, фактически представляет собой переменную концентрации .

Уравнения однокомпонентной реакции-диффузии.

Простейшее уравнение реакции-диффузии находится в одном пространственном измерении в плоской геометрии:

\partial _{t}u=D\partial _{x}^{2}u+R(u),

также называется уравнением Колмогорова–Петровского–Пискунова . ^[2] Если член реакции обращается в нуль, то уравнение представляет собой чистый диффузионный процесс. Соответствующее уравнение представляет собой второй закон Фика . Выбор $R (u) = u (1 - u)$ дает уравнение Фишера , которое первоначально использовалось для описания распространения биологических популяций : ^[3] уравнение Ньюэлла–Уайтхеда–Сигеля с $R (u) = u (1 - u 2)$ для описания конвекции Рэлея–Бенара , ^[4]^[5] более общее уравнение Зельдовича–Франка-Каменецкого с $R (u) = u (1 - u)e - б (1- у)$ и $0 < β < \infty$ ( число Зельдовича ), возникающее в теории горения , ^[6] и его частный вырожденный случай с $R (u) = u 2 - в 3$ его иногда также называют уравнением Зельдовича. ^[7]

Динамика однокомпонентных систем подвержена определенным ограничениям, поскольку уравнение эволюции можно записать и в вариационной форме

\partial _{t}u=-{\frac {\delta {\mathfrak {L}}}{\delta u}}

и, следовательно, описывает постоянное уменьшение «свободной энергии». ${\mathfrak {L}}$ заданный функционалом

{\mathfrak {L}}=\int _{-\infty }^{\infty }\left[{\tfrac {D}{2}}\left(\partial _{x}u\right)^{2}-V(u)\right]\,{\text{d}}x

с потенциалом $V (u)$ таким, что $R ( u ) = .mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion,.mw-parser-output .sfrac .tion{display:inline-block;vertical-align:-0.5em;font-size:85%;text-align:center}.mw-parser-output .sfrac .num{display:block;line-height:1em;margin:0.0em 0.1em;border-bottom:1px solid}.mw-parser-output .sfrac .den{display:block;line-height:1em;margin:0.1em 0.1em}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);clip-path:polygon(0px 0px,0px 0px,0px 0px);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px}⁠ d V ( ты ) / d ты ⁠ .$

В системах с более чем одним стационарным однородным решением типичным решением являются бегущие фронты, соединяющие однородные состояния. Эти решения движутся с постоянной скоростью, не меняя своей формы, и имеют вид $u (x, t) = û (ξ)$ с $ξ = x - ct$ , где $c$ — скорость бегущей волны. Обратите внимание, что хотя бегущие волны в целом являются устойчивыми структурами, все немонотонные стационарные решения (например, локализованные области, состоящие из пары фронт-антифрон) неустойчивы. Для $c = 0$ существует простое доказательство этого утверждения: ^[8] если $u 0 (x)$ является стационарным решением и $u = u 0 (x) + ũ (x, t)$ является бесконечно мало возмущенным решением, линейный анализ устойчивости дает уравнение

\partial _{t}{\tilde {u}}=D\partial _{x}^{2}{\tilde {u}}-U(x){\tilde {u}},\qquad U(x)=-R^{\prime }(u){\Big |}_{u=u_{0}(x)}.

Используя анзац $ũ = ψ (x)exp(- λt),$ мы приходим к проблеме собственных значений

{\hat {H}}\psi =\lambda \psi ,\qquad {\hat {H}}=-D\partial _{x}^{2}+U(x),

типа Шредингера , где отрицательные собственные значения приводят к неустойчивости решения. Благодаря трансляционной инвариантности $ψ = \partial x u 0 (x)$ является нейтральной собственной функцией с собственным значением $λ = 0$ , а все остальные собственные функции могут быть отсортированы по возрастающему числу узлов, при этом величина соответствующего действительного собственного значения монотонно возрастает с ростом числа узлов. количество нулей. Собственная функция $ψ = \partial x u 0 (x)$ должна иметь хотя бы один нуль, а для немонотонного стационарного решения соответствующее собственное значение $λ = 0$ не может быть наименьшим, что означает неустойчивость.

Чтобы определить скорость $c$ движущегося фронта, можно перейти к движущейся системе координат и посмотреть на стационарные решения:

D\partial _{\xi }^{2}{\hat {u}}(\xi )+c\partial _{\xi }{\hat {u}}(\xi )+R({\hat {u}}(\xi ))=0.

Это уравнение имеет хороший механический аналог — движение массы $D$ с положением $û$ в течение «времени» $ξ$ под действием силы $R$ с коэффициентом затухания с, что позволяет весьма наглядным образом получить доступ к построению различных типов решений. и определение $c$ .

При переходе от одного к нескольким измерениям пространства по-прежнему можно применять ряд утверждений одномерных систем. Плоские или изогнутые волновые фронты являются типичными структурами, и новый эффект возникает, когда локальная скорость искривленного фронта становится зависимой от локального радиуса кривизны (это можно увидеть, перейдя к полярным координатам ). Это явление приводит к так называемой неустойчивости, вызванной кривизной. ^[9]

Двухкомпонентные уравнения реакции-диффузии.

Двухкомпонентные системы допускают гораздо больший диапазон возможных явлений, чем их однокомпонентные аналоги. Важная идея, впервые предложенная Аланом Тьюрингом, заключается в том, что состояние, устойчивое в локальной системе, может стать нестабильным в присутствии диффузии . ^[10]

Однако анализ линейной устойчивости показывает, что при линеаризации общей двухкомпонентной системы

{\begin{pmatrix}\partial _{t}u\\\partial _{t}v\end{pmatrix}}={\begin{pmatrix}D_{u}&0\\0&D_{v}\end{pmatrix}}{\begin{pmatrix}\partial _{xx}u\\\partial _{xx}v\end{pmatrix}}+{\begin{pmatrix}F(u,v)\\G(u,v)\end{pmatrix}}

плосковолновое возмущение

{\tilde {\boldsymbol {q}}}_{\boldsymbol {k}}({\boldsymbol {x}},t)={\begin{pmatrix}{\tilde {u}}(t)\\{\tilde {v}}(t)\end{pmatrix}}e^{i{\boldsymbol {k}}\cdot {\boldsymbol {x}}}

стационарного однородного раствора будет удовлетворять

{\begin{pmatrix}\partial _{t}{\tilde {u}}_{\boldsymbol {k}}(t)\\\partial _{t}{\tilde {v}}_{\boldsymbol {k}}(t)\end{pmatrix}}=-k^{2}{\begin{pmatrix}D_{u}{\tilde {u}}_{\boldsymbol {k}}(t)\\D_{v}{\tilde {v}}_{\boldsymbol {k}}(t)\end{pmatrix}}+{\boldsymbol {R}}^{\prime }{\begin{pmatrix}{\tilde {u}}_{\boldsymbol {k}}(t)\\{\tilde {v}}_{\boldsymbol {k}}(t)\end{pmatrix}}.

Идея Тьюринга может быть реализована только в четырех классах эквивалентности систем, характеризующихся знаками якобиана R $' функции$ реакции. В частности, если конечный волновой вектор $k$ предполагается наиболее неустойчивым, то якобиан должен иметь знаки

{\begin{pmatrix}+&-\\+&-\end{pmatrix}},\quad {\begin{pmatrix}+&+\\-&-\end{pmatrix}},\quad {\begin{pmatrix}-&+\\-&+\end{pmatrix}},\quad {\begin{pmatrix}-&-\\+&+\end{pmatrix}}.

Этот класс систем назван системой активатор-ингибитор по имени своего первого представителя: вблизи основного состояния один компонент стимулирует продукцию обоих компонентов, а другой тормозит их рост. Его наиболее ярким представителем является уравнение ФитцХью – Нагумо.

{\begin{aligned}\partial _{t}u&=d_{u}^{2}\,\nabla ^{2}u+f(u)-\sigma v,\\\tau \partial _{t}v&=d_{v}^{2}\,\nabla ^{2}v+u-v\end{aligned}}

с $ж (ты) знак равно λu - ты 3 - κ$ , который описывает, как потенциал действия проходит через нерв. ^[11]^[12] Здесь $d u, d v, τ, σ$ и $λ$ — положительные константы.

При изменении параметров системы активатор-ингибитор можно перейти от условий, при которых однородное основное состояние устойчиво, к условиям, при которых оно линейно неустойчиво. Соответствующая бифуркация может быть либо бифуркацией Хопфа к глобально осциллирующему однородному состоянию с доминирующим волновым числом $k = 0$ , либо бифуркацией Тьюринга к состоянию с глобальным шаблоном и доминирующим конечным волновым числом. Последнее в двух пространственных измерениях обычно приводит к полосам или шестиугольным узорам.

Докритическая бифуркация Тьюринга: образование гексагональной структуры из зашумленных начальных условий в описанной выше двухкомпонентной реакционно-диффузионной системе типа Фицхью – Нагумо.
Шумные начальные условия при t = 0.
Состояние системы в момент t = 10.
Почти сходящееся состояние при t = 100.

Для примера Фитцхью – Нагумо нейтральные кривые устойчивости, обозначающие границу линейно устойчивой области для бифуркации Тьюринга и Хопфа, имеют вид

{\begin{aligned}q_{\text{n}}^{H}(k):&{}\quad {\frac {1}{\tau }}+\left(d_{u}^{2}+{\frac {1}{\tau }}d_{v}^{2}\right)k^{2}&=f^{\prime }(u_{h}),\\[6pt]q_{\text{n}}^{T}(k):&{}\quad {\frac {\kappa }{1+d_{v}^{2}k^{2}}}+d_{u}^{2}k^{2}&=f^{\prime }(u_{h}).\end{aligned}}

Если бифуркация докритическая, то часто локализованные структуры ( диссипативные солитоны ) можно наблюдать в гистерезисной области, где паттерн сосуществует с основным состоянием. Другие часто встречающиеся структуры включают последовательности импульсов (также известные как периодические бегущие волны ), спиральные волны и целевые структуры. Эти три типа решений также являются общими чертами двух- (или более) компонентных уравнений реакции-диффузии, в которых локальная динамика имеет устойчивый предельный цикл. ^[13]

Другие закономерности обнаружены в описанной выше двухкомпонентной реакционно-диффузионной системе типа Фитцхью – Нагумо.
Вращающаяся спираль.
Целевой шаблон.
Стационарный локализованный импульс (диссипативный солитон).

Трех- и более компонентные уравнения реакции-диффузии.

Для различных систем были предложены уравнения реакции-диффузии с более чем двумя компонентами, например реакция Белоусова-Жаботинского , ^[14] для свертывания крови , ^[15] волны деления ^[16] или плоские газоразрядные системы. ^[17]

Известно, что системы с большим количеством компонентов допускают множество явлений, невозможных в системах с одним или двумя компонентами (например, стабильные текущие импульсы в более чем одном пространственном измерении без глобальной обратной связи). ^[18] Введение и систематический обзор возможных явлений в зависимости от свойств базовой системы даются в . ^[19]

Приложения и универсальность

В последнее время системы реакции-диффузии вызвали большой интерес как прототип модели формирования структур . ^[20] Вышеупомянутые структуры (фронты, спирали, мишени, шестиугольники, полосы и диссипативные солитоны) можно обнаружить в различных типах реакционно-диффузионных систем, несмотря на большие различия, например, в терминах локальных реакций. Также утверждалось, что реакционно-диффузионные процессы являются важной основой процессов, связанных с морфогенезом в биологии. ^[21]^[22] и может даже быть связано с шерстью животных и пигментацией кожи. ^[23]^[24] Другие применения уравнений реакции-диффузии включают экологические вторжения, ^[25] распространение эпидемий, ^[26] рост опухоли, ^[27]^[28]^[29] динамика волн деления, ^[30] заживление ран ^[31] и зрительные галлюцинации. ^[32] Другая причина интереса к системам реакция-диффузия заключается в том, что, хотя они представляют собой нелинейные уравнения в частных производных, часто существуют возможности для аналитического рассмотрения. ^[8]^[9]^[33]^[34]^[35]^[20]

Эксперименты

Хорошо управляемые эксперименты в системах химической реакции-диффузии до сих пор реализовывались тремя способами. Во-первых, гелевые реакторы ^[36] или заполненные капилляры ^[37] можно использовать. Во-вторых, температурные импульсы на каталитических поверхностях . были исследованы ^[38]^[39] В-третьих, распространение бегущего нервного импульса моделируется с помощью реакционно-диффузионных систем. ^[11]^[40]

Помимо этих общих примеров, оказалось, что при соответствующих обстоятельствах системы электротранспорта, такие как плазменные ^[41] или полупроводники ^[42] можно описать с помощью реакционно-диффузионного подхода. Для этих систем были проведены различные эксперименты по формированию паттернов.

Численные методы лечения

Решить систему реакция-диффузия можно методами численной математики . В исследовательской литературе существует несколько численных методов лечения. ^[43]^[20]^[44] Также сложной геометрии . предложены методы численного решения ^[45]^[46] Реакционно-диффузионные системы с высочайшей степенью детализации описываются с помощью инструментов моделирования на основе частиц, таких как SRSim или ReaDDy. ^[47] которые используют, например обратимая динамика реакции взаимодействующих частиц. ^[48]

См. также

Примеры

Ссылки

^ Вули, Т.Э., Бейкер, Р.Э. , Майни, П.К. , Глава 34, Теория морфогенеза Тьюринга . В Коупленд, Б. Джек ; Боуэн, Джонатан П .; Уилсон, Робин ; Спревак, Марк (2017). Руководство Тьюринга . Издательство Оксфордского университета . ISBN 978-0198747826 .
^ Колмогоров А., Петровский И. и Пискунов Н. (1937) Исследование уравнения диффузии, связанного с ростом качества материи, и его применение к биологической проблеме. Вестник Московского математического университета, 1, 1-26.
^ Р. А. Фишер, Энн. Евг. 7 (1937): 355
^ Ньюэлл, Алан С.; Уайтхед, Дж. А. (3 сентября 1969 г.). «Конечная полоса пропускания, конвекция с конечной амплитудой». Журнал механики жидкости . 38 (2). Издательство Кембриджского университета (CUP): 279–303. Бибкод : 1969JFM....38..279N . дои : 10.1017/s0022112069000176 . ISSN 0022-1120 . S2CID 73620481 .
^ Сигел, Ли А. (14 августа 1969 г.). «Удаленные боковые стенки вызывают медленную амплитудную модуляцию клеточной конвекции». Журнал механики жидкости . 38 (1). Издательство Кембриджского университета (CUP): 203–224. Бибкод : 1969JFM....38..203S . дои : 10.1017/s0022112069000127 . ISSN 0022-1120 . S2CID 122764449 .
^ Ю.Б. Зельдович и Д.А. Франк-Каменецкий, Acta Physicochim. 9 (1938): 341
^ Б. Х. Гилдинг и Р. Керснер, Бегущие волны в нелинейной реакции диффузионной конвекции , Биркхойзер (2004).
^ Перейти обратно: ^а ^б ПК Файф, Математические аспекты реагирующих и диффузионных систем , Springer (1979).
^ Перейти обратно: ^а ^б А. С. Михайлов, Основы синергетики I. Распределенные активные системы, Springer (1990).
^ Тьюринг, AM (14 августа 1952 г.). «Химические основы морфогенеза» . Философские труды Лондонского королевского общества. Серия Б, Биологические науки . 237 (641). Королевское общество: 37–72. Бибкод : 1952РСПТБ.237...37Т . дои : 10.1098/rstb.1952.0012 . ISSN 2054-0280 .
^ Перейти обратно: ^а ^б ФитцХью, Ричард (1961). «Импульсы и физиологические состояния в теоретических моделях нервной мембраны» . Биофизический журнал . 1 (6). Эльзевир Б.В.: 445–466. Бибкод : 1961BpJ.....1..445F . дои : 10.1016/s0006-3495(61)86902-6 . ISSN 0006-3495 . ПМЦ 1366333 . ПМИД 19431309 .
^ Дж. Нагумо и др., Proc. Радиоинженерный институт. Электр. 50 (1962): 2061
^ Копелл, Н.; Ховард, Л.Н. (1973). «Решения плоских волн для уравнений реакции-диффузии». Исследования по прикладной математике . 52 (4). Уайли: 291–328. дои : 10.1002/sapm1973524291 . ISSN 0022-2526 .
^ Ванаг, Владимир К.; Эпштейн, Ирвинг Р. (24 марта 2004 г.). «Стационарные и колебательные локализованные закономерности и докритические бифуркации». Письма о физических отзывах . 92 (12). Американское физическое общество (APS): 128301. Бибкод : 2004PhRvL..92l8301V . дои : 10.1103/physrevlett.92.128301 . ISSN 0031-9007 . ПМИД 15089714 .
^ Лобанова Е.С.; Атауллаханов Ф.И. (26 августа 2004 г.). «Бегущие импульсы сложной формы в модели реакции-диффузии». Письма о физических отзывах . 93 (9). Американское физическое общество (APS): 098303. Бибкод : 2004PhRvL..93i8303L . doi : 10.1103/physrevlett.93.098303 . ISSN 0031-9007 . ПМИД 15447151 .
^ Осборн, AG; Ректенвальд, Германия; Дейнерт, MR (июнь 2012 г.). «Распространение уединенной волны деления» . Хаос: междисциплинарный журнал нелинейной науки . 22 (2): 023148. Бибкод : 2012Хаос..22b3148O . дои : 10.1063/1.4729927 . hdl : 2152/43281 . ISSN 1054-1500 . ПМИД 22757555 .
^ Х.-Г. Пурвинс и др. в: Диссипативные солитоны, Конспект лекций по физике, Под ред. Н. Ахмедиев и А. Анкевич, Springer (2005).
^ Шенк, КП; Ор-Гиль, М.; Боде, М.; Пурвинс, Х.-Г. (12 мая 1997 г.). «Взаимодействующие импульсы в трехкомпонентных реакционно-диффузионных системах в двумерных областях». Письма о физических отзывах . 78 (19). Американское физическое общество (APS): 3781–3784. Бибкод : 1997PhRvL..78.3781S . дои : 10.1103/physrevlett.78.3781 . ISSN 0031-9007 .
^ AW Liehr: Диссипативные солитоны в реакционно-диффузионных системах. Механизм, динамика, взаимодействие. Том 70 серии Springer по синергетике, Springer, Берлин, Гейдельберг, 2013, ISBN 978-3-642-31250-2
^ Перейти обратно: ^а ^б ^с Гупта, Анкур; Чакраборти, Сайкат (январь 2009 г.). «Анализ линейной устойчивости моделей высокой и низкой размерности для описания формирования структуры, ограниченной смешиванием, в гомогенных автокаталитических реакторах». Химико-технологический журнал . 145 (3): 399–411. doi : 10.1016/j.cej.2008.08.025 . ISSN 1385-8947 .
^ Л.Г. Харрисон, Кинетическая теория образа жизни, издательство Кембриджского университета (1993)
^ Дюран-Небреда, Сальва; Пла, Джордж; Видиэлла, Блай; Пиньеро, Хорди; Конде-Пуэйо, Нурия; Соле, Рикар (15 января 2021 г.). «Синтетическое латеральное ингибирование в периодическом формировании микробных колоний» . ACS Синтетическая биология . 10 (2): 277–285. doi : 10.1021/acsynbio.0c00318 . ISSN 2161-5063 . ПМЦ 8486170 . ПМИД 33449631 .
^ Х. Мейнхардт, Модели формирования биологических закономерностей, Academic Press (1982)
^ Мюррей, Джеймс Д. (9 марта 2013 г.). Математическая биология . Springer Science & Business Media. стр. 436–450. ISBN 978-3-662-08539-4 .
^ Холмс, Э.Э.; Льюис, Массачусетс; Бэнкс, Дж. Э.; Вейт, Р.Р. (1994). «Уравнения с частными производными в экологии: пространственные взаимодействия и динамика численности населения». Экология . 75 (1). Уайли: 17–29. дои : 10.2307/1939378 . ISSN 0012-9658 . JSTOR 1939378 . S2CID 85421773 .
^ Мюррей, Джеймс Д.; Стэнли, Э.А.; Браун, Д.Л. (22 ноября 1986 г.). «О пространственном распространении бешенства среди лисиц». Труды Лондонского королевского общества. Серия Б. Биологические науки . 229 (1255). Королевское общество: 111–150. Бибкод : 1986РСПСБ.229..111М . дои : 10.1098/rspb.1986.0078 . ISSN 2053-9193 . ПМИД 2880348 . S2CID 129301761 .
^ Капеллан, MAJ (1995). «Реакционно-диффузионный препаттерн и его потенциальная роль в инвазии опухоли». Журнал биологических систем . 03 (4). World Scientific Pub Co Pte Lt: 929–936. дои : 10.1142/s0218339095000824 . ISSN 0218-3390 .
^ Шерратт, Дж.А.; Новак, Массачусетс (22 июня 1992 г.). «Онкогены, антионкогены и иммунный ответ на рак: математическая модель». Труды Королевского общества B: Биологические науки . 248 (1323). Королевское общество: 261–271. дои : 10.1098/rspb.1992.0071 . ISSN 0962-8452 . ПМИД 1354364 . S2CID 11967813 .
^ Р. А. Гатенби и Э. Т. Гавлински, Cancer Res. 56 (1996): 5745
^ Осборн, Эндрю Г.; Дейнерт, Марк Р. (октябрь 2021 г.). «Неустойчивость стабильности и бифуркация Хопфа в волнах деления» . Отчеты о клетках Физические науки . 2 (10): 100588. Бибкод : 2021CRPS....200588O . дои : 10.1016/j.xcrp.2021.100588 . S2CID 240589650 .
^ Шерратт, Дж.А.; Мюррей, доктор юридических наук (23 июля 1990 г.). «Модели заживления эпидермальных ран». Труды Королевского общества B: Биологические науки . 241 (1300). Королевское общество: 29–36. дои : 10.1098/rspb.1990.0061 . ISSN 0962-8452 . ПМИД 1978332 . S2CID 20717487 .
^ https://www.quantamagazine.org/a-math-theory-for-why-people-hallucinate-20180730/
^ П. Гриндрод, Паттерны и волны: теория и применение уравнений реакции-диффузии, Clarendon Press (1991)
^ Дж. Смоллер, Ударные волны и уравнения реакции-диффузии, Springer (1994)
^ Б. С. Кернер, В. В. Осипов, Автосолитоны. Новый подход к проблемам самоорганизации и турбулентности, Kluwer Academic Publishers (1994).
^ Ли, Кён Джин; Маккормик, Уильям Д.; Пирсон, Джон Э.; Суинни, Гарри Л. (1994). «Экспериментальное наблюдение самовоспроизводящихся пятен в системе реакция-диффузия». Природа . 369 (6477). Спрингер Природа: 215–218. Бибкод : 1994Natur.369..215L . дои : 10.1038/369215a0 . ISSN 0028-0836 . S2CID 4257570 .
^ Хамик, Чад Т; Стейнбок, Оливер (6 июня 2003 г.). «Волны возбуждения в реакционно-диффузионных средах с немонотонными дисперсионными соотношениями» . Новый журнал физики . 5 (1). Издательство IOP: 58. Бибкод : 2003NJPh....5...58H . дои : 10.1088/1367-2630/5/1/358 . ISSN 1367-2630 .
^ Ротермунд, ХХ; Якубит, С.; фон Эрцен, А.; Эртль, Г. (10 июня 1991 г.). «Солитоны в поверхностной реакции». Письма о физических отзывах . 66 (23). Американское физическое общество (APS): 3083–3086. Бибкод : 1991PhRvL..66.3083R . дои : 10.1103/physrevlett.66.3083 . ISSN 0031-9007 . ПМИД 10043694 .
^ Грэм, Майкл Д.; Лейн, Сэмюэл Л.; Лусс, Дэн (1993). «Динамика температурных импульсов на каталитическом кольце». Журнал физической химии . 97 (29). Американское химическое общество (ACS): 7564–7571. дои : 10.1021/j100131a028 . ISSN 0022-3654 .
^ Ходжкин, Алабама; Хаксли, AF (28 августа 1952 г.). «Количественное описание мембранного тока и его применение к проводимости и возбуждению нерва» . Журнал физиологии . 117 (4). Уайли: 500–544. doi : 10.1113/jphysicalol.1952.sp004764 . ISSN 0022-3751 . ПМК 1392413 . ПМИД 12991237 .
^ Боде, М.; Пурвинс, Х.-Г. (1995). «Формирование узоров в реакционно-диффузионных системах - диссипативные солитоны в физических системах». Физика D: Нелинейные явления . 86 (1–2). Эльзевир Б.В.: 53–63. Бибкод : 1995PhyD...86...53B . дои : 10.1016/0167-2789(95)00087-к . ISSN 0167-2789 .
^ Э. Шёлль, Нелинейная пространственно-временная динамика и хаос в полупроводниках, Cambridge University Press (2001)
^ S.Tang et al., J.Austral.Math.Soc. Сер.Б 35 (1993): 223–243.
^ Тим Хаттон, Роберт Мунафо, Эндрю Треворроу, Том Рокики, Дэн Уиллс. «Готово, кросс-платформенная реализация различных систем реакции-диффузии». https://github.com/GollyGang/ready
^ Исааксон, Сэмюэл А.; Пескин, Чарльз С. (2006). «Включение диффузии в сложной геометрии в моделирование стохастической химической кинетики». СИАМ J. Sci. Вычислить . 28 (1): 47–74. Бибкод : 2006ГАК...28...47И . CiteSeerX 10.1.1.105.2369 . дои : 10.1137/040605060 .
^ Линкер, Патрик (2016). «Численные методы решения уравнения реактивной диффузии в сложных геометриях» . Веялка .
^ Инструменты моделирования динамики реакции-диффузии на основе частиц в непрерывном пространстве https://link.springer.com/article/10.1186/s13628-014-0011-5
^ Фрёнер, Кристоф и Фрэнк Ноэ. «Динамика реакции обратимых взаимодействующих частиц». Журнал физической химии B 122.49 (2018): 11240-11250.

Внешние ссылки

Реакция-диффузия по модели Грея-Скотта: параметризация Пирсона - визуальная карта пространства параметров реакционной диффузии Грея-Скотта.
Диссертация по закономерностям реакции-диффузии с обзором области.
RD Tool: интерактивное веб-приложение для моделирования реакции-диффузии.

[1] Вули, Т.Э., Бейкер, Р.Э. , Майни, П.К. , Глава 34, Теория морфогенеза Тьюринга . В Коупленд, Б. Джек ; Боуэн, Джонатан П .; Уилсон, Робин ; Спревак, Марк (2017). Руководство Тьюринга . Издательство Оксфордского университета . ISBN 978-0198747826 .

[2] Колмогоров А., Петровский И. и Пискунов Н. (1937) Исследование уравнения диффузии, связанного с ростом качества материи, и его применение к биологической проблеме. Вестник Московского математического университета, 1, 1-26.

[3] Р. А. Фишер, Энн. Евг. 7 (1937): 355

[4] Ньюэлл, Алан С.; Уайтхед, Дж. А. (3 сентября 1969 г.). «Конечная полоса пропускания, конвекция с конечной амплитудой». Журнал механики жидкости . 38 (2). Издательство Кембриджского университета (CUP): 279–303. Бибкод : 1969JFM....38..279N . дои : 10.1017/s0022112069000176 . ISSN 0022-1120 . S2CID 73620481 .

[5] Сигел, Ли А. (14 августа 1969 г.). «Удаленные боковые стенки вызывают медленную амплитудную модуляцию клеточной конвекции». Журнал механики жидкости . 38 (1). Издательство Кембриджского университета (CUP): 203–224. Бибкод : 1969JFM....38..203S . дои : 10.1017/s0022112069000127 . ISSN 0022-1120 . S2CID 122764449 .

[6] Ю.Б. Зельдович и Д.А. Франк-Каменецкий, Acta Physicochim. 9 (1938): 341

[7] Б. Х. Гилдинг и Р. Керснер, Бегущие волны в нелинейной реакции диффузионной конвекции , Биркхойзер (2004).

[fife-8] Перейти обратно: ^а ^б ПК Файф, Математические аспекты реагирующих и диффузионных систем , Springer (1979).

[mikhailov-9] Перейти обратно: ^а ^б А. С. Михайлов, Основы синергетики I. Распределенные активные системы, Springer (1990).

[10] Тьюринг, AM (14 августа 1952 г.). «Химические основы морфогенеза» . Философские труды Лондонского королевского общества. Серия Б, Биологические науки . 237 (641). Королевское общество: 37–72. Бибкод : 1952РСПТБ.237...37Т . дои : 10.1098/rstb.1952.0012 . ISSN 2054-0280 .

[fitzhugh-11] Перейти обратно: ^а ^б ФитцХью, Ричард (1961). «Импульсы и физиологические состояния в теоретических моделях нервной мембраны» . Биофизический журнал . 1 (6). Эльзевир Б.В.: 445–466. Бибкод : 1961BpJ.....1..445F . дои : 10.1016/s0006-3495(61)86902-6 . ISSN 0006-3495 . ПМЦ 1366333 . ПМИД 19431309 .

[12] Дж. Нагумо и др., Proc. Радиоинженерный институт. Электр. 50 (1962): 2061

[13] Копелл, Н.; Ховард, Л.Н. (1973). «Решения плоских волн для уравнений реакции-диффузии». Исследования по прикладной математике . 52 (4). Уайли: 291–328. дои : 10.1002/sapm1973524291 . ISSN 0022-2526 .

[14] Ванаг, Владимир К.; Эпштейн, Ирвинг Р. (24 марта 2004 г.). «Стационарные и колебательные локализованные закономерности и докритические бифуркации». Письма о физических отзывах . 92 (12). Американское физическое общество (APS): 128301. Бибкод : 2004PhRvL..92l8301V . дои : 10.1103/physrevlett.92.128301 . ISSN 0031-9007 . ПМИД 15089714 .

[15] Лобанова Е.С.; Атауллаханов Ф.И. (26 августа 2004 г.). «Бегущие импульсы сложной формы в модели реакции-диффузии». Письма о физических отзывах . 93 (9). Американское физическое общество (APS): 098303. Бибкод : 2004PhRvL..93i8303L . doi : 10.1103/physrevlett.93.098303 . ISSN 0031-9007 . ПМИД 15447151 .

[16] Осборн, AG; Ректенвальд, Германия; Дейнерт, MR (июнь 2012 г.). «Распространение уединенной волны деления» . Хаос: междисциплинарный журнал нелинейной науки . 22 (2): 023148. Бибкод : 2012Хаос..22b3148O . дои : 10.1063/1.4729927 . hdl : 2152/43281 . ISSN 1054-1500 . ПМИД 22757555 .

[17] Х.-Г. Пурвинс и др. в: Диссипативные солитоны, Конспект лекций по физике, Под ред. Н. Ахмедиев и А. Анкевич, Springer (2005).

[18] Шенк, КП; Ор-Гиль, М.; Боде, М.; Пурвинс, Х.-Г. (12 мая 1997 г.). «Взаимодействующие импульсы в трехкомпонентных реакционно-диффузионных системах в двумерных областях». Письма о физических отзывах . 78 (19). Американское физическое общество (APS): 3781–3784. Бибкод : 1997PhRvL..78.3781S . дои : 10.1103/physrevlett.78.3781 . ISSN 0031-9007 .

[19] AW Liehr: Диссипативные солитоны в реакционно-диффузионных системах. Механизм, динамика, взаимодействие. Том 70 серии Springer по синергетике, Springer, Берлин, Гейдельберг, 2013, ISBN 978-3-642-31250-2

[:0-20] Перейти обратно: ^а ^б ^с Гупта, Анкур; Чакраборти, Сайкат (январь 2009 г.). «Анализ линейной устойчивости моделей высокой и низкой размерности для описания формирования структуры, ограниченной смешиванием, в гомогенных автокаталитических реакторах». Химико-технологический журнал . 145 (3): 399–411. doi : 10.1016/j.cej.2008.08.025 . ISSN 1385-8947 .

[21] Л.Г. Харрисон, Кинетическая теория образа жизни, издательство Кембриджского университета (1993)

[22] Дюран-Небреда, Сальва; Пла, Джордж; Видиэлла, Блай; Пиньеро, Хорди; Конде-Пуэйо, Нурия; Соле, Рикар (15 января 2021 г.). «Синтетическое латеральное ингибирование в периодическом формировании микробных колоний» . ACS Синтетическая биология . 10 (2): 277–285. doi : 10.1021/acsynbio.0c00318 . ISSN 2161-5063 . ПМЦ 8486170 . ПМИД 33449631 .

[23] Х. Мейнхардт, Модели формирования биологических закономерностей, Academic Press (1982)

[Murray2013-24] Мюррей, Джеймс Д. (9 марта 2013 г.). Математическая биология . Springer Science & Business Media. стр. 436–450. ISBN 978-3-662-08539-4 .

[25] Холмс, Э.Э.; Льюис, Массачусетс; Бэнкс, Дж. Э.; Вейт, Р.Р. (1994). «Уравнения с частными производными в экологии: пространственные взаимодействия и динамика численности населения». Экология . 75 (1). Уайли: 17–29. дои : 10.2307/1939378 . ISSN 0012-9658 . JSTOR 1939378 . S2CID 85421773 .

[26] Мюррей, Джеймс Д.; Стэнли, Э.А.; Браун, Д.Л. (22 ноября 1986 г.). «О пространственном распространении бешенства среди лисиц». Труды Лондонского королевского общества. Серия Б. Биологические науки . 229 (1255). Королевское общество: 111–150. Бибкод : 1986РСПСБ.229..111М . дои : 10.1098/rspb.1986.0078 . ISSN 2053-9193 . ПМИД 2880348 . S2CID 129301761 .

[27] Капеллан, MAJ (1995). «Реакционно-диффузионный препаттерн и его потенциальная роль в инвазии опухоли». Журнал биологических систем . 03 (4). World Scientific Pub Co Pte Lt: 929–936. дои : 10.1142/s0218339095000824 . ISSN 0218-3390 .

[28] Шерратт, Дж.А.; Новак, Массачусетс (22 июня 1992 г.). «Онкогены, антионкогены и иммунный ответ на рак: математическая модель». Труды Королевского общества B: Биологические науки . 248 (1323). Королевское общество: 261–271. дои : 10.1098/rspb.1992.0071 . ISSN 0962-8452 . ПМИД 1354364 . S2CID 11967813 .

[29] Р. А. Гатенби и Э. Т. Гавлински, Cancer Res. 56 (1996): 5745

[Osborne_100588-30] Осборн, Эндрю Г.; Дейнерт, Марк Р. (октябрь 2021 г.). «Неустойчивость стабильности и бифуркация Хопфа в волнах деления» . Отчеты о клетках Физические науки . 2 (10): 100588. Бибкод : 2021CRPS....200588O . дои : 10.1016/j.xcrp.2021.100588 . S2CID 240589650 .

[31] Шерратт, Дж.А.; Мюррей, доктор юридических наук (23 июля 1990 г.). «Модели заживления эпидермальных ран». Труды Королевского общества B: Биологические науки . 241 (1300). Королевское общество: 29–36. дои : 10.1098/rspb.1990.0061 . ISSN 0962-8452 . ПМИД 1978332 . S2CID 20717487 .

[32] ttps://www.quantamagazine.org/a-math-theory-for-why-people-hallucinate-20180730/

[33] П. Гриндрод, Паттерны и волны: теория и применение уравнений реакции-диффузии, Clarendon Press (1991)

[34] Дж. Смоллер, Ударные волны и уравнения реакции-диффузии, Springer (1994)

[35] Б. С. Кернер, В. В. Осипов, Автосолитоны. Новый подход к проблемам самоорганизации и турбулентности, Kluwer Academic Publishers (1994).

[36] Ли, Кён Джин; Маккормик, Уильям Д.; Пирсон, Джон Э.; Суинни, Гарри Л. (1994). «Экспериментальное наблюдение самовоспроизводящихся пятен в системе реакция-диффузия». Природа . 369 (6477). Спрингер Природа: 215–218. Бибкод : 1994Natur.369..215L . дои : 10.1038/369215a0 . ISSN 0028-0836 . S2CID 4257570 .

[37] Хамик, Чад Т; Стейнбок, Оливер (6 июня 2003 г.). «Волны возбуждения в реакционно-диффузионных средах с немонотонными дисперсионными соотношениями» . Новый журнал физики . 5 (1). Издательство IOP: 58. Бибкод : 2003NJPh....5...58H . дои : 10.1088/1367-2630/5/1/358 . ISSN 1367-2630 .

[38] Ротермунд, ХХ; Якубит, С.; фон Эрцен, А.; Эртль, Г. (10 июня 1991 г.). «Солитоны в поверхностной реакции». Письма о физических отзывах . 66 (23). Американское физическое общество (APS): 3083–3086. Бибкод : 1991PhRvL..66.3083R . дои : 10.1103/physrevlett.66.3083 . ISSN 0031-9007 . ПМИД 10043694 .

[39] Грэм, Майкл Д.; Лейн, Сэмюэл Л.; Лусс, Дэн (1993). «Динамика температурных импульсов на каталитическом кольце». Журнал физической химии . 97 (29). Американское химическое общество (ACS): 7564–7571. дои : 10.1021/j100131a028 . ISSN 0022-3654 .

[40] Ходжкин, Алабама; Хаксли, AF (28 августа 1952 г.). «Количественное описание мембранного тока и его применение к проводимости и возбуждению нерва» . Журнал физиологии . 117 (4). Уайли: 500–544. doi : 10.1113/jphysicalol.1952.sp004764 . ISSN 0022-3751 . ПМК 1392413 . ПМИД 12991237 .

[41] Боде, М.; Пурвинс, Х.-Г. (1995). «Формирование узоров в реакционно-диффузионных системах - диссипативные солитоны в физических системах». Физика D: Нелинейные явления . 86 (1–2). Эльзевир Б.В.: 53–63. Бибкод : 1995PhyD...86...53B . дои : 10.1016/0167-2789(95)00087-к . ISSN 0167-2789 .

[42] Э. Шёлль, Нелинейная пространственно-временная динамика и хаос в полупроводниках, Cambridge University Press (2001)

[43] S.Tang et al., J.Austral.Math.Soc. Сер.Б 35 (1993): 223–243.

[44] Тим Хаттон, Роберт Мунафо, Эндрю Треворроу, Том Рокики, Дэн Уиллс. «Готово, кросс-платформенная реализация различных систем реакции-диффузии». https://github.com/GollyGang/ready

[45] Исааксон, Сэмюэл А.; Пескин, Чарльз С. (2006). «Включение диффузии в сложной геометрии в моделирование стохастической химической кинетики». СИАМ J. Sci. Вычислить . 28 (1): 47–74. Бибкод : 2006ГАК...28...47И . CiteSeerX 10.1.1.105.2369 . дои : 10.1137/040605060 .

[46] Линкер, Патрик (2016). «Численные методы решения уравнения реактивной диффузии в сложных геометриях» . Веялка .

[47] Инструменты моделирования динамики реакции-диффузии на основе частиц в непрерывном пространстве https://link.springer.com/article/10.1186/s13628-014-0011-5

[48] Фрёнер, Кристоф и Фрэнк Ноэ. «Динамика реакции обратимых взаимодействующих частиц». Журнал физической химии B 122.49 (2018): 11240-11250.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

[30]

[31]

[32]

[33]

[34]

[35]

[36]

[37]

[38]

[39]

[40]

[41]

[42]

[43]

[44]

[45]

[46]

[47]

[48]