✖


Jump to content

Многосостояние моделирования биомолекул

Эта статья была опубликована в рецензируемом журнале PLOS Computational Biology (2014). Нажмите, чтобы просмотреть опубликованную версию.

Моделирование биомолекул с несколькими состояниями относится к серии методов, используемых для представления и расчета поведения биологических молекул или комплексов , которые могут принимать большое количество возможных функциональных состояний.

Биологические сигнальные системы часто опираются на комплексы биологических макромолекул , которые могут претерпевать несколько функционально значимых модификаций, взаимно совместимых. Таким образом, они могут существовать в очень большом количестве функционально различных состояний. Моделирование таких систем с несколькими состояниями ставит две проблемы: проблему того, как описать и указать систему с несколькими состояниями («проблема спецификации») и проблему того, как использовать компьютер для моделирования развития системы с течением времени («проблема спецификации»). «вычислительная задача»). Чтобы решить проблему спецификации, разработчики моделей в последние годы отошли от явной спецификации всех возможных состояний и перешли к моделированию на основе правил , которое допускает неявную спецификацию модели, включая κ-исчисление, [1] БиоНетГен , [2] [3] [4] [5] компилятор аллостерических сетей [6] и другие. [7] [8] Чтобы решить проблему вычислений, они обратились к методам, основанным на частицах, которые во многих случаях оказались более эффективными в вычислительном отношении, чем методы, основанные на популяциях, основанные на обыкновенных дифференциальных уравнениях , уравнениях в частных производных или алгоритме стохастического моделирования Гиллеспи . [9] [10] Учитывая современные вычислительные технологии, методы на основе частиц иногда являются единственным возможным вариантом. Симуляторы на основе частиц делятся на две категории: непространственные симуляторы , такие как StochSim, [11] ДИНСТОК, [12] ПравилоОбезьяна, [9] [13] и НФСим [14] и пространственные тренажеры, [15] включая Мередиса, [16] СРСим [17] [18] и MCell. [19] [20] [21] Таким образом, разработчики моделей могут выбирать из множества инструментов; лучший выбор в зависимости от конкретной проблемы. Продолжается разработка более быстрых и мощных методов, обещающих возможность моделировать еще более сложные сигнальные процессы в будущем.

Введение

[ редактировать ]

Биомолекулы с несколькими состояниями в передаче сигнала

[ редактировать ]

В живых клетках сигналы обрабатываются сетями белков , которые могут действовать как сложные вычислительные устройства. [22] Эти сети основаны на способности отдельных белков существовать в различных функционально различных состояниях, достигаемых посредством множества механизмов, включая посттрансляционные модификации , связывание лигандов , конформационные изменения или образование новых комплексов . [22] [23] [24] [25] Точно так же нуклеиновые кислоты могут подвергаться множеству трансформаций, включая связывание с белками, связывание других нуклеиновых кислот, конформационные изменения и метилирование ДНК .

Кроме того, могут сосуществовать несколько типов модификаций, оказывающих комплексное влияние на биологическую макромолекулу в любой момент времени. Таким образом, биомолекула или комплекс биомолекул часто могут принимать очень большое количество функционально различных состояний. Число состояний растет экспоненциально с количеством возможных модификаций — явление, известное как « комбинаторный взрыв ». [25] Это вызывает беспокойство у компьютерных биологов, которые моделируют или моделируют такие биомолекулы, поскольку поднимает вопросы о том, как можно представить и смоделировать такое большое количество состояний.

Примеры комбинаторного взрыва

[ редактировать ]

Биологические сигнальные сети включают в себя широкий спектр обратимых взаимодействий , посттрансляционных модификаций и конформационных изменений . Более того, обычно белок состоит из нескольких идентичных или неидентичных субъединиц , а несколько белков и/или видов нуклеиновых кислот собираются в более крупные комплексы. Таким образом, молекулярные виды с некоторыми из этих особенностей могут существовать в большом количестве возможных состояний.

Например, было подсчитано, что дрожжевой каркасный белок Ste5 может входить в состав 25666 уникальных белковых комплексов. [23] У E. coli рецепторы хемотаксиса четырех разных типов взаимодействуют группами по три, причем каждый отдельный рецептор может существовать как минимум в двух возможных конформациях и иметь до восьми метилирования . сайтов [24] в результате чего возникают миллиарды потенциальных состояний. Протеинкиназа каталитических CaMKII представляет собой додекамер двенадцати из субъединиц. [26] расположены в виде двух гексамерных колец. [27] Каждая субъединица может существовать по крайней мере в двух различных конформациях, и каждая субъединица имеет различные сайты фосфорилирования и связывания лигандов. Последняя модель [28] включены конформационные состояния, два сайта фосфорилирования и два способа связывания кальция/кальмодулина , всего около одного миллиарда возможных состояний на гексамерное кольцо. Модель соединения рецептора EGF с каскадом киназы MAP , представленная Даносом и его коллегами. [29] приходится на отдельные молекулярные виды, однако авторы отмечают несколько моментов, в которых модель может быть расширена. Более поздняя модель передачи сигналов рецептора ErbB даже учитывает более одного гугола ( ) отдельные молекулярные виды. [30] Проблема комбинаторного взрыва актуальна и для синтетической биологии : недавно была разработана модель относительно простой синтетической эукариот генной цепи , включающей 187 видов и 1165 реакций . [31]

Конечно, не все возможные состояния многосостоящей молекулы или комплекса обязательно будут заселены. Действительно, в системах, где число возможных состояний намного больше, чем у молекул в отсеке (например, в клетке), их быть не может. В некоторых случаях эмпирическая информация может использоваться для исключения определенных состояний, если, например, некоторые комбинации признаков несовместимы. Однако при отсутствии такой информации все возможные состояния необходимо рассматривать априори . В таких случаях можно использовать компьютерное моделирование, чтобы выяснить, в какой степени заселены различные состояния.

Существование (или потенциальное существование) такого большого числа молекулярных видов является комбинаторным явлением: оно возникает из относительно небольшого набора особенностей или модификаций (таких как посттрансляционная модификация или образование комплекса), которые в совокупности диктуют состояние всей совокупности. молекула или комплекс, точно так же, как существование всего лишь нескольких вариантов выбора в кофейне (маленький, средний или большой, с молоком или без него, без кофеина или без него, дополнительная порция эспрессо ) быстро приводит к большому количеству возможных напитков. (в данном случае 24; каждый дополнительный двоичный выбор удваивает это число). Хотя нам трудно уловить общее количество возможных комбинаций, обычно концептуально нетрудно понять (гораздо меньший) набор особенностей или модификаций и влияние каждой из них на функцию биомолекулы. Скорость, с которой молекула подвергается определенной реакции, обычно зависит главным образом от одного признака или небольшого подмножества признаков. Именно наличие или отсутствие этих особенностей определяет скорость реакции . Скорость реакции одинакова для двух молекул, различающихся лишь признаками, не влияющими на эту реакцию. Таким образом, количество параметров будет намного меньше количества реакций. (В примере с кофейней добавление дополнительной порции эспрессо будет стоить 40 центов, независимо от размера напитка и наличия в нем молока). Именно такие «локальные правила» обычно обнаруживаются в лабораторных экспериментах. Таким образом, модель с несколькими государствами может быть концептуализирована как комбинация модульных функций и местных правил. Это означает, что даже модель, которая может объяснить огромное количество молекулярных видов и реакций, не обязательно является концептуально сложной.

Спецификация против вычислений

[ редактировать ]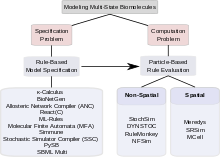
Обзор обсуждаемых инструментов, которые используются для спецификации на основе правил и оценки на основе частиц (пространственной или непространственной) биомолекул с несколькими состояниями.

Комбинаторная сложность сигнальных систем, включающих белки с несколькими состояниями, создает проблемы двух типов. Первая проблема связана с тем, как можно определить такую ​​систему; т.е. как разработчик модели может указать все комплексы, все изменения, которым подвергаются эти комплексы, а также все параметры и условия, управляющие этими изменениями надежным и эффективным способом. Эта проблема называется «проблемой спецификации». Вторая проблема касается вычислений . Он задает вопросы о том, является ли комбинаторно сложная модель, однажды заданная, вычислительно приемлемой, учитывая большое количество состояний и еще большее количество возможных переходов между состояниями, можно ли ее хранить в электронном виде и можно ли ее оценить в разумных пределах. количество вычислительного времени. Эта проблема называется «задачой вычислений». Среди подходов, которые были предложены для решения комбинаторной сложности в моделировании с несколькими состояниями, некоторые в основном связаны с решением проблемы спецификации, некоторые сосредоточены на поиске эффективных методов вычислений. Некоторые инструменты предназначены как для спецификации, так и для вычислений. В разделах ниже обсуждаются подходы, основанные на правилах, к проблеме спецификации и подходы, основанные на частицах, к решению проблемы вычислений. Для моделирования нескольких состояний существует широкий спектр вычислительных инструментов. [32]

Проблема со спецификацией

[ редактировать ]

Явная спецификация

[ редактировать ]

Самый наивный способ специфицировать, например, белок в биологической модели — это явно указать каждое из его состояний и использовать каждое из них в качестве молекулярной разновидности в рамках моделирования , допускающего переходы из состояния в состояние. Например, если белок может быть связан с лигандом или нет, существовать в двух конформационных состояниях (например, открытом или закрытом) и располагаться в двух возможных субклеточных областях (например, цитозольной или связанной с мембраной ), то восемь возможных результирующих состояний могут быть явно перечисляется как:

  • связанный, открытый, цитозольный
  • связанный, открытый, мембранный
  • связанный, закрытый, цитозольный
  • связанный, закрытый, мембранный
  • несвязанный, открытый, цитозольный
  • несвязанный, открытый, мембранный
  • несвязанный, закрытый, цитозольный
  • несвязанный, закрытый, мембранный

Перечисление всех возможных состояний — длительный и потенциально чреватый ошибками процесс. Для макромолекулярных комплексов, которые могут принимать несколько состояний, перечисление каждого состояния быстро становится утомительным, а то и невозможным. Более того, добавление одной дополнительной модификации или признака в модель исследуемого комплекса удвоит число возможных состояний (если модификация бинарная) и более чем вдвое увеличит количество переходов, которые необходимо указать.

Спецификация модели на основе правил

[ редактировать ]

Ясно, что явное описание, в котором перечислены все возможные молекулярные виды (включая все их возможные состояния), все возможные реакции или переходы, которым могут подвергаться эти виды, а также все параметры, управляющие этими реакциями, очень быстро становится громоздким по мере сложности биологической системы. увеличивается. Поэтому разработчики моделей искали неявные , а не явные способы определения биологической сигнальной системы. Неявное описание — это описание, которое группирует реакции и параметры, применимые ко многим типам молекулярных частиц, в один шаблон реакции. Можно также добавить набор условий, которые управляют параметрами реакции, т. е. вероятностью или скоростью, с которой происходит реакция, или происходит ли она вообще. Явно упоминаются только те свойства молекулы или комплекса, которые имеют значение для данной реакции (влияющие на реакцию или на которые она влияет), а все остальные свойства игнорируются в описании реакции.

Например, скорость диссоциации лиганда от белка может зависеть от конформационного состояния белка, а не от его субклеточной локализации. Таким образом, неявное описание будет перечислять два процесса диссоциации (с разными скоростями, в зависимости от конформационного состояния), но будет игнорировать атрибуты, относящиеся к субклеточной локализации, поскольку они не влияют на скорость диссоциации лиганда и не зависят от нее. Это правило спецификации было кратко сформулировано как «Неважно, не пиши». [29]

Поскольку она написана не в терминах реакций, а в терминах более общих «правил реакций», охватывающих наборы реакций, этот вид спецификации часто называют «основанным на правилах» . [4] Такое описание системы с точки зрения модульных правил основано на предположении, что только подмножество функций или атрибутов имеет отношение к конкретному правилу реагирования. Если это предположение справедливо, набор реакций можно объединить в одно правило реакции. Такая грубая настройка сохраняет важные свойства основных реакций. Например, если реакции основаны на химической кинетике, то же самое можно сказать и о правилах, вытекающих из них.

Существует множество методов спецификации, основанных на правилах. В общем, спецификация модели — это отдельная задача от выполнения моделирования. Таким образом, среди существующих систем спецификации моделей, основанных на правилах, [4] некоторые концентрируются только на спецификации модели, позволяя пользователю затем экспортировать указанную модель в специальный механизм моделирования. Однако многие решения задачи спецификации содержат и способ интерпретации указанной модели. [3] Это делается путем предоставления метода моделирования модели или метода ее преобразования в форму, которую можно использовать для моделирования в других программах.

Ранним методом спецификации, основанным на правилах, является κ-исчисление. [1] алгебра процессов , которую можно использовать для кодирования макромолекул с их внутренними состояниями и местами связывания, а также для указания правил, по которым они взаимодействуют. [29] Целью κ-исчисления является создание языка для кодирования моделей с несколькими состояниями, а не интерпретация самих моделей. Симулятор, совместимый с Kappa, — KaSim. [33]

BioNetGen — это пакет программного обеспечения, который обеспечивает возможности как спецификации, так и моделирования. [2] [3] [4] [5] Модели, основанные на правилах, могут быть записаны с использованием определенного синтаксиса — языка BioNetGen (BNGL). [4] Основная концепция заключается в представлении биохимических систем в виде графов , где молекулы представлены в виде узлов (или наборов узлов), а химические связи — в виде ребер. Таким образом, правило реакции соответствует правилу переписывания графа. [3] BNGL предоставляет синтаксис для указания этих графиков и связанных с ними правил в виде структурированных строк. [4] Затем BioNetGen может использовать эти правила для создания обыкновенных дифференциальных уравнений (ОДУ) для описания каждой биохимической реакции. Альтернативно, он может генерировать список всех возможных видов и реакций в SBML . [34] [35] которые затем можно экспортировать в пакеты программного обеспечения для моделирования, которые могут читать SBML . Можно также использовать собственное программное обеспечение BioNetGen для моделирования на основе ODE и его способность генерировать реакции «на лету» во время стохастического моделирования. [5] Кроме того, модель, указанную в BNGL, может быть прочитана другим программным обеспечением для моделирования, например DYNSTOC. [12] ПравилоОбезьяна, [13] и НФСим. [14]

Еще один инструмент, который генерирует полные сети реакций на основе набора правил, — это компилятор аллостерических сетей (ANC). [6] Концептуально АНК рассматривает молекулы как аллостерические устройства с механизмом регуляции типа Монода-Ваймана-Чанге (MWC). [36] взаимодействия которых определяются их внутренним состоянием, а также внешними модификациями. Очень полезной особенностью АНК является то, что он автоматически вычисляет зависимые параметры, тем самым обеспечивая термодинамическую корректность. [37]

Расширение κ-исчисления обеспечивается React(C) . [38] Авторы React C показывают, что он может выражать стохастическое исчисление π. [39] Они также предоставляют алгоритм стохастического моделирования, основанный на стохастическом алгоритме Гиллеспи. [40] для моделей, указанных в React(C) . [38]

ML-правила [41] аналогичен React(C), но предоставляет дополнительную возможность вложенности: вид компонента модели со всеми его атрибутами может быть частью вида компонента более высокого порядка. Это позволяет правилам машинного обучения захватывать многоуровневые модели, которые могут устранить разрыв между, например, рядом биохимических процессов и макроскопическим поведением целой клетки или группы клеток. Например, экспериментальная модель деления клеток у делящихся дрожжей включает циклина / cdc2 связывание и активацию феромонов , секрецию и диффузию , деление клеток и движение клеток. [41] Модели, указанные в правилах ML, можно моделировать с помощью среды моделирования James II. [42] Подобный вложенный язык для представления многоуровневых биологических систем был предложен Ури и Плоткиным. [43] Формализм спецификации, основанный на структуре молекулярных конечных автоматов (MFA), может затем использоваться для генерации и моделирования системы ОДУ или для стохастического моделирования с использованием кинетического алгоритма Монте-Карло . [8]

Некоторые системы спецификаций, основанные на правилах, и связанные с ними инструменты создания сетей и моделирования были разработаны с учетом пространственной неоднородности, чтобы обеспечить реалистичное моделирование взаимодействий внутри биологических компартментов. Например, проект Simmune [44] [45] включает пространственный компонент: пользователи могут указывать свои многосостоятельные биомолекулы и взаимодействия внутри мембран или отсеков произвольной формы. Затем реакционный объем разделяется на взаимодействующие вокселы, и для каждого из этих субобъемов создается отдельная реакционная сеть.

Компилятор стохастического симулятора (SSC) [46] позволяет основанную на правилах модульную спецификацию взаимодействующих биомолекул в областях произвольно сложной геометрии. Опять же, система представлена ​​с помощью графов, в которых химические взаимодействия или явления диффузии формализованы как правила переписывания графов. [46] Затем компилятор генерирует всю сеть реакций перед запуском алгоритма стохастической реакции-диффузии.

использует другой подход PySB : [47] где спецификация модели встроена в язык программирования Python . Модель (или часть модели) представлена ​​в виде программы Python. Это позволяет пользователям сохранять биохимические процессы более высокого порядка, такие как катализ или полимеризация, в виде макросов и повторно использовать их по мере необходимости. Модели можно моделировать и анализировать с помощью библиотек Python, но модели PySB также можно экспортировать в BNGL. [4] каппа, [1] и СБМЛ. [34]

Модели, включающие многосостоятельные и многокомпонентные виды, также могут быть указаны на уровне 3 языка разметки системной биологии (SBML). [34] используя мультипакет. Имеется проект спецификации. [48]

Таким образом, учитывая только состояния и особенности, важные для конкретной реакции, спецификация модели на основе правил устраняет необходимость явного перечисления всех возможных молекулярных состояний, которые могут подвергаться аналогичной реакции, и тем самым обеспечивает эффективную спецификацию.

Проблема вычислений

[ редактировать ]

При запуске моделирования биологической модели любое программное обеспечение для моделирования оценивает набор правил, начиная с заданного набора начальных условий и обычно повторяя серию временных шагов до определенного времени окончания. Один из способов классифицировать алгоритмы моделирования — посмотреть на уровень анализа, на котором применяются правила: они могут быть популяционными, одночастичными или гибридными.

Оценка правил на основе населения

[ редактировать ]

При оценке правил на основе совокупности правила применяются к совокупностям. Все молекулы одного и того же вида в одном и том же состоянии собираются вместе. Применение определенного правила уменьшает или увеличивает размер одного из пулов, возможно, за счет другого.

Некоторые из наиболее известных классов подходов к моделированию в вычислительной биологии относятся к семейству популяционных, в том числе основанные на численном интегрировании обыкновенных уравнений и уравнений в частных производных и алгоритме стохастического моделирования Гиллеспи.

Дифференциальные уравнения описывают изменения молекулярных концентраций с течением времени детерминированным образом. Моделирование, основанное на дифференциальных уравнениях, обычно не пытается решить эти уравнения аналитически, а использует подходящий численный решатель .

Стохастический алгоритм Гиллеспи изменяет состав пулов молекул посредством развития случайных событий реакции, вероятность которых рассчитывается на основе скорости реакции и количества молекул в соответствии со стохастическим основным уравнением . [40]

В подходах, основанных на популяциях, можно думать о моделируемой системе как о находящейся в заданном состоянии в любой заданный момент времени, причем состояние определяется в соответствии с природой и размером населенных пулов молекул. Это означает, что пространство всех возможных состояний может стать очень большим. При использовании некоторых методов моделирования, реализующих численное интегрирование обыкновенных уравнений и уравнений в частных производных или стохастического алгоритма Гиллеспи, все возможные пулы молекул и реакции, в которых они проходят, определяются в начале моделирования, даже если они пусты. Такие методы «сначала сгенерировать» [4] плохо масштабируются с увеличением числа молекулярных состояний. [49] Например, недавно было подсчитано, что даже для простой модели CaMKII всего с 6 состояниями на субъединицу и 10 субъединицами потребуется 290 лет для создания всей реакционной сети на процессоре Intel Xeon с частотой 2,54 ГГц . [50] Кроме того, этап создания модели в методах «сначала генерировать» не обязательно завершается, например, когда модель включает сборку белков в комплексы произвольно большого размера, такие как актиновые нити. В этих случаях пользователь должен указать условие завершения. [3] [5]

Даже если можно успешно создать большую реакционную систему, ее моделирование с использованием оценки правил на основе совокупности может столкнуться с вычислительными ограничениями. В недавнем исследовании было показано, что мощный компьютер не способен моделировать белок с более чем 8 фосфорилирования . сайтами состояния фосфорилирования) с помощью обыкновенных дифференциальных уравнений. [14]

Предложены методы уменьшения размера пространства состояний. Один из них — рассматривать только состояния, соседние с текущим состоянием (т. е. состояния, которые могут быть достигнуты в течение следующей итерации) в каждый момент времени. Это избавляет от необходимости перечислять все возможные состояния в начале. Вместо этого реакции генерируются «на лету». [4] на каждой итерации. Эти методы доступны как для стохастических, так и для детерминированных алгоритмов. Эти методы по-прежнему основаны на определении (хотя и уменьшенной) реакционной сети - в отличие от «бессеточных» методов, обсуждаемых ниже.

Даже при генерировании сетей «на лету» сети, созданные для оценки правил на основе генеральной совокупности, могут стать довольно большими, и, следовательно, их будет сложно, а то и невозможно, обрабатывать вычислительно. Альтернативный подход обеспечивается оценкой правил на основе частиц.

Оценка правил на основе частиц

[ редактировать ]
Принципы моделирования на основе частиц. При моделировании на основе частиц каждая частица отслеживается индивидуально в процессе моделирования. В любой момент частица «видит» только те правила, которые к ней применяются. На этом рисунке показаны две молекулярные частицы (одна типа A выделена красным, другая типа B синего цвета) через три этапа гипотетического моделирования, следуя простому набору правил (приведенных справа). На каждом этапе правила, которые потенциально применимы к рассматриваемой частице, выделяются цветом этой частицы.

В моделировании на основе частиц (иногда называемом «агентным») белки, нуклеиновые кислоты, макромолекулярные комплексы или небольшие молекулы представлены как отдельные программные объекты , и их прогресс отслеживается на протяжении всего моделирования. [51] Поскольку оценка правил на основе частиц отслеживает отдельные частицы, а не популяции, она требует более высоких вычислительных затрат при моделировании систем с большим общим количеством частиц, но небольшим количеством типов (или пулов) частиц. [51] Однако в случаях комбинаторной сложности моделирование отдельных частиц является преимуществом, поскольку в любой момент моделирования необходимо учитывать только существующие молекулы, их состояния и реакции, в которых они могут проходить. Оценка правил на основе частиц не требует создания полных или частичных сетей реакций в начале моделирования или в любой другой точке моделирования и поэтому называется «бессетевой».

Этот метод снижает сложность модели на этапе моделирования и тем самым экономит время и вычислительные мощности. [9] [10] Моделирование следует за каждой частицей, и на каждом этапе моделирования частица «видит» только те реакции (или правила), которые к ней применяются. Это зависит от состояния частицы и, в некоторой реализации, от состояний ее соседей по голоферменту или комплексу. По мере продолжения моделирования состояния частиц обновляются в соответствии с запущенными правилами. [10]

Некоторые пакеты моделирования на основе частиц используют специальный формализм для спецификации реагентов, параметров и правил. Другие могут читать файлы в признанном формате спецификации на основе правил, например BNGL. [4]

Непространственные методы, основанные на частицах

[ редактировать ]

СточСим [11] симулятор на основе частиц, представляет собой стохастический используемый в основном для моделирования химических реакций и других молекулярных переходов. Алгоритм, используемый в StochSim, отличается от более широко известного стохастического алгоритма Гиллеспи. [40] в том смысле, что он работает с отдельными объектами, а не с пулами объектов, что делает его основанным на частицах, а не на популяциях.

В StochSim каждый вид молекул может быть снабжен рядом флагов двоичного состояния , представляющих определенную модификацию. Реакции можно сделать зависимыми от набора флагов состояния, которым присвоены определенные значения. Кроме того, результат реакции может включать изменение государственного флага. При этом сущности могут быть расположены в геометрические массивы (например, для голоферментов, состоящих из нескольких субъединиц), а реакции могут быть «соседно-чувствительными», т.е. на вероятность реакции для данного объекта влияет значение флага состояния. на соседнем объекте. Эти свойства делают StochSim идеально подходящим для моделирования молекул с несколькими состояниями, организованных в голоферменты или комплексы заданного размера. Действительно, StochSim использовался для моделирования кластеров бактериальных хемотаксических рецепторов. [52] и холоферменты CaMKII. [28]

Расширение StochSim включает симулятор DYNSTOC на основе частиц, который использует алгоритм, подобный StochSim, для моделирования моделей, заданных на языке BioNetGen (BNGL). [4] и улучшает обращение с молекулами внутри макромолекулярных комплексов . [12]

Еще один стохастический симулятор на основе частиц, который может читать входные файлы BNGL, — это RuleMonkey. [13] Алгоритм моделирования [9] отличается от алгоритмов, лежащих в основе StochSim и DYNSTOC, тем, что временной шаг моделирования является переменным.

Бессетевой стохастический симулятор (NFSim) отличается от описанных выше тем, что позволяет определять скорости реакции как произвольные математические или условные выражения и тем самым облегчает выборочное уточнение моделей. [14] RuleMonkey и NFsim реализуют разные, но связанные алгоритмы моделирования. Подробный обзор и сравнение обоих инструментов дали Ян и Главачек. [53]

Легко представить себе биологическую систему, в которой некоторые компоненты представляют собой сложные многосостоятельные молекулы, тогда как другие имеют мало возможных состояний (или даже одно) и существуют в большом количестве. Для моделирования таких систем был предложен гибридный подход: в рамках гибридной системы частиц/популяций (HPP) пользователь может указать модель, основанную на правилах, но может обозначить некоторые виды, которые в дальнейшем будут рассматриваться как популяции (а не как частицы). моделирование. [10] Этот метод сочетает в себе вычислительные преимущества моделирования на основе частиц для многосостоятельных систем с относительно низким числом молекул и популяционного моделирования для систем с большим числом молекул и небольшим числом возможных состояний. Спецификация моделей HPP поддерживается BioNetGen, [4] и моделирование может быть выполнено с помощью NFSim. [14]

Пространственные методы на основе частиц

[ редактировать ]
Снимок экрана моделирования MCell передачи сигналов кальция в позвоночнике. Хотя в моделирование были включены и другие типы молекул, регулируемых кальцием, визуализируются только молекулы CaMKII. Они показаны красным, когда они связаны с кальмодулином, и черным, когда они не связаны. Отделение моделирования представляет собой реконструкцию дендритного позвоночника . [54] Область постсинаптической плотности показана красным, голова и шея шипа - серым, а родительский дендрит - желтым. Рисунок был создан путем визуализации результатов моделирования в Blender .

Методы, основанные на пространственных частицах, отличаются от описанных выше методов явным представлением пространства.

Одним из примеров симулятора на основе частиц, который позволяет отображать клеточные компартменты, является SRSim. [17] [18] SRSim интегрирован в симулятор молекулярной динамики LAMMPS. [55] и позволяет пользователю указать модель в BNGL. [4] SRSim позволяет пользователям указывать геометрию частиц при моделировании, а также места взаимодействия. Поэтому он особенно хорош для моделирования сборки и структуры сложных биомолекулярных комплексов, о чем свидетельствует недавняя модель внутреннего кинетохора . [56]

MCell [19] [20] [21] позволяет отслеживать отдельные молекулы в произвольно сложных геометрических средах, определяемых пользователем. Это позволяет моделировать биомолекулы в реалистичных реконструкциях живых клеток, включая клетки со сложной геометрией, например, нейронов . Реакционное отделение представляет собой реконструкцию дендритного шипа. [54]

MCell использует специальный формализм внутри самого MCell для определения модели с несколькими состояниями: в MCell можно назначать «слоты» любым молекулярным видам . Каждый слот соответствует определенной модификации, и молекуле может быть присвоено любое количество слотов. Каждый слот может быть занят определенным состоянием. Государства не обязательно являются бинарными. Например, слот, описывающий связывание конкретного лиганда с интересующим белком, может принимать состояния «несвязанный», «частично связанный» и «полностью связанный».

Синтаксис слотов и состояний в MCell также можно использовать для моделирования мультимерных белков или макромолекулярных комплексов. При таком использовании слот является заполнителем для субъединицы или молекулярного компонента комплекса , а состояние слота будет указывать, отсутствует или присутствует конкретный белковый компонент в комплексе. Об этом можно подумать, что макромолекулы MCell могут иметь несколько измерений : «измерение состояния» и одно или несколько «пространственных измерений». «Измерение состояния» используется для описания множества возможных состояний, составляющих белок с несколькими состояниями, тогда как пространственное измерение(я) описывает топологические отношения между соседними субъединицами или членами макромолекулярного комплекса. Одним из недостатков этого метода представления белковых комплексов по сравнению с Meredys является то, что MCell не допускает диффузии комплексов и, следовательно, молекул с несколькими состояниями. В некоторых случаях этого можно обойти, регулируя константы диффузии лигандов, которые взаимодействуют с комплексом, используя функции контрольных точек или комбинируя моделирование на разных уровнях.

Примеры моделей нескольких состояний в биологии

[ редактировать ]

(Далеко не исчерпывающий) выбор моделей биологических систем, включающих многосостоятельные молекулы и использующих некоторые из обсуждаемых здесь инструментов, приведен в таблице ниже.

Примеры многогосударственных моделей биологических систем
Биологическая система Спецификация Вычисление Ссылка
Сигнальный путь бактериального хемотаксиса СточСим СточСим [57]
регулирование CaMKII СточСим СточСим [28]
ERBB Передача сигналов рецептора БиоНетГен НФСим [30]
Эукариотические синтетические генные цепи БиоНетГен, ПРОМОТ [58] КОПАСИ [59] [31]
Передача сигналов РНК Каппа КаSим [60]
Кооперативность аллостерических белков Компилятор аллостерических сетей (ANC) МАТЛАБ [6]
Хемосенсивирование в Dictyostelium Симмун Симмун [44]
Т-клеточных рецепторов Активация ССК ССК [61]
Митотический кинетохор человека БиоНетГен СРСим [62]
Клеточный цикл делящихся дрожжей ML-правила ДЖЕЙМС II [42] [41]

См. также

[ редактировать ]

Ссылки

[ редактировать ]

Эта статья была адаптирована из следующего источника под лицензией CC BY 4.0 ( 2014 г. ) ( отчеты рецензента ): Мелани и Стефан; Томас М. Бартол; Терренс Дж. Сейновски ; Мэри Б. Кеннеди (сентябрь 2014 г.). «Многосостояние моделирования биомолекул» . PLOS Вычислительная биология . 10 (9): e1003844. doi : 10.1371/JOURNAL.PCBI.1003844 . ISSN   1553-734X . ПМК   4201162 . ПМИД   25254957 . Викиданные   Q18145441 .

  1. ^ Перейти обратно: а б с Данос В., Ланеве С. (2004). «Формальная молекулярная биология» . Теоретическая информатика . 325 : 69–110. дои : 10.1016/j.tcs.2004.03.065 .
  2. ^ Перейти обратно: а б Блинов М.Л., Федер Дж.Р., Гольдштейн Б., Главачек В.С. (ноябрь 2004 г.). «BioNetGen: программное обеспечение для моделирования передачи сигналов на основе правил на основе взаимодействия молекулярных доменов» . Биоинформатика . 20 (17): 3289–91. doi : 10.1093/биоинформатика/bth378 . ПМИД   15217809 .
  3. ^ Перейти обратно: а б с д и Федер-младший, Блинов М.Л., Гольдштейн Б., Главачек В.С. (2005). «Моделирование биохимических сетей на основе правил». Сложность . 10 (4): 22–41. Бибкод : 2005Cmplx..10d..22F . дои : 10.1002/cplx.20074 . S2CID   9307441 .
  4. ^ Перейти обратно: а б с д и ж г час я дж к л м Главачек В.С., Фаедер Дж.Р., Блинов М.Л., Познер Р.Г., Хука М., Фонтана В. (июль 2006 г.). «Правила моделирования систем передачи сигналов». СТКЭ науки . 2006 (344): re6. CiteSeerX   10.1.1.83.1561 . дои : 10.1126/stke.3442006re6 . ПМИД   16849649 . S2CID   1816082 .
  5. ^ Перейти обратно: а б с д Фаедер-младший, Блинов М.Л., Главачек В.С. (2009). «Моделирование биохимических систем на основе правил с помощью BioNetGen». Системная биология . Методы молекулярной биологии. Том. 500. Тотова, Нью-Джерси: Humana Press. стр. 113–67. CiteSeerX   10.1.1.323.9577 . дои : 10.1007/978-1-59745-525-1_5 . ISBN  978-1-934115-64-0 . ПМИД   19399430 .
  6. ^ Перейти обратно: а б с Оливье Дж. Ф., Шахрезаи В., Суэйн П. С. (ноябрь 2010 г.). «Масштабируемое моделирование аллостерических белков и биохимических сетей на основе правил» . PLOS Вычислительная биология . 6 (11): e1000975. Бибкод : 2010PLSCB...6E0975O . дои : 10.1371/journal.pcbi.1000975 . ПМЦ   2973810 . ПМИД   21079669 .
  7. ^ Лок Л., Брент Р. (январь 2005 г.). «Автоматическое создание клеточных реакционных сетей с помощью Moleculizer 1.0». Природная биотехнология . 23 (1): 131–6. дои : 10.1038/nbt1054 . ПМИД   15637632 . S2CID   23696958 .
  8. ^ Перейти обратно: а б Ян Дж., Мэн Х., Главачек В.С. (ноябрь 2010 г.). «Моделирование на основе правил и симуляция биохимических систем с помощью молекулярных конечных автоматов» . ИЭПП Системная биология . 4 (6): 453–66. arXiv : 1007.1315 . дои : 10.1049/iet-syb.2010.0015 . ПМК   3070173 . ПМИД   21073243 .
  9. ^ Перейти обратно: а б с д Ян Дж., Монин М.И., Фаедер-младший, Главачек В.С. (сентябрь 2008 г.). «Кинетический метод Монте-Карло для моделирования биохимических сетей на основе правил» . Физический обзор E . 78 (3, часть 1): 031910. arXiv : 0712.3773 . Бибкод : 2008PhRvE..78c1910Y . дои : 10.1103/PhysRevE.78.031910 . ПМК   2652652 . ПМИД   18851068 .
  10. ^ Перейти обратно: а б с д Хогг, Дж.С., Харрис, Л.А., Стовер, Л.Дж., Наир, Н.С., и Фейдер, младший (2013). Точное гибридное моделирование частиц и популяций основанных на правилах моделей биохимических систем. Препринт arXiv arXiv:1301.6854.
  11. ^ Перейти обратно: а б Ле Новер Н., Симидзу Т.С. (июнь 2001 г.). «STOCHSIM: моделирование стохастических биомолекулярных процессов» . Биоинформатика . 17 (6): 575–6. дои : 10.1093/биоинформатика/17.6.575 . ПМИД   11395441 .
  12. ^ Перейти обратно: а б с Колвин Дж., Монин М.И., Федер Дж.Р., Главачек В.С., Фон Хофф Д.Д., Познер Р.Г. (апрель 2009 г.). «Моделирование крупномасштабных моделей, основанных на правилах» . Биоинформатика . 25 (7): 910–7. doi : 10.1093/биоинформатика/btp066 . ПМК   2660871 . ПМИД   19213740 .
  13. ^ Перейти обратно: а б с Колвин Дж., Монин М.И., Гутенкунст Р.Н., Главачек В.С., Фон Хофф Д.Д., Познер Р.Г. (июль 2010 г.). «RuleMonkey: программное обеспечение для стохастического моделирования моделей, основанных на правилах» . БМК Биоинформатика . 11 : 404. дои : 10.1186/1471-2105-11-404 . ПМЦ   2921409 . ПМИД   20673321 .
  14. ^ Перейти обратно: а б с д и Снеддон М.В., Фейдер-младший, Эмонет Т. (февраль 2011 г.). «Эффективное моделирование, симуляция и грубая обработка биологической сложности с помощью NFsim». Природные методы . 8 (2): 177–83. дои : 10.1038/nmeth.1546 . ПМИД   21186362 . S2CID   5412795 .
  15. ^ Шенеберг Дж., Ульрих А., Ноэ Ф. (24 октября 2014 г.). «Инструменты моделирования динамики реакции-диффузии частиц в непрерывном пространстве» . БМК Биофизика . 7 (1): 11. дои : 10.1186/s13628-014-0011-5 . ПМЦ   4347613 . ПМИД   25737778 .
  16. ^ Толле Д.П., Ле Новер Н. (март 2010 г.). «Meredys, многокамерный симулятор реакции-диффузии, использующий многосоставные реалистичные молекулярные комплексы» . Системная биология BMC . 4:24 . дои : 10.1186/1752-0509-4-24 . ПМЦ   2848630 . ПМИД   20233406 .
  17. ^ Перейти обратно: а б Грюнерт Г., Ибрагим Б., Ленсер Т., Лохель М., Хинце Т., Диттрих П. (июнь 2010 г.). «Пространственное моделирование на основе правил с диффундирующими геометрически ограниченными молекулами» . БМК Биоинформатика . 11 : 307. дои : 10.1186/1471-2105-11-307 . ПМЦ   2911456 . ПМИД   20529264 .
  18. ^ Перейти обратно: а б Грюнерт Г., Диттрих П. (2011). «Использование программного обеспечения SRSim для пространственного и основанного на правилах моделирования комбинаторно сложных систем биохимических реакций». Мембранные вычисления . Конспекты лекций по информатике. Том. 6501. стр. 240–256. дои : 10.1007/978-3-642-18123-8_19 . ISBN  978-3-642-18122-1 .
  19. ^ Перейти обратно: а б Стайлз-младший, Ван Хелден Д., Бартол Т.М., Солпитер Э.Э., Солпитер М.М. (июнь 1996 г.). «Миниатюрное время нарастания тока концевой пластинки менее 100 микросекунд в результате улучшенной двойной записи можно смоделировать с помощью пассивной диффузии ацетилхолина из синаптического пузырька» . Труды Национальной академии наук Соединенных Штатов Америки . 93 (12): 5747–52. Бибкод : 1996PNAS...93.5747S . дои : 10.1073/pnas.93.12.5747 . ПМК   39132 . ПМИД   8650164 .
  20. ^ Перейти обратно: а б Стайлз-младший, Бартол ТМ (2001). Вычислительная нейронаука: реалистичное моделирование для экспериментаторов. В: Де Шуттер, Э (ред.). Вычислительная нейронаука: реалистичное моделирование для экспериментаторов. CRC Press, Бока-Ратон.
  21. ^ Перейти обратно: а б Керр Р.А., Бартол Т.М., Каминский Б., Диттрих М., Чанг Дж.К., Баден С.Б. и др. (октябрь 2008 г.). «Методы быстрого моделирования Монте-Карло биологических реакционно-диффузионных систем в растворе и на поверхностях» . Журнал SIAM по научным вычислениям . 30 (6): 3126–3149. Бибкод : 2008ГАО...30.3126К . дои : 10.1137/070692017 . ПМК   2819163 . ПМИД   20151023 .
  22. ^ Перейти обратно: а б Брей Д. (июль 1995 г.). «Белковые молекулы как вычислительные элементы в живых клетках». Природа . 376 (6538): 307–12. Бибкод : 1995Natur.376..307B . дои : 10.1038/376307a0 . ПМИД   7630396 . S2CID   4326068 .
  23. ^ Перейти обратно: а б Энди Д., Брент Р. (январь 2001 г.). «Моделирование клеточного поведения» . Природа . 409 (6818): 391–5. Бибкод : 2001Natur.409..391E . дои : 10.1038/35053181 . ПМИД   11201753 . S2CID   480515 .
  24. ^ Перейти обратно: а б Брей Д. (февраль 2003 г.). «Геномика. Молекулярная расточительность». Наука . 299 (5610): 1189–90. дои : 10.1126/science.1080010 . ПМИД   12595679 . S2CID   34035288 .
  25. ^ Перейти обратно: а б Главачек В.С., Федер Дж.Р., Блинов М.Л., Перельсон А.С., Гольдштейн Б. (декабрь 2003 г.). «Сложность комплексов в передаче сигналов» . Биотехнология и биоинженерия . 84 (7): 783–94. дои : 10.1002/бит.10842 . ПМИД   14708119 . S2CID   9092264 .
  26. ^ Беннетт М.К., Эронду Н.Е., Кеннеди М.Б. (октябрь 1983 г.). «Очистка и характеристика кальмодулинзависимой протеинкиназы, концентрация которой высока в головном мозге» . Журнал биологической химии . 258 (20): 12735–44. дои : 10.1016/S0021-9258(17)44239-6 . ПМИД   6313675 .
  27. ^ Розенберг О.С., Дейндл С., Сунг Р.Дж., Нэрн А.С., Куриян Дж. (декабрь 2005 г.). «Структура аутоингибированного киназного домена CaMKII и SAXS-анализ голофермента» . Клетка . 123 (5): 849–60. дои : 10.1016/j.cell.2005.10.029 . ПМИД   16325579 . S2CID   2654357 .
  28. ^ Перейти обратно: а б с Стефан М.И., Маршалл Д.П., Ле Новер Н. (2012). «Структурный анализ и стохастическое моделирование позволяют предположить механизм захвата кальмодулина CaMKII» . ПЛОС ОДИН . 7 (1): e29406. Бибкод : 2012PLoSO...729406S . дои : 10.1371/journal.pone.0029406 . ПМК   3261145 . ПМИД   22279535 .
  29. ^ Перейти обратно: а б с Данос В., Ферет Дж., Фонтана В., Хармер Р., Кривин Дж. (2007). Моделирование сотовой сигнализации на основе правил. Материалы восемнадцатой международной конференции по теории параллелизма, CONCUR 2007, Лиссабон, Португалия.
  30. ^ Перейти обратно: а б Кример М.С., Стайтс Э.К., Азиз М., Кэхилл Дж.А., Тан К.В., Беренс М.Е. и др. (август 2012 г.). «Спецификация, аннотация, визуализация и моделирование большой основанной на правилах модели передачи сигналов рецептора ERBB» . Системная биология BMC . 6 : 107. дои : 10.1186/1752-0509-6-107 . ПМЦ   3485121 . ПМИД   22913808 .
  31. ^ Перейти обратно: а б Маркизио М.А., Колаяково М., Уайтхед Э., Стеллинг Дж. (май 2013 г.). «Модульное моделирование на основе правил для разработки цепей синтетических генов эукариот» . Системная биология BMC . 7:42 . дои : 10.1186/1752-0509-7-42 . ПМК   3680069 . ПМИД   23705868 .
  32. ^ Чилек Л.А., Стайтс ЕС, Познер Р.Г., Главачек В.С. (2013)Инновации в подходе к моделированию на основе правил. В системной биологии: интегративная биология и инструменты моделирования, том 1 (Прокоп А, Чукас Б, редакторы), Springer.
  33. ^ Ферет Дж., Данос В., Кривин Дж., Хармер Р., Фонтана В. (апрель 2009 г.). «Внутреннее укрупнение молекулярных систем» . Труды Национальной академии наук Соединенных Штатов Америки . 106 (16): 6453–8. Бибкод : 2009PNAS..106.6453F . дои : 10.1073/pnas.0809908106 . ПМЦ   2672529 . ПМИД   19346467 .
  34. ^ Перейти обратно: а б с Хука М., Финни А., Сауро Х.М., Болури Х., Дойл Дж.К., Китано Х. и др. (март 2003 г.). «Язык разметки системной биологии (SBML): среда для представления и обмена моделями биохимических сетей» . Биоинформатика . 19 (4): 524–31. doi : 10.1093/биоинформатика/btg015 . ПМИД   12611808 .
  35. ^ Финни А., Хука М. (декабрь 2003 г.). «Язык разметки системной биологии: уровень 2 и выше». Труды Биохимического общества . 31 (Часть 6): 1472–3. CiteSeerX   10.1.1.466.8001 . дои : 10.1042/bst0311472 . ПМИД   14641091 .
  36. ^ Моно Дж., Вайман Дж., Чанже Дж. П. (май 1965 г.). «О природе аллостерических переходов: правдоподобная модель». Журнал молекулярной биологии . 12 : 88–118. дои : 10.1016/S0022-2836(65)80285-6 . ПМИД   14343300 .
  37. ^ Колкухун Д., Доусленд К.А., Беато М., Плестед А.Дж. (июнь 2004 г.). «Как обеспечить микроскопическую обратимость в сложных механизмах реакций» . Биофизический журнал . 86 (6): 3510–8. Бибкод : 2004BpJ....86.3510C . дои : 10.1529/biophysj.103.038679 . ПМК   1304255 . ПМИД   15189850 .
  38. ^ Перейти обратно: а б Джон М., Луссейн К., Нирен Дж. и Версари К. (2011). Правила биохимических реакций с ограничениями. В языках и системах программирования (стр. 338-357). Шпрингер Берлин Гейдельберг.
  39. ^ Приами С (1995). «Стохастическое π-исчисление» . Компьютерный журнал . 38 (7): 578–589. дои : 10.1093/comjnl/38.7.578 .
  40. ^ Перейти обратно: а б с Гиллеспи Д.Т. (1977). «Точное стохастическое моделирование связанных химических реакций». J Phys Chem . 81 (25): 2340–2361. CiteSeerX   10.1.1.704.7634 . дои : 10.1021/j100540a008 . S2CID   2606191 .
  41. ^ Перейти обратно: а б с Маус С., Рыбацкий С., Урмахер А.М. (октябрь 2011 г.). «Многоуровневое моделирование клеточных биологических систем на основе правил» . Системная биология BMC . 5 : 166. дои : 10.1186/1752-0509-5-166 . ПМК   3306009 . ПМИД   22005019 .
  42. ^ Перейти обратно: а б Дж. Химмельспах и А. М. Урмахер, «Подключи и моделируй», Труды 40-го ежегодного симпозиума по моделированию. Компьютерное общество IEEE, 2007, стр. 137–143.
  43. ^ Оури Н., Плоткин Г. (2013). «Многоуровневое моделирование посредством стохастического многоуровневого переписывания мультимножеств» (PDF) . Математические структуры в информатике . 23 (2): 471–503. дои : 10.1017/s0960129512000199 . hdl : 20.500.11820/2c05ac75-14eb-4939-bf71-5e76b9a942ef . S2CID   702281 .
  44. ^ Перейти обратно: а б Мейер-Шеллерсхайм М, Сюй X, Ангерманн Б, Кункель Э.Дж., Джин Т., Жермен Р.Н. (июль 2006 г.). «Ключевая роль локальной регуляции в хемосенсорстве выявлена ​​с помощью нового метода моделирования, основанного на молекулярном взаимодействии» . PLOS Вычислительная биология . 2 (7): е82. Бибкод : 2006PLSCB...2...82M . дои : 10.1371/journal.pcbi.0020082 . ПМЦ   1513273 . ПМИД   16854213 .
  45. ^ Ангерманн Б.Р., Клаушен Ф., Гарсия А.Д., Прустель Т., Чжан Ф., Жермен Р.Н., Мейер-Шеллерсхайм М. (январь 2012 г.). «Вычислительное моделирование процессов клеточной сигнализации, встроенных в динамические пространственные контексты» . Природные методы . 9 (3): 283–9. дои : 10.1038/nmeth.1861 . ПМЦ   3448286 . ПМИД   22286385 .
  46. ^ Перейти обратно: а б Лис М., Артёмов М.Н., Девадас С., Чакраборти А.К. (сентябрь 2009 г.). «Эффективное стохастическое моделирование реакционно-диффузионных процессов методом прямой компиляции» . Биоинформатика . 25 (17): 2289–91. doi : 10.1093/биоинформатика/btp387 . ПМЦ   2734316 . ПМИД   19578038 .
  47. ^ Лопес К.Ф., Мюлих Дж.Л., Бахман Дж.А., Зоргер П.К. (2013). «Программирование биологических моделей на Python с использованием PySB» . Молекулярная системная биология . 9 : 646. дои : 10.1038/msb.2013.1 . ПМЦ   3588907 . ПМИД   23423320 .
  48. ^ Чжан Ф, Мейер-Шеллерсхайм М (2013). «Спецификация пакета SBML уровня 3: пакет видов с несколькими состояниями, многокомпонентными и многокамерными видами для SBML уровня 3 (Multi). Версия 1, выпуск 01 (проект, ред. 369)» .
  49. ^ Толле Д.П., Ле Новер Н. (2006). «Стохастическое моделирование на основе частиц в системной биологии». Курс. Биоинформ . 1 (3): 315–320. дои : 10.2174/157489306777827964 . S2CID   41366617 .
  50. ^ Михальски П.Дж., Лоев Л.М. (июнь 2012 г.). «Активация и динамика CaMKII не зависят от структуры голофермента: приближение голофермента с бесконечными субъединицами» . Физическая биология . 9 (3): 036010. Бибкод : 2012PhBio...9c6010M . дои : 10.1088/1478-3975/9/3/036010 . ПМК   3507550 . ПМИД   22683827 .
  51. ^ Перейти обратно: а б Могилнер А. , Аллард Дж., Уоллман Р. (апрель 2012 г.). «Полярность клетки: количественное моделирование как инструмент клеточной биологии». Наука . 336 (6078): 175–9. Бибкод : 2012Sci...336..175M . дои : 10.1126/science.1216380 . ПМИД   22499937 . S2CID   10491696 .
  52. ^ Левин, доктор медицинских наук, Симидзу Т.С., Брей Д. (апрель 2002 г.). «Связывание и диффузия молекул CheR внутри кластера мембранных рецепторов» . Биофизический журнал . 82 (4): 1809–17. Бибкод : 2002BpJ....82.1809L . дои : 10.1016/S0006-3495(02)75531-8 . ПМК   1301978 . ПМИД   11916840 .
  53. ^ Ян Дж., Главачек В.С. (октябрь 2011 г.). «Эффективность отбора проб реагентов при бессетевом моделировании моделей биохимических систем, основанных на правилах» . Физическая биология . 8 (5): 055009. Бибкод : 2011PhBio...8e5009Y . дои : 10.1088/1478-3975/8/5/055009 . ПМК   3168694 . ПМИД   21832806 .
  54. ^ Перейти обратно: а б Кинни Дж.П., Спейсек Дж., Бартол Т.М., Баджадж К.Л., Харрис К.М., Сейновски Т.Дж. (февраль 2013 г.). «Внеклеточные листы и туннели модулируют диффузию глутамата в нейропиле гиппокампа» . Журнал сравнительной неврологии . 521 (2): 448–64. дои : 10.1002/cne.23181 . ПМК   3540825 . ПМИД   22740128 .
  55. ^ Плимптон С (март 1995 г.). «Быстрые параллельные алгоритмы ближней молекулярной динамики» . Журнал вычислительной физики . 117 (1): 1–9. Бибкод : 1995JCoPh.117....1P . дои : 10.1006/jcph.1995.1039 . S2CID   15881414 .
  56. ^ Чернышков С., Херда С., Грюнерт Г., Дёринг В., Герлих Д., Хофмайстер А. и др. (сентябрь 2013 г.). «Моделирование на основе правил и моделирование внутренней структуры кинетохор». Прогресс биофизики и молекулярной биологии . 113 (1): 33–45. doi : 10.1016/j.pbiomolbio.2013.03.010 . ПМИД   23562479 .
  57. ^ Симидзу Т.С., Аксенов С.В., Брэй Д. (май 2003 г.). «Пространственно расширенная стохастическая модель сигнального пути бактериального хемотаксиса». Журнал молекулярной биологии . 329 (2): 291–309. дои : 10.1016/s0022-2836(03)00437-6 . ПМИД   12758077 .
  58. ^ Миршель С., Стейнмец К., Ремпель М., Гинкель М., Жиль Э.Д. (март 2009 г.). «ПРОМОТ: модульное моделирование для системной биологии» . Биоинформатика . 25 (5): 687–9. doi : 10.1093/биоинформатика/btp029 . ПМЦ   2647835 . ПМИД   19147665 .
  59. ^ Хупс С., Сале С., Гауджес Р., Ли С., Пале Дж., Симус Н. и др. (декабрь 2006 г.). «COPASI — симулятор сложного пути» . Биоинформатика . 22 (24): 3067–74. doi : 10.1093/биоинформатика/btl485 . ПМИД   17032683 .
  60. ^ Эйткен С., Александр Р.Д., Беггс Дж.Д. (сентябрь 2013 г.). «Кинетическая модель фосфорилирования С-концевого домена РНК-полимеразы II на основе правил» . Журнал Королевского общества, Интерфейс . 10 (86): 20130438. doi : 10.1098/rsif.2013.0438 . ПМЦ   3730697 . ПМИД   23804443 .
  61. ^ Артёмов М.Н., Лис М., Девадас С., Дэвис М.М., Чакраборти А.К. (сентябрь 2010 г.). «Связывание CD4 и CD8 с молекулами MHC в первую очередь способствует усилению доставки Lck» . Труды Национальной академии наук Соединенных Штатов Америки . 107 (39): 16916–21. Бибкод : 2010PNAS..10716916A . дои : 10.1073/pnas.1010568107 . ПМЦ   2947881 . ПМИД   20837541 .
  62. ^ Ибрагим Б., Хенце Р., Грюнерт Г., Эгберт М., Хувальд Дж., Диттрих П. (июль 2013 г.). «Пространственное моделирование на основе правил: метод и его применение к митотической кинетохоре человека» . Клетки . 2 (3): 506–44. дои : 10.3390/cells2030506 . ПМЦ   3972674 . ПМИД   24709796 .
Retrieved from "https://en.wikipedia.org/w/index.php?title=Multi-state_modeling_of_biomolecules&oldid=1225411404"
Arc.Ask3.Ru: конец переведенного документа.
Arc.Ask3.Ru
Номер скриншота №: b6e784041eeb4e9258775bc653487e9e__1716529020
URL1:https://arc.ask3.ru/arc/aa/b6/9e/b6e784041eeb4e9258775bc653487e9e.html
Заголовок, (Title) документа по адресу, URL1:
Multi-state modeling of biomolecules - Wikipedia
Данный printscreen веб страницы (снимок веб страницы, скриншот веб страницы), визуально-программная копия документа расположенного по адресу URL1 и сохраненная в файл, имеет: квалифицированную, усовершенствованную (подтверждены: метки времени, валидность сертификата), открепленную ЭЦП (приложена к данному файлу), что может быть использовано для подтверждения содержания и факта существования документа в этот момент времени. Права на данный скриншот принадлежат администрации Ask3.ru, использование в качестве доказательства только с письменного разрешения правообладателя скриншота. Администрация Ask3.ru не несет ответственности за информацию размещенную на данном скриншоте. Права на прочие зарегистрированные элементы любого права, изображенные на снимках принадлежат их владельцам. Качество перевода предоставляется как есть. Любые претензии, иски не могут быть предъявлены. Если вы не согласны с любым пунктом перечисленным выше, вы не можете использовать данный сайт и информация размещенную на нем (сайте/странице), немедленно покиньте данный сайт. В случае нарушения любого пункта перечисленного выше, штраф 55! (Пятьдесят пять факториал, Денежную единицу (имеющую самостоятельную стоимость) можете выбрать самостоятельно, выплаичвается товарами в течение 7 дней с момента нарушения.)