Вращение

Эта статья о движении физического тела. Чтобы узнать о других значениях, см. Вращение (значения) .

«Поворот» перенаправляется сюда. Чтобы узнать о песне, см. «Поворот (песня)» . Чтобы узнать о городе-призраке, см. Ротэйт, Канзас .

Сфера, вращающаяся (вращающаяся) вокруг оси.

Вращение или вращательное движение — это круговое движение объекта вокруг центральной линии, известной как ось вращения . Плоская фигура может вращаться как по часовой стрелке, так и против часовой стрелки вокруг перпендикулярной оси, пересекающейся в любом месте внутри или снаружи фигуры в центре вращения . Твердая фигура имеет бесконечное количество возможных осей и углов поворота , включая хаотическое вращение (между произвольными ориентациями ), в отличие от вращения вокруг неподвижной оси .

Частный случай вращения с внутренней осью, проходящей через собственный центр масс тела , известен как вращение (или авторотация ). В этом случае поверхность пересечения внутренней оси вращения можно назвать полюсом ; например, вращение Земли определяет географические полюса . Вращение вокруг оси, полностью внешней по отношению к движущемуся телу, называется вращением (или орбитой ), например, орбита Земли вокруг Солнца . Концы внешней оси вращения можно назвать полюсами орбиты .

Каждый тип вращения связан с соответствующим типом угловой скорости (угловая скорость вращения и орбитальная угловая скорость) и углового момента (угловой момент вращения и орбитальный угловой момент).

Математика

Основная статья: Вращение (математика)

Вращение ( угловое смещение ) плоской фигуры вокруг точки

Вращательная орбита v спин

Связь между осью вращения, плоскостью орбиты и осевым наклоном (для Земли)

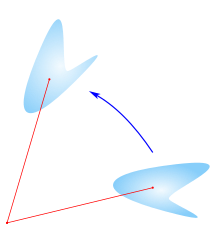
Математически вращение — это движение твердого тела , которое, в отличие от перемещения , удерживает хотя бы одну точку неподвижной. Это определение применимо к вращениям в двух измерениях (в плоскости), при которых ровно одна точка остается неподвижной; а также в трех измерениях (в пространстве), в которых дополнительные точки могут оставаться фиксированными (например, при вращении вокруг фиксированной оси, как бесконечная линия).

Все движения твердого тела представляют собой вращения, перемещения или их комбинации.

Вращение — это просто прогрессивная радиальная ориентация к общей точке. Эта общая точка лежит внутри оси этого движения. Ось перпендикулярна плоскости движения.

Если за вращением вокруг точки или оси следует второе вращение вокруг той же точки/оси, происходит третье вращение. Обратное . ( инверсное ) вращение также является вращением Таким образом, вращения вокруг точки/оси образуют группу . Однако вращение вокруг точки или оси и вращение вокруг другой точки/оси может привести к чему-то иному, чем вращение, например, к перемещению.

Вращения вокруг осей x , y и z называются главными вращениями . Вращение вокруг любой оси можно выполнить, выполнив вращение вокруг оси x , за которым следует вращение вокруг оси y , а затем вращение вокруг оси z . Другими словами, любое пространственное вращение можно разложить на комбинацию основных вращений.

См. также: ротор (математика) , циклическая перестановка , углы Эйлера , твердое тело , вращение вокруг фиксированной оси , группа вращения SO(3) , матрица вращения , угол оси , кватернион и изометрия.

Фиксированная ось и фиксированная точка

Комбинация любой последовательности вращений объекта в трех измерениях вокруг фиксированной точки всегда эквивалентна вращению вокруг оси (которое можно рассматривать как вращение в плоскости, перпендикулярной этой оси). Аналогично, скорость вращения объекта в трёх измерениях в любой момент времени вращается вокруг некоторой оси, хотя эта ось может меняться с течением времени.

В других измерениях, кроме трех, нет смысла описывать вращение как вращение вокруг оси, поскольку более чем одна ось объекта может оставаться неподвижной; вместо этого простые вращения описываются как происходящие в плоскости. В четырех или более измерениях комбинация двух или более вращений вокруг плоскости обычно не является вращением в одной плоскости.

Ось двумерного вращения

Дополнительная информация: Вращения в двух измерениях.

Двумерные вращения, в отличие от трехмерных, не имеют оси вращения, а имеют только точку, вокруг которой происходит вращение. Для линейных преобразований это эквивалентно утверждению, что в плоскости не существует направления, которое сохранялось бы неизменным при двумерном вращении, за исключением, конечно, тождественного.

Вопрос о существовании такого направления — это вопрос о существовании собственного вектора матрицы А, представляющей вращение. Каждое двумерное вращение вокруг начала координат на угол $\theta$ против часовой стрелки можно довольно просто представить следующей матрицей :

$A={\begin{bmatrix}\cos \theta &-\sin \theta \\\sin \theta &\cos \theta \end{bmatrix}}$

Стандартное определение собственных значений приводит к характеристическому уравнению

$\lambda ^{2}-2\lambda \cos \theta +1=0,$

который имеет

$\cos \theta \pm i\sin \theta$

как его собственные значения. Следовательно, реального собственного значения не существует всякий раз, когда $\cos \theta \neq \pm 1$, что означает, что ни один действительный вектор на плоскости не остается неизменным с помощью A .

Угол поворота и ось в 3 измерениях

Основная статья: Вращение вокруг фиксированной оси

Зная, что след является инвариантом, угол поворота $\alpha$ для правильной ортогональной матрицы вращения 3 × 3 $A$ находится по

$\alpha =\cos ^{-1}\left({\frac {A_{11}+A_{22}+A_{33}-1}{2}}\right)$

Используя главный арккосинус, эта формула дает угол поворота, удовлетворяющий $0\leq \alpha \leq 180^{\circ }$. Соответствующая ось вращения должна быть определена так, чтобы указывать в направлении, ограничивающем угол поворота не более 180 градусов. (Это всегда можно сделать, поскольку любой поворот более чем на 180 градусов вокруг оси $m$ всегда можно записать в виде вращения, имеющего $0\leq \alpha \leq 180^{\circ }$ если ось заменить на $n=-m$.)

Каждое правильное вращение $A$ в трехмерном пространстве имеет ось вращения, которая определяется так, что любой вектор $v$ который выровнен по оси вращения, не будет подвержен вращению. Соответственно, $Av=v$, и поэтому ось вращения соответствует собственному вектору матрицы вращения, связанному с собственным значением, равным 1. Пока угол поворота $\alpha$ не равно нулю (т. е. вращение не является единичным тензором), существует одно и только одно такое направление. Поскольку A имеет только действительные компоненты, существует по крайней мере одно действительное собственное значение, а оставшиеся два собственных значения должны быть комплексно сопряженными друг с другом (см. Собственные значения и собственные векторы#Собственные значения и характеристический полином ). Зная, что 1 является собственным значением, отсюда следует, что оставшиеся два собственных значения являются комплексно-сопряженными друг с другом, но это не означает, что они комплексные — они могут быть вещественными с двойной кратностью. В вырожденном случае угла поворота $\alpha =180^{\circ }$, оставшиеся два собственных значения равны −1. В вырожденном случае нулевого угла поворота матрица вращения равна единице, а все три собственных значения равны 1 (это единственный случай, когда ось вращения произвольна).

Для нахождения оси вращения спектральный анализ не требуется. Если $n$ обозначает единичный собственный вектор, совмещенный с осью вращения, и если $\alpha$ обозначает угол поворота, то можно показать, что $2\sin(\alpha )n=\{A_{32}-A_{23},A_{13}-A_{31},A_{21}-A_{12}\}$. Следовательно, затрат на анализ собственных значений можно избежать, просто нормализовав этот вектор, если он имеет ненулевую величину. С другой стороны, если этот вектор имеет нулевую величину, это означает, что $\sin(\alpha )=0$. Другими словами, этот вектор будет равен нулю тогда и только тогда, когда угол поворота равен 0 или 180 градусов, и ось вращения в этом случае может быть задана путем нормализации любого столбца $A+I$ имеет ненулевую величину.

Это обсуждение применимо к правильному вращению и, следовательно, $\det A=1$. Любая неправильная ортогональная матрица 3х3. $B$ может быть записано как $B=-A$, в котором $A$ является собственно ортогональным. То есть любая неправильная ортогональная матрица 3x3 может быть разложена как правильное вращение (из которого можно найти ось вращения, как описано выше) с последующей инверсией (умножением на -1). Отсюда следует, что ось вращения $A$ также является собственным вектором $B$ соответствующий собственному значению −1.

Плоскость вращения

Основная статья: Плоскость вращения

Точно так же, как каждое трехмерное вращение имеет ось вращения, каждое трехмерное вращение имеет плоскость, которая перпендикулярна оси вращения и остается неизменной при вращении. Вращение, ограниченное этой плоскостью, представляет собой обычное двумерное вращение.

Доказательство проводится аналогично предыдущему обсуждению. Во-первых, предположим, что все собственные значения матрицы трехмерного вращения A действительны. Это означает, что существует ортогональный базис, образованный соответствующими собственными векторами (которые обязательно ортогональны), по которому эффект матрицы вращения просто растягивает его. Если мы напишем А в этом базисе, то оно диагональное; но диагональная ортогональная матрица состоит только из +1 и -1 в диагональных элементах. Следовательно, перед нами не собственное вращение, а либо тождество, либо результат последовательности отражений.

Отсюда следует, что собственное вращение имеет некоторое комплексное собственное значение. Пусть v — соответствующий собственный вектор. Затем, как мы показали в предыдущей теме, ${\bar {v}}$ также является собственным вектором, и $v+{\bar {v}}$ и $i(v-{\bar {v}})$ таковы, что их скалярное произведение обращается в нуль:

$i(v^{\text{T}}+{\bar {v}}^{\text{T}})(v-{\bar {v}})=i(v^{\text{T}}v-{\bar {v}}^{\text{T}}{\bar {v}}+{\bar {v}}^{\text{T}}v-v^{\text{T}}{\bar {v}})=0$

потому что, поскольку ${\bar {v}}^{\text{T}}{\bar {v}}$ веществен, он равен своему комплексно-сопряженному $v^{\text{T}}v$, и ${\bar {v}}^{\text{T}}v$ и $v^{\text{T}}{\bar {v}}$ оба являются представлениями одного и того же скалярного произведения между $v$ и ${\bar {v}}$.

Это означает $v+{\bar {v}}$ и $i(v-{\bar {v}})$ являются ортогональными векторами. Кроме того, они оба являются действительными векторами по построению. Эти векторы охватывают то же подпространство, что и $v$ и ${\bar {v}}$, которое является инвариантным подпространством при применении A . Следовательно, они охватывают инвариантную плоскость.

Эта плоскость ортогональна инвариантной оси, которая соответствует оставшемуся собственному вектору A с собственным значением 1 из-за ортогональности собственных векторов A .

Вращение векторов

Вектор называется вращающимся, если он меняет свою ориентацию. Этот эффект обычно сопровождается только тогда, когда вектор скорости изменения имеет ненулевой компонент, перпендикулярный исходному вектору. В этом можно убедиться, рассмотрев вектор ${\vec {A}}$ который параметризуется некоторой переменной ${\textstyle t}$ для чего:

${d|{\vec {A}}|^{2} \over dt}={d({\vec {A}}\cdot {\vec {A}}) \over dt}\Rightarrow {d|{\vec {A}}| \over dt}={d{\vec {A}} \over dt}\cdot {\hat {A}}$

Что также дает соотношение скорости изменения единичного вектора, принимая ${\vec {A}}$, чтобы быть таким вектором: $${d{\hat {A}} \over dt}\cdot {\hat {A}}=0$$показывая это ${\textstyle {d{\hat {A}} \over dt}}$ вектор перпендикулярен вектору, ${\vec {A}}$.

От:

${d{\vec {A}} \over dt}={d(|{\vec {A}}|{\hat {A}}) \over dt}={d|{\vec {A}}| \over dt}{\hat {A}}+|{\vec {A}}|\left({d{\hat {A}} \over dt}\right)$,

поскольку первый член параллелен ${\vec {A}}$ и второго перпендикуляра к нему, можно в общем заключить, что параллельная и перпендикулярная составляющие скорости изменения вектора независимо влияют только на величину или ориентацию вектора соответственно. Следовательно, вращающийся вектор всегда имеет ненулевой перпендикулярный компонент вектора скорости изменения относительно самого вектора.

В высших измерениях

Смотрите также: Вращения в 4-мерном евклидовом пространстве.

По мере увеличения размеров количество векторов вращения увеличивается. В четырехмерном пространстве ( гиперобъеме ) вращения происходят вдоль осей x, y, z и w. Объект, повернутый по оси aw, пересекает различные объемы , где каждое пересечение равно отдельному объему под углом. Это уступает место новой оси вращения в 4D-гиперобъеме, где 3D-объект можно вращать перпендикулярно оси Z.

Физика

Скорость вращения определяется угловой частотой (рад/с), частотой ( оборотов за раз) или периодом (секунды, дни и т. д.). Скорость изменения угловой частоты – это угловое ускорение (рад/с ² ), вызванный крутящим моментом . Отношение крутящего момента к угловому ускорению определяется моментом инерции .

Вектор угловой скорости ( аксиальный вектор ) также описывает направление оси вращения. Аналогично, крутящий момент является аксиальным вектором.

Физика вращения вокруг фиксированной оси математически описывается с помощью ось-угол представления вращения . Согласно правилу правой руки , направление от наблюдателя связано с вращением по часовой стрелке, а направление к наблюдателю с вращением против часовой стрелки, как винт .

Круговое движение

См. Также: Круговое движение и Вращение вокруг фиксированной оси.

Движение слева, пример криволинейного перемещения, не может рассматриваться как вращение, поскольку не происходит изменения ориентации, тогда как правое движение можно рассматривать как вращение.

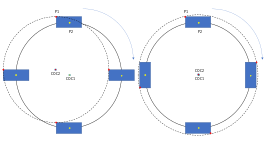
могут Объекты иметь периодические круговые траектории без изменения своей ориентации . Эти типы движения рассматриваются как круговое движение , а не как вращение, точнее, как криволинейное перемещение. Поскольку перемещение предполагает перемещение при твердых тел сохранении ориентации тела, в случае криволинейного перемещения все точки имеют одинаковую мгновенную скорость, тогда как относительное движение можно наблюдать только при движениях, связанных с вращением.

При вращении ориентация объекта меняется, и это изменение ориентации не зависит от наблюдателей, чьи системы отсчета имеют постоянную относительную ориентацию с течением времени. По теореме Эйлера любое изменение ориентации можно описать вращением вокруг оси, проходящей через выбранную точку отсчета. Следовательно, различие между вращением и круговым движением можно провести, потребовав для вращения мгновенную ось, линию, проходящую через мгновенный центр окружности и перпендикулярную плоскости движения . В примере, изображающем криволинейное перемещение, центр кругов движения лежит на прямой линии, но параллелен плоскости движения и, следовательно, не соответствует оси вращения. Напротив, вращающееся тело всегда будет иметь мгновенную ось нулевой скорости, перпендикулярную плоскости движения.

В более общем смысле, согласно теореме Часла , любое движение твердых тел можно рассматривать как комбинацию вращения и перемещения , называемую движением в общей плоскости. Простой пример чистого вращения рассматривается при вращении вокруг неподвижной оси .

Космологический принцип

законы физики В настоящее время считается, что инвариантны при любом фиксированном вращении . (Хотя кажется, что они меняются, если смотреть с вращающейся точки зрения: см. вращающуюся систему отсчета .)

В современной физической космологии космологический принцип — это представление о том, что распределение материи во Вселенной однородно и изотропно , если рассматривать его в достаточно большом масштабе, поскольку ожидается, что силы будут действовать равномерно во всей Вселенной и не будут иметь предпочтительного направления и должны , следовательно, не вызывают заметных нарушений в крупномасштабном структурировании в ходе эволюции поля материи, первоначально заложенного Большим взрывом.

В частности, для системы, которая ведет себя одинаково независимо от того, как она ориентирована в пространстве, ее лагранжиан инвариантен вращательно- . Согласно теореме Нётер , если действие ( интеграл по времени от ее лагранжиана) физической системы инвариантно относительно вращения, то угловой момент сохраняется .

Эйлеровы вращения

Основная статья: углы Эйлера

Эйлерово вращение Земли. Внутренний (зеленый), прецессия (синий) и нутация (красный)

Вращения Эйлера дают альтернативное описание вращения. Это композиция трех вращений, определяемая как движение, полученное путем изменения одного из углов Эйлера , оставляя два других постоянными. Эйлеровы вращения никогда не выражаются через внешнюю систему отсчета или через сопутствующую вращающуюся систему отсчета тела, а в смеси. Они представляют собой смешанную систему осей вращения, где первый угол перемещает линию узлов вокруг внешней оси z , второй - вокруг линии узлов , а третий - собственное вращение вокруг оси, закрепленной в движущемся теле.

Эти вращения называются прецессией , нутацией и собственным вращением .

Астрономия

Звездные следы , вызванные вращением Земли во время выдержки камеры длительной

Дополнительная информация: Период вращения и вращение Земли.

В астрономии вращение — часто наблюдаемое явление; оно включает в себя как вращение (автовращение), так и орбитальное вращение.

Вращаться

Звезды , планеты и подобные им тела могут вращаться вокруг своих осей. Скорость вращения планет Солнечной системы впервые была измерена путем отслеживания визуальных особенностей. Вращение звезды измеряется посредством доплеровского сдвига или путем отслеживания активных элементов поверхности. Примером являются солнечные пятна , которые вращаются вокруг Солнца с той же скоростью, что и внешние газы , составляющие Солнце.

При некоторых обстоятельствах вращающиеся тела могут синхронизировать свое вращение с орбитальным вращением вокруг более крупного тела. Этот эффект называется приливной блокировкой ; Луна привязана к Земле приливно-отливными силами.

Это вращение вызывает центробежное ускорение в системе отсчета Земли, которое немного противодействует эффекту гравитации, чем ближе к экватору . Гравитация Земли сочетает в себе оба массовых эффекта, так что объект на экваторе весит немного меньше, чем на полюсах. Другая причина заключается в том, что со временем Земля слегка деформируется в сплюснутый сфероид ; аналогичная экваториальная выпуклость развивается и у других планет.

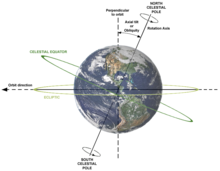
Другим следствием вращения планеты являются явления прецессии и нутации . Как и в случае с гироскопом , общий эффект представляет собой небольшое «раскачивание» движения оси планеты. В настоящее время наклон оси Земли к плоскости ее орбиты ( наклон эклиптики ) составляет 23,44 градуса, но этот угол меняется медленно (в течение тысяч лет). (См. также Прецессия равноденствий и Полярная звезда .)

Революция

Основная статья: Орбитальная революция

Хотя революция часто используется как синоним вращения , во многих областях, особенно в астрономии и смежных областях, революция , которую для ясности часто называют орбитальным вращением , используется, когда одно тело движется вокруг другого, тогда как вращение используется для обозначения движения вокруг тела. ось. Луны вращаются вокруг своих планет, планеты вращаются вокруг своих звезд (например, Земля вокруг Солнца); и звезды медленно вращаются вокруг своих галактических центров . Движение компонентов галактик сложное, но оно обычно включает в себя компонент вращения.

Ретроградное вращение

Основная статья: Ретроградное движение

Большинство планет Солнечной системы , включая Землю , вращаются в том же направлении, что и Солнце . Исключением являются Венера и Уран . Венеру можно рассматривать как медленно вращающуюся назад (или находящуюся «вверх ногами»). Уран вращается почти на боку относительно своей орбиты. Текущие предположения заключаются в том, что Уран вначале имел типичную прямую ориентацию, но в начале своей истории был сбит на бок сильным ударом. Карликовая планета Плутон (ранее считавшаяся планетой) аномальна по нескольким причинам, в том числе тем, что она еще и вращается на боку.

Динамика полета

Основная статья: Главные оси самолета

Главные оси вращения в пространстве

В динамике полета основные вращения, описанные выше углами Эйлера, известны как тангаж , крен и рыскание . Термин «вращение» также используется в авиации для обозначения подъема самолета вверх (нос поднимается вверх), особенно при начале набора высоты после взлета.

Преимущество основных вращений заключается в моделировании ряда физических систем, таких как подвесы и джойстики , поэтому они легко визуализируются и являются очень компактным способом хранения вращения. Но их сложно использовать в расчетах, поскольку даже простые операции, такие как объединение вращений, являются дорогостоящими и страдают от формы блокировки карданного подвеса , при которой углы не могут быть однозначно рассчитаны для определенных вращений.

Аттракционы

Многие аттракционы предусматривают ротацию. Колесо обозрения имеет горизонтальную центральную ось и параллельные оси для каждой гондолы, где вращение противоположно, под действием силы тяжести или механически. В результате в любой момент гондола ориентируется вертикально (не вращается), а просто перемещается. Кончик вектора перевода описывает круг. Карусель . обеспечивает вращение вокруг вертикальной оси Многие аттракционы предусматривают сочетание вращений вокруг нескольких осей. В Chair-O-Planes вращение вокруг вертикальной оси обеспечивается механически, а вращение вокруг горизонтальной оси происходит за счет центростремительной силы . В инверсиях американских горок вращение вокруг горизонтальной оси составляет один или несколько полных циклов, при этом инерция удерживает людей на своих местах.

Спорт

«Вращение» перенаправляется сюда. Чтобы узнать о других значениях, см. Вращение (значения) .

Вращение мяча или другого объекта, обычно называемое вращением , играет роль во многих видах спорта, включая верхнее и обратное вращение в теннисе , английском языке , следование и розыгрыш в бильярде и пуле , кривые шары в бейсболе , боулинг с вращением в крикете , виды спорта с летающими дисками , и т. д. Ракетки для настольного тенниса изготавливаются с различными характеристиками поверхности, что позволяет игроку придавать мячу большее или меньшее вращение.

Вращение игрока один или несколько раз вокруг вертикальной оси может называться вращением в фигурном катании , вращением (дубинки или исполнителя) в вращении палочки или на 360 , 540 , 720 и т.д. в сноуборде и т.п. игрок или исполнитель один или несколько раз вокруг горизонтальной оси может называться флипом , кувырком , сальто , хели и т. д. в гимнастике , катании на водных лыжах или многих других видах спорта, или полутора , два с половиной -половина , гейнер (начинание лицом от воды) и т. д. в прыжках в воду и т. д. Сочетание вертикального и горизонтального вращения (сальто назад на 360°) называется мёбиусом в прыжках на водных лыжах вольным стилем .

Вращение игрока вокруг вертикальной оси, обычно на 180–360 градусов, можно назвать вращением и использовать в качестве обманного маневра или маневра уклонения, а также в попытке сыграть, передать или получить мяч или шайбу и т. д. или дать игроку возможность видеть ворота или других игроков. Его часто можно увидеть в хоккее , баскетболе , футболе различных кодов, теннисе и т. д.

См. также

• Абсолютное вращение – вращение независимо от какой-либо внешней ссылки.
• Круговое движение
• Циклон – крупномасштабная вращающаяся воздушная масса.
• Мгновенный центр вращения - мгновенно неподвижная точка на произвольно движущемся твердом теле.
• Принцип Маха - умозрительная гипотеза о том, что физический закон связывает движение далеких звезд с местной инерциальной системой отсчета.
• Ориентация (геометрия)
• Точечное отражение
• Вращение – движение двух объектов, соприкасающихся друг с другом, без скольжения.
• Вращение (количество) - безразмерный скаляр, представляющий количество вращений.
• Вращение вокруг фиксированной оси
• Формализмы вращения в трех измерениях
• Вращающееся передвижение в живых системах.
• Верх – вращающаяся игрушка

Внешние ссылки

• «Вращение» , Математическая энциклопедия , EMS Press , 2001 [1994]
• Продукт вращений при разрезании узла . Cut-the-knot.org
• Когда треугольник равносторонний при разрезании узла. Cut-the-knot.org
• Поворот точек с использованием полярных координат , Howtoproperly.com
• «Вращение в двух измерениях» Серджио Ганнибала Мехиа по мотивам работы Роджера Гермундссона и «Понимание трехмерного вращения» Роджера Гермундссона, Демонстрационный проект Wolfram . демонстрации.wolfram.com
• Вращение, отражение и смена кадра: ортогональные тензоры в вычислительной инженерной механике , IOP Publishing